План урока

преподавателя – Мачалиной Натальи Ивановны.

по  учебной дисциплине – математика.

Дата проведения занятия: 16  декабря 2020 г.

Группа: №  М-20-12.

Время, отведенное на занятие: 90 минут.

Тема урока: обратные тригонометрические функции.

Тип урока:  изучения и первичного закрепления новых знаний.

Форма обучения:  классно-урочная.

Форма деятельности: фронтальная и индивидуальная.

Цель урока: знакомство с обратными тригонометрическими функциями; формирование знаний и умений в нахождении обратных тригонометрических функций.

Задачи  урока:

 

1.  Образовательные:

- дать определения обратным тригонометрическим функциям;

- рассмотреть основные  свойства обратных тригонометрических функций;

- показать способы вычисления обратных тригонометрических функций;

- обеспечить в ходе урока   обучение правильному применению основных свойств обратных тригонометрических функций и таблицы значений тригонометрических функций.

 

2.  Развивающие:

- способствовать развитию у обучающихся  умений анализировать, устанавливать связи, причины и следствия;

- предвидеть возможные ошибки и способы их устранения;

- способствовать повышению концентрации внимания, развитию у обучающихся памяти и речи.

 

3.  Воспитательные:

- способствовать развитию  интереса к предмету «Математика»;

- способствовать развитию самостоятельности мышления;

- способствовать формированию  нравственных качеств личности (уверенность в себе, целеустремленность).

Методы обучения: словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО); практические методы.

Оборудование: компьютер, проектор, раздаточный материал.

Дидактическая структура  урока	Содержание	Методическая структура урока			Признаки решения дидактических задач
		Методы обучения	Форма деятельности	Средства обучения
Организационный момент	- приветствие; - определение цели и задач урока.	словесные методы	фронтальная		Обучающиеся готовы к занятию
Актуализация знаний	Вопросы к группе: - какие функции вы уже знаете? - дайте определения тригонометрическим функциям; - синус какого угла равен ; ; ? - найдите значения ;; ; .	словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО)	фронтальная	компьютер, проектор, слайды с вопросами	Обучающиеся отвечают на вопросы
Сообщение нового материала	Дать определения функциям: - арксинус; - арккосинус; - арктангенс; - арккотангенс.   Показать примеры  нахождений значений обратных   тригонометрических функций.   Познакомить обучающихся с основными свойствами обратных тригонометрических функций.	словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО); практические методы.	фронтальная и индивидуальная	компьютер, проектор, слайды со свойствами обратных тригонометрических функций	Обучающиеся: - воспринимают материал; - находят значения обратных тригонометрических функций; - сравнивая решения  с образцами, самостоятельно обнаруживают ошибки и  корректируют решение.
Закрепление изученного материала	Самостоятельная работа обучающихся по теме урока	словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО); практические методы.	индивидуальная	раздаточный материал	Обучающиеся выполняют самостоятельную работу
Подведение итогов, рефлексия	Вопросы к группе: - какие функции вы сегодня изучили?   - в чем испытывали затруднения?   Педагог анализирует  и оценивает успешность выполнения поставленных задач.   Педагог просит обучающихся оценить урок с помощью карточек трёх цветов: «красная» - «отлично», «зелёная» - «хорошо», «синяя» - «удовлетворительно».	словесные методы	фронтальная, индивидуальная	карточки трёх  цветов	Обучающиеся отвечают на вопросы педагога  и оценивают урок
Домашнее задание	Выполнить дома следующие задания: - выучить определения обратных  тригонометрических функций и их свойства; - выполнить задания из учебника: №  126; № 127; № 128; № 129.	словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО).	фронтальная	компьютер, проектор, слайды с заданиями	Обучающиеся записывают домашнее задание

 

План - конспект

 

Обратные тригонометрические функции.

 

1.                Арксинус.

Определение.

 

Арксинусом числа α называется такое число из отрезка , синус которого равен α.

 

 

 

Упражнения с решениями.

 

Пример 1. Вычислите: а) ; б) .

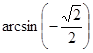Решение. а) Так как  и , то .

б) Так как  и , то .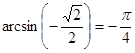

 

2. Арккосинус.

Определение.

 

Арккосинусом числа α называется такое число из отрезка , косинус которого равен α.

 

Упражнения с решениями.

 

Пример 2.  Вычислите: а) 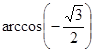; б) .

Решение. а) Так как  и , то .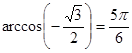

б) Так как  и , то .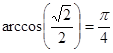

 

3. Арктангенс.

Определение.

 

 

 Арктангенсом числа α называется такое число из интервала , тангенс которого равен α.

 

 

Упражнения с решениями.

 

Пример 3. Вычислите: а) ; б) .

Решение. а) Так как  и , то .

б) Так как  и , то .

4. Арккотангенс.

Определение.

 

Арккотангенсом числа α называется такое число из интервала , котангенс которого равен α.

 

Упражнения с решениями.

 

Пример 4. Вычислите: а) ; б) .

Решение. а) Так как  и , то .

б) Так как  и , то .

 

 

5. Свойства обратных тригонометрических функций.

 

, если ;                                                      (1)

, если ;                                                               (2)

, если ;                                                              (3)

, если ;                                                            (4)

, если ;                                                               (5)

, если ;                                                              (6)

, если ;                                                                (7)

, где R.                                                                           (8)

, где R.                                                                        (9)

,гдеR.                                                                 (10)

 

 

 

Упражнения с решениями.

 

Пример 5. Вычислите:

а) ;

б) ;

в) ;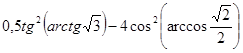

г) .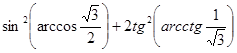

 

Решение а) Согласно тождествам (2) и (3) имеем:

.

 

 

б) Согласно тождествам (4), (5), (6) и (7) имеем:

.

 

 

в) Согласно формулам (3) и (8) имеем:

.

 

 

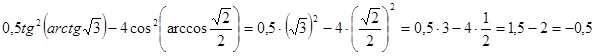г) Так как  и , то

 

 

 

 

 

 

 

 

 

 

 

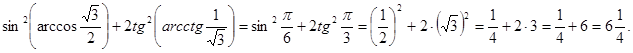
Самостоятельная работа

 

Вариант №1.

Вычислите:

а) ;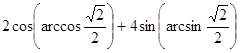

б) ;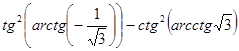

в) ;

г) .

 

 

Самостоятельная работа

 

 

Вариант №2.

Вычислите:

а) ;

б) ;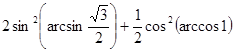

в) ;

г) .