"Математика и законы красоты"

УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ ЛИПЕЦКОЙ ОБЛАСТИ

ГОСУДАРСТВЕННОЕ ОБЛАСТНОЕ БЮДЖЕТНОЕ

ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»

Проект на тему

«Математика и законы красоты»

Липецк, 2021

Содержание

                                                    Введение

«Математика владеет не только

истиной, но и высшей красотой»

Бертран Рассел.

Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема. И именно красота является одним из связующих звеньев науки и искусства.

Математика – это не только стройная система законов, теорем, задач, но и уникальное средство познания красоты.

С давних пор человек стремится окружать себя красивыми вещами. Уже предметы обихода жителей древности демонстрируют стремление человека к красоте. На определенном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного?

 Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый – красоту в истине.

Красота скульптуры, красота храма, красота картины, симфонии,  поэмы  … Что между ними общего? Разве можно сравнивать красоту храма с красотой ноктюрна? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов – от цветка ромашки до обнаженного человеческого тела.

Существует актуальность темы  на сегодняшний день для людей многих профессий: для тех, кто стремится сделать мир гармоничнее и красивее.

Если мы  найдем формулу красоты, то разгадаем все её секреты, решив проблему отсутствия гармонии во многих вещах и явлениях современного общества.

Итак, объектом нашего исследования является: пропорциональная зависимость по принципу Золотого сечения в предметах окружающего мира.

Цель данной работы заключается в том, чтобы изучить математические законы красоты и их применение.

.    Глава I. Что такое Золотое сечение и как его найти

     "Формул красоты" уже известно немало.

 Из многих закономерностей, которыми издавна пользовался человек при создании гармонических произведений, существует одна, единственная и неповторимая, обладающая уникальными свойствами. Эту закономерность  называют по разному - "золотой", "божественной", "золотым сечением", "золотым числом". В ней - и мистическая тайна, и научный феномен. Речь идёт о разновидности геометрической пропорции, в которой осуществляется  деление отрезка на неравные части, при котором весь отрезок так относится к большей части , как сама большая часть относится к меньшей. (приложение 1)

(Отношение золотого сечения выражается числом 0,618.

Пропорция золотого сечения 1:0,618= 0,618:0,382.)

Глава II. Золотое сечение в окружающем мире

Архитектура и зодчество

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.(приложение 3)

 Велика роль пропорций в архитектуре.  Золотое сечение  замечено в таких постройках как: Парфенон, собор Василия Блаженного, Кижи и д.р.(приложение 4) 

Остановимся на одной из жемчужин древнерусской архитектуры - храме Василия Блаженного в Москве. Пропорции храма определяются восьмью членами ряда золотого сечения.

                Восприятие композиции. Искусство.

Ещё в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, как формат имеет картина – горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости . (приложение)

Живая природа

В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.          

                                   (приложение 5)

Все живое и все красивое – все подчиняется божественному закону, имя которому – «золотое сечение».

                    Пропорции человеческого тела

1)                Рассмотрим пропорции в строении тела человека. Начнем с лица.

 Лицо – это зеркало нашего культурного развития, личного опыта и генетических особенностей рода. И все же, почему об одном человеке мы можем сказать без особого энтузиазма "Да, он симпатичный", а лицо другого нас просто завораживает своей красотой? (приложение 5)

Говоря об идеальной внешности, можно привести следующие примеры золотого сечения:

Высота лица, деленная на ширину лица, равна 1,618;

Ширина рта, деленная на ширину носа, равна 1, 618;

Расстояние между зрачками, деленное на расстояние между бровями, равно 1,618.

И конечно же в наш век развития пластической хирургии, стоматологии и косметологии закон «золотого сечения» не могли упустить из вида.

Известный пластический хирург Стивен Марквардт 25 лет назад работал над тем, что бы сделать лица  более привлекательными. Он задался вопросом: "Что же такое привлекательность?" и стал детально изучать эту тему.  Целеустремленный хирург  вывел универсальные факторы описывающие красоту. И, взяв за основу труды Пифагора, Леонардо да Винчи и немецкого профессора Цейзинга, соединил все знания о "золотом сечении" и вывел формулу идеального лица. Создал маску красоты..(приложение).

Где же  ещё можно заметить Золотое сечение? (приложение).

Деление тела линией талии- важнейший показатель золотого сечения.

Пропорции золотого сечения проявляются и в отношении других частей тела- длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Таким образом, пропорции различных частей тела составляют число очень близкое к злотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то тело человека считается идеально сложенным.

Математика и искусство

"С давних пор человек стремится окружать себя красивыми вещами. Уже предметы обихода жителей древности, которые, казалось бы, преследовали чисто утилитарную цель - служить хранилищем воды, оружием на охоте и т.д., демонстрируют стремление человека к красоте. На определенном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного? Уже в Древней Греции изучение сущности красоты, прекрасного, сформировалось в самостоятельную ветвь науки - эстетику, которая у античных философов была неотделима от космологии. Тогда же родилось представление о том, что основой прекрасного является гармония.

Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый - красоту в истине.

Красота скульптуры, красота храма, красота картины, симфонии, поэмы... Что между ними общего? Разве можно сравнивать красоту храма с красотой ноктюрна? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов - от цветка ромашки до красоты обнаженного человеческого тела?.....".

Золотое сечение или «божественное деление» - это такое деление целого на две неравные части, при котором большая часть AC так относится к целому AB, как меньшая BC к большей AC.

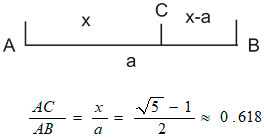
Отношения частей человеческого тела связывались с формулой золотого сечения. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т.д.

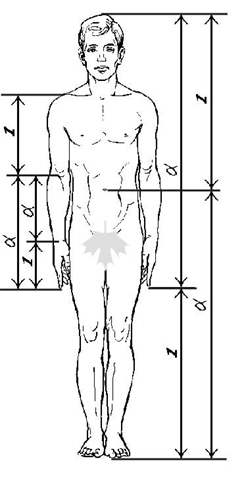
Пропорции “золотого сечения” создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения”. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. "Золотая пропорция" - это понятие математическое и ее изучение - это прежде всего задача науки. Но она же является критерием гармонии и красоты, а это уже категория искусства и эстетики.

Сам термин “золотое сечение” принадлежит Леонардо да Винчи. С тех пор многие шедевры искусства, архитектуры и музыки выполняются при неукоснительном соблюдении золотой пропорции. В геометрии существуют различные способы построения золотой пропорции, причем характерно, что для построения достаточно взять самые простые геометрические фигуры – квадрат или прямоугольный треугольник с соотношением катетов 1:2. Золотое сечение можно увидеть и в пентаграмме - так называли греки звездчатый многоугольник. Он служит символом Пифагорейского союза. Пентаграмма также содержит золотые треугольники – остроугольные с углами 36°, 72°, 72°. Интересен еще один замечательный треугольник, в котором проявляется золотая пропорция. В этом треугольнике углы равны 90°, 54° и 36°, а их отношение составляет 5:3:2.

Математика и литература

«Математика и литература…» Это тема возникла не случайно.

То, что математики являются не только тонкими ценителями изящной словесности, но и сами зачастую выступают маститыми литераторами, общеизвестно. Достаточно вспомнить профессора математики Оксфордского университета Чарльза Латуиджа Джонсона, который под псевдонимом Льюиса Кэрролла написал знаменитую сказку «Алиса в стране чудес». Говорят, английская королева, любившая «Алису» и попросившая доставить ей все произведения сказочника, была удивлена и расстроена, увидев его многочисленные сочинения по математической логике. Можно вспомнить и профессора математики Кембриджского университета Бертрана Рассела (1872-1970), начинавшего свою научную карьеру с фундаментального трехмерного труда по математической логике и закончившего Нобелевской премией по литературе (1950). Можно вспомнить скромного русского учителя математики Александра Солженицына, ставшего не только гордостью современной русской литературы, но и совестью современной России.

Но то, что строгие математические законы часто определяют структуру всего литературного произведения, подчас вызывает удивление даже у профессиональных филологов. Что понимает литература под каждодневными монологами и диалогами? Разумеется, законы формы. Но форма - это порядок, а порядок - это математика. Значит, чем строже литература следует законам формы, тем ярче в ней должны проявляться и законы математики.

Александр Сергеевич Пушкин – высочайшая вершина русской литературы. Но величайшие вершины национальных литератур определяют и главный вектор развития мировой литературы.

Нас интересует вопрос: определяют ли и если определяют, то в какой степени законы симметрии гармонию пушкинского стиха? Ибо с кого же начинать анализ симметрийных законов поэзии, как не с русского гения Пушкина?!

Мы остановимся только на малых поэтических формах в творческом наследии Пушкина. Если такие грандиозные памятники, как «Евгений Онегин», создаются годами, то стихотворение, как правило, пишется под влиянием минут. Стихотворение отражает состояние души поэта «здесь и сейчас», стихотворение «приходит» к поэту, и он едва успевает записать его на бумаге. Поэтому симметрийные законы формы в стихотворении возникают скорее на подсознательном уровне. Тем более интересно знать, насколько сильно или слабо эти законы вторгаются в творчество автора.

Золотое сечение в композиции стихотворения проявляется как наличие главного момента стихотворения (кульминации, смыслового перелома, главной мысли или их сочетаний) в строке, приходящейся на точку деления общего числа строк стихотворения в золотой пропорции. Часто национальная кульминация стихотворения является и его главной мыслью, а главная мысль совпадает со смысловым переломом стихотворений, т.е. часто различные функции золотого сечения в стихотворении слиты воедино.

При выяснении роли структур зеркальной симметрии и золотого сечения в поэзии Пушкина были изучены стихотворения русского гения за период его творческой биографии с 1813 по 1837 год включительно. Почти все они созданы одновременно, под влиянием какого-либо яркого впечатления, и потому является хорошим материалом для обнаружения корреляции гармонических структур с состоянием души поэта.

Но может быть, все эти удивительные примеру из области математики справедливы только для малых художественных форм? Тогда остановимся на величайшем романе в прозе.

«Война и мир» Льва Толстого - грандиозный памятник русской и мировой литературы. В произведение изображены широчайшие эпические картины войны русских и французов 1812 года и тончайшие нити переживаний, связующие внутренний мир героев романа. Статьи монографии о «Войне и мире» в сотни раз переросли по объему четыре тома самого произведения. И тем не менее…

Никто не замечал, что в самом заглавии романа – «Война и мир» - закодирован закон золотого сечения. В самом деле, название романа построена на первых четырех членах ряда Фибоначчи 1, 2, 3, 5. Один союз, два существительных, три слова. Пять букв в первом ключевом. Отношение ключевых слов 5:3=1,666… есть первое рациональное приближение коэффициента золотого сечения.

Золотые пропорции «Войны и мира» родились на подсознательном уровне, значит, Толстой был в состояние охватить внутренним взором весь роман целиком, держать в голове одномоментно всю колоссальную художественную форму!

Глава III. Применение законов математики как законов красоты в окружающей нас жизни

§ 1. Математика в мире растений.

Мир растений - величайшее чудо природы, царство красоты и наше целительное богатство. Изучением лекарственных растений занимается наука фитотерапия. Конечно, в этой науке математика играет не последнюю роль. О том, что и здесь применяется математика, мы можем найти сколь угодно много подтверждений. Симметрия листьев, красота цветов, палитра природных окрасов, пропорции стройных деревьев – всё подчинено закону симметричности, пропорциональности и целесообразности.

§ 2. Математика в жизни животных и насекомых.

Мир животных и насекомых - богатый и разнообразный мир живых существ. Этот мир, скажете вы, изучает раздел биологии - зоология. Но позвольте Вам всем возразить! Ведь и здесь не обойтись без математики. Вы когда-нибудь обращали внимание на симметрию крыльев бабочки, на причудливые узоры змеиной кожи, а какие есть красивые по цвету морские и аквариумные рыбки, ведь мы смотрим на них как завороженные. Да таких примеров можно приводить и приводить.

Вот, к примеру, пчёлы - удивительное творение природы. Они маленькие экономисты. Пчелиные соты представляют собой пространственный паркет (шестигранные призмы), поскольку заполняют пространство так, что не остаётся просвета.

Это математический шедевр из воска. А пауки умудряются плести свои паутины, соблюдая строгие пропорции. Как это возможно, ведь пчёлы и пауки не знают высшей математики?

§ 4. Математика и культура.

Нам стало интересно, а какое отношение имеет математика к культуре: ведь это и памятники архитектуры, прекрасные скульптуры и, в конце концов, это и живопись. Неужели и здесь мы можем наблюдать «незримое» влияние математики на культуру?! А начать решили с удивительных архитектурных памятников.

Даже сейчас, когда он стоит на развалинах, Парфенон в Афинах - это одно из самых знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой математики.

Фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза. А это соотношение в математике принято считать «золотой пропорцией».

Золотое соотношение мы можем увидеть и в пирамиде Хеопса, и в здании собора Парижской Богоматери, и в храме Василия Блаженного на Красной площади.

Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображённого человека делится пупочной линией в золотом сечении (талия делит совершенное человеческое тело в отношении золотого сечения примерно )

Скульпторы утверждают, что пропорции мужчин ближе к золотому сечению, нежели пропорции женщин (однако, женщина в обуви на каблуках может оказаться ближе к золотым пропорциям).

Ещё в эпоху Возрождения художники открыли, что любая картина имеет определённые точки, невольно приковывающие внимание, так называемые зрительные центры. Таких точек всего 4, они делят величину изображения по горизонтали и вертикали в золотом сечении. Данное открытие у художников того времени получило название «Золотое сечение» картины.

Переходя к примерам в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.

Портрет Моны Лизы привлекает нас тем, что композиция рисунка построена на «золотых треугольниках».

Математика и хореография

Казалось бы, что может быть общего между такими разными дисциплинами, как танцы и математика?

Танец – это искусство, выражение эмоций с помощью пластических движений тела. Тут мы понимаем, что танец – это тот перекрёсток, где математика сталкивается с искусством. Ведь движение – это изменение плоскости, при котором сохраняются размеры и форма объектов. Примерами движений служат симметрия и параллельный перенос. Такие геометрические движения можно найти во многих танцевальных постановках, особенно если танец построен на синхронном выполнении движений.

Кроме того, танцоры невольно внедряют математику в искусство с помощью пространственного мышления. Кстати, доказано, что танцы благотворно влияют не только на физическую форму, но и на умственные способности ребёнка, пространственное воображение.

В каждом танце важен счёт, а считать мы учимся, конечно, только с помощью математики.

Танцоры «выстраивают» своим телом разнообразные фигуры, и это тоже особый случай. Тут не обойтись без геометрии! Расчёт траектории движения – очень сложная наука, связанная с математическими расчётами, физическими формулами и углами.

Ещё один факт, подтверждающий связь танца и математики, – это использование общих терминов: линии, диагонали, колонны, в рисунке танца они могут располагаться параллельно или перпендикулярно.

Конечно же, в каждом танце есть симметрия. Ну, или асимметрия.

Поговорим немного о том, как эту мистическую связь танца и математики применяют на практике.

Перед вами Уильям Форсайт, всемирно известный хореограф. Однажды, придумывая новую хореографическую связку, он заметил некую математическую особенность в своих движениях…

Он стал рисовать в воздухе воображаемые фигуры, а затем протаскивать свои конечности через эту сложную и невидимую геометрию. Позднее ему предложили использовать компьютерную анимацию, наложенную на видеозапись его движений, чтобы сделать эту геометрию видимой. И Уильям создал мультимедийную работу, названную «Технологии импровизации». С тех пор он реально использует её в обучении новых участников своей танцевальной компании.

Вот как сам Ульям говорит об этом: «Я анализировал те знания о пространстве и собственном теле, которое танцоры балета вынесли из своей интенсивной подготовки и выяснил, что их обучали работать с линиями и формами в пространстве. Таким образом, я начал представлять линии в пространстве, которые могли бы изгибаться, идти волнами или деформироваться другими способами. Двигаясь от точки к линии, затем к плоскости, затем к объёму, я мог визуализировать геометрическое пространство. Неограниченное количество позиций и движений можно создавать, используя различные последовательности только из сгибаний и разгибаний. Исходя из этого, мы начали составлять каталог того, что тело может делать…»

И этот способ творчества в хореографии весьма успешен: балет Форсайта знают по всему миру.

«Мы хотим увидеть эту самую геометрию на практике!» – скажете вы. Что ж… Желание зрителя – закон!

Таким образом, хотя чтобы заниматься танцами и не обязательно быть Нобелевским лауреатом по математике, но присутствие её, зримое или незримое, мы ощущаем в любом танце, независимо от стиля или исполнения

Математика и философия

Некоторые математики придерживаются мнения, что достижения их науки можно с бо́льшим правом называть не изобретением, а открытием, которое, по своему смыслу, ближе к нахождению:

«Вы не найдете исследователя, поэта, художника, музыканта, который не скажет, что нашел свое открытие, стихотворение или картину готовыми — что они пришли извне, а не были созданы им осознанно изнутри». — Уильям Кингстон Клиффорд, из лекции в Королевском институте на тему «Некоторые условия развития мышления

Кроме того, математики, придерживающиеся подобной точки зрения, считают, что подробные и точные результаты математики можно справедливо считать истинными вне зависимости от устройства вселенной, в которой мы живём. Например, они утверждают, что теория натуральных чисел обоснована таким образом, что принципиально не требует конкретного контекста рассмотрения. Наиболее радикальные из них приписывают математической красоте абсолютную истинность, тем самым тяготея к мистицизму.

Пифагорейцы верили в буквальную реальность чисел. Поэтому открытие иррациональных чисел стало тем более для них удивительным, поскольку возможность отношения двух натуральных чисел воспринималось ими как свидетельство несовершенства природы и было невыразимым — алогос (пифагорейское мировоззрение ничего не говорило о пределах бесконечных последовательностей отношения натуральных чисел). С современной точки зрения такой мистический подход, предполагавший единство и нераздельность чисел и геометрических объектов, можно назвать нумерологией.

В философии Платона существовали два мира: мир вещей, в котором мы живём, и мир идей, которые необходимы для существования реального мира. В мир идей входили также математические идеи.

Венгерский математик Пал Эрдёш  верил в существование воображаемой книги, в которой бог записал все самые прекрасные математические доказательства. И когда Эрдёш хотел выразить восхищение доказательством, он восклицал: «О, это из Книги!»

Французский философ XX века Ален Бадью  утверждает, что онтология по своей природе математична, так как математика может помыслить множество как таковое, а бытие есть непостоянная множественность.

Очень часто философы-натуралисты и другие учёные, широко пользующиеся математическим методом, делали безосновательный вывод относительно связи красоты с истиной, которые впоследствии оказываются ошибочными. Например, на одном этапе своей жизни Иоганн Кеплер считал, что пропорции орбит известных в его время планет Солнечной системы были установлены Богом в соответствии с концентрическим расположением пяти платоновских тел таким образом, что каждая из орбит одновременно была расположена на сфере описанной  около одного многогранника и вписанной  в следующий

Математика в живой и неживой природе.

Ещё Гете подчёркивал тенденцию природы к спиральности. Паук плетёт паутину спиралеобразно. Спирально закручивается смерч. Испуганные стада животных разбегается по спирали, а косяки рыб как бы мелькают мимо сети тоже по спирали. Молекула ДНК закручена двойной спиралью. Спираль мы можем увидеть в расположении семян подсолнечника, в шишках сосны, кедра ананасах, кактусах и т.д. Спираль создает не только красоту и порядок, но и модель бытия.

Снежинки: ярче примера очаровательной красоты и порядка в природе вы не найдете. Изучением снежинок занимался знаменитый Рене Декарт. А вообще-то, снежинки - это звёздчатые многоугольники. Они очаровательны ещё и потому, что они симметричны. А симметрия, как сказал Г. Вейль «Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство».

Проанализировав приложение математики в окружающей нас жизни, хочется заметить, что красота помогает с радостью воспринимать окружающий мир, а математика даёт возможность открывать всё новые и новые слагаемые красоты. Так и хочется сказать словами поэта

Все в мире связано в единое начало:

В движенье волн – шекспировский сонет,

В симметрии цветка – основы мирозданья,

А в пенье птиц - симфония планет.

У. Блейк

Изучив весь представленный вам материал, мы поняли, что о математике можно говорить вечно. Наверное, поэтому и символ вечности «∞» (бесконечность) мог появиться только с развитием этой науки «Математика». Мы решили перейти к практической части исследования и для начала провели небольшой социологический опрос, который должен нам помочь подтвердить или опровергнуть выдвинутую ранее гипотезу: если математика второстепенная наука, то можно утверждать, что без математических законов красоты можно обойтись; если же нет, то без знания математики вся современная жизнь невозможна.

Заключение

Таким образом, на основании изученной литературы и анализа интернет источников , мы можем сделать вывод о том, что без знания математических законов красоты вся современная жизнь невозможна. Например, у нас не было бы хороших домов с красивыми изящными линиями, т. к. строители должны уметь измерять, считать, сооружать. Наша одежда была бы грубой, т. к. её нужно хорошо, красиво скроить. Не было бы ни прекрасно спланированных парковых зон, никакой лёгкой промышленности и тысячи других вещей, составляющих часть нашей цивилизации.

В данной работе я выяснил, математика - часть мира, напрямую связанная с категорией красоты, которая создаётся по математическим формулам; часть мира, в котором мы живём.

Поэтому я могу с полной и абсолютной уверенностью воскликнуть:

Математика - это красота.!

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. А.Азевич “Двадцать уроков гармонии”. – М., “Школа-Пресс”, 1998.

2. Н.Васютинский “Золотая пропорция”. – М.,”Молодая гвардия”, 1990.

3. Д.Пидоу “Геометрия и искусство”. – М., “Мир”, 1989.

4. Энциклопедический словарь юного математика. – М., 1989.

5. А.В.Волошинов «Математика и искусство», Просвещение, 2000