Мир объёмных геометрических фигур

 Муниципальное казенное общеобразовательное учреждение

Крутовская основная школа

Серафимовичского района

Волгоградской области

ИсследовательскИЙ ПрОЕКТ

«МИР ОБЪЁМНЫХ ГЕОМЕТРИЧЕСКИХ ФИГУР»

Выполнил проект:

ученик 6 класса

МКОУ Крутовской  ОШ,

Глазунов Аристарх Евгеньевич

Руководитель:

учитель математики и информатики

МКОУ Крутовской ОШ,

Урасова Наталья Николаевна

х. Крутовский

2024-2025 учебный год

Содержание:

Введение.

I. Пространственные (объёмные) геометрические фигуры

1.1. Классификация пространственных (объёмных)

геометрических фигур

1.2. Составные элементы пространственных (объёмных) геометрических фигур

II. Пространственные (объёмные) геометрические фигуры в окружающем мире.

2.1. Пространственные (объёмные) геометрические фигуры в макромире.

2.2. Пространственные (объёмные) геометрические фигуры в микромире.

III. Изготовление коллекции моделей, изученных объёмных геометрических фигур в виде развёрток.

Заключение

Список литературы

Приложение 1

Приложение 2

Приложение 3

Введение

Посмотрите вокруг - как разнообразен наш мир, какие разные предметы нас окружают. В нашем мире много необычного и прекрасного. Нас окружают предметы, формы которых нас удивляют. Таковыми, например, являются геометрические фигуры. Эти фигуры обладают и красотой, и совершенностью форм, и притягательностью.  

Наши дома, и египетские пирамиды, и кубики, которыми играют дети, и объекты архитектуры и дизайна, и предметы обихода состоят из знакомых нам геометрических фигур.

Они встречаются в природе в виде кристаллов, и в виде вирусов. Архитекторы, строители и дизайнеры воплощают свои оригинальные идеи, используя эти фигуры. И можно заметить, что все это – плоские и объемные геометрические фигуры.

Целью данной работы является изучение и описание части пространственных (объёмных) геометрических фигур, способы их определения и применения, а также сконструировать коллекцию, изученных пространственных фигур.

Задачи работы:

1.        Познакомиться с многообразием пространственных (объёмных) геометрических фигур.

2.        Изучить виды объёмных геометрических фигур.

3.        Показать связь полученной информации с окружающим миром.

4.        Изготовить коллекцию моделей, изученных пространственных геометрических фигур в виде развёрток.

Актуальность проекта:

В течение многих веков математики проявляли интерес к пространственным (объемным) геометрическим фигурам. Интерес к ним обусловлен не только их красотой и оригинальностью, но и большой практической ценностью.

Участвуя в данном проекте, попадаешь в удивительный мир этих фигур. Узнаешь много нового об их видах и свойствах.

Таким образом, объектом нашего исследования будут пространственные геометрические фигуры, окружающие нас. А предметом исследования станут многогранники и тела вращения.

Методы исследования:

- теоретический: библиографический анализ литературы и материалов сети Internet;

- эмпирический: анализ полученных данных и изготовление моделей многогранников.

I. Пространственные (объёмные) геометрические фигуры

Наш мир представляет собой трехмерное пространство, в котором

фигуры имеют объем. Объемные фигуры обладают дополнительными

свойствами по сравнению с плоскими. Эта работа поможет нам разобраться,

какими свойствами обладают объемные тела.

1.1. Классификация пространственных (объёмных)

геометрических фигур

По форме пространственные геометрические (объёмные) фигуры делятся

на многогранники и тела вращения.

         Многогранники можно условно разделить на:

1.     Правильные многогранники (Платоновы тела).

2.     Пирамиды.

3.     Призмы.

         А тела вращения делятся на:

                        1. Цилиндр.

                        2. Конус.

                        3. Шар и сфера.

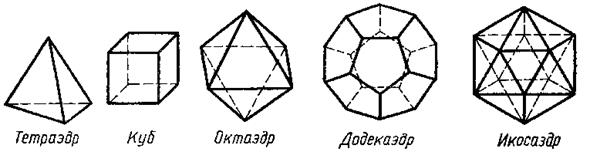         Оказывается, что правильных многогранников ровно пять - ни больше ни меньше. (рис.1). Ведь для того, чтобы получить какой-нибудь правильный многогранник, в каждой вершине, согласно его определению, должно сходиться одинаковое количество граней, каждая из которых является правильным многоугольником.

рис.1

Пирамида — это многогранник, который формируется, когда несколько треугольников, сходящихся в одной точке (вершине), соединяются с многоугольником на плоскости (основанием). Эта уникальная структура делает пирамиду одним из наиболее интересных объектов в геометрии (рис. 2).

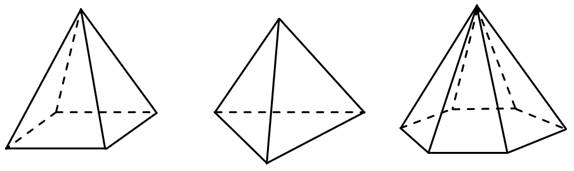
рис. 2

Призма — это многогранник, две грани которого представляют собой равные многоугольники, расположенные в параллельных плоскостях. Все рёбра, не лежащие в этих плоскостях, параллельны между собой (рис. 3).

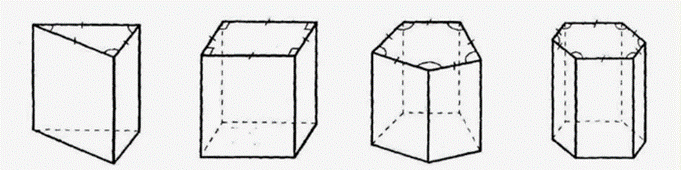
рис. 3

Цилиндр - это объёмная фигура, получена вращением прямоугольника вокруг оси, проходящей через центр прямоугольника. Цилиндр имеет два круга в основаниях и образующую (то, что соединяет основания) (рис. 4). 

Конус – это объёмная фигура получена путём вращения прямоугольного треугольника вокруг одного из своих катетов (рис. 4). 

Шар/сфера. Шар (заполненный внутри) — это геометрическое тело, ограниченное поверхностью, все точки которой отстоят на равном расстоянии от центра. Сфера (пустая внутри) — поверхность, образованная вращением контура (рис. 4). 

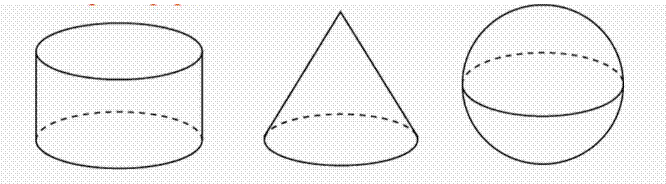(рис. 4)

Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.

Древнегреческий ученый Архимед обобщил понятие правильного многогранника и открыл новые математические объекты – полуправильные многогранники.

Нами были изучены только некоторые из них. Архимедовы тела получаются из Платоновых тел в результате их усечения.

Так могут быть получены пять архимедовых тел: усечённый тетраэдр, усечённый гексаэдр (куб), усечённый октаэдр (рис. 5).

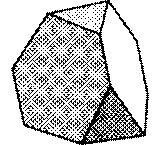
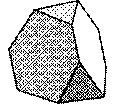
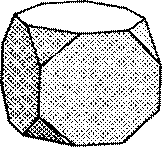
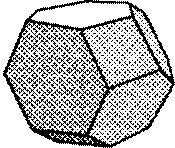
рис. 5

1.2. Составные элементы пространственных (объёмных) геометрических фигур

Пространственные (объёмные) геометрические фигуры из части многогранников имеют три неотъемлемых компонента:

- грань (поверхность многоугольника),

- вершина (углы, образовавшиеся в местах соединения граней),

- ребро (сторона фигуры или отрезок, образованный в месте стыка двух граней).

В стереометрии особое место занимают геометрические фигуры с абсолютно равными между собой гранями, в вершинах которых соединяется одинаковое количество рёбер. Эти тела получили название Платоновы тела, или правильные многогранники.

Названия правильных многогранников пришли из Древней Греции, в них указывается число граней:

 Боковые грани любой пирамиды представлены обязательно треугольниками, но в основании может быть как треугольник, так и четырёхугольник, и пятиугольник, и так до бесконечности. При этом название пирамиды будет соответствовать многоугольнику в основании.

Геометрическое тело, которое имеет обязательно две совершенно одинаковые грани в основании, лежащие в параллельных плоскостях, и различное число боковых граней в виде прямоугольников носит название призма. В свою очередь, призма имеет несколько разновидностей, в зависимости от вида многоугольников, лежащих в основаниях призмы.

Тела вращения — геометрические тела, которые представляют собой поверхность вращения.

II. Пространственные (объёмные) геометрические фигуры в окружающем мире

Стоит только внимательно осмотреться, и мы сразу обнаружим вокруг нас всевозможные пространственные геометрические фигуры. Оказывается, их очень много. Просто мы их раньше не замечали.

2.1. Пространственные (объёмные) геометрические фигуры в макромире

Многогранники в архитектуре. Архитектурные шедевры находятся в разных уголках земного шара. Людские желания воплощаются в форме необыкновенных зданий и сооружений (Приложение № 1).

Многогранники в искусстве. Леонардо да Винчи, Сальвадор Дали,

Альбрехт Дюрер, Мориц Корнилис Эшер - с работами этих мастеров можно ознакомиться в нашей работе (Приложении № 2).

Титан Возрождения, живописец, скульптор, ученый и изобретатель Леонардо да Винчи (1452-1519) — символ неразрывности искусства и науки. Закономерен его интерес к таким прекрасным, высоко симметричным объектам, как выпуклые многогранники (Приложение № 2).

Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471- 1528), в известной гравюре «Меланхолия» на переднем плане изобразил многогранник (Приложение № 2).

Голландский художник Мориц Корнилис Эшер (1898-1972) создал уникальные и очаровательные работы (Приложение № 2).

Правильные геометрические тела - многогранники - имели особое очарование для Эшера. Во многих его работах многогранники являются главной фигурой, и часто они встречаются в качестве вспомогательных элементов.

На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники полупрозрачные, и сквозь любой из них можно увидеть остальные (Приложение № 2).

Очень интересная работа Эшера - гравюра "Звезды" (Приложение № 2), на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, наверное, она не была бы столь исключительна. Но он по какой-то причине, поместил внутрь центральной фигуры хамелеонов, обеспечив ее незаурядность и уникальность.

На картине великого художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного  додекаэдра. (Приложение № 2). Красота этой картины не требует комментариев.

2.2. Пространственные (объёмные) геометрические фигуры в микромире

  В микромире многогранники встречаются в виде кристаллов, вирусов и бактерий - простейших организмов.

Кристаллы. Мир кристаллов - красивый, разнообразный, не менее загадочный, чем мир живой природы. В естественной среде правильные многогранники можно встретить в виде кристаллов (минералов).

Форму тетраэдра передает  сернокислый натрий. (Приложение № 3).

 Алмаз отчетливо передает форму октаэдра. (Приложение № 3)

Куб - монокристалл объединяет в себе кристаллы поваренной соли. (Приложение № 3).

Кристалл пирита имеет форму додекаэдра. Размеры кристаллов пирита достигают нескольких сантиметров. (Приложение № 3).

Бор – имеет форму икосаэдра (Приложение № 3).

Вирусы и бактерии. Исключительностью икосаэдра вирусы воспользовались не случайно. Тут все дело в экономии — экономии генетической информации. Вот так «решают» вирусы сложнейшую задачу: найти тело наименьшей поверхности при заданном объеме, и притом, состоящее из одинаковых и тоже простейших фигур.  

Бактериофаги (греч. phagos — пожиратель; буквально — пожиратели бактерий) - бактериальные вирусы, вызывающие разрушение бактерий и других микроорганизмов также имеют форму икосаэдра (Приложение № 3).

Одноклеточные организмы. Икосаэдр точно передает форму одноклеточных организмов. Из многогранников именно он имеет наибольший объём и наименьшую площадь поверхности. Это геометрическое свойство помогает морскому микроорганизму феодарии преодолевать давление воды (Приложение №3).

III. Изготовление коллекции объёмных геометрических фигур в виде развёрток

Раздел математики, который изучает фигуры в пространстве называется стереометрия. Существует мнение: изучение стереометрии затруднено тем, что многим людям мешает недостаточно развитое пространственное воображение.

На самом деле, это не совсем так, и способность представлять пространственные тела, мысленно перемещать их и трансформировать развита практически у любого человека, поскольку живет он в трехмерном пространстве.  

Если поверхность многогранника разрезать по некоторым рёбрам, а затем развернуть её на плоскости, то получится фигура, которую называют развёрткой многогранника.

Изучая развертки и склеивая из них модели многогранников, у Вас появятся навыки преобразования плоских форм в объемные.

Затем развивается еще более тонкая способность – раскладывать объемные формы на простые плоские. То есть, увидев предмет в реальном мире, Вы можете создать его развертку из бумаги, и, склеив, получить модель-копию любого объемного предмета.

Процесс создания пространственных геометрических фигур из бумаги настолько нас увлек, что мы создали свою небольшую коллекцию.

 ЗАКЛЮЧЕНИЕ

Итак, объёмные геометрические фигуры присутствуют в нашей жизни буквально во всём, и мы настолько к ним привыкли, что порой не замечаем этого. Благодаря этим фигурам в нашей жизни, и в искусстве, и в архитектуре и природе, нам открываются не только удивительные свойства геометрических фигур, но и пути познания гармонии и красоты.

Исследовательская работа была интересной и разнообразной, мы прикоснулись к удивительному миру красоты, совершенства, гармонии, узнали имена учёных, художников, которые посвятили этому миру свои труды, являющиеся шедеврами науки и искусства. Ещё раз убедились, что истоки математики – в природе, окружающей нас.

В рамках работы была изучена литература по теме, выявлены особенности и составные элементы пространственных геометрических фигур, изготовлены чертежи, развёртки, модели многогранников и составлена коллекция объёмных геометрических фигур в виде анимированной книги.  

Цель нашей работы достигнута, ведь мы не только познакомились с очередным математическим разделом, но и увлеклись миром объемных геометрических фигур.

В будущем наша анимированная книга будет пополнятся новыми объёмными моделями.

 СПИСОК ЛИТЕРАТУРЫ

1. Энциклопедия для детей. Т. 11. Математика. – М: Аванта плюс, 2002.

2. Энциклопедия для детей. Я познаю мир. Математика. – М: Издательство АСТ, 1999.

3. Ворошилов А.В. Математика и искусство. - М. просвещение, 1992. – 352

4. Рыбников К.А. История математики: Учебник. - М.: Изд-во МГУ, 1994. - 495

5. Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Часть 3 – М: Баласс,1988.

6. Шарыгин И. Ф., Ерганжиева Л.Н. Наглядная геометрия. Учебное пособие для V – VI классов. – М: Мирос 2024.

7. https://multiurok.ru/blog/mnoghoghrannikivprirodie.html?ysclid=m8ct49919r4008

8.  https://zhurnalpedagog.ru/servisy/publik/publ?id=17620  

9.  https://mnogogranniki.ru/estestvennye-mnogogranniki-chast-2.html?ysclid=m8ct371w1d217119422

Приложение 1

Многогранники в архитектуре

  Александрийский маяк                                                    Храм Артемиды Эфесской

        Спасская башня                                             Дворец мира и согласия» в Астане

     Казанского Кремля

     Гостиничные номера в                                   Национальная библиотека в Минске

        Краснодарском крае                 

                                                                                                                                         Приложение 2

                                                        Многогранники в искусстве

Иллюстрации Леонардо да Винчи для книги

«Божественная пропорция»

                     Мауриц Корнелис  Эшер  

Альбрехт Дюрер гравюра «Меланхолия»                             картина  "Четыре тела"

продолжение

Мауриц Корнелис Эшер гравюра "Звезды»

 Сальвадор Дали «Тайная Вечеря»

Приложение 3

Кристаллы

            Кристалл двууглекислого натрия                                     Кристалл алмаза

                      Кристалл поваренной соли                                        Кристалл пирита

Кристалл бора

Вирусы и бактерии

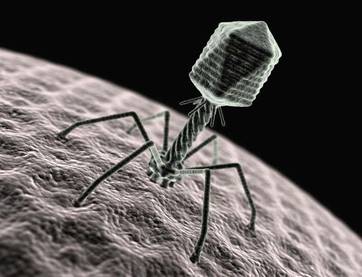
 Бактериофаги

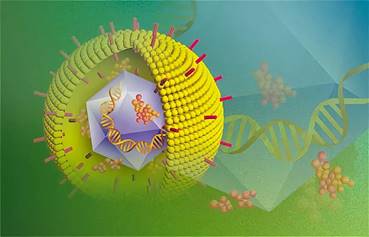
Вирус ветряной оспы

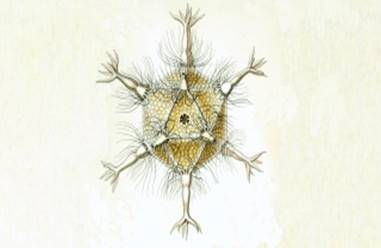
Морская Феодария

Скачано с www.znanio.ru