Исследовательский проект "Оценка выгодности условий вложения средств в различные проекты и кредитования"

Научное общество учащихся

Муниципальное автономное общеобразовательное учреждение

 «Школа с углублённым изучением отдельных предметов №85»

Сормовского района г.Н.Новгорода

«Оценка выгодности условий вложения средств в различные проекты и кредитования»

Выполнил:

                                                                 Научный руководитель:

Репьева М.В.,

                                                                 учитель математики

Нижний Новгород

2024год

Содержание

Введение. 3

Глава 1. Задачи о вкладах. 4

(банковских процентах) 4

1.1. Проценты по вкладам (депозитам) 4

Глава 2. Задачи о кредитовании. 10

2.1 Дифференцированные платежи. 10

2.2.Аннуитетные платежи. 16

Глава 3.  Задачи с различными условиями. 18

3.1.Наибольший доход от продажи ценных бумаг. 18

3.2. Оценка выгодности условий. 19

3.3 Проекты с дополнительным вложением средств. 23

3.3 Задачи оптимизации производства товаров и услуг 24  

Заключение. 26

Список литературы.. 27

Введение

Задачи с экономическим содержанием играют важную роль в математике.

Решение финансовых задач основывается на использовании различных математических моделей: уравнений, неравенств, их систем с привлечением процентов, арифметической и геометрической прогрессий и производной.

Я считаю, что это интересная тема для исследования. Она может пригодиться мне в будущем, при сдаче ЕГЭ и для участия в различных математических олимпиадах.

Актуальность проблемы вызвана тем, что многие люди не умеют правильно вкладывать свои средства в какие-либо проекты или берут кредиты под высокий процент, что приводит к лишним затратам.

Цель работы: проанализировать выгодность условий вложения средств в различные проекты, исследовать различные схемы кредитования.

Предмет исследования: различные экономические задачи (ситуации), связанные с товарно-денежными отношениями, минимизацией расходов и максимизацией прибыли

Задачи:

·     изучить теоретический материал по данной теме;

·     изучить эффективные методы решения задач с экономическим содержанием;

·     научиться применять изученный материал для решения конкретных задач.

Методы исследования: просмотр экономических лекций, изучение методических книг, где помогают научиться решать задачи на кредитование и вклады.

Гипотеза: используя умение решать задачи с экономическим содержанием, можно в реальной жизни минимизировать свои расходы и максимизировать прибыль.

Глава 1. Задачи о вкладах

(банковских процентах)

1.1. Проценты по вкладам (депозитам)

В задачах на проценты по вкладам речь идёт либо об однократном изменении величины вклада на определённое число процентов (простые проценты), либо о последовательном изменении величины вклада через (как правило) равные промежутки времени на определённое число процентов (сложные проценты). В «сложных процентах» каждый раз начиная со второго изменения, проценты начисляются на сумму, полученную после предыдущего начисления процентов. Тем самым задачи на проценты по вкладам представляют собой типичные задачи на последовательное изменение некоторой величины на определённое число процентов.

Чаще всего используют формулу: S_n =

Где S₀ – первоначальная сумма вклада,

 n- количество периодов,

x - количество процентов,

S_n - сумма на счету вкладчика.

Если S₀ — сумма вклада, то при начислении r_% на неё получим сумму

 S₁ = S₀ (1+ ) . При начислении г % на сумму S₁ получим

S₂ = S₁(1 +  )= S₀  и т. д. После n-го начисления процентов получим сумму :

S_n = S₀

Если при каждом начислении проценты меняются и составляют соответственно r_1%, r_2%, ..., r_„%, то

S_n = S₀ (1+)(1+)….(1+)

Отметим, что обычно в предложениях по вкладам (депозитам) речь идёт об определённом проценте годовых. Если этот процент начисляется раз в год, то проблем нет, соответствующие формулы приведены выше. Но в некоторых случаях речь может идти о вкладах с пролонгацией (продлением) через определённые промежутки времени (как правило, 1, 3 или 6 месяцев). В этом случае формулы расчёта процентов на депозиты меняются. При однократном начислении процентов через m дней на вклад S₀ под r_% годовых получим сумму:

S = S₀ (1+ ) (для обычного года)

или S = S₀ (1+ (для високосного года),

Сумма G начисленных процентов будет равна :

 для обычного года или   для високосного года.

На практике банки варьируют величину m в соответствии с реальным числом дней в каждом конкретном месяце (28, 29, 30 или 31 день).

Для приближённых расчётов может использоваться упрощённая модель, в соответствии с которой один месяц считается равным  части года. Тогда если речь идёт о вкладе на 3 месяца под r% годовых с последующей автоматической пролонгацией в течение нескольких раз, то каждые три месяца сумма на счёте вклада будет увеличиваться на % (так как три месяца составляют четверть года) и после n-й пролонгации сумма на счёте вклада составит S_n = S₀

Аналогично при пролонгации каждые полгода сумма на счёте вклада после п-й пролонгации составит S_n = S₀  Найденные значения обычно также округляются так, чтобы вычислить искомую сумму с точностью до копеек.

Задача 1.1.1. Какой вклад выгоднее: первый — на 1 год под 16% годовых или второй — на 4 месяца (с автоматической пролонгацией каждые четыре месяца в течение года с момента открытия вклада) под 15% годовых? При расчётах считайте, что один месяц равен  части года.

 Решение. Пусть S_o — сумма вклада. Тогда по условиям первого депозита вкладчик через год получит 1,16 S_o, а по условиям второго депозита он получит  S₀ = 1,157625 ∙ S_o, т. е. прибавка составит примерно 15,76%, а значит, первый вклад выгоднее.

Ответ: первый.

Задача 1.1.2. По вкладу «А» банк в конце каждого года увеличивает на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» увеличивает эту сумму на 25 % в течение каждого из первых двух лет. Найдите наибольшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет менее выгоден, чем вклад «А».

Решение. Пусть на каждый тип вклада была внесена сумма S. На вкладе «А» каждый год сумма увеличивается на 20%, т.е. умножается на 1,2. Тогда через 3 года сумма на вкладе «А» будет равна

Аналогично на вкладе «Б» сумма через три года будет равна:

где n– натуральное число.

По условию требуется найти наибольшее натуральное решение неравенства:

1,5625(1+)

1,5625+ S < 1,728S

1,5625∙S

0,015625 < 0,1655S

0,015625∙n < 0,1655

n < 10,592…

Так как n натуральное число, то n = 10.

Ответ:10.

Задача 1.1.3. Вклад планируется открыть на 4 года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наибольший размер первоначального вклада при котором через 4 года вклад будет меньше 25 млн рублей.

Решение.

Введем некоторые обозначения: S млн. рублей – размер первоначального вклада, r=10% - процент банка, x = 3 млн рублей, n=4 года -срок вклада.

По условию размер вклада через 4 года меньше 25 млн рублей;

S

S

S < 18,07

S<

S < 12, 34…..

Так как первоначальный вклад составляет целое число миллионов рублей, то

S = 12.

Ответ:12 млн рублей.

Задача 1.1.4. Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу?

Решение. S = 3600 тысяч рублей – сумма вклада

r_% - годовые проценты, r=10%

b=1+0,01 r,    b=1,1

n=3 года, х =? – добавочная сумма

S∙ +х∙ +x∙ b = 1,485∙ S

х∙ (+b) = 1,485∙ S - S∙

х∙ (1,21+1,1) = 1,485∙ S – 1,331∙  S

2,31х = 0,154 ∙ 3600

2,31х = 554,4

х = 240

Ответ: 240000.

Задача 1.1.5 .Близнецы Саша и Паша положили в банк по 50 000 рублей на три года под 10% годовых. Однако через год и Саша, и Паша сняли со своих счетов, соответственно 10% и 20% имеющихся денег. Еще через год каждый из них снял со своего счета, соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу третьего года на счету окажется большая сумма денег? На сколько рублей?

Решение: S=50000 – сумма вклада

r_% - годовые (ежемесячные) проценты, r=10%

b=1+0,01 r,   b=1,1

n=3 года, х – добавочная сумма

0,9S b3- 20000b = 0,9∙50000∙1,331–20000∙1,1 = 59895–22000 = 37895 (руб.)

0,8S-15000b = 0,8∙50000∙1,331–15000∙1,1 = 53240–16500 = 36740 (руб.)

37895 – 36740 = 1155 (руб.)

Ответ: у Саши окажется большая сумма денег на 1155 рублей.

Глава 2. Задачи о кредитовании.

2.1 Дифференцированные платежи.

Задачи на кредитование считаются более сложными по сравнению с задачами на вклады. При начислении процентов по кредиту обычно используются две схемы: схема с дифференцированными (неравными) платежами и схема с аннуитетными (равными) платежами. Эти схемы отличаются принципами формирования и величиной обязательных платежей.

В задачах по теме «Кредит» используют о три основных вида платежа:

1. Фиксированные платежи (платежи, которые чётко оговариваются в условии задачи)

2. Дифференцируемые платежи (ежемесячные или ежегодные платежи, уменьшающиеся к концу срока кредитования и обеспечивающие уменьшение суммы долга на одну и ту же величину)

3. Аннуитетные платежи (постоянные ежемесячные или ежегодные платежи, которые не меняются на протяжении всего периода кредитования)

Дифференцированные платежи

Пусть S_o — сумма кредита. Для кредита с дифференцированными платежами процент и периодичность обязательных платежей фиксируются (например, ежегодные, ежеквартальные или помесячные платежи), а фиксированный процент начисляется на ещё не выплаченную к моменту очередного обязательного платежа часть кредита (долга). В этом случае каждый год (или каждый платёжный период) сумма выплат уменьшается, поскольку она состоит из фиксированной части   (где n - число платежей, равное числу платежных периодов) и процентов, начисляемых на остаток долга по кредиту, величина которого каждый год (или каждый платёжный период) уменьшается на .  

Таким образом, при схеме с дифференцированными платежами клиент возвращает банку до истечения каждого платёжного периода - часть суммы кредита и проценты от еще не выплаченной на начало этого платёжного периода части кредита.

Рассмотрим сначала базовую (упрощённую) задачу на проценты по кредиту с дифференцированными платежами. Пусть кредит берётся под k % годовых на n лет. Это означает, что клиент должен вернуть банку сумму кредита (долг) и проценты за пользование кредитом на следующих условиях: каждый год клиент возвращает банку  часть суммы долга (кредита) и проценты за пользование кредитом, начисляемые ежегодно на остаток долга. Таким образом, за первый год пользования кредитом сумма G1  процентов составит:

G1= S0=

за второй год пользования кредитом сумма G2 процентов составит:

G2 = (S0 - )

за третий год пользования кредитом сумма G3  процентов составит:

G2 = (S0 - )   и т.д.;

за последний год пользования кредитом сумма Gn процентов составит:

Gn = (S0 - )

Общая сумма G всех начисленных процентов (переплата) находится

по формуле G = G1+... + Gn, откуда G = +

Вынесем за скобки общий множитель . Получим G = (n+(n-1)+…+1)

Выделенная сумма вычисляется по формуле:S=  суммы Sn первых n членов арифметической прогрессии {а_n}. В данном случае a1= 1,an = n.

Поэтому S_n= . Таким образом, G =

Общая сумма S всех выплат по кредиту равна сумме кредита и сумме начисленных процентов: S = S₀ + G, т. е. S = S_o +

Задача 2.1.1. 15 января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

• 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

• 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

Решение. Пусть сумма кредита равна S₀. По условию долг перед банком по состоянию на 15-е число должен уменьшаться до нуля равномерно, т. е. на  часть, поэтому суммы долга за каждый месяц (до начисления процентов) составят (в порядке убывания) : ,  , …, .

Первого числа каждого месяца долг возрастает на r %, поэтому последовательность размеров платежей по процентам будет следующей:

, …,

Ежемесячный платёж состоит из фиксированной суммы — и суммы платежа по процентам. Ежемесячные платежи составят соответственно:

Общая сумма выплат будет равна S = So +, откуда

S= + . По условию S = l,3. Следовательно,

1,3= So+ , откуда и r =3.

Ответ: 3

Задача 2.1.2 1 июля не високосного года Екатерина взяла в банке кредит на сумму 109500 рублей под 24% годовых сроком на 6 месяцев на условиях погашения кредита дифференцированными платежами. Это означает, что до 1 числа каждого следующего за июлем месяца она вносит в банк платеж, состоящий из  части долга (т. е. 18 250 рублей) и процентов, которые начисляются с учётом числа дней соответствующего месяца: 30 или 31 (всего 6 платежей). Найдите сумму всех выплат по кредиту.

Решение. 

Cумма всех выплат в рублях по процентам (переплата) составит

S = S1 + ... + S6 = 2232 + 1860 + 1440 + 1116 + 720 + 372 = 7740, а общая сумма выплат: G = 109 500 + 7740 = 117 240.

Ответ: 117 240.

Задача 2.1.3. В июле планируется взять кредит в банке на сумму 10 млн рублей на 5 лет. Условия его возврата таковы:

·        каждый январь долг возрастает на 10% по сравнению с концом предыдущего года

·         с февраля по июнь каждого года необходимо выплатить часть долга

·         в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года

Сколько миллионов рублей составила общая сумма выплат после погашения кредита?

Решение.  Обозначим то, что нам дано: S=10 млн руб. – сумма кредита, n=5 лет, a= 10% -процент банка, m= 1+  x-ежегодные выплаты.

 X1+ x2 +x3+x4+x5 =3+2,8+ 2,6+ 2,4+ 2,2 = 13 млн рублей

Ответ: 13 млн рублей.

2.2.Аннуитетные платежи

Начнём с упрощённой реальной схемы, предполагающей ежегодные, а не ежемесячные выплаты. По-прежнему будем считать, что So — сумма кредита (долга) и кредит берётся на n лет под k % годовых. Эта же схема применима и в тех случаях, когда процент по кредиту указывается для платёжного периода, а не для полного года.

Для реальных кредитов с аннуитетными платежами условия начисления процентов оказываются следующими:

• до истечения очередного платёжного периода банк начисляет k % на оставшуюся сумму долга, г. е. увеличивает её на k %;

• после начисления процентов клиент вносит в банк (также до истечения соответствующего платёжного периода) некоторую сумму x — одну и ту же для каждого платежа; сумма долга при этом уменьшается, и на эту уменьшенную на x сумму начисляются проценты до истечения следующего платёжного периода, после чего клиент вносит в банк платёж в размере той же суммы x и т. п.

Из этих условий и находится сумма х регулярного платежа. Для её вычисления запишем суммы долга по истечении каждого платёжного периода, обозначив         буквой m: Sx = m— х,

S2 = m∙S1- x = ∙ - mx- x,

S3 = m∙S2 - x = ∙ - x-mx - x,

Sn = m∙ - x=  — x- ...- m∙x — x.

Поскольку по истечении последнего платёжного периода долг равен 0, получаем, что  = 0, т. е. - х-…- mх- х = 0. Отсюда х + mх + ... +  х = , или (после вынесения общего множителя в левой части последнего равенства)       х(1 + m+ ... + m) = .

Сумма 1+ m+…+ вычисляется по формуле S =   суммы S первых n членов геометрической прогрессии {}. В данном случае  = 1, q = m. Поэтому     Sn =. Таким образом, х = o, откуда x=.

Число А= называется коэффициентом аннуитета. Часто его вычисляют, записывая годовой процент в сотых долях (т. е. в виде десятичной дроби), для чего обозначают (или 0,01k) буквой P.

Тогда m = p + 1 и А =  . Формула (3) при этом примет вид x= (4)

Последняя формула позволяет находить сумму регулярного платежа и для любого периодического платежа. При этом считают, что p —это процентная ставка, выраженная в сотых долях в расчёте за этот период. Например, для n ежемесячных платежей по кредиту под 12%  годовых p = = 0,01, и если кредит берётся сроком на 10 лет, то x= 0. Ясно, что вычисления по подобным формулам без применения специальных (хотя и несложных) программ будут, мягко говоря, затруднительными. Так, если считать, что сумма кредита на 10 лет под 12% годовых равна 1 000 000 руб., то

х = 0,01434711000000 = 14347,1(руб.)

Общая сумма S выплат находится по формуле

S = 120∙х = 120 ∙ 14 347,1 = 1 721 652 (руб.)

Сумма G выплаченных процентов (переплата) составит 721 652 руб., т. е. примерно 72,17% от суммы кредита.

Глава 3.  Задачи с различными условиями

3.1.Наибольший доход от продажи ценных бумаг.

Задача 3.1.1 .

Семён приобрёл ценную бумагу за 8 тыс. рублей. Цена бумаги каждый год возрастает на 1 тыс. рублей. В любой момент Семён может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 8%. В течение какого года после покупки Семён должен продать ценную бумагу, чтобы через 25 лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Решение. Если бы Семён продал бумагу в начале покупки и положил вырученные деньги на банковский счёт, то через 25 лет на его счету была бы сумма:

 S_n =

S₂₅ = 8= 8

А если бы он сделал тоже самое вначале следующего года с момента приобретения, то через 24 года на его счету была бы сумма:

(8+1)  = 9

Мы определили, что Семёну будет выгоднее продать бумагу в течение 6 года с момента покупки.

Ответ: в течение 6 года с момента приобретения.

3.2. Оценка выгодности условий

Задача 3.2.1. По вкладу А банк в течение трех лет в конце каждого года планирует увеличивать на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу Б - увеличивать эту сумму на 5% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад 5 окажется выгоднее вклада А при одинаковых суммах первоначальных взносов.

Решение:

Пусть S - сумма вклада, r - процентная ставка

1)  Вклад А :    

S – сумма на вкладе А через 3 года.

2) Вклад Б :  ;

1,05S -сумма на вкладе Б через 3 года,

 Чтобы вклад Б оказался выгоднее, чем А, должно выполняться следующее неравенство:

1,05S>S|:S

1,05>

1,05>1,331.                      (1)

Требуется найти наименьшее целое число n, для которого неравенство (1) верно.

При n = 12 неравенство (1) неверно, т.к. 1,05  =1,317…>1,331

При  n =13 неравенство (1) верно, т.к  1,05 =1,341… >1,331

Следовательно, наименьшее целое значение значение n, при котором за три года хранения вклад Б окажется выгоднее вклада А, равно 13.

Ответ 13.

Задача 3.2.2.

В июле планируется взять кредит на сумму 4026000 р. Условия его возврата таковы:

- в январе каждого года долг возрастает на 20 % по сравнению с концом прошлого года;

- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.

На сколько рублей больше придется отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (т.е. за 4 года), по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (т.е. за 2 года)?

S=4026000 р.

r=20%    k=1+=1+

1)    n=2 года

(Sk-x)k-x=0

S-xk-x=0

S=xk+x

S=x(k+1)

x(k+1)= S

x=

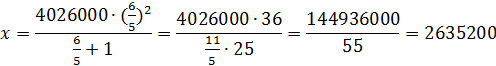
2)    n=4 года

(((Sk-y)(k-y)(k-y)k=0

S

y=

y==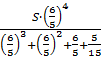

4y-2x=41555200-22635200=6220800-5270400=950400 (р.)

Ответ: на 950400 рублей

Задача 3.2.3.

Пенсионный фонд владеет ценными бумагами, которые стоят  тыс. р. В конце года t (t=1, 2, …) В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счет в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться 1 + r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце 25-го года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце 21-го года. При каких положительных значениях r это возможно?

Решение:

В конце года стоимость ценных бумаг растет по заданному закону продолжительное время. Будем считать, что одно и то же кол-во бумаг стоит в конце 1-го, 2-го, … , 25-го годов соответственно

Проведём расчеты на тот случай, если продать ценные бумаги в конце любого из этих годов, кроме последнего и деньги положить на счёт в банке. Сумма оставшаяся до 25-ти лет будет увеличиваться в 1+r раз.

По условию задачи сумма в конце 25-го года будет наибольшей , если продажа состоялась в 21-ом году, т.е. наибольшая сумма равна

Из сравнения этой суммы с соседними членами последовательности (1) получим два неравенства:

Первое неравенство разделим на положительное число , второе – на . Получим границы для величин 1+r и r:

Неравенство (2) даёт границы для r , полученные из условия, что для членов последовательности (1) справедливы неравенства

 Покажем теперь, что для членов последовательности (1) справедливы неравенства.

Так как =

,то поэтому  .

Ответ:

3.3 Проекты с дополнительным вложением средств.

Задача 3.3.1

По бизнес-плану предполагается вложить в четырёхлетний проект
10 млн р. По итогам каждого года планируют прирост вложенных средств на 15% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число и млн р. в первый и второй годы, а также целое число т млн р. в третий и четвёртый годы. Найдите наименьшие значения п и т, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся.

Решение:

Первоначальными вложениями являются 10 млн р. Рассмотрим изменения средств (в миллионах рублей), вложенных в проект, за первые два года. В конце первого года сумма 10 увеличилась в 1,15 раза и к ней прибавили n. В конце второго года те же действия выполнили с суммой     11,5 + n.

Так как первоначальные вложения за два года как минимум удвоятся, то верно неравенство

 Так как n - число целое и при n = 3 данное неравенство неверно, а при n = 4 - верно,  то наименьшее целое число n, для которого неравенство верно, равно 4.

Продолжим заполнение таблицы согласно условиям задачи для 3-го и 4-го годов, учитывая, что n = 4.

Так как первоначальные вложения за четыре года как минимум утроятся, то верно неравенство

Так как m - целое число и при m=0 это неравенство неверно, а при m=1 верно, то наименьшее целое число m, для которого данное неравенство верно, равно 1.

Ответ: n=4 млн. рублей, m= 1млн рублей.

3.4 Задачи оптимизации производства товаров и услуг.

Задача 3.4.1.

Строительство нового завода стоит 78 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5х² + 2х+ 6 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит                    рх - (0,5х² + 2х +6). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более чем за 3 года?

Решение:

Прибыль фирмы за 1 год ( в млн. рублей) составит:

px-(0,5х² + 2х +6) =px-0,5х² - 2х –6 =-0,5х² + (p-2) x-6.

Рассмотрим функцию

y(x)= -0,5х² + (p-2) x-6 - квадратичная функция,

график – парабола , ветви которой направлены вниз и свое максимальное значение достигает при x=x₀,  х₀=

x_{0 =}

Тогда наибольшая прибыль за год равна:

-0,5(p-2)² +(p-2)²-b= 0,5(p-2)²-6

А за 3 года наибольшая прибыль составит

3(0,5(p-2)²-6)= 1,5(p-2)²-18

Найдем наименьшее значение p,при котором верно следующее неравенство

тогда

Наименьшее решение неравенства будет

Ответ: при p=10.

Заключение

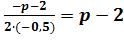
В результате своей работы я научился решать экономические задачи нескольких видов, аналогичных заданиям № 16 ЕГЭ профильного уровня.

Полученные знания и приобретенные умения решать задачи с экономическим содержанием, можно использовать в реальной жизни, для того, чтобы минимизировать свои расходы и максимизировать прибыль.

 Поставленная мной в начале цель была достигнута.

Список литературы

1.                 С.А. Шестаков под редакцией И.В. Ященко ЕГЭ 2021.Математика // Задачи с экономическим содержанием. (Задача №17 профильный уровень). Москва 2020.

2.                 А.Ф. Карелин Методическое руководство по решению задач о кредитном контракте, основанном на дифференцированной системе платежей. (задача №17 из вариантов ЕГЭ профильного уровня по математике). Москва 2018.

3. Методические указания к решению задач ЕГЭ для школьников. (Белгородский государственный технологический университет им. В. Г. Шухова)

4.Интернет – ресурсы

4.1https://ege.sdamgia.ru/test?theme=292&ysclid=lrjdigndun184472005

4.2https://3.shkolkovo.online/

4.3https://ped-kopilka.ru/blogs/blog58271/reshenie-yekonomicheskih-zadach-na-kredity.html?ysclid=lrjdj9ftqq107491191

4.4https://100ballnik.com/wp-content/uploads/2021/09/kredity_ege.pdf?ysclid=lrjdjhjuqj990285007

4.5https://4ege.ru/

Скачано с www.znanio.ru