Коллапс волновой функции как структурный переход во времени S

© О.С. Басаргин

Аннотация

Предложена модель коллапса волновой функции как непрерывного фазового перехода через переходную зону в параметрическом времени S. В отличие от стохастических моделей GRW и CSL, в данной схеме переход инициируется внутренней антисимметричной структурой времени (S-фрагментом Сфирали), без нарушения унитарности и без внешнего шума. Коллапс описывается модифицированным уравнением Шрёдингера с дополнительным фазозависимым оператором 𝑉̂_S(s), локализующим разрушение суперпозиции в области перехода. Выведены формы γ(s), моделирующие временную локализацию эффекта. Предложены экспериментальные сценарии проверки (слабые измерения, фазовое вмешательство), а также возможности применения в квантовой информации, космологии и когнитивных науках.

1. Постановка задачи

В стандартной квантовой механике коллапс волновой функции — аксиоматический процесс, не описываемый уравнениями Шрёдингера. Он считается мгновенным и нереверсируемым, возникающим при акте измерения. Возникает вопрос: можно ли описать коллапс как физический переход, происходящий по определённой внутренней структуре, а не как формальный скачок?

2. Гипотеза сфирального коллапса

Коллапс волновой функции трактуется как фазовый переход через переходную S-зону во времени S, возникающий при взаимодействии с измерительной системой. Состояние эволюционирует по антисимметричной структуре:

•       на витке — унитарная эволюция ψ(s) = A(s)^eiφ(s);

•       в S-зоне — нелинейная перестройка фазы φ(s), приводящая к актуализации одного из возможных исходов;

•       после петли — фиксация результата и подавление когерентных компонент.

Коллапс — не точечное событие, а локализованная зона фазового преобразования, в которой система теряет суперпозиционную структуру и приобретает определённое значение наблюдаемой. 3. Уравнение структурной эволюции

Обобщённое уравнение Шрёдингера во времени S:

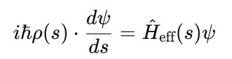
Внутри S-зоны:

где 𝑉̂_S(s) — нелинейный, фазозависимый оператор деформации:

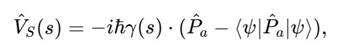
где 𝑃̂_а — проектор на одно из собственных состояний оператора наблюдаемой величины 𝐴̂.

4. Форма γ(s)

Функция γ(s), отвечающая за локализацию эффекта перехода, может быть выбрана, например, как:

•       Гауссов импульс:

•       Cигмоид:

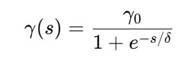
Эти формы обеспечивают плавное, но локализованное действие оператора 𝑉̂_S(s) вблизи S-зоны.

5. Последствия и интерпретации

•       Коллапс становится непрерывным фазовым процессом с характерным временным масштабом τ ∼ σ/ρ₀;

•       Вероятность исхода определяется значением ∣A(s)∣² до входа в S-зону;

•       Повторное измерение вблизи начала фазы может восстановить когерентность — в случае неполной деформации;

•       Открывается возможность обратного хода при симметричном прохождении S-зоны в противоположном направлении, в рамках антисимметрии сфиральной структуры времени.

6. Сравнение с моделями GRW, CSL и возможности экспериментальной верификации

6.1. Сравнение с GRW и CSL

Модели GRW (Ghirardi–Rimini–Weber) и CSL (Continuous Spontaneous Localization) вводят спонтанные, стохастические модификации уравнения Шрёдингера, вызывающие коллапс без наблюдателя. Они предполагают:

•       наличие дополнительного нелокального шума;

•       разрыв унитарности;

•       стохастический характер коллапса.

Отличие сфирального подхода:

•     Коллапс реализуется не стохастически, а через топологический механизм фазового перехода;

•       Уравнение остаётся детерминированным и локальным во времени s;

•       Вместо шума действует геометрическая структура (антисимметрия и S-зона), локализующая переход;

•       Сверхпозиция разрушается постепенно и обратимо при определённых условиях, что невозможно в GRW и CSL.

Таким образом, сфиральный коллапс ближе к динамически-геометрической интерпретации, чем к стохастическим схемам.

6.2. Экспериментальная проверка

Наиболее подходящий класс экспериментов — непрерывные слабые измерения квантовых систем в реальном времени. Примеры:

•       Minev et al. (2019): регистрация квантовых прыжков в сверхпроводниковом кубите. Переход к измеренному состоянию происходил плавно, с возможностью прервать процесс;

•       Pokorny et al. (2020): слежение за квантовой системой в процессе перехода, отображающее нелинейную динамику с характерной кривизной траектории состояния.

Предсказания сфиральной модели:

•       Наличие характерного временного масштаба фазовой перестройки τ;

•       Возможность отката при вмешательстве в зону S до завершения перехода;

•       Асимметрия фазового сдвига между путями, проходящими через разные ветви сфирали;

•       Фазовая зависимость вероятности результата — не только через величину, но и через ориентацию φ(s).

6.3. Дальнейшие шаги

•       Формализация явного вариационного принципа для сфирального коллапса;

•       Сравнительные численные расчёты с моделями GRW и CSL;

•       Поиск макроскопических следствий (например, корреляции между измерениями при искусственной модуляции γ(s)).

7. Сводка гипотезы и перспективы интеграции сфиральной модели коллапса

7.1. Обобщение модели

Сфиральная модель интерпретирует коллапс волновой функции как фазовый переход через локализованную S-зону в параметрическом времени ss. Процесс формализуется как непрерывная эволюция по модифицированному уравнению Шрёдингера, где дополнительный оператор 𝑉̂_S(s) реализует направленную деформацию фазы с геометрическим (топологическим) источником.

Ключевые отличия модели:

•       Коллапс — геометрически организованный переход, а не стохастический разрыв;

•       Форма и скорость коллапса определяются вложенной фазовой функцией γ(s), а не случайным флуктуационным процессом;

•       Обратимость возможна, если система остаётся внутри переходной зоны;

•       Эволюция происходит в собственном времени системы (s), а не во внешнем параметре t.

7.2. Потенциал интеграции

•       В квантовую механику: возможна переформулировка измерительного постулата через геометрическую эволюцию;

•       В интерпретации: сфиральная модель может быть объединена с деБройль–Бомовской (через фазовое поле) или модифицировать многомировую (через фракционирование витков);

•       В квантовую информацию: применение в моделях фазового контроля над когерентностью, управляемых коллапсом;

•       В космологию: коллапс как механизм выбора классического мира при квантовом разветвлении ранней Вселенной;

•       В когнитивные модели: фазовое "решение" как прохождение через внутреннюю S-зону субъективного выбора.

7.3. Следующие шаги

•       Разработка численной реализации модели для простейших квантовых систем;

•       Анализ связности с трёхмерными алгебрами и тринглом (в рамках проекта H₃);

•       Экспериментальные предложения по фазовому контролю в сверхпроводниковых и фотонных системах;

•       Связывание с другими сфиральными моделями (времени, сознания, топологической динамики).

Сфиральная модель открывает путь к объединённому описанию измерения, времени и актуализации как единого топологического процесса, устраняя границу между динамикой и выбором.

Выводы

1.     Коллапс волновой функции может быть интерпретирован не как аксиома, а как физический процесс — фазовое прохождение через структурную зону времени, описываемую моделью Сфирали.

2.     Введён параметр s, в котором эволюция квантового состояния сохраняет унитарность вне зоны коллапса, но приобретает управляемую деформацию в пределах перехода.

3.     Коллапс становится обратимым при неполной фазовой перестройке, что отличает модель от GRW и CSL и открывает возможность нового типа квантового управления.

4.     Модель не требует внешнего шума и сохраняет локальность во внутреннем времени s, а не во внешнем t.

5.     Возможна экспериментальная проверка в системах с фазовой чувствительностью (кубиты, нейтроны, фотонные сети), в том числе через прерывание или усиление перехода в S-зоне.

6.     Сфиральная модель может быть встроена в существующие интерпретации квантовой механики, а также расширена до описания выбора, сознания и космогенеза как топологического акта.

Модель открывает путь к новой фазовой онтологии в квантовой теории, где процессы выбора и актуализации встроены в геометрию самого времени.