Создание электронного пособия к разделу Молекулярная физика

Приложение 6

Управление образования г. Ленинска - Кузнецкого

МОУ «Гимназия №12»

НОУ «Интеллектуал»

Секция «Физика и познание мира»

Апарин Александр Олегович

Скопенцов Дмитрий Викторович

Терентьев Анатолий Вячеславовчи

Создание электронного пособия к разделу

”Молекулярная физика ”

Научный руководитель

                                                                            Пронуза Н.В.

                                                                                 учитель физики

МОУ «Гимназия №12»

____________________

                                                                                                              (подпись)

Ленинск-Кузнецкий

2007

Содержание

Введение………………………………………………………………………...3

Глава 1. Обобщение научной и научно-учебной литературы

по Молекулярно-кинетической теории.……………….………..……………5

Глава 2. Анализ возможностей программы Flash 6………………….…......16

Глава 3. Моделирование физического эксперимента на компьютере….....20

Заключение……………………………………………………………………29

Список литературы………………………………………………………...…32

Приложение. Электронное пособие…………………………………...…….34

Введение

          Современный период развития российского общества называют этапом информатизации. Информатизация общества предполагает всестороннее и массовое внедрение методов и средств обработки, передачи, хранения информации на базе средств электронно-вычислительной техники. Одним из важнейших направлений процесса информатизации общества является информатизация образования.

         Информатизация- это одно из направлений приоритетного национального “Проекта образования “, это одно из актуальных направлений развития нашей гимназии.

         Сейчас разрабатывается Программа экспериментальной деятельности по информатизации образования на областном уровне. Программа предполагает активное использование новых информационных технологий в учебном процессе на уроках, на индивидуальных занятиях, в научно-исследовательской деятельности учащихся.

         Все вышесказанное обуславливает актуальность выбранной темы ”Создание электронного пособия к разделу «Молекулярная физика ».

         Объект исследования – моделирование газовых процессов в разделе “Молекулярная физика”

         Предмет – создание электронного пособия к разделу «Молекулярная физика», используя возможности программы Flash.

         Цель исследования – создание электронного пособия к разделу  “Молекулярная физика”, используемого на уроках для изучения процессов в газах.

         Цель предполагается достичь путем решения следующих задач:

1.     Обобщить научную и научно-учебную литературу по Молекулярно–  кинетической теории;

2.     Проанализировать возможности программы Flash:

3.     Смоделировать некоторые газовые процессы на компьютере.

К создаваемому пособию предъявляются определенные требования:

1. Компактность изложения материала;

2. Наличие теоретического материала по теме и экспериментальной части;

3. Возможность выполнения лабораторных работ с изменением вводимых параметров;

4. Удобство использования на уроке и на индивидуальных занятиях;

5. Визуальная доступность, привлекательность изложенного материала и другие.

Глава 1. Обобщение научной и научно-учебной литературы по Молекулярно-кинетической теории.

В энциклопедическом словаре молекулярная физика представлена, как наука, изучающая физические свойства и агрегатные состояния  тел в зависимости от молекулярного строения, взаимодействия между молекулами и характера их теплового движения. Имея дело с огромными совокупностями молекул, молекулярная физика широко использует статистические законы и законы термодинамики. Молекулярная физика тесно связана с другими физическими науками, особенно с атомной физикой и физической химией, а также с техническим материаловедением.

В основе молекулярно-кинетической теории или просто молекулярной физики лежат три важнейших положения:

1)    Все тела состоят из огромного количества частиц (молекул, атомов или ионов), между которыми есть промежутки

2)    Частицы вещества непрерывно и хаотично движутся

3)    Частицы вещества взаимодействуют друг с другом, притягиваются на небольших расстояниях и отталкиваются, когда эти расстояния уменьшаются.

На сегодняшний день накоплен огромнейший материал в термодинамике, статической физике и статической термодинамике. Термодинамика – теория, в которой изучаются тепловые свойства макроскопических тел без учета их молекулярного строения. Статистическая физика учитывает микроскопическое строение вещества и использует микроскопические параметры состояния отдельных молекул. Статистическая термодинамика – раздел статистической физики, посвященный обоснованию термодинамических законов и выяснению макроскопических параметров состояния тел  [9;98]

         В 1827 г. английский ботаник Р. Броун наблюдал в микроскоп взвесь цветочной пыльцы в воде. То, что он увидел, очень его удивило. Писал он об этом так: «При работе с частицами или зернами необычайно малой величины, размером от одной четырехтысячной до одной пятитысячной доли дюйма (т.е. 5-6 мм) в длину, погруженными в воду, я наблюдал многие из них в явном движении.… Эти движения были таковы, что после многих повторных наблюдений я убедился в том, что они возникают не от потоков жидкости и не от ее постоянного испарения, а принадлежат самим частицам». Броун также отметил, что частицы двигались непрерывно, описывая самые причудливые траектории; их движение носило ярко выраженный хаотический характер. Качественно объяснить причины броуновского движения удалось только через 50 лет - лишь в конце 70-х гг. XIX века причину «броуновского движения» стали связывать с ударами молекул жидкости о поверхность взвешенных в ней частиц. Если бы частица была большой, то молекулы равномерно толкали бы ее со всех сторон и взвешенная частица оставалась  бы на месте. Но маленькая частица имеет маленькую поверхность, и толчки не уравновешивают друг друга. Равнодействующая их  сил не равна нулю, а все время меняется по величине и направлению. В результате частица блуждает случайным образом по жидкости.

Первая количественная теория броуновского движения появилась в 1905 г. Ее автором был Альберт Эйнштейн, опубликовавший классическую работу «О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты».

В своей работе Эйнштейн показал, что случайные блуждания броуновских частиц можно трактовать следующим образом: они участвуют в  тепловом движении наравне с молекулами той среды, в которой они взвешены, обладая в среднем такой же  кинетической энергией, но несравненно меньшей скоростью ввиду гораздо большей массы. Измерив смещение частицы за определенное время, зная ее радиус и вязкость жидкости, можно вычислить число Авогадро. Экспериментально подтвердил теория Эйнштейна   французский физик Ж. Перрен. Проследив за движением нескольких тысяч частиц эмульсии в плоской кювете глубиной 0,1 мм и подставив свои данные в формулу Эйнштейна, Перрен в результате довольно точно вычислил значение числа Авогадро.

К моменту создания уравнения идеального газа была уже сформулирована кинетическая теория. Она исследует процессы, происходящие в веществе, исходя из тех молекулярных движений, которые совершают частицы вещества. Основная  идея теории заключается в том, что материальные тела состоят из мельчайших частиц (атомов, молекул), находящихся в непрерывном движении. Быстрое развитие кинетической теории началось лишь в середине XIX века в связи с развитием теории газов, тепловых машин и термодинамики. Наиболее ранней и наиболее развитой является кинетическая теория газов. Основной вклад в нее внесли Р. Клаузиус (1822-1888), Дж. Максвелл (1831-1879) и Л. Больцман (1844-1906). В развитии кинетической теории газов большую роль сыграло представление молекулы в виде абсолютно твердых, упругих шариков.

Согласно кинетической теории, частицы (атомы, молекулы) в газе находятся на расстояниях друг от друга, больших по сравнению с их размерами, движутся прямолинейно и равномерно, изредка сталкиваясь друг с другом и со стенками сосуда. Удары молекул о стенки сосуда создают  давление газа. Оно пропорционально числу молекул в единице объема и среднему значению их кинетической энергии.

Столкновения между частицами газа очень важны для релаксационных процессов. Так называются процессы, приближающие газ к тепловому равновесию в условиях однородного давления. Сюда относятся процессы диффузии (перемешивания разных газов), теплопроводности (выравнивания температуры)  и вязкости (или внутреннего трения), проявляющиеся в прекращении движения газа как целого в неподвижном сосуде. Кинетическая теория позволяет рассчитать скорости этих процессов.

         В 1857 году немецкий физик Рудольф Клаузиус вывел модель идеального газа (первоначально «совершенный газ»). Идеальный газ – теоретическая модель, в которой пренебрегается взаимодействием молекул (за исключением сил отталкивания, возникающих при их непосредственном столкновении друг с другом), а сами молекулы (в промежутках между столкновениями) рассматриваются как не имеющие размеров материальные точки.

 В 1834 Клапейрон ввел в термодинамику графический метод, представив в геометрической форме рассуждения Карно. В том же году вывел уравнение состояния идеального газа (уравнение Клапейрона), объединяющее закон Бойля – Мариотта, закон Гей-Люссака и закон Авогадро. Это было наиболее простое соотношение, применимое с определенной степенью точности к реальным газам при низких давлениях и высоких температурах. Выведено оно при допущении, что молекулы газа представляют собой материальные точки: обладая массой, но не имеют объема и никак не воздействуют между собой. Поэтому оно и названо уравнение состояния идеального газа. Такое допущение определяет область, в которой применяется это уравнение:  при низком давлении газ занимает настолько большой объем, что объемом самих молекул можно смело пренебречь, а при высокой температуре молекулы обладают такой большой энергией и такой большой скоростью, что взаимное притяжение не влияет на их движение.

В 1834 году им была опубликована работа, в которой он широко использовал объединенный газовый закон, нигде не говоря, однако, что его автором является Карно. Этот закон Клапейрон впервые представил в виде: 

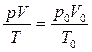
где через p₀, V₀, T₀  обозначены параметры начального состояния газа, а через p, V, T (температура в кельвинах) – параметры его конечного состояния

К середине XIX века были установлены основные опытные закономерности, которым подчиняются газы. При переходе данной массы газа из одного состояния, характеризуемого параметрами p₀, V₀ , T₀, в другое, характеризуемое параметрами p, V, T, могут меняться все перечисленные величины, а могут только две из них, а третий оставаться неизменным. Процессы, при которых один из параметров состояния газа остается неизменным, называют изопроцессами. Если неизменным параметром является температура, то соответствующий изопроцесс называют изотермическим (от греч. «терме» - теплота), если объем, то изохорным (от греч. «хора» - занимаемый объем), а если давление, то изобарным ( от греч. «барос» - тяжесть).

1) Изотермический процесс (при T=const и m=const)

     pV=const

         Первый газовый закон: при неизменной температуре произведение давления данной массы идеального газа на его объем является величиной  постоянной

         В Англии этот закон называют законом Бойля, во Франции – Мариотта, а у нас – законом Бойля-Мариотта. Он был открыт экспериментальным путем задолго до создания статистической термодинамики. В 1661 году английский любитель физики Р. Тоунли впервые высказал гипотезу о постоянстве произведения pV. В том же году лорд Броункер и врач Пауэр провели опыт по проверке  этой гипотезы. В  это же время в наиболее широких пределах эта гипотеза была подтверждена экспериментами английских ученных. Роберт Бойль  опубликовал свои результаты в 1662, причем по полноте и точности они намного превосходили данные других исследователей, среди этих исследователей был и Роберт Гук, который уже в 1660 году располагал данными, согласующимися с гипотезой Тоунли. Для графического представления изопроцессов Клапейрон предложил использовать системы координат, по осям которых откладываются параметры состояния газа. Графики изотермического процесса получили название изотерм.

Изотермический процесс (T=const): pV=const – закон Бойля-Мариотта: p₁V₁=p₂V₂: p=const/V

                   В трактате “Гидродинамика”, вышедшем в свет в 1738г. он первым в истории физики пытается объяснить нагревание тел увеличением скорости движения частиц, согласно Бернулли, они двигаются с большими скоростями в разных направлениях. « Упругость воздуха повышается не только вследствие сгущения, - пишет он в своем трактате, - но и вследствие увеличения теплоты, ибо известно, что везде, где возрастает внутреннее движение частиц, теплота повышается». Это четкое утверждение автора долгое время не встречало поддержки.

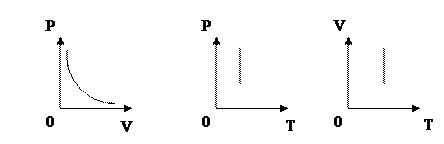
2) Изохорный процесс (V=const)

                    (при V=const и m=const)  или  p=const T

         Второй газовый  закон: при неизменном объеме отношение давления данной массы идеального газа к его абсолютной температуре является величиной постоянной. 

         Впервые гипотеза о пропорциональности давления и температуры была высказана в 1702 году французским физиком Гильомом Амонтоном. Однако, точная формула соответствующего закона была получена лишь через сто лет французским ученым Ж.Л. Гей-Люссаком [2, 146]. Графики изохорного процесса называются изохорами.

Изохорный  процесс (V=const): - закон Гей-Люссака

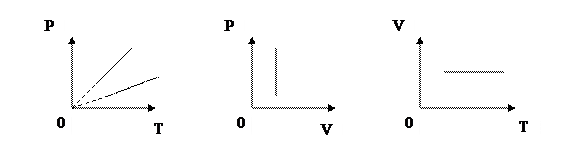
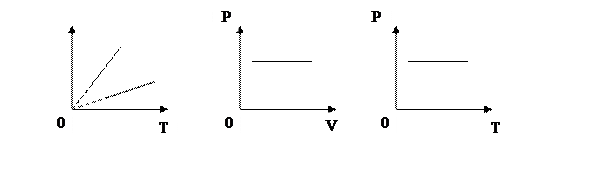
3) Изобарный процесс (p=const)

         Третий газовый закон: при неизменном давлении отношение объема данной массы идеального газа к его абсолютной температуре является величиной постоянной.

                     (при p=const и m=const) или  V=const T

         Третий газовый закон был открыт в 1787 году французским физиком Жаком Шарлем. Однако, Шарль не опубликовал результаты своих экспериментов. Лишь через 15 лет к тому же выводу пришли английский ученый Джон Дальтон, и французский физик Жозеф Луи Гей-Люссак. Гей-Люссак сформулировал свой вывод более определенно, в отличии от Дальтона. Однако, сам Гей–Люссак  с благородством, которое редко можно встретить в вопросах приоритета, настоял на том, чтобы этот закон назвали в честь Шарля. Графики изобарного процесса называют изобарами.

Изобарный процесс (p=const):- закон Шарля

(закон Гей-Люссака в отечественной литературе)  

Состояние газообразных тел определяется их объемом, давлением и температурой, поэтому физические величины p,V,T называют макроскопическими параметрами состояния. Уравнение, выражающее связь между макроскопическими параметрами состояния вещества, называют уравнением состояния этого вещества.

         Установление вида этой связи, т.е.   уравнение состояния того или иного тела, является основной задачей молекулярно-кинетической теории вещества. Точное решение этой задачи для единичной системы для идеального газа получено нашим отечественным выдающимся ученым Дмитрием Ивановичем Менделеевым.

         Ранее мы уже дали понятие идеального газа, введенное Клаузиусом. В общем случае газ называют идеальным, если:

1)        Размеры молекул малы по сравнению с расстояниями между ними;

2)        Молекулы взаимодействуют друг с другом и со стенками сосуда только в момент соударения;

3)        Все соударения абсолютно упругие;

4)        Рассматриваются любые газы, в которых число молекул очень велико;

5)        Молекулы распределены по всему объему равномерно;

6)        Молекулы движутся хаотично, то есть все направления движения молекул равноправны;

7)        Скорости молекул могут принимать любые значения;

8)        К движению отдельной молекулы применимы законы классической механики.

Положение 1 и 2 следуют из сведений о размерах и взаимодействиях молекул. Положение 3 опирается на свойства броуновского движения,  самой удивительной чертой которого является его постоянство, свидетельствующее об абсолютно упругом соударении молекул. Положение 4 можно пояснить примером: в  1мм³ комнатного воздуха содержится 2,7*10¹⁰ молекул. Положения 5 и 6 имеют свое опытное обоснование в одинаковом давлении  газа в разных местах сосуда, в котором он находится, законе Паскаля и традиционном движении. А вот справедливость постулатов 7 и 8, а также границы их применимости, может подтвердить только контрольный эксперимент, с точки зрения современной  физики, скорости тел не могут быть сколь угодно  большими (предельной скоростью является скорость света в вакууме c=3*10⁸ м/с). Однако, можно предположить, что молекул с очень большими и очень маленькими скоростями, в газе относительно немного.

Реальные газы (например, кислород и гелий) в условиях, близких к нормальным,  а также при низких давлениях и высоких температурах -  близки к идеальным газам. Частицы идеального газа в промежутках между столкновениями движутся равномерно и прямолинейно. Давление газа на стенки сосуда можно рассматривать как ряд быстро следующих ударов газовых молекул о стенки.

Развитие термодинамики и статистической физики в конце XIX века создало благоприятную почву для создания уравнения Менделеева–Клапейрона. Менделеев брал за основу уравнение Клапейрона. Он обобщил его в 1874году. Итак, уравнение вида:

,  где – универсальная газовая постоянная, называют уравнением Клапейрона - Менделеева.

Из уравнения Клапейрона - Менделеева можно вывести ряд простых, но важных следствий:

1) Многие газовые реакции происходят при постоянной температуре и давлении. При этих условиях , уравнение  есть не что иное, как закон Авогадро, который утверждает, что в равных объемах газов при постоянных температуре и давлении содержится одинаковое число молекул.

2) Другое интересное следствие касается плотности газов. Из  уравнения   следует, что

при постоянном давлении и температуре. Это означает, что при этих условиях плотность газа определяется только его молярной массой. Такой результат позволяет ввести понятие относительной плотности одного газа по другому:

Эта величина показывает, во сколько раз первый газ тяжелее второго при одинаковых условиях.

3) Если реакция происходит в замкнутом сосуде (V = const) при постоянной температуре, то

Это соотношение означает, что в замкнутом сосуде при заданных условиях давление зависит только от общего числа молекул газов.

        Обобщая научно-учебную литературу, мы обратили внимание, что большинство работ предшествующих открытию обобщенного уравнения состояния идеального газа существовали на уровне гипотез, теоретических формулировок, экспериментальных наблюдений (гипотеза Авогадро, Тоунли, Пауэра, Броуна).

        В преддверии открытия обобщенного закона идет череда таких открытий, как законов Клапейрона, Гей-Люссака, Шарля, Бойля-Мариотта. Логическим завершением явилось обобщенное уравнение состояния идеального газа, открытое Дмитрием Ивановичем Менделеевым, в последствии получившее название – уравнение Клапейрона – Менделеева.

Глава 2. Анализ возможностей программы Flash 6

Flash 6 является продуктом как эволюционного, так и революционного развития. С помощью Flash 6 можно создавать все более и более ошеломляющую анимацию. Революцией явилось то, что теперь можно создать мультипликацию, которая легко может быть передана через Интернет в любой уголок мира. То, для чего требовались миллионы долларов и громадные студии, теперь можно создать на рабочем столе компьютера, а  созданный вами фильм в мгновение ока сможет обогнуть земной шар.

            Flash – это инструмент для создания анимации, и фильмы Flash могут восприниматься с помощью проигрывателя Flash. Однако важной особенностью Flash является то, что он дает возможность собрать вместе объекты, которые обычно требуют больших ресурсов, и превратить их в медиа -файлы, предназначенный для передачи по сети в составе Web-страницы. Flash специализируется на использовании векторной графики взамен растровой,  так как вместо описания каждого пикселя на экране векторы содержат достаточную информацию для воссоздания желаемого изображения. Например, растровая графика для линии между точкой А и точкой В будет содержать данные для всех промежуточных точек. Flash задаст только конечные точки. Кроме того, длинная линия и короткая линия будут порождать одинаковое количество информации, которую необходимо посылать через Интернет или хранить на домашнем компьютере, без потери качества изображения.

Flash – это приложение, предназначенное для создания фильмов. Файлы, создаваемые в Flash, - это мультфильмы, или просто фильмы(movie). А теперь представьте катушку пленки с обычным фильмом. Пленка состоит из множества маленьких рисунков, которые называются кадрами(frame). Кадры, просматриваемые один за другим, создают иллюзию движения. Иллюзию, потому что если увеличить скорость проектора, то движение станет быстрее, если уменьшить – медленнее.

В любом фильме объекты должны изменятся. Эти изменения могут быть весьма различными, а программа Flash поможет отобразить их на экране компьютера с наибольшей четкостью. Так, объекты могут изменять свое расположение на столе (в Flash вся работа с объектами происходит на столе(stage)). Они могут поменять свой цвет, форму, объем, прозрачность и видимость. Они могут издать звук или начать двигаться с другой скоростью. Движение – это основное изменение, которое происходит при анимации. Объект перемещается из пункта А в пункт Б, но прибудет он туда только двадцатью кадрами позже. Те кадры, где движение начинается и где оно заканчивается, в анимации называются   ключевыми кадрами(keyframes). Расстояние между ключевыми кадрами может быть большим или маленьким в зависимости от природы изменения (движения). Если ключевые изменения происходят в каждом кадре фильма, каждый кадр может быть назван ключевым.

В целом, программа Flash, созданная компанией Macromedia, представляет собой программное обеспечение, которое используется на самых современных Web-узлах. Когда вы путешествуете по Интернету, и посещаете Web-узлы, которые буквально полностью состоят из анимаций, или содержат кнопки, выполняющие занимательные эффекты, когда вы щелкаете на них, знайте, что, скорее всего, вы имеете дело с магией Flash.

Flash представляет мощную систему, предназначенную для создания анимационных файлов для Web-страниц. Обозначим некоторые возможности этой программы, т.е. назовем, что можно сделать в программе Flash:

1. Создать фильм Flash; для этого следует создать графические изображения, а затем анимировать их на протяжении определенного промежутка времени.
2. Использовать команду Flash, Publish (Публиковать), для преобразования фильма в воспроизводимый файл Flash. В то же время Flash создает исходный код HTML, который необходим для создания Web-страницы.
3. Добавить исходный код HTML в HTML-документ, который создает Web-страницу со ссылкой на воспроизводимый файл Flash. Этот процесс напоминает добавление графики на Web-страницу. Или можно использовать исходный код HTML для создания новой Web-страницы.
4. Загрузить новый или отредактированный документ HTML и воспроизводимый файл Flash в каталог, где хранятся все остальные файлы для ваших Web-страниц.
5. Открыть окно браузера, просмотреть свои Web-страницы и обнаружить на своей странице крутую анимационную картинку.

Для того чтобы просмотреть эффекты Flash, необходима программа просмотра. В настоящее время программы для просмотра файлов Flash установлены на многих компьютерных системах и браузерах, поэтому многие пользователи имеют возможность непосредственно просматривать Web-узлы, содержащие файлы Flash, без загрузки и установки какой-либо специальной программы. При отображении Web-узла, который содержит эффекты Flash,  система использует программу просмотра для проигрывания анимационных файлов Flash. Пользователи, которые не обладают встроенной программой просмотра файлов Flash, могут загрузить ее по адресу www.macromedia.com.

Web-узлы становятся все более и более сложными. Использование анимации и специальных эффектов выделят необходимый Web-узел среди множества обычных страниц. Добавить анимацию не сложно, для этого вам не придется становиться профессиональным художником. Каждый пользователь может создать простой анимационный файл для своего Web-узла, для этого лишь нужно немного времени.

В программе Flash 6 можно создать простой анимационный фильм, чтобы добавить его на свою Web-страницу. Можно создать готовую Web-страницу или узел и добавить в него текст, графику, интерактивные кнопки или анимацию.

Используя перечисленные и другие возможности программы Flash, авторы данной работы создали компьютерное моделирование физических процессов. Продуктом нашей работы является «Электронное пособие к разделу «Молекулярная физика».  

Глава 3. Моделирование физического эксперимента на компьютере.

Обобщив научную и научно-учебную литературу по молекулярно кинетической теории, мы перешли к физическому эксперименту (фото).

Для исследования мы выбрали три закона: закон Бойля-Мариота - изотермический процесс, закон Шарля (в отечественной литературе Гей-Люссака) – изобарный процесс и закон Клапейрона. В физическом кабинете  мы провели лабораторные работы с изменением некоторых параметров с целью дальнейшего введения исходного материала в компьютер.

Лабораторная работа № 1

Определение атмосферного давления с помощью закона Бойля-Мариотта.

Цель: Уметь рассчитывать атмосферное давление с помощью закона Бойля-Мариотта и производить необходимые для этого измерения.

Оборудование: мензурка с водой комнатной температуры, линейка, узкая стеклянная трубка, закрытая с одного конца, штатив с муфтой и лапкой.

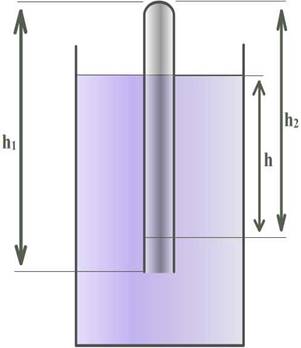1. Соберем установку как показано на рисунке.

Стеклянную трубку длиной h₁ опустим в мензурку с водой  закрытым концом вверх; проникшая в трубку вода сожмет имеющийся там столб воздуха до длинны h₂. Найдем чему равно атмосферное давление, если трубку погрузим на глубину h.

2. Измерим значения величин, необходимых для определения атмосферного давления, результаты измерений занесем в таблицу.

3. Выведем формулу расчета атмосферного давления с помощью закона Бойля – Мариотта.

Закон Бойля – Мариотта.

PV= const   при T=const, m=const

или

     (1)

         Так давление воздуха внутри пробирки после опускания её в воду (Р) компенсируется давлением столба жидкости высотой (h₁-h₂)  и давлением атмосферы (Р₀), то:

    (2)

Подставим уравнение (2) в (1) и решим:

  (3) 

4. Мы получили формулу для расчета атмосферного давления. Теперь используя данную формулу (3) произведем вычисления и заполним первую строку таблицы. Попробуем изменить один из параметров (h₂). Автоматически меняется  разность параметров (h₁-h₂). И измерения показывают изменение параметра h. Опять используя формулу (3), рассчитываем атмосферное давление и заполняем вторую и третью строки таблицы.

Мы получили практически одинаковые значения атмосферного давления, приблизительно равные 10⁵ Па. Что полностью соответствует показаниям барометра-анероида, находящегося в кабинете физики.

Лабораторная работа №2

Изучение процесса в газе при постоянном давлении.

Цель: Проверить опытным путем закон Шарля (в отечественной литературе закон Гей-Люссака)

Оборудование: Мензурка с водой комнатной температуры; мензурка с горячей водой; линейка; узкая стеклянная трубка, закрытая с одного конца (пробирка); пластилин; два штатива с муфтами и лапками; три термометра.

1. Изобарный процесс.

   при     и  

или

(4)

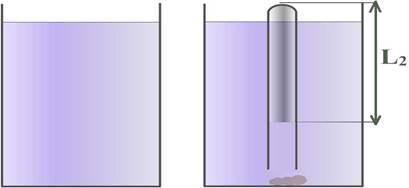
2. Проверим справедливость полученного равенства с помощью имеющегося оборудования. Для этого соберем установку как показано на рисунке.

2.1. Заполним одну из мензурок горячей водой, а другую водой комнатной температуры. Сверим показатели термометра, лежащего на столе, с показаниями термометра, опущенного в холодную воду. Значения этих температур должны быть одинаковы. Горячая вода должна наполнять более двух третьих от объема мензурки. Теперь опустим пробирку открытым концом вверх в горячую воду и будем прогревать воздух в пробирке в течение трех-пяти минут. Поместим резервуар третьего термометра и измерим температуру прогретого воздуха в  ⁰С, переведем в К.

 Занесем в таблицу значение начальных параметров прогретого воздуха: T₁ и V₁, а точнее L₁ (высота пробирки).

2.2. Замажем  пластилином открытый конец прогретой пробирки. Перевернем и опустим эту пробирку в мензурку с водой комнатной температуры.  Под водой снимем пластилин и погрузим пробирку как можно глубже в воду, пробирка частично заполнится водой так, как воздух в пробирке охладится и займет меньший объем. При этом два параметра поменяют свои значения: T₁→T₂; V₁→V₂.

Давление воздуха внутри пробирки останется неизменным. Измерим длину охлажденного столба воздуха в пробирке (L₂). Занесем параметры T₂  и V₂, а точнее L₂ в таблицу. Напомним, что температура T₂ это комнатная температура в К (показания второго термометра).               

Получим первую строку таблицы. Увеличим температуру горячей воды и, следственно, температуру прогретого воздуха в пробирке, повторим эксперимент. Таким образом, заполним вторую и третью строку таблицы.

         Из равенства      1, дальнейшие расчеты показывают, что все три равенства справедливы. Таким образом, мы подтвердили равенство (4). И  пришли к выводу, что при постоянном давлении отношение объема газа к абсолютной температуре остается неизменным.

Лабораторная работа №3

Экспериментальное подтверждение закона Клапейрона.

Цель: Проверить лабораторным путем справедливость объединенного газового закона - закона Клапейрона.

Оборудование: Мензурка с водой комнатной температуры; мензурка с горячей водой; линейка; узкая стеклянная трубка, закрытая с одного конца (пробирка); пластилин; два штатива с муфтами и лапками; три термометра.

1.  при

или

(5)

2. Соберем установку как показано на рисунке.

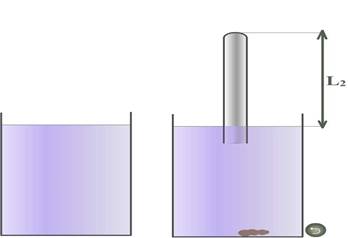
3. Наполним одну мензурку водой комнатной температуры, вторую мензурку горячей водой, так, что бы при опускании пробирки в мензурки вода не выливалась через край. Сверим показания первого и второго термометра. Они должны быть одинаковы. Напомним, что первый показывает температуру воздуха в кабинете физики, а второй - температуру холодной воды.

         Опустим пробирку в горячую воду закрытым концом вниз и прогреем воздух в пробирке. Измерим температуру воздуха в пробирке в ⁰С, переведем в Кельвины и занесем в таблицу. Закроем открытый конец пробирки пластилином, перевернем и очень медленно и аккуратно опустим в мензурку с холодной водой на минимальную глубину. Практически у поверхности, под водой  снимем пластилин. Некоторая часть воды заполнит трубку. Уровень воды в пробирке и уровень поверхности воды в мензурке должны совпадать.

В этом эксперименте меняются все три параметра: температура воздуха в пробирке понижается T₁=>T₂; объем в воздуха в трубке уменьшается V₁=>V₂ и следовательно L₁=>L₂; давление понизилось P₁=>P₂.

4. Заполним первую строчку таблицы. Изменим температуру горячей воды, повторим эксперимент дважды и заполним вторую и третью строки таблицы. Отметим, эксперименты мы проводим трижды для составления программы моделирования физических процессов на компьютере.

Принимаем во внимание, что L₂=L₁-h; P₁ = Pатмосфер. 101325 Па 10⁵ Па; P₂ = P_{атмосфер.}-gh;  = 1000 кг/м³;  g  10 м/c²

Теперь проверим равенство

         Дальнейшие расчеты показывают, что два других равенства тоже справедливы. На основе полученных результатов можно сделать вывод, что при быстром и аккуратном выполнении эксперимента мы полностью подтверждаем справедливость закона Клапейрона. Быстрота эксперимента целесообразна для уменьшения потерь теплоты горячей водой.

         При создании компьютерного пособия было написано более двадцати скриптов - небольших программ. Пользовательские скрипты выполняются на компьютере посредством вызова определенных команд, которые обозначены в фрагментах кода обыкновенной веб-страницы. Для того чтобы они могли быть выполнены, браузер должен уметь поддерживать язык, на котором скрипты написаны. Наши скрипты были написаны на Actionscript.

Наиболее значимые приведем ниже.

Лабораторная работа №1

on (release) {

                _root.win.lab1.windial._visible = false;

                _root.win.lab1.h2_win = _root.win.lab1.windial.sel_list.getValue();

                _root.win.lab1.h1_h2 = 0.6-_root.win.lab1.h2_win;

                _root.win.lab1.h = (100000*_root.win.lab1.h1_h2)/(10000*_root.win.lab1.h2_win);

                _root.win.lab1.P0 = (10000*_root.win.lab1.h*_root.win.lab1.h2_win)/(_root.win.lab1.h1_h2);

}

Лабораторная работа №2

on (release) {

                _root.win.lab2.t1s = _root.win.lab2.wincon.sel_list.getvalue();

                _root.win.lab2.t1g = _root.win.lab2.t1s + 273;

                _root.win.lab2.L2 = (301/_root.win.lab2.t1g)*0.6;

                _root.win.lab2.wincon._visible = false;

Заключение

         Трудно переоценить роль информационных технологий в развитии современного образования. В настоящее время компьютер является одним из самых мощных и эффективных технических средств, используемых не только на уроках информатики, но и на уроках физики, биологии, истории и т.д.

         Многие явления и процессы, изучаемые в условиях школьного кабинета физики невозможно продемонстрировать традиционным путем: явления микромира, быстро протекающие процессы, ядерные реакции и т.д. Использование персонального компьютера позволяет повысить наглядность при изучении физических процессов.

         Мы поставили своей целью создать электронное пособие к разделу «Молекулярная физика» пригодное для изучения процессов в газах на уроке физики. Для этого мы обобщили научно-учебную литературу по термодинамике, статистической физике и статистической термодинамике. Следующим шагом проанализировали возможности программы Flash, с помощью которой создали впоследствии электронное пособие. Далее провели экспериментальные исследования с помощью физического оборудования в кабинете физики. За основу мы взяли три лабораторные работы. Причем, при выполнении каждой работы, мы трижды повторяли эксперименты, изменяя предварительно некоторые параметры. Эти действия были необходимы для написания компьютерных программ и компьютерного моделирования.

В результате авторы создали электронное пособие или информационную модель.  В общем виде информационные модели представляют собой объекты и процессы в образной и знаковой форме. В нашей  работе представлены в основном динамические информационные модели – модели,  описывающие процессы изменения и развития систем, и компьютерные эксперименты. Формы представления: текст, в том числе и сменяющийся; анимации; таблицы с изменением параметров и результатов.

В итоге мы создали  электронное пособие к разделу  «Молекулярная физика»,  включающее в себя теоретическую и практическую части. Практическая часть включает в себя возможность выполнения на компьютере трех  лабораторных работ.

Пособие целиком  и  полностью отвечает ранее обозначенным требованиям:

1.     Пособие размещается на диске CD-R – очень компактно.

2.     Содержит теоретический и практический материал. Причем, учащийся может обращаться к той или иной части пособия в любое время работы.

3.     Во всех трех лабораторных работах можно изменять исходные параметры и получать соответствующие результаты.

4.     Пособие предназначено для использования на уроках физики и на индивидуальных занятиях, а также может использоваться при самостоятельном изучении данной темы учеником.

5.     Пособие доступно в использовании и рассчитано даже на учащегося, имеющего поверхностные знания о компьютере (простота и доступность). 

Пособие учитывает индивидуальные особенности восприятия текста и визуальной информации с монитора (кнопки перехода). В практической части информация появляется последовательно. Текстовые эпизоды чередуются с компьютерной анимацией и моделированием. Такое чередование информации не напрягает зрение.

         Есть еще одно несомненное достоинство данной работы. Пособие позволяет провести все три лабораторные работы в течение одного урока, т.к. применяется аналогичное оборудование (виртуальное и физическое). Это очень актуально при наличии лимита времени, отводимого на изучение курса физики в нашей гимназии.

         Авторы данной работы надеются, что учитель и учащиеся, будут с удовольствием работать с нашим электронным пособием. Процесс обучения станет более наглядным, понятным, комфортным и интересным.

Список литературы

1.     Голин Г.М, Хрестоматия по истории физики. Классическая физика./ Сост. Г.М. Голин.- Мн.: Выш. Школа,1979.-272с.

2.     Громов С.В. Физика: Оптика. Тепловые явления. Строение и свойства вещества: Учебник для 11кл. общеобразовательных учреждений / С.В.Громов; Под ред. Н.В.Шароновой.- 3-е изд.- М.:Просвещение,2002.-287с.

3.     Детская энциклопедия. Вещество и энергия. / Сост.: А.И. Маркушевич, Б.А. Воронцов-Вельяминов, Е.М. Тяжельников и  др.; Под ред. И.В.Петрянов.-М.:Педагогика,1991.-336с.

4.     Касьянов В.А. Физика: Учеб для 10 кл.-М.:Дрофа,2000.-416с.

5.     Мякишев Г.Я. Физика: Учеб.  для 10 кл. общеобразовательных учреждений/ Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский.-12-е изд.- М.:Просвещение,2004.-336с. 

6.     Мякишев Г.Я., Буховцев Б.Б. Физика: Учебник для 10 кл.- М.: Просвещение, 1990.-223с.

7.     Сандерс Б. Эффективная работа: Flash 5 – СПб: Питер, 2002 – 352с.

8.     Угринович Н.Д. Информатика и информационные технологии. Учебник для 10-11 классов / Н.Д. Угринович. – М.: Бином. Лаборатория знаний, 2003. – 512с.: ил.

9.     Физика: Учеб. для 10 класс школ и классов с углубленным изучением физики/ О.Ф. Кабардин, В.А.Орлов, Э.Е. Эвенчик и др.; Под ред. А.А. Пинского.- 6-е изд.-М.:Просвещение,2001.-415с.

10. Физика Справочник школьника \ Сост. Т. Фещенко, В. Вожегова; Под ред. А.Барашкова.-М.:Слово,1995.-575с.

11. Хрестоматия по физике: Учеб. пособие для учащихся/ Сост: А.С Енохович, О.Ф. Кабардим, Ю.А. Коварский и др.; Под ред. Б.И.Спасского.-М.:Просвещение,1982.-223с.

12. Энциклопедический словарь юного физика/ Сост. В.А Чуянов.- 2-ое изд., исправлен и дополнен – М.: Педагогика, 1973.-545с.