Методическая разработка урока "Формулы приведения тригонометрических функций"

План урока

преподавателя – Мачалиной Натальи Ивановны.

по учебной дисциплине – математика.

Дата проведения занятия: 7 февраля 2019 г.

Группа: М – 18 – 12.

Время, отведенное на занятие: 90 минут.

Тема урока: формулы приведения тригонометрических функций.

Тип урока: изучения и первичного закрепления новых знаний.

Форма обучения: классно-урочная.

Форма деятельности: фронтальная и индивидуальная.

Цель урока: формирование знаний и умений в применение формул приведения тригонометрических функций.

Задачи урока:

1. Образовательные:

- ознакомить с формулами приведения тригонометрических функций, показать их применение при преобразовании тригонометрических выражений;

- сформировать знания и умения в применение формул приведения тригонометрических функций при преобразовании тригонометрических выражений;

- обеспечить в ходе урока обучение правильному применению формул приведения тригонометрических функций и таблицы значений тригонометрических функций.

2. Развивающие:

- способствовать развитию у обучающихся умений анализировать, устанавливать связи, причины и следствия;

- предвидеть возможные ошибки и способы их устранения;

- способствовать повышению концентрации внимания, развитию у студентов памяти и речи.

3. Воспитательные:

- способствовать развитию интереса к предмету «Математика»;

- способствовать развитию самостоятельности мышления;

- способствовать формированию нравственных качеств личности (уверенность в себе, целеустремленность).

Методы обучения: словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО); практические методы.

Оборудование: компьютер, проектор, раздаточный материал.

Дидактическая структура урока	Содержание	Методическая структура урока			Признаки решения дидактических задач
Дидактическая структура урока	Содержание	Методы обучения	Форма деятельности	Средства обучения	Признаки решения дидактических задач
Организационный момент	- приветствие; - определение цели и задач урока.	словесные методы	фронтальная		Студенты готовы к занятию
Актуализация знаний	Вопросы к группе: - какие тригонометрические функции вы уже знаете? - что называется синусом острого угла прямоугольного треугольника? - что называется косинусом острого угла прямоугольного треугольника? - что называется тангенсом острого угла прямоугольного треугольника? - что называется котангенсом острого угла прямоугольного треугольника?	словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО)	фронтальная	компьютер, проектор, слайды с вопросами	Студенты отвечают на вопросы
Сообщение нового материала	Ознакомить с формулами приведения тригонометрических, показать правило для записи формул приведения. Дать таблицу "Формулы приведения тригонометрических функций аргументов ". Показать применение формул приведения тригонометрических функций при преобразование тригонометрических выражений.	словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО); практические методы.	фронтальная и индивидуальная	компьютер, проектор, слайды с формулами приведения тригонометрических функций	Студенты: - воспринимают материал; - применяют формулы приведения тригонометрических функций при преобразование тригонометрических выражений; - сравнивая решения с образцами, самостоятельно обнаруживают ошибки и корректируют решение.
Закрепление изученного материала	Самостоятельная работа обучающихся по теме урока	словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО); практические методы.	фронтальная и индивидуальная	раздаточный материал	Студенты выполняют самостоятельную работу
Подведение итогов, рефлексия	Педагог анализирует и оценивает успешность выполнения поставленных задач. Педагог просит обучающихся оценить урок с помощью карточек трёх цветов: «красная» - «отлично», «зелёная» - «хорошо», «синяя» - «удовлетворительно».	словесные методы	фронтальная, индивидуальная	карточки трёх цветов	Обучающиеся оценивают урок
Домашнее задание	Выполнить дома следующие задания: - выучить формулы преобразования тригонометрических функций; - выучить правила для записи формул. - выполнить задания из учебника: - № 9 (все четные номера); - № 10 (1).	словесные методы (рассказ, объяснение); наглядные методы (демонстрация, ТСО).	фронтальная	компьютер, проектор, слайды с заданиями	Студенты записывают домашнее задание

План - конспект

Формулы приведения

С помощью формул приведения осуществляется преобразование выражений вида: , nZ.

Правило для записи формул приведения:

1) перед приведённой функцией ставится тот знак, который имеет исходная функция, если (рис.4);

2) функция меняется на «кофункцию», если n нечётно, функция не меняется, если n чётно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.).

Формулы приведения тригонометрических функций аргументов .

Функция.	Аргумент

Упражнения с решениями.

Пример 1. Упростите выражение

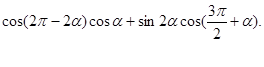
Решение. Так как по формулам приведения и то

Пример 2. Вычислите 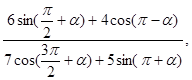если

Решение. Используя формулы приведения, преобразуем числитель и знаменатель:

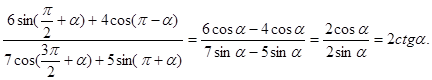
Если , то .

Ответ: 2.

Пример 3. Вычислите

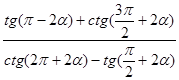,если .

Решение. По формулам приведения

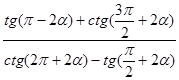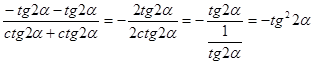Если , то .

Ответ:-3.

Самостоятельная работа

Вариант № 1.

1. Упростите выражение

2. Вычислите

, если .

3. Докажите тождество

4. Вычислите

, если .

Самостоятельная работа

Вариант № 2.

1. Упростите выражение

2. Вычислите

, если .

3. Докажите тождество

4. Вычислите

, если .

План урока преподавателя –

Дидактическая структура урока

Показать применение формул приведения тригонометрических функций при преобразование тригонометрических выражений

Домашнее задание Выполнить дома следующие задания: - выучить формулы преобразования тригонометрических функций; - выучить правила для записи формул

Решение . Так как по формулам приведения и то

Если , то . Ответ:-3.

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

08.01.2022