Функция. Производная. Первообразная. 

Пример 1

На рисунке изображены график функции y=f(x) и девять точек на оси абсцисс: х₁,х₂,х₃,...,х₉.В скольких из этих точек производная функции f(x) положительна.  

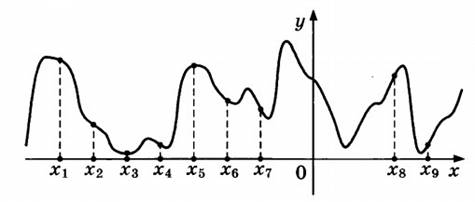
Решение:

Вспомним о связи между характером монотонности функции и знаком ее производной. Если функция возрастает на промежутке и имеет на нем производную, то производная неотрицательна. Рассмотрим промежутки возрастания функции. Получим 2 точки.

Ответ: 2

Пример 2

На рисунке изображен график функции y=f(x) и отмечены точки -7, -3, 3, 7. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

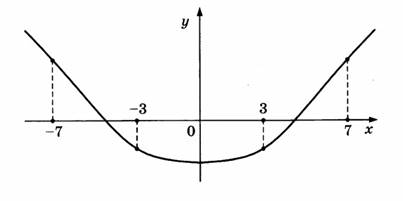
Решение:

Вспомним о связи между характером монотонности функции и знаком ее производной. Если функция возрастает на промежутке и имеет на нем производную, то производная неотрицательна. Функция возрастает на промежутке [0;+∞). Точки 3 и 7 принадлежат этому промежутку. В точке 7 значение производной наибольшее. Ответ: 7

 3

 изображены график функции у = f ′( )x - производной функции

f(x), и семь точек на оси абсцисс: х₁,х₂,х₃,...,х₇.В скольких из этих точек функции возрастает.  

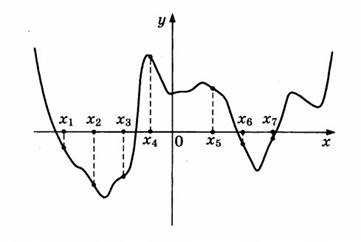
Решение:

Вспомним, как по знаку производной можно установить характер монотонности функции. 

Если во всех точках открытого промежутка Х выполняется неравенство ^{f ′( )x ≥ 0} (причем равенство ^{f ′( )x = 0} либо не выполняется, либо

выполняется в конечном множестве точек), то функция  ^{y=f(x)возрастает} на промежутке Х.

Рассмотрим промежутки, где производная принимает положительные значения. Получим 2 точки.

Ответ: 2

 4

На  изображены график функции у = f ′( )x - производной функции f(x), и семь точек на оси абсцисс: х₁,х₂,х₃,...,х₇.В скольких из этих точек функции убывает.

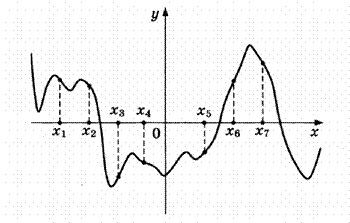
Решение:

Вспомним, как по знаку производной можно установить характер монотонности функции. 

Если во всех точках открытого промежутка Х выполняется неравенство ^{f ′( )x ≤ 0} (причем равенство ^{f ′( )x = 0} либо не выполняется, либо

выполняется в конечном множестве точек), то функция  ^{y=f(x)убывает} на промежутке Х.

Рассмотрим промежутки, где производная принимает отрицательные значения. Получим 3 точки.

Ответ: 3

Пример 5

Прямая у =8х +11 параллельна касательной к графику функции у = х² +7х + 7 . Найдите абсциссу точки касания.

Решение:

Касательная к графику функции у = х² +7х + 7 параллельна прямой у =8х +11.

Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой. k_kac =8. Но k_kac = f ′( )a , где а

– точка касания.

Найдем производную данной функции f ′( )х = 2х + 7

2а + 7 = 8; 2а =1; а = 0,5;

Ответ: 0,5

 6

 изображен график функции y=f(x) и касательная к нему в точке с

абсциссой х₀. Найдите значение производной в точке функции f(x)  

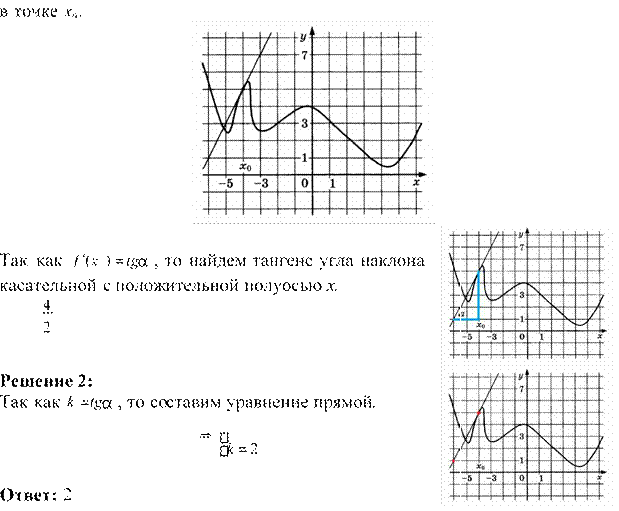Решение 1: 

0

tgα=      = 2

Ответ: 2

− 4k + m = 5 − 4k + m = 5 m =13

                     ⇒

−6k + m =1 2k = 4 y=2x+13

 7

Прямая у = 7х −9является касательной к графику функции у = ах² −17х +3. Найдите a.

Решение:

Составим уравнение касательной к графику функции у = ах² −17х +3.

_1.     Найдем производную данной функции f ′( )х = 2ах −17

_2.     Найдем значение производной в точке х₀. ^{f ′(x0) = 2ax0 −17}

_3.     Найдем значение функции в точке х₀ . ^{f x( 0) = ax02 −17x0 + 3}

_4.     Составим уравнение касательной ^{y = f ′(x0)(x − x0) + f (x0)}, получим y = (2ax0 −17)(x − x0) + ax02 −17x0 + 3. Затем преобразуем уравнение, раскрыв

скобки. y = 2ax₀x − 2ax₀² −17x +17x₀ + ax₀² −17x₀ + 3 = (2ax₀ −17)x − ax₀² + 3

2ax₀ −17=7

Получим систему:           ₂                    

3−ax₀ =−9

x₀ =1

Решив эту систему, получим           

a =12

Ответ: 12

Пример 8

Материальная точка движется прямолинейно по закону х( )t = −t² + 5t + 23, где х – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t =1 с.  

Решение:

_1.                      Найдем производную функции x(t), х′( )t = −t +5

_2.                      Найдем значение производной в точке t=1,  ^{х′(1) = −1+5 = 4} Ответ: 4

 9

рисунке изображены график функции у = f ′( )x - производной функции

f(x). Найдите абсциссу точки, в которой касательная к графику у = f(x) параллельна прямой у=3х или совпадает  ней. 

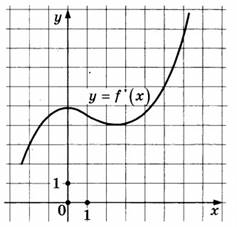
Решение:

Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой. k_kac = 3. Но k_kac = f ′( )a , где а

– точка касания. Значит, а = -2

Ответ: -2

Пример 10

На рисунке изображены график функции у = f ′( )x - производной функции f(x). Найдите абсциссу точки, в которой касательная к графику у = f(x) параллельна оси абсцисс или совпадает  ней.

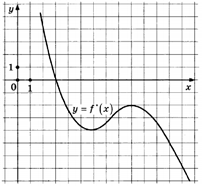
Решение:

Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой. k_kac = 0. Но k_kac = f ′( )a , где а – точка касания . Значит, а = 3 Ответ: 3

 11

рисунке изображены график первообразной у = F(x) некоторой функции у = f ( )x , определенной на интервале (2; 13). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [4; 12].

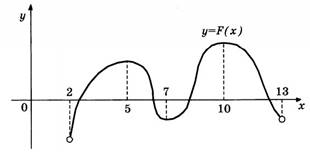
Решение:

Функция у = f ( )x - производная для функции у = F(x). Другими словами, дана функция, необходимо найти в каких точках производная этой функции равно нулю. 

Воспользуемся теоремой: Если функция у = f ( )^x имеет экстремум в точке ^{х = х0}, то в этой точке производная функции либо равна нулю, либо не

существует. 

На отрезке [4; 12] функция имеет три экстремума. Следовательно, уравнение f(x)=0  имеет три решения.

Ответ: 3

 12 рисунке изображен график некоторой функции y=f(x). Одна из первообразных этой функции равна F( )x =  x³ − x² + 3x + 2. Найдите площадь заштрихованной фигуры.

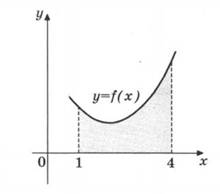
Решение:

b

S = ∫ f ( )x dx = F( )b − F( )a , где F(x) – первообразная  для f(x)

a

          b                                  4                            1 ^{3              2}                             4         1     ^{3            2}                                         1

S = ∫ f x dx( ) = ∫ f x( ) = x − x +3x + 2                    =            ⋅4 − 4 +3⋅4+ 2−(       −1+3+ 2) =

                                                    6                                6                                  6

          a                                 ₁                                                                                 1

Ответ: 4,5