Подготовка к ЕГЭ математика профильный уровень. Тема "Вероятность"

Задание 4 (базовый уровень, время – 3 мин.)

Тема: Простейшие задачи теории вероятностей.

Что проверяется:

  Умение строить и исследовать простейшие математические модели.

Что нужно знать и уметь:

  Уметь моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.  Классическое определение вероятности:

Вероятностью события А при проведении некоторого испытания называют отношение числа тех исходов, в результате которых наступает событие А, к общему числу всех (равновозможных между собой) исходов этого испытания.

где P(A) – вероятность случайного события А;

      N(A) – количество тех исходов, в которых наступает событие А;       N – число всех возможных исходов данного испытания.

        Помнить, что                      .

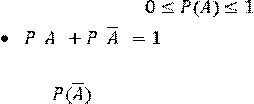где P(A) – вероятность наступления события А;        – вероятность наступления события  (события противоположного А, т.е. наступающего в том и только в том случае, когда не наступает событие А).  Правило умножения:

Для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.

 События А и В называют несовместными, если они не могут происходить одновременно.

Несовместные события изображаются непересекающимися подмножествами множества всех исходов испытания.

Если А и В несовместны, то вероятность того, что наступит или А, или В, равна P(A + B) = P(A) + P(B). 

  Произведением событий А и В называют событие, которое наступает тогда и только тогда, когда наступает и событие А, и событие В. Обозначается А·В или АВ.

  Сумма вероятностей двух событий равна сумме вероятности произведения этих событий и вероятности суммы этих событий.

  События А и В называют независимыми, если вероятность их произведения равна произведению вероятностей этих событий:

P(AB) = P(A)P(B).

Вероятность суммы двух независимых событий равна разности суммы вероятностей этих событий и произведения вероятностей этих событий: P(A+B) = P(A) + P(B) – P(A)P(B)  Произведение подряд идущих первых n натуральных чисел обозначают n! и называют «эн факториал»:

n! = 1 · 2 · 3 · … · (n – 2) · (n – 1) · n.

  n различных элементов можно расставить по одному на n различных мест ровно n! способами:

P_n = n!

  Число всех выборов k элементов из n данных без учета порядка называют числом сочетаний из n элементов по k и обозначают :

  Число всех выборов k элементов из n данных с учетом их порядка называют числом размещений из n элементов по k и обозначают :