Построение графиков сложных функций на основе свойства монотонности.

ПРОЕКТ

на тему: «Некоторые задачи II части ОГЭ по математике»

2018 год

 

                                               Введение.

Определение проблемы: необходимость разобрать  решения сложных задач второй части экзаменационной работы.

Задачи исследования: изучение методов решения некоторых сложных, наиболее часто встречающихся, видов школьных математических задач из II части тестов ОГЭ; рассмотрение структуры процесса решения задач; развитие умений самостоятельно конструировать свои знания; ориентироваться в информационном и социальном пространстве.

Гипотеза: применение разнообразных форм работы, развитие умения составлять формулы зависимостей между математическими величинами на основе обобщения частных случаев.

Обсуждение методов исследования.

- Метод конкретных ситуаций (совместное обсуждение методов решения задачи под руководством преподавателя, следование принципу «процесс обсуждения важнее самого решения», самостоятельное изучение и подготовленное в письменном виде решение сложной задачи)

Результаты исследования.

- Сбор, систематизация полученной информации в виде решенных задач, корректировка

Анализ полученных данных.

- Оформление результатов исследовательской работы в электронном виде

Вывод:

- При решении систем уравнений второй степени целесообразно применять метод подстановки;

- При решении текстовых задач важно правильно ввести переменную и составить формулу зависимости между величинами;

- При решении геометрических задач внимательно анализировать условие задачи, находить взаимосвязь между элементами геометрических фигур, применять разные методы решения задачи.

 

 

 

 

 

Практическая часть.

 

       Задания типа № 21.

 

№1. Решите си­сте­му уравнений:

 

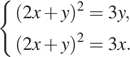
Решение.

Последовательно получаем:

 

 

 

       Ответ: (0; 0); (; ).

     

 

№2. Со­кра­ти­те дробь

 

 

Решение.

Сгруппируем и вынесем общий множитель:

 

Ответ:   .

 

№3. Ре­ши­те си­сте­му урав­не­ний

 

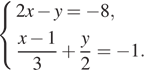
Решение.

Выразим y из пер­во­го урав­не­ния и под­ста­вим во второе, пред­ва­ри­тель­но умно­жив обе его части на 6:

 

 

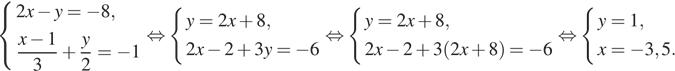
Ответ: (−3,5; 1).

 

 

 

 

№4.  Решите си­сте­му урав­не­ний  

 

 

 

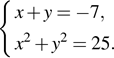
Решение.

Из пер­во­го урав­не­ния си­сте­мы выразим:  . Под­ста­вим по­лу­чен­ное вы­ра­же­ние во вто­рое урав­не­ние системы, получаем

   

       D = b² – 4ac

       D = 7² - 4 = 49 – 48 = 1

       х₁ = - 4, х₂ = - 3

Вычислим значение у₁ и у₂:

      у₁ = - (-4) – 7 = - 3

       у₂= - (-3) – 7 = - 4

     

Таким образом, ре­ше­ние ис­ход­ной си­сте­мы  .

Ответ:  .

 

                      Задания типа № 22.

 

№1. Рас­сто­я­ние между двумя при­ста­ня­ми по реке равно 80 км. Катер прошёл от одной при­ста­ни до дру­гой, сде­лал сто­ян­ку на 1 ч 20 мин и вер­нул­ся об­рат­но. Всё пу­те­ше­ствие за­ня­ло Най­ди­те ско­рость те­че­ния реки, если из­вест­но, что ско­рость ка­те­ра в сто­я­чей воде равна 18 км/ч.

Решение.

Пусть ско­рость те­че­ния реки равна  км/ч. Тогда ско­рость ка­те­ра по те­че­нию реки равна (18 + х) км/ч, а про­тив те­че­ния (18 – х) км/ч. Время дви­же­ния ка­те­ра от одной при­ста­ни до дру­гой по те­че­нию реки равно , а про­тив те­че­ния  . Весь путь занял   -  = 9 ч. Со­ста­вим уравнение:

 

 

Корень −2 не удовлетворяет условию задачи. Ско­рость те­че­ния реки равна 2 км/ч.

 

Ответ: 2 км/ч.

 

№2. На пост главы ад­ми­ни­стра­ции го­ро­да пре­тен­до­ва­ло три кан­ди­да­та: Ан­дре­ев, Бо­ри­сов, Ва­си­льев. Во время вы­бо­ров за Ва­си­лье­ва было от­да­но в 1,5 раза боль­ше го­ло­сов, чем за Ан­дре­ева, а за Бо­ри­со­ва — в 4 раза боль­ше, чем за Ан­дре­ева и Ва­си­лье­ва вме­сте. Сколь­ко про­цен­тов го­ло­сов было от­да­но за по­бе­ди­те­ля?

Решение.

Заметим, что по­бе­ди­те­лем на вы­бо­рах ока­жет­ся Борисов. Пусть ко­ли­че­ство голосов, от­дан­ных за Борисова, равно х. Тогда за Ан­дре­ева и Ва­си­лье­ва вме­сте от­да­ли    . Про­цент голосов, от­дан­ных за Бо­ри­со­ва   х : (х +  ) × 100 = 80%.

 

Ответ: 80%.

 

№3. Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 33 минуты раньше, чем велосипедист приехал в А, а встретились они через 22 минуты после выезда. Сколько часов затратил на путь из В в А велосипедист?

Решение.

Пусть  — ско­рость мотоциклиста,  — ско­рость велосипедиста. При­мем рас­сто­я­ние между го­ро­да­ми за единицу. Мо­то­цик­лист и ве­ло­си­пе­дист встре­ти­лись через 22 минуты, то есть через  часа, после выезда, по­это­му Мо­то­цик­лист при­был в B на 33 минуты раньше, чем ве­ло­си­пе­дист в А, от­ку­да  По­лу­ча­ем си­сте­му уравнений:

 

 

 

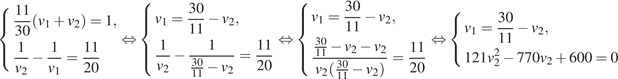
Скорость мо­то­цик­ли­ста не может быть отрицательной, по­это­му ско­рость ве­ло­си­пе­ди­ста равна    , а время, за­тра­чен­ное на весь путь равно 

 

Ответ: 1,1.

 

№4. Игорь и Паша кра­сят забор за 18 часов. Паша и Во­ло­дя кра­сят этот же забор за 20 часов, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко минут маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

Решение.

За один час Игорь и Паша кра­сят 1/18 забора, Паша и Во­ло­дя кра­сят 1/20 забора, а Во­ло­дя и Игорь — за 1/30 забора. Ра­бо­тая вместе, за один час два Игоря, Паши и Во­ло­ди по­кра­си­ли бы:

 

  забора.

 

Тем самым, они могли бы по­кра­сить один забор за 7,2 часа. По­сколь­ку каж­дый из маль­чи­ков был учтен два раза, в ре­аль­но­сти Игорь, Паша и Во­ло­дя могут по­кра­сить забор за 14,4 часа=864 минуты. Ответ: 864

 

                                        Задания типа № 23.

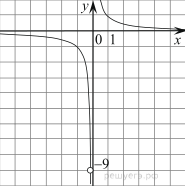№1. Постройте график функции y =   . Определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.

Решение.

Упростим вы­ра­же­ние для функции:

 

  при .

 

Таким образом, получили, что гра­фик нашей функ­ции сво­дит­ся к гра­фи­ку функ­ции y =   с вы­ко­ло­той точ­кой (-; -9).

Построим гра­фик функ­ции (см. рисунок).

 

 

 

Заметим, что пря­мая y = kx  про­хо­дит через на­ча­ло ко­ор­ди­нат и будет иметь с гра­фи­ком функ­ции ровно одну общую точку толь­ко тогда, когда будет про­хо­дить через вы­ко­ло­тую точку (-; -9). Под­ста­вим ко­ор­ди­на­ты этой точки в урав­не­ние пря­мой и найдём ко­эф­фи­ци­ент k.

 Ответ: 81.

 

№2. Из­вест­но, что гра­фи­ки функ­ций y = x² + p и y = 4x – 5 имеют ровно одну общую точку. Опре­де­ли­те ко­ор­ди­на­ты этой точки. По­строй­те гра­фи­ки за­дан­ных функ­ций в одной си­сте­ме ко­ор­ди­нат.

Решение.

Найдём абс­цис­сы точек пересечения:

 

 

Графики функций, будут иметь ровно одну точку пересечения, если это урав­не­ние имеет ровно одно решение. То есть, если дис­кри­ми­нант этого квад­рат­но­го урав­не­ния будет равен нулю.

 

 

Подставив па­ра­метр p в урав­не­ние, найдём x ко­ор­ди­на­ту точки пе­ре­се­че­ния этих функций:

 

Координата y на­хо­дит­ся от­ту­да же путём под­ста­нов­ки ко­ор­ди­на­ты x в любое из уравнений, например, во второе:   

 

Теперь, зная p можем по­стро­ить гра­фи­ки обеих функ­ций (см. рисунок).

 

 

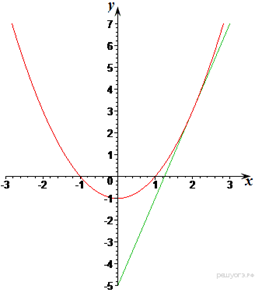
 Ответ: (2; 3)

 

 

 

 

 

 

 

 

 

 

 

 

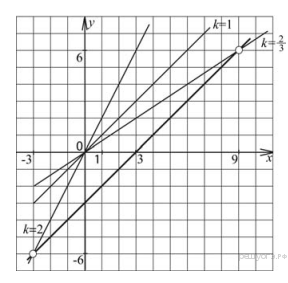
№3.

 

 

 

Постройте гра­фик функ­ции y =    и определите, при каких зна­че­ни­ях k по­стро­ен­ный гра­фик не будет иметь общих точек с пря­мой y = kx.

Решение.

Преобразуем функцию: y =  при x ≠ -3 и  x ≠ 9 . Гра­фик — пря­мая y = x – 3 без двух точек (-3; -6) и (9; 6). Пря­мая y = kx  не будет иметь с по­стро­ен­ной пря­мой общих точек, если она будет ей параллельна, т. е. при k = 1 , и если она будет про­хо­дить через вы­ко­ло­тые точки. Через первую из этих точек пря­мая y = kx проходит, если k = 2, а через вто­рую — если k = .

Ответ: 

 

№4. Постройте гра­фик функ­ции  и определите, при каких зна­че­ни­ях па­ра­мет­ра a он имеет ровно две общие точки с пря­мой y = a.

 

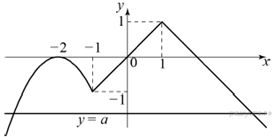Решение.

Построим гра­фик функ­ции y = −x² − 4x − 4 на про­ме­жут­ке (−∞; −1), гра­фик функ­ции y = x на про­ме­жут­ке [−1; 1] и гра­фик функ­ции y = 2 − x на про­ме­жут­ке (1; +∞).

 

Прямая y = a имеет с по­стро­ен­ным гра­фи­ком ровно две общие точки при a < −1 и при 0 < a < 1.

 

Ответ: a < −1, 0 < a < 1.

 

Задания типа № 24.

№1. Сто­ро­ны AC, AB, BC тре­уголь­ни­ка ABC равны 2,   и 2 со­от­вет­ствен­но. Точка K рас­по­ло­же­на вне тре­уголь­ни­ка ABC , причём от­ре­зок KC пе­ре­се­ка­ет сто­ро­ну AB в точке, от­лич­ной от B. Из­вест­но, что тре­уголь­ник с вер­ши­на­ми K, A и C по­до­бен ис­ход­но­му. Най­ди­те ко­си­нус угла AKC, если ∠KAC > 90°.

Решение.

Рассмотрим по­доб­ные тре­уголь­ни­ки ABC и AKC и уста­но­вим со­от­вет­ствие между их углами. Про­тив боль­шей сто­ро­ны все­гда лежит боль­ший угол, в тре­уголь­ни­ке ABC это угол ABC в тре­уголь­ни­ке , в свою очередь, есть тупой угол  и он яв­ля­ет­ся наибольшим, зна­чит∠КАС = ∠АВС.  Угол АСК за­ве­до­мо не может быть равен углу  так как он со­став­ля­ет толь­ко его часть. Сле­до­ва­тель­но угол АСВ равен углу АКС.

Найдём ко­си­нус угла  ис­поль­зуя тео­ре­му косинусов:

 

 

 

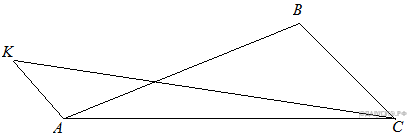
Ответ: 

 

№2.    Прямая, па­рал­лель­ная ос­но­ва­ни­ям  и  тра­пе­ции , про­хо­дит через точку пе­ре­се­че­ния диа­го­на­лей тра­пе­ции и пе­ре­се­ка­ет её бо­ко­вые сто­ро­ны  и  в точ­ках  и  соответственно. Най­ди­те длину от­рез­ка , если , .

Решение.

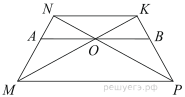
1)  по двум углам:

а)  как вертикальные;

б)  как внут­рен­ние на­крест ле­жа­щие углы при  и се­ку­щей .

 

 

2)  по двум углам:

а)  — общий;

б)  как со­от­вет­ствен­ные при  и се­ку­щей .

 

3) ана­ло­ги­чен 

4) 

Ответ: 19,2 см.

 

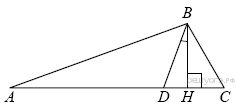№3.      В тре­уголь­ни­ке АВС углы А и С равны 20° и 60° со­от­вет­ствен­но. Най­ди­те угол между вы­со­той ВН и бис­сек­три­сой BD.

 

Решение.

Из тре­уголь­ни­ка АВС най­дем ∠АВС:

 

 

 — биссектриса, следовательно, 

Треугольник НВС — прямоугольный, сле­до­ва­тель­но:

 

 

Найдём угол DBH:

 Ответ: 20°.

№4.     В тре­уголь­ни­ке АВС углы А и С равны 20° и 60° соответственно. Най­ди­те угол между вы­со­той ВН и бис­сек­три­сой BD.

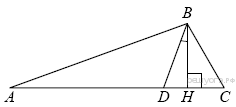Решение.

Найдем 

 

 

 

Так как BD - биссектриса, то 

Треугольник HBC- прямоугольный. Так как  то 

 

Таким образом, ис­ко­мый угол DBH равен 

 

Ответ: 

 

 

Задания типа № 25.

 

№1.  В па­рал­ле­ло­грам­ме KLMN точка B — се­ре­ди­на сто­ро­ны KN. Из­вест­но, что BL = BM. До­ка­жи­те, что дан­ный па­рал­ле­ло­грамм — пря­мо­уголь­ник.

Решение.

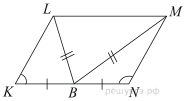
Про­ти­во­по­лож­ные сто­ро­ны па­рал­ле­ло­грам­ма равны, то есть  Рас­смот­рим тре­уголь­ни­ки  и , в них равно   равно  и  равно  сле­до­ва­тель­но тре­уголь­ни­ки равны по трём сторонам, а значит, 

Вспомним также, что про­ти­во­по­лож­ные углы па­рал­ле­ло­грам­ма равны, следовательно:

 

 

Сумма углов па­рал­ле­ло­грам­ма 360°:

 

 

Все углы па­рал­ле­ло­грамм прямые, а следовательно, этот па­рал­ле­ло­грамм — прямоугольник

 

№2.       В па­рал­ле­ло­грам­ме KLMN точка B — се­ре­ди­на сто­ро­ны KN. Из­вест­но, что BL = BM. До­ка­жи­те, что дан­ный па­рал­ле­ло­грамм — пря­мо­уголь­ник.

 

 

Решение.

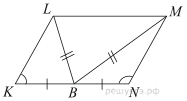
Про­ти­во­по­лож­ные сто­ро­ны па­рал­ле­ло­грам­ма равны, то есть  Рас­смот­рим тре­уголь­ни­ки  и , в них равно   равно  и  равно  сле­до­ва­тель­но тре­уголь­ни­ки равны по трём сторонам, а значит, 

Вспомним также, что про­ти­во­по­лож­ные углы па­рал­ле­ло­грам­ма равны, следовательно:

 

 

Сумма углов па­рал­ле­ло­грам­ма 360°:

 

Все углы па­рал­ле­ло­грамм прямые, а следовательно, этот па­рал­ле­ло­грамм — прямоугольник.

№3.     В па­рал­ле­ло­грам­ме ABCD диа­го­на­ли AC и BD пе­ре­се­ка­ют­ся в точке O. До­ка­жи­те, что пло­щадь па­рал­ле­ло­грам­ма ABCD в че­ты­ре раза боль­ше пло­ща­ди тре­уголь­ни­ка BOC.

Решение.

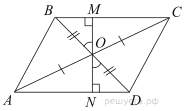
Проведём вы­со­ту  так, чтобы она про­хо­ди­ла через точку Углы  и  равны друг другу как вертикальные. Вспом­ним также, что диа­го­на­ли де­лят­ся точ­кой пе­ре­се­че­ния пополам, следовательно,  Рас­смот­рим тре­уголь­ни­ки  и , они прямоугольные, имеют рав­ные углы и рав­ные гипотенузы, сле­до­ва­тель­но эти тре­уголь­ни­ки равны, а зна­чит равны от­рез­ки  и . Таким образом, 

Площадь па­рал­ле­ло­грамм равна  а пло­щадь тре­уголь­ни­ка 

 

 

№4.       Докажите, что бис­сек­три­сы углов при ос­но­ва­нии рав­но­бед­рен­но­го тре­уголь­ни­ка равны.

Решение.

Имеем: 

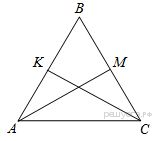
Докажем, что .

1)  по сто­ро­не и двум при­ле­жа­щим к ней углам:

а)  — общая;

б)  по свой­ству углов рав­но­бед­рен­но­го треугольника;

в)  по опре­де­ле­нию бис­сек­три­сы и ра­вен­ству углов при ос­но­ва­нии рав­но­бед­рен­но­го треугольника.

2)  как со­от­вет­ству­ю­щие эле­мен­ты рав­ных треугольников.

 

Задания типа № 26.

№1. В тре­уголь­ни­ке ABC на его ме­ди­а­не BM от­ме­че­на точка K так, что BK : KM = 10 : 9. Прямая AK пе­ре­се­ка­ет сто­ро­ну BC в точке P. Найдите от­но­ше­ние пло­ща­ди четырёхугольника KPCM к пло­ща­ди тре­уголь­ни­ка ABС

Решение.

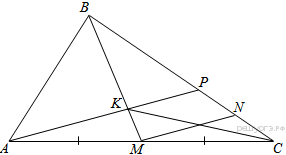
Пусть площадь треугольника  равна 

Проведём прямую  параллельную  Точка  — середина  следовательно,  — средняя линия треугольника значит,  По теореме Фалеса для угла  находим:  а так как  получаем, что 

Стороны треугольников  и  сонаправлены, их площади относятся как произведение отношений сонаправленных сторон, поэтому

 

то есть  откуда , в то время как следовательно, 

Тем самым, для искомого отношения площадей имеем:

 

Ответ: 

 

№2.   Из вер­ши­ны прямого угла C тре­уголь­ни­ка ABC про­ве­де­на высота CP. Ра­ди­ус окружности, впи­сан­ной в тре­уголь­ник BCP, равен 42, тан­генс угла BAC равен  Най­ди­те радиус окружности, впи­сан­ной в тре­уголь­ник ABC.

Решение.

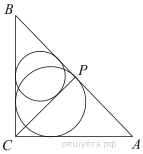
Угол BAC равен углу BCP так как  и . Так как тан­генс это от­но­ше­ние про­ти­во­ле­жа­ще­го ка­те­та к прилежащему, имеем:  Тогда  а ги­по­те­ну­за  по тео­ре­ме Пифагора. Пло­щадь тре­уголь­ни­ка равна про­из­ве­де­нию по­ло­ви­ны его пе­ри­мет­ра на ра­ди­ус впи­сан­ной окружности, но пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния катетов, имеем:

 

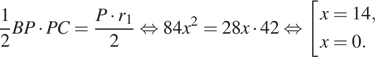
Таким образом, а  Так как  то а  по тео­ре­ме Пифагора.

В тре­уголь­ни­ке  пло­щадь равна про­из­ве­де­нию по­ло­ви­ны его пе­ри­мет­ра на ра­ди­ус впи­сан­ной в него окружности, но пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния катетов, имеем:

 

Ответ: 

 

№3.         Диагонали четырёхугольника , вер­ши­ны ко­то­ро­го рас­по­ло­же­ны на окружности, пе­ре­се­ка­ют­ся в точке . Известно, что  = 74°,  = 102°,  = 112°. Най­ди­те .

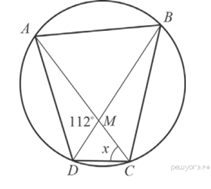Решение.

Пусть .

 = 180° − 112° = 68°;

;

 = 102° − x;

 + 102° − x = 68°; x =  + 34°.

 = 74°;  = x;  = 74° − x; 2x = 108°, x = 54°.

Ответ: 54°.

№4.    Из вер­ши­ны пря­мо­го угла C тре­уголь­ни­ка ABC про­веде­на вы­со­та CP. Ра­ди­ус окружности, впи­сан­ной в тре­уголь­ник BCP, равен 75, тан­генс угла BAC равен  Най­ди­те ра­ди­ус окружности, впи­сан­ной в тре­уголь­ник ABC.

Решение.

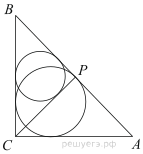
Рассмотрим тре­уголь­ни­ки  и  они прямоугольные. Углы и  равны, как углы с вза­им­но пер­пен­ди­ку­ляр­ны­ми сторонами, следовательно, тре­уголь­ни­ки  и  по­доб­ны по двум углам, их ко­эф­фи­ци­ент по­до­бия  Найдём синус угла 

 

 

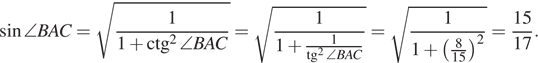
В по­доб­ных тре­уголь­ни­ках со­от­вет­ствен­ные эле­мен­ты пропорциональны, следовательно, 

 

Ответ: 85.