Добавить материал

и получить 10 документов
и свидетельство СМИ

Изображение пользователя Шкода Лидия Ильинична Шкода Лидия Ильинична

Повторение тригонометрии. Вычисление значений тригонометрических выражений.

  • Контроль знаний
  • docx
  • 07.11.2021
Публикация в СМИ для учителей

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал
В работу включены задания по вычислению значений тригонометрических функций по зачению одной из них, задания на формулы сложения, приведения, на формулы двойного угла, на четность, нечетность, периодичность тригонометрических функций. Материал можно использовать при повторении и при подготовке к экзаменам по математике базового и профильного уровня.
Иконка файла материала Тригонометрия. Повторение.docx

 

Повторение тригонометрии.

        Вычисление зна­че­ний тригонометрических выражений

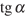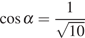
1. Най­ди­те http://reshuege.ru/formula/51/5109f2bba671ceff4332c0b6f3a316b5p.png, если http://reshuege.ru/formula/7e/7e264e38536eb3a2f09eb5707471d4b9p.png

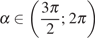и http://reshuege.ru/formula/4e/4e814d27f87c53faa5f17be0df36b4e8p.png.

Ре­ше­ние.

По­сколь­ку угол альфа лежит в четвёртой чет­вер­ти, его тан­генс от­ри­ца­те­лен. По­это­му

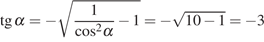http://reshuege.ru/formula/06/067458c6d6037b936a5c048946c7e494p.png.

Ответ: -3.

Ответ: -3

26775

-3

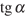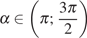
2.  Най­ди­те http://reshuege.ru/formula/51/5109f2bba671ceff4332c0b6f3a316b5p.png, если http://reshuege.ru/formula/23/23af8025142f2684f89d7a6bc3ce8938p.pngи http://reshuege.ru/formula/a8/a89e3efc2e97e87dbfbcc9f9b7b2248fp.png

Ре­ше­ние.

По­сколь­ку 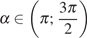http://reshuege.ru/formula/a8/a89e3efc2e97e87dbfbcc9f9b7b2248fp.png, его тан­генс по­ло­жи­те­лен. По­это­му

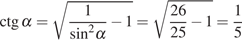http://reshuege.ru/formula/35/35db135f24a5e78b9ba0503d85e749dbp.png.

Тогда

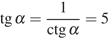http://reshuege.ru/formula/d6/d6118e7aeadc23b469b789a3de48a6f2p.png.

Ответ: 5.

Ответ: 5

26776

5

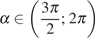3. Най­ди­те http://reshuege.ru/formula/ba/baa683cf98d8c26df65dd7e4be57c7b2p.png, если http://reshuege.ru/formula/e6/e6456157a5d19786c735839f02b527b8p.pngи http://reshuege.ru/formula/4e/4e814d27f87c53faa5f17be0df36b4e8p.png.

Ре­ше­ние.

По­сколь­ку угол http://reshuege.ru/formula/7b/7b7f9dbfea05c83784f8b85149852f08p.pngлежит в чет­вер­той чет­вер­ти, его ко­си­нус по­ло­жи­те­лен. По­это­му

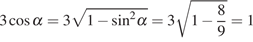http://reshuege.ru/formula/29/297d4718ca32e5bc7433afca64cab0cbp.png.

Ответ: 1.

Ответ: 1

26777

1

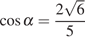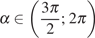4.  Най­ди­те http://reshuege.ru/formula/96/96ef0c5c9a75b2eb28e3ed8b01372a77p.png, если http://reshuege.ru/formula/cc/ccd8059faca3d141ddc1b09a7447059cp.pngи http://reshuege.ru/formula/4e/4e814d27f87c53faa5f17be0df36b4e8p.png.

Ре­ше­ние.

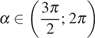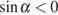По­сколь­ку http://reshuege.ru/formula/4e/4e814d27f87c53faa5f17be0df36b4e8p.png, опре­де­ля­ем, что http://reshuege.ru/formula/cf/cf49717c9215d2e7810d01c7b60d1349p.png. Тогда

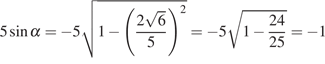http://reshuege.ru/formula/33/33735a919b3b2aac7faa34f043d75eacp.png.

Ответ: -1.

Ответ: -1

26778

-1

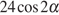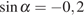5.  Най­ди­те http://reshuege.ru/formula/70/70e430893b3434c36f352225cba7a749p.png, если http://reshuege.ru/formula/9c/9ccbbd5c940a1872ace329182976d12fp.png.

Ре­ше­ние.

Ис­поль­зу­ем фор­му­лу ко­си­ну­са двой­но­го угла 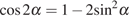http://reshuege.ru/formula/6b/6b7ba23bb7632ab7131653d9d596376ap.png. Имеем:

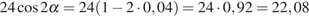http://reshuege.ru/formula/87/87aa980a514dbbd835e53417ade492c9p.png.

Ответ: 22,08.

Ответ: 22,08

26779

22,08

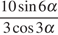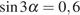6. Най­ди­те http://reshuege.ru/formula/83/832fa81e347f628af33bc77c34e0002bp.png, если http://reshuege.ru/formula/3f/3f7a7afdcaecf74a901e15e900749f49p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

http://reshuege.ru/formula/83/832fa81e347f628af33bc77c34e0002bp.png= http://reshuege.ru/formula/a4/a4adad318aef906ee3e316d4869e8e66p.png.

Ответ: 4.

Ответ: 4

26780

4

7.  Най­ди­те зна­че­ние вы­ра­же­ния 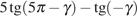http://reshuege.ru/formula/3d/3d8fc586adc6ab06f390e799c05753b4p.png, если http://reshuege.ru/formula/e1/e183d031ac52f7e6495c6dd12a163cfdp.png.

Ре­ше­ние.

В силу пе­ри­о­дич­но­сти тан­ген­са 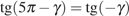http://reshuege.ru/formula/f9/f98a10fb48ca5850669b888224d1f2a6p.png. По­это­му

http://reshuege.ru/formula/20/20aa9e6e3c96d52d00e9801b242aec83p.png.

Ответ: -28.

Ответ: -28

26783

-28

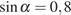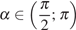8.  Най­ди­те http://reshuege.ru/formula/06/069d80aa0d9f7906d94b6a7af3053ba3p.png, если http://reshuege.ru/formula/6c/6cad753104a229af5f80794967916445p.pngи http://reshuege.ru/formula/ad/ad1522a5e756800f8f1287ca1319137dp.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

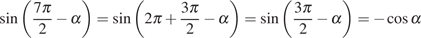http://reshuege.ru/formula/89/89d1ce5a325b42fc6e952ede4dc6d1acp.png.

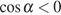По­сколь­ку угол http://reshuege.ru/formula/7b/7b7f9dbfea05c83784f8b85149852f08p.pngлежит в вто­рой чет­вер­ти, http://reshuege.ru/formula/72/72f27bfb9d10dbc0b6c241dd4ff87b3dp.png. Тогда

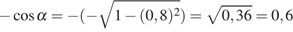http://reshuege.ru/formula/28/28e3455646c29abdab713abdfdb74356p.png.

Ответ: 0,6.

Ответ: 0,6

26784

0,6

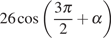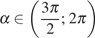9.  Най­ди­те http://reshuege.ru/formula/38/38b952e3a8ece06f71753f3fdabfa8cdp.png, если http://reshuege.ru/formula/e8/e87c49a27bf65cc6a1e9189f7e05f615p.pngи http://reshuege.ru/formula/1f/1f3656507dfe05d5142004b6f3cf844bp.png.

Ре­ше­ние.

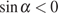По­сколь­ку угол http://reshuege.ru/formula/7b/7b7f9dbfea05c83784f8b85149852f08p.pngлежит в чет­вер­той чет­вер­ти, http://reshuege.ru/formula/cf/cf49717c9215d2e7810d01c7b60d1349p.png. При­ме­ним фор­му­лу при­ве­де­ния, а затем вы­ра­зим синус через ко­си­нус. Имеем:

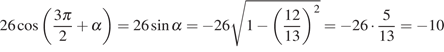http://reshuege.ru/formula/b6/b66a089060a7a1b037a1349bb5db3a5cp.png.

Ответ: −10.

Ответ: -10

26785

-10

10.  Най­ди­те 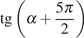http://reshuege.ru/formula/f4/f46f1a21332049623cb446a91f633c7bp.png, если http://reshuege.ru/formula/6c/6ca2f67d92b2b2250af4fdc10042e146p.png

Ре­ше­ние.

Поль­зу­ем­ся пе­ри­о­дич­но­стью тан­ген­са и ис­поль­зу­ем фор­му­лу при­ве­де­ния:

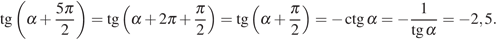
http://reshuege.ru/formula/ca/ca2fd3bb66a39be0c02dd57a35610a11p.png

Ответ: −2,5.

Ответ: -2,5

26786

-2,5

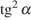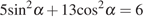11.  Най­ди­те http://reshuege.ru/formula/09/09aa5b22e8afcf26838adf363135e3d0p.png, если http://reshuege.ru/formula/88/88a805efa72cd393b2f30b8abccf8381p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

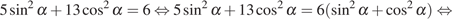
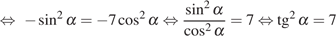http://reshuege.ru/formula/de/de9ea0d954d5826137c2e56cea32a294p.pnghttp://reshuege.ru/formula/ab/ab7d1315bb5894c6a1d8fe09999705dcp.png.

Ответ: 7.

Ответ: 7

26787

7

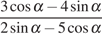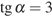12. Най­ди­те http://reshuege.ru/formula/6a/6a6926499a701edb514ae7e27443d502p.png, если http://reshuege.ru/formula/ca/ca07704cedc3b9b4bffc3ad91d75ec3ap.png.

Ре­ше­ние.

Спо­соб 1: http://reshuege.ru/formula/cd/cde6e919aaa657000cb0af61d85d9083p.png. Тогда:

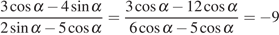http://reshuege.ru/formula/17/17eda458bc9f3285514156d8f1228f55p.png.

Спо­соб 2: раз­де­лим чис­ли­тель и зна­ме­на­тель дроби на 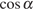http://reshuege.ru/formula/4d/4dc86bcc4da107ee7959075512d77e7ap.png. Тогда:

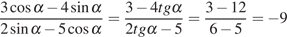http://reshuege.ru/formula/18/18c41cbc36abf54d5d26ce67a1be5879p.png.

Ответ: -9.

Ответ: -9

26788

-9

13.  Най­ди­те http://reshuege.ru/formula/2a/2a96a869db8448dd77ab681dfb566889p.png, если http://reshuege.ru/formula/b9/b9dd412ea60336c83247aa84b01b1d62p.png.

Ре­ше­ние.

Спо­соб 1: http://reshuege.ru/formula/24/24f7ce030cc9bbf95655c41687092ecdp.png. Тогда:

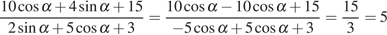http://reshuege.ru/formula/a1/a1123e2f017f6531ba7e274fcffa5e93p.png.

Спо­соб 2: По­де­лим чис­ли­тель и зна­ме­на­тель дроби на 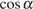http://reshuege.ru/formula/4d/4dc86bcc4da107ee7959075512d77e7ap.png:

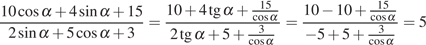http://reshuege.ru/formula/fd/fdd7ec687b721adaef32a15c6fd72f8bp.png.

Ответ: 5.

Ответ: 5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

26789

5

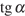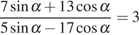14.  Най­ди­те http://reshuege.ru/formula/51/5109f2bba671ceff4332c0b6f3a316b5p.png, если http://reshuege.ru/formula/5a/5a04c2883de553bb24a80c6362616fecp.png.

Ре­ше­ние.

Раз­де­лим чис­ли­тель и зна­ме­на­тель на 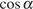http://reshuege.ru/formula/4d/4dc86bcc4da107ee7959075512d77e7ap.png:

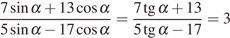http://reshuege.ru/formula/00/00bb52a923cf36a27ae81e520e931c56p.png.

Тогда

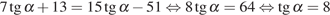http://reshuege.ru/formula/a3/a3ccf6937bbcd9fe5f30e54676091f35p.png.

Ответ: 8.

Ответ: 8

26790

8

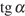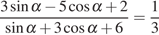15.  Най­ди­те http://reshuege.ru/formula/51/5109f2bba671ceff4332c0b6f3a316b5p.png, если http://reshuege.ru/formula/85/855734eaab36b2de73427bf23dcdba42p.png.

Ре­ше­ние.

Ис­поль­зу­ем свой­ство про­пор­ции:

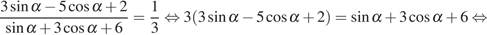
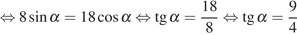http://reshuege.ru/formula/b5/b5ef8266da5029e7d4975198f93ab0d0p.pnghttp://reshuege.ru/formula/90/903fd277bdaa496db30c445c8f1fcf48p.png.

Сле­до­ва­тель­но, http://reshuege.ru/formula/b9/b98ff3a192de09f1d619dce5d96baa20p.png

Ответ: 2,25.

Ответ: 2,25

26791

2,25

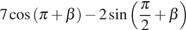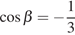16. Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/b0/b071840e72070abaed3964abc34695e1p.png, если http://reshuege.ru/formula/48/486f245165ef1232e3814e48f3417b38p.png.

Ре­ше­ние.

Ис­поль­зу­ем пе­ри­о­дич­ность ко­си­ну­са, не­чет­ность си­ну­са и фор­му­лы при­ве­де­ния:

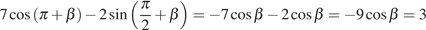http://reshuege.ru/formula/56/56eca8779c9681fc9cf948b9b06776ffp.png.

Ответ: 3.

Ответ: 3

26792

3

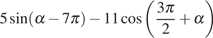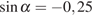17.  Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/3f/3fc2ae70381f736b2dbf4b78fbc4bc7fp.png, если http://reshuege.ru/formula/9c/9c092863347dfd2b81c2444e1ddee88ap.png.

Ре­ше­ние.

В силу не­чет­но­сти и пе­ри­о­дич­но­сти си­ну­са 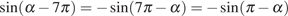http://reshuege.ru/formula/9f/9f847156d866a14bbe81fbc6c14a6cbap.png. Далее по фор­му­лам при­ве­де­ния имеем:

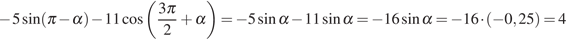http://reshuege.ru/formula/18/18b3e3e2d11caadf8f6048b37b571b5fp.png.

Ответ: 4.

Ответ: 4

26793

4

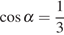18. Най­ди­те http://reshuege.ru/formula/4c/4cf7c2f90f44d3192822170f75accbf0p.png, если http://reshuege.ru/formula/cb/cb146faf78e29636fc052f405ce330f3p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

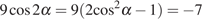http://reshuege.ru/formula/49/49767da03d8c38e3824b62fdfd2d9f42p.png.

Ответ: -7.

Ответ: -7

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Преобразования чис­ло­вых тригонометрических выражений

 

 

1.  Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/77/7764537c13b7649246094875597d2bafp.png.

Ре­ше­ние.

Ис­поль­зу­ем фор­му­лу си­ну­са двой­но­го угла 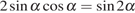http://reshuege.ru/formula/8c/8ca0c761d672107679379a94bbabb037p.png:

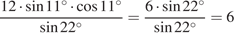http://reshuege.ru/formula/59/596379a421575194df0f7b05d7103a2cp.png.

Ответ: 6.

Ответ: 6

26755

6

2.  Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/6f/6f41b573a2b6fde74e9ba3fecf85b10bp.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

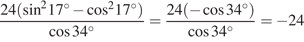http://reshuege.ru/formula/01/01665ebdc218f1d10681efcae7756204p.png.

Ответ: -24.

Ответ: -24

26756

-24

3. Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/52/5245d1e1a403de092af922834d622486p.png.

Ре­ше­ние.

Сход­ствен­ные функ­ции до­пол­ни­тель­ных углов равны, по­это­му

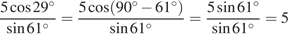http://reshuege.ru/formula/0f/0f27231d2cbf5b26d24dbbb1762bdec2p.png.

Ответ: 5.

Ответ: 5

26757

5

4. Най­ди­те зна­че­ние вы­ра­же­ния 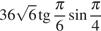http://reshuege.ru/formula/cf/cf0d6ff2e114f4a8f60324aacd7d977cp.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

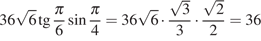http://reshuege.ru/formula/17/170c491877afa4795924e0a6a0fa5cc7p.png.

Ответ: 36.

Ответ: 36

26758

36

5.  Най­ди­те зна­че­ние вы­ра­же­ния 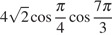http://reshuege.ru/formula/dc/dcf15b78b39efd07fca55050803431acp.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

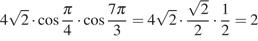http://reshuege.ru/formula/5b/5b4d84032957dd38a8c1f3c82dd39c6cp.png.

Ответ: 2.

Ответ: 2

26759

2

6.  Най­ди­те зна­че­ние вы­ра­же­ния 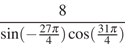http://reshuege.ru/formula/94/949dc631ae3716fb201808f6c85969c2p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

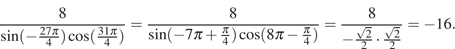
http://reshuege.ru/formula/19/1960a82403729a6a7d3f4ae354f2a77dp.png

Ответ: -16.

Ответ: -16

26760

-16

7.Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/a8/a814240698bd40d927c8ff9d467881a9p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

http://reshuege.ru/formula/b1/b1f770ebfdfd99b5a899647437935af2p.png.

Ответ: -6.

Ответ: -6

26761

-6

8.  Най­ди­те зна­че­ние вы­ра­же­ния 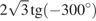http://reshuege.ru/formula/89/891092c598bec3cf47801df461b31f4fp.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

http://reshuege.ru/formula/1e/1ede359764732afbda03793b63e9a0b8p.png.

Ответ: 6.

Ответ: 6

26762

6

9.  Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/52/52adf8832702501e9793074d9d137994p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

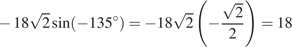http://reshuege.ru/formula/b6/b6b9993340fe2a49b803d6c79b2382e2p.png.

Ответ: 18.

Ответ: 18

26763

18

10.  Най­ди­те зна­че­ние вы­ра­же­ния 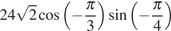http://reshuege.ru/formula/28/28dd3fbb63aaf4df7d558092d45656efp.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

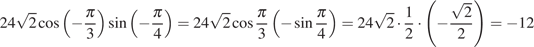http://reshuege.ru/formula/07/07854844f4f533c4558baa3bd717ede1p.png.

Ответ: -12.

Ответ: -12

26764

-12

11.  Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/ed/ed7acdae4179638ff48e867db763b4cdp.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

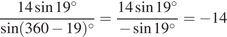http://reshuege.ru/formula/ed/ed7acdae4179638ff48e867db763b4cdp.png= http://reshuege.ru/formula/93/93c17921dd16b2c863859dfeea51d396p.png.

Ответ: -14.

Ответ: -14

 

12. Най­ди­те зна­че­ние вы­ра­же­ния 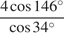http://reshuege.ru/formula/e6/e62ef7729b5dc5eea6b08001f78a083dp.png.

 

Ответ: -4

26766

-4

13. Най­ди­те зна­че­ние вы­ра­же­ния 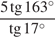http://reshuege.ru/formula/4a/4af9be3de9e674cf824d096b8395ecaap.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

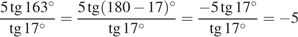http://reshuege.ru/formula/21/21fe897fad43bc572352ea1f34915036p.png.

Ответ: -5.

Ответ: -5

26767

-5

14. Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/f5/f501fad4b6bcc80bd514d2b67d3597e0p.png.

Ре­ше­ние.

Вос­поль­зу­ем­ся пе­ри­о­дич­но­стью си­ну­са:

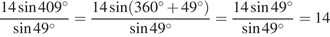http://reshuege.ru/formula/16/16edad0b14f0fcf4870948a39c898419p.png.

Ответ: 14.

Ответ: 14

26769

14

15.  Най­ди­те зна­че­ние вы­ра­же­ния 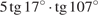http://reshuege.ru/formula/ee/eebb462c5804ce2f14b4a2868e2af318p.png

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

http://reshuege.ru/formula/87/87318b170573b3262001cb57f35821f8p.png.

Ответ: -5.

Ответ: -5

26770

-5

16. Най­ди­те зна­че­ние вы­ра­же­ния 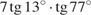http://reshuege.ru/formula/99/9961dcb056f5af667a54ba55ed77ce04p.png.

Ре­ше­ние.

Сход­ствен­ные функ­ции до­пол­ни­тель­ных углов равны. По­это­му

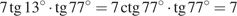http://reshuege.ru/formula/b4/b48eb98e8e25beed6570bf57aa8b6b1cp.png.

Ответ: 7.

Ответ: 7

26771

7

17.  Най­ди­те зна­че­ние вы­ра­же­ния 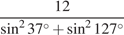http://reshuege.ru/formula/2e/2e29b3fdb8b17efdfa687b6bcaa4d215p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

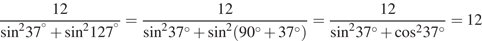http://reshuege.ru/formula/af/af80081fe62715362515f1968899111dp.png.

Ответ: 12.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: 12

26772

12

18.  Най­ди­те зна­че­ние вы­ра­же­ния 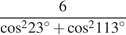http://reshuege.ru/formula/ef/eff0b01c6ba92a913c227d5378583231p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

http://reshuege.ru/formula/2c/2c6f310dcda8da8e74de47aec82728ecp.png.

Ответ: 6.

Ответ: 6

26773

6

19. Най­ди­те зна­че­ние вы­ра­же­ния 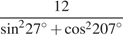http://reshuege.ru/formula/15/1588e3bfc4b242e2a066e69a3eef4698p.png.

Ре­ше­ние.

По­сколь­ку 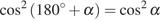http://reshuege.ru/formula/1e/1ed4139adff10106cc71ac807cd19ad6p.pngимеем:

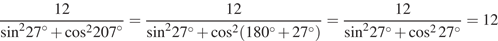http://reshuege.ru/formula/43/43cf457778677dc8ba13ef12f00f6b21p.png.

Ответ: 12.

Ответ: 12

26774

12

20.  Най­ди­те зна­че­ние вы­ра­же­ния 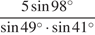http://reshuege.ru/formula/65/6522eba3a4c31df58e8ec53801f1aa63p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

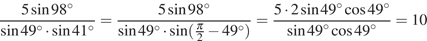
http://reshuege.ru/formula/dd/dd9ad1894471b220b2e20840e308e410p.png

Ответ: 10.

Ответ: 10

77412

10

21.  Най­ди­те зна­че­ние вы­ра­же­ния 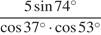http://reshuege.ru/formula/15/15f4c455f9cfc4bd0b40d05c2e46ff21p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

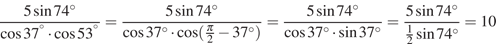http://reshuege.ru/formula/59/596541474f9e7ac95842b651bb318b27p.png.

Ответ: 10.

Ответ: 10

77413

10

22.  Най­ди­те зна­че­ние вы­ра­же­ния: 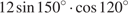http://reshuege.ru/formula/69/6949068e43a00b7a2d7e5ed882bccaaep.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

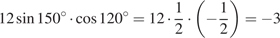http://reshuege.ru/formula/ee/eef4e8ae7ac0fa9356eeb976792abb1dp.png.

Ответ: -3.

Ответ: -3

77414

-3

23.  Най­ди­те зна­че­ние вы­ра­же­ния 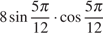http://reshuege.ru/formula/62/62b2a5cbc530c72965cd057d3be52a58p.png.

Ре­ше­ние.

Ис­поль­зу­ем фор­му­лу си­ну­са двой­но­го угла 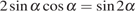http://reshuege.ru/formula/c4/c44edb90ab7aac4c1bedcd0b569d7372p.png:

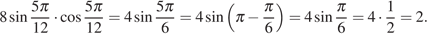
http://reshuege.ru/formula/1c/1c6111d8ddee84feaa992c23c72b70b8p.png

Ответ: 2.

Ответ: 2

245169

2

24.  Най­ди­те зна­че­ние вы­ра­же­ния 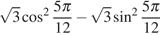http://reshuege.ru/formula/a3/a34b43ac7a18a4d2ca67050973fe33a3p.png.

Ре­ше­ние.

Ис­поль­зу­ем фор­му­лу ко­си­ну­са двой­но­го угла 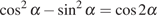http://reshuege.ru/formula/61/61cc8891c27122a7ea5affe8724aa951p.png:

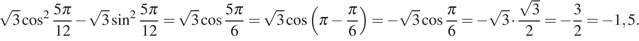
http://reshuege.ru/formula/97/975c3cb2bc04a787d84b40903d619ae8p.png

Ответ: -1,5.

Ответ: -1,5

245170

-1,5

25.  Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/02/02b503a9aa78e8bff8ce53896e769cf7p.png.

Ре­ше­ние.

Ис­поль­зу­ем фор­му­лу ко­си­ну­са двой­но­го угла 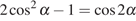http://reshuege.ru/formula/2f/2f4d8b728c2b2558015165dd04d2c032p.png:

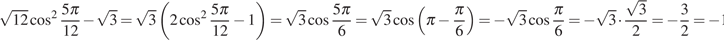
http://reshuege.ru/formula/c3/c3d09130e069ed38f920b3de4e9eef83p.png

Ответ: -1,5.

Ответ: -1,5

 

26. Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/fa/fab9c7ce4e38b257d0ee03a8c8789fffp.png.

Ре­ше­ние.

Ис­поль­зу­ем фор­му­лу ко­си­ну­са двой­но­го угла 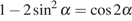http://reshuege.ru/formula/41/41303a7fab95ab14f3d97de2fd4148e3p.png:

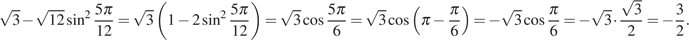
http://reshuege.ru/formula/f5/f5ecae6acbcc1cc6cbb3f56064146edcp.png

Ответ: −1,5.

Ответ: -1,5

245172

-1,5

27.  Най­ди­те http://reshuege.ru/formula/8c/8c8f4f1ade4856a8baa9d1d1d0449022p.png, если http://reshuege.ru/formula/79/79ace79dc0791fde4d866f794a283a80p.png.

Ре­ше­ние.

По фор­му­ле 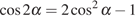http://reshuege.ru/formula/7b/7ba19d32abd5ef48c26c680f95a4127ep.pngимеем:

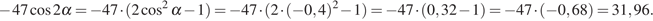
http://reshuege.ru/formula/f8/f81ce2cf56237c283b4286e3d24d0881p.png

Ответ:31,96.

Ответ: 31,96

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

26765

-14

245169

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Применение формул приведения и преобразование выражений.

 

1.  Най­ди­те зна­че­ние вы­ра­же­ния 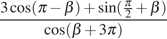http://reshuege.ru/formula/70/70571b0f98aa0355fd7b8780ef669957p.png.

Ре­ше­ние.

В силу пе­ри­о­дич­но­сти ко­си­ну­са 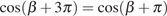http://reshuege.ru/formula/c1/c1608d2e5d0126ca847ecd057756d819p.png. Далее ис­поль­зу­ем фор­му­лы при­ве­де­ния:

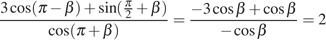http://reshuege.ru/formula/4c/4c86ba6817c14b037b0027e24af8fc5ep.png.

Ответ: 2.

Ответ: 2

26781

2

2.  Най­ди­те зна­че­ние вы­ра­же­ния 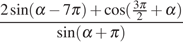http://reshuege.ru/formula/45/45ae4ae9bbe5553fe7e0081b69b86338p.png.

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

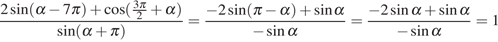http://reshuege.ru/formula/ab/ab50669fba962b2fb40e704421f60a02p.png.

Ответ: 1.

Ответ: 1

26782

1

3.

Най­ди­те зна­че­ние вы­ра­же­ния 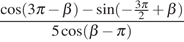http://reshuege.ru/formula/62/62308d3186ba0f1af895f91984df0be7p.png.

Ре­ше­ние.

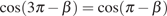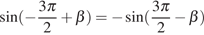В силу пе­ри­о­дич­но­сти ко­си­ну­са и сим­мет­рич­но­сти си­ну­са http://reshuege.ru/formula/d6/d660bf5f10e0c3fa2d24b2c11c8485c8p.png, http://reshuege.ru/formula/ec/ece4182745f3b2e41af73946f4829765p.png. Далее ис­поль­зу­ем фор­му­лы при­ве­де­ния:

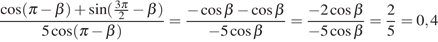http://reshuege.ru/formula/d7/d723ae6ef29cb2cead1bbde1e9ebdc34p.png.

Ответ: 0,4.

Ответ: 0,4

64623

0,4

4.

Най­ди­те зна­че­ние вы­ра­же­ния 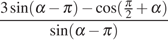http://reshuege.ru/formula/76/76bbab195e66898b8a24dc7d56f65695p.png.

Ре­ше­ние.

В силу не­чет­но­сти си­ну­са http://reshuege.ru/formula/ff/fff4ba464b91b32ac92715d623de71eep.png. Далее ис­поль­зу­ем фор­му­лы при­ве­де­ния:

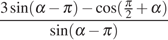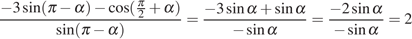http://reshuege.ru/formula/76/76bbab195e66898b8a24dc7d56f65695p.png= http://reshuege.ru/formula/9a/9a7b16013e3b72db4a4aa8dbb88a931dp.png.

Ответ: 2.

Ответ: 2

64693

2

5.

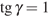Най­ди­те зна­че­ние вы­ра­же­ния http://reshuege.ru/formula/8f/8f2cb6a26b26f688cc49dfef7175fe97p.png, если http://reshuege.ru/formula/9f/9f149fed58f3145b44f581ac3043ac03p.png.

Ре­ше­ние.

В силу пе­ри­о­дич­но­сти тан­ген­са 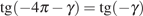http://reshuege.ru/formula/66/660b8ec8660d5ae4445ff64e0471ac51p.png. По­это­му

http://reshuege.ru/formula/42/4213b9aff5a9b3235098fd4d8c538debp.png.

Ответ: −7.

Ответ: -7

64767

-7

6.

Най­ди­те http://reshuege.ru/formula/fd/fd41340d79a3aea1184820223de2173cp.png, если http://reshuege.ru/formula/85/85408406f6f5c68ec4a70bfc9d84f6cfp.png.

Ре­ше­ние.

Най­ди­те http://reshuege.ru/formula/4d/4d3669e9855845ef1f2c90f4d8a4772ep.png, если http://reshuege.ru/formula/85/85408406f6f5c68ec4a70bfc9d84f6cfp.png.

По­де­лим чис­ли­тель и зна­ме­на­тель дроби на 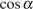http://reshuege.ru/formula/4d/4dc86bcc4da107ee7959075512d77e7ap.png:

http://reshuege.ru/formula/4d/4d3669e9855845ef1f2c90f4d8a4772ep.png= http://reshuege.ru/formula/a0/a08f9636d0d32feb0f22c3d49f8ed4e0p.png.

Ответ: 4.

Ответ: 4

 

7. Вычислить выражение

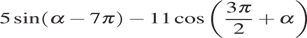http://reshuege.ru/formula/3f/3fc2ae70381f736b2dbf4b78fbc4bc7fp.png, если sin α = 0,4.

Ответ: -6,4.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

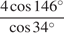http://reshuege.ru/formula/e6/e62ef7729b5dc5eea6b08001f78a083dp.png= http://reshuege.ru/formula/a7/a73e321e4fe7066cc9b5e568d3b260b8p.png.

Ответ: -4.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

26781

2

Повторение тригонометрии. Най­ди­те , если . Ре­ше­ние Преобразования чис­ло­вых тригонометрических выражений 1 Ответ: 12 26772 12 18. Применение формул приведения и преобразование выражений

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также