ПР 2. ДИСКОНТУВАННЯ. ПОТОКИ ПЛАТЕЖІВ. РЕНТИ

 ПР 2. Дисконтування. Потоки платежів. Ренти

2.1 Мета роботи

Метою заняття є вивчення математичної бази для розрахунку потоків платежів, ренти, на основі дисконтування..

2.2                 Методичні вказівки з організації самостійної роботи студентів

Дисконтована вартість. У фінансових розрахунках виникає необхідність порівнювати між собою різні суми грошей в різні моменти часу.

Щоб порівняти суми грошей в часі, їх необхідно привести до одного часового знаменника. В практиці фінансових розрахунків прийнято приводити суми коштів, які одержить інвестор, до сьогоднішнього дня (початкової точки відліку), тобто визначити величину суми Р, яка в майбутньому повинна скласти задану величину Pn. В цьому випадку Р буде називатись поточною (теперішньою) величиною суми Pn.

Теперішня вартість – грошова вартість майбутніх доходів на теперішній час. Розрахунки теперішньої вартості здійснюють за допомогою дисконтування.

Дисконтування – це зведення економічних показників різних років до порівнянного в часі вигляду. Дисконтування здійснюється за допомогою коефіцієнта дисконтування (дисконтуючого множника), в основі якого лежить формула складних відсотків і значення якого також табульовані (див. Додаток 2).

Цю задачу вирішують за допомогою формули (4.24), яка називається формулою дисконтованої або приведеної вартості. Вона випливає з формули (4.10):

.                                                                 (2.1)

де Pn – це майбутня вартість;

Р – дисконтована або приведена вартість (в літературі в якості синонімів використовують також терміни сьогоднішня, дійсна, поточна вартість);

 – це коефіцієнт дисконтування. Економічний зміст аамес коефіцієнта полягає в тому, що його величина відповідає поточній вартості однієї грошової одиниці, яка буде одержана в кінці періоду n при складному відсотку r. Його величина залежить від тривалості часового періоду і необхідної ставки дисконту.

 При нарахуванні складного відсотку m разів на рік формула (2.1) набуває вигляду:

,                                                       (2.2)

На підставі формул (2.1), (2.2)) одержуємо відповідно формули дисконтованої вартості для простого відсотку:

.                                                            (2.3)

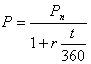.                                                              (2.4)

Визначення періоду нарахування відсотків. На практиці виникають питання визначення періоду часу, який необхідний для збільшення суми Р до значення Рn при нарахуванні відсотку r.

Для простого відсотку з формули (2.3) одержимо:

                                                                 (2.5)

Приклад

За який строк вклад в 8000 грн. збільшиться в 3 рази при ставці 20 % річних?

Приклад

За який строк вклад в 5000 грн. зросте до 13500 грн. при ставці 25 % річних?

Нехай рік дорівнює 365 дням, тоді 0,8 року еквівалентно . Таким чином, вклад буде дорівнювати 13500 грн. через 6 років і 292 дні.

Потоки платежів, ренти

1                   Потік платежів – це послідовність величин самих платежів і моментів часу, коли вони здійснені. Величиною потоку в момент Т називається сума платежів потоку, дисконтованих до цього моменту

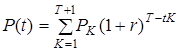.                                     (2.6)

Якщо знайти величину потоку в момент Т, тоді в будь-який інший момент  величина потоку . Величина  називається сучасною (поточною) величиною потоку. Якщо є останній платіж, то величина  потоку в момент цього платежу називається скінченою величиною потоку.

2                   Потік платежів  С  з постійними проміжками між ними називається рентою.

 Кінцева річна рента

Це найпростіша рента: в ній тільки один платіж С в рік, тривалість її  років, річна процентна ставка . На рентні платежі нараховуються складні відсотки. Сучасна величина ренти  дорівнює

,                                             (2.7)

  де С – розмір платежу.

«Вічна» річна рента

Під «вічною» річною рентою розуміється рента, послідовність платежів якої необмежена, передбачається, що рента  виплачуватиметься необмежено довго. Нарощена величина цієї ренти нескінченна, але сучасна величина дорівнює .

2.3 Приклади аудиторних задач

1. За прогнозами фахівців для ремонту обладнання, який доведеться здійснити через 10 років, будуть потрібні $25000. В банк під 10% річних фірмою було вкладено $10000.
Чи вистачить суми, що буде на рахунку фірми через 10 років, для відповідного ремонту?
Через скільки років на банківському рахунку фірми буде необхідна сума?

2. Для вашого проекту ви взяли кредит $56000 під 100% річних. Схема повернення основної суми боргу та відсотків за кредит така: повертати щорічно, в кінці кожного року, рівними сумами (починаючи з першого року).
Якою повинна бути сума щорічного повернення, щоб повернути весь борг через 8 років?

3. Пенсійний фонд пропонує свої послуги за таких умов: через 10 років протягом наступних 20-ти років забезпечується пенсія розміром $5000 щорічно, якщо зараз внести на рахунок фонду необхідну грошову суму під 12% річних.

Яку суму необхідно внести на початковому етапі?

4. Завод збирається придбати нове обладнання. Фахівці розрахували, що протягом п’яти років щорічно прибутки від його експлуатації будуть становити: з першого по третій роки — по 50000 гривень, а в четвертий та  п’ятий роки — 60000 гривень.
Виходячи з наявної інформації, розрахуйте сумарну теперішню вартість прибутків заводу від експлуатації обладнання, якщо ставка дисконту становить 10%.

5. Ви вибираєте нове місце роботи. Вам запропонована однакова річна сума зарплати (12000 грош. од.), але з різними графіками виплати:
варіант А — аванс у січні (6000 грош. од.), виплата «під розрахунок» у грудні (6000 грош.од.);
варіант Б — щомісячна виплата протягом усього року (по 1000 грош. од.).
а)Який варіант ви оберете і чому (ставка відсотка становить 10%)?
б)У якому місяці обидва варіанти дадуть однаковий результат (R = 10%)?
в)Яким буде ваш вибір варіанта, якщо ставка відсотка становить 25%?
г)Яким буде ваш вибір варіанта, якщо R = 0% ?