Вариант 1

                                                                                  запишите                                         задачи

Площадь четырѐхугольника можно вычислить по формуле S =  d₁ d₂ sin , где d₁ и d₂ – длины диагоналей четырѐхугольника,  – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d₂, если d₁=14, sin  = 1/12, a S = 8,75.

2.   Найдите значения кусочно-непрерывной функции.

f(x)=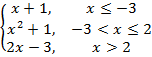

3.   Разработать и записать алгоритм решения задачи. Найти сумму натуральных чисел от a до b (b>a).

Вариант 2

Составьте блок-схему и запишите алгоритм решения задачи на алгоритмическом языке.

1.   Найдите значение переменной, заданной формулой:

Закон Менделеева-Клапейрона можно записать в виде PV = vRT, где P – давление (в паскалях), V – объѐм (в м³), ν – количество вещества (в молях), T – температура (в градусах Кельвина), а R – универсальная газовая постоянная, равная 8,31 Дж/(К  моль). Пользуясь этой формулой, найдите объѐм V (в м³), если T = 250 К, P = 23 891,25 Па, ν = 48,3 моль.

2.   Найдите значения кусочно-непрерывной функции.

f(x)=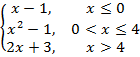

3.   Разработать и записать алгоритм решения задачи. Найти произведение целых чисел от a до b.

Вариант 3

                                                                                  запишите                                         задачи

Закон Кулона можно записать в виде F = k , где F – сила взаимодействия зарядов (в ньютонах), q₁ и q₂ – величины зарядов (в кулонах), k – коэффициент пропорциональности (в Н·м²/Кл²), а r – расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда q₁ (в кулонах), если k = 910⁹ Н·м²/Кл², q₂ = 0,006 Кл, r = 300 м, а F = 5,4 Н.

2.   Найдите значения кусочно-непрерывной функции.

f(x)=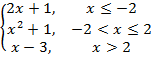

3.   Разработать и записать алгоритм решения задачи.

Найти число перестановок из n элементов, если Р_n=n!=1·2·3·…·n.

Вариант 4

Составьте блок-схему и запишите алгоритм решения задачи на алгоритмическом языке.

1.   Найдите значение переменной, заданной формулой:

Закон всемирного тяготения можно записать в виде F =  , где F – сила притяжения между телами (в ньютонах), m₁ и m₂ – массы тел (в килограммах), r – расстояние между центрами масс (в метрах), а γ – гравитационная постоянная, равная 6,67·10^-11 H·м²/кг² . Пользуясь формулой, найдите массу тела m₁ (в килограммах), если F = 83,375 Н, m₂ = 410⁹ кг, а r = 4 м.

2.   Найдите значения кусочно-непрерывной функции.

f(x)=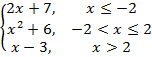

3.   Разработать и записать алгоритм решения задачи.

Найти сумму k первых членов последовательности, заданной формулой n-го

члена a_n=

Вариант 5

                                                                                  запишите                                         задачи

Площадь параллелограмма S (в м²) можно вычислить по формуле S = absin ,где a ,b — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и sin  =

0,5.

2.   Найдите значения кусочно-непрерывной функции.

f(x)=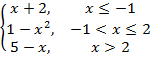

3.   Разработать и записать алгоритм решения задачи.

Найдите k первых членов арифметической прогрессии, в которой a₁=5, d=3.

Вариант 6

Составьте блок-схему и запишите алгоритм решения задачи на алгоритмическом языке.

1.   Найдите значение переменной, заданной формулой:

Радиус описанной около треугольника окружности можно найти по формуле R = , где a — сторона треугольника,  — противолежащий этой стороне угол. Пользуясь этой формулой, найдите sin , если a = 0,6, а R = 0,75.

2.   Найдите значения кусочно-непрерывной функции.

f(x)=

3.   Разработать и записать алгоритм решения задачи.

Найдите k первых членов геометрической прогрессии, в которой b₁=5, q=3.