
Министерство образования и науки Краснодарского края
Государственное бюджетное профессиональное образовательное учреждение
Краснодарского края
«Армавирский механико – технологический техникум»
Методическое пособие
для проведения
практического занятия
на тему:
«ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ, ИСПОЛЬЗУЕМЫЕ ПРИ ВЫЧЕРЧИВАНИИ КОНТУРОВ ТЕХНИЧЕСКИХ ДЕТАЛЕЙ»
по дисциплине: «Инженерная графика»
для студентов 2 курса
спец. 15.02.01, 15.02.05, 19.02.03, 19.02.06, 19.02.08, 19.02.09
очного и заочного отделения
Разработал преподаватель: Е.В. Игнатова
2016
1 ЦЕЛЬ РАБОТЫ:
1.1 Получить сведения о делении окружности на равные части, различных видах сопряжения.
1.2 Выполнить изображение детали и нанести размеры.
2 ОБЩИЕ СВЕДЕНИЯ
2.1 Деление окружности на равные части
Деление окружности на три равные части (рис.1 а).
Деление окружности на три равные части выполняем с помощью циркуля. Из лежащей на окружности точки А как из центра проводим дугу. Радиус R дуги равен радиусу заданной окружности. Дуга пересекает окружность в точках 2 и 3. Точки 1, 2, 3 делят окружность на три равные части.
Деление окружности на шесть равных частей (рис. 1б).
Из центров в точках 1 и 4 раствором циркуля, равным радиусу заданной окружности R, проводим дуги. Точки 1, 2, 3, …, 6 делят окружность на шесть равных частей.
Деление окружности на двенадцать равных частей (рис. 1в).
Из центров в точках 1, 4, 7, 10 раствором циркуля, равным радиусу заданной окружности R, проводим дуги. Точки 1, 2, 3,…, 12 делят заданную окружность на двенадцать равных частей.
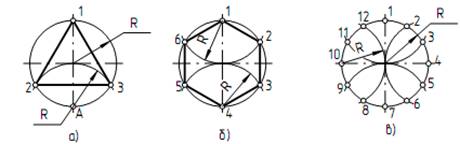
Рисунок 1
Деление окружности на четыре и восемь равных частей (рис. 2а).
Взаимно перпендикулярные центровые линии АС и BD делят окружность на четыре равные части. Для того чтобы разделить окружность на восемь равных частей, проводим биссектрисы углов АОВ и ВОС. Точки 1, 2, 3,…, 8 делят окружность на восемь равных частей.
Деление окружности на пять равных частей (рис. 2б).
Из центра А раствором циркуля, равным радиусу заданной окружности R, проводим дугу, которая пересекает окружность в точках В и С. Отрезок ВС делит радиус окружности ОА на две равные части в точке D. Из центра D проводим дугу 1K радиусом R1 (R1 = 1D). Отрезок 1K есть сторона правильного пятиугольника. От точки 1 по заданной окружности откладываем хорды, которые равны отрезку 1K.
Деление окружности на семь равных частей (рис. 2в).
Из центра А раствором циркуля, равным радиусу заданной окружности R, проводим дугу, которая пересекает окружность в точках В и С. Отрезок ВС делит радиус окружности ОА на две равные части в точке D. От точки 1 по заданной окружности откладываем хорды, которые равны отрезку ВD, где BD – сторона правильного семиугольника.

Рисунок 2
2.2 Сопряжения
При выполнении геометрических построений часто приходится плавно соединять прямые и кривые линии. Плавный переход одной линии в другую называется сопряжением.
 Для
построения сопряжения необходимо знать величину радиуса сопряжения, найти
центры и точки сопряжений. Элементы сопряжений показаны на рис.
Для
построения сопряжения необходимо знать величину радиуса сопряжения, найти
центры и точки сопряжений. Элементы сопряжений показаны на рис.
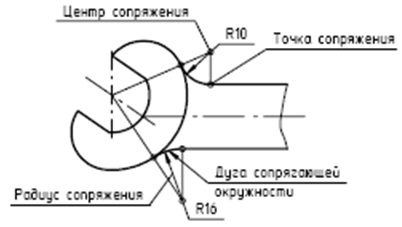
Дуга окружности, по которой одна линия плавно переходит в другую, называется дугой сопрягающей окружности.
Радиус этой окружности – радиус сопряжения. Центр этой
Рисунок 3 окружности – центр сопряжения. Точка, в которой одна линия плавно переходит в другую, – точка сопряжения. Построение сопряжений рассмотрим на примере универсального «чертежа-справочника» (рис. 4), при вычерчивании которого применены все основные виды сопряжений.
Использованные при построении чертежа виды сопряжений отмечены на нем пронумерованными стрелками, а на рис. показано подробное построение каждого из обозначенных сопряжений с последующим кратким описанием.
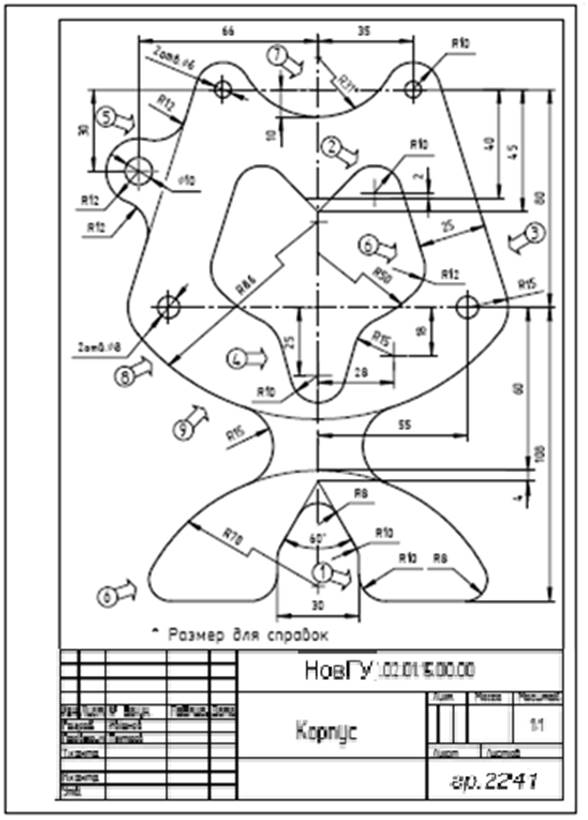
Рисунок 4
Сопряжение сторон острого и тупого углов дугой окружности заданного радиуса R1 (рис. 5а, б).
Расстояние от центра сопряжения до каждой стороны угла равно заданному радиусу сопряжения R1. Чтобы найти центр сопряжения, необходимо провести две вспомогательные прямые, параллельные каждой стороне угла, на расстоянии R1 от них. Для проведения вспомогательных прямых из произвольных точек, лежащих на сторонах угла, раствором циркуля, равным R1, выполняем две-три засечки и к ним проводим касательные.
Точка пересечения О построенных касательных и будет центром сопряжения. Точки сопряжения получим, опустив из точки О перпендикуляры к каждой стороне заданного угла.
Сопряжение сторон прямого угла дугой окружности заданного радиуса R1 (рис. 5в).
Из вершины прямого угла как из центра проводим дугу радиуса R1. Из точек пересечения построенной дуги со сторонами заданного угла как из центров выполняем две засечки радиусом R1. На пересечении засечек определяем точку О – центр сопряжения. Из него проводим дугу сопрягающей окружности.

Рисунок 5
Построение касательной к окружности (рис. 6а). Дана окружность радиуса R1 с центром в точке О1 и точка А, не принадлежащая окружности. Требуется через точку А провести касательную к заданной окружности. Соединяем точку А с центром заданной окружности О1. Отрезок О1А делим на две равные части – получаем точку В. Из центра В проводим дугу окружности. Её радиус R = АВ. На пересечении построенной дуги с заданной окружностью находим точку касания N. Через неё и точку А проводим касательную.
Построение касательной к двум окружностям (внешнее касание) (рис.6б).
Даны две окружности с центрами в точках О1 и О2. Их радиусы R1 и R2. Требуется провести к ним внешнюю касательную. Из центра О2 проводим вспомогательную окружность радиуса (R2 – R1). Соединяем центры О1 и О2. Отрезок О1О2 делим на две равные части – получаем точку В. Из центра В проводим дугу окружности. Её радиус R = О2В. На пересечении дуги с вспомогательной окружностью получаем точку N. Через центр О2 и точку N проводим прямую. Её пересечение с окружностью радиуса R2 даст нам первую точку касания М. Через центр О1 проводим отрезок О1K параллельно О2М. Точка K – вторая точка касания. Соединяем точки K и М. Прямая МK есть внешняя касательная к заданным окружностям.
Построение касательной к двум окружностям (внутреннее касание) (рис. 6в).
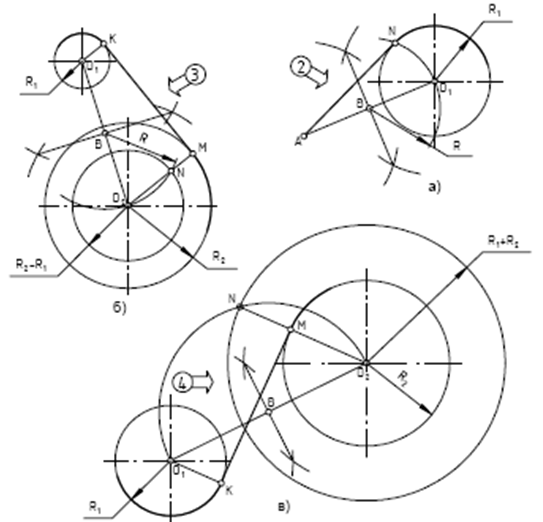
Рисунок 6
Даны две окружности с центрами в точках О1 и О2. Их радиусы R1 и R2. Требуется провести к ним внутреннюю касательную. Из центра О2 проводим вспомогательную окружность радиуса (R2 + R1). Соединяем центры О1 и О2. Отрезок О1О2 делим на две равные части – получаем точку В. Из центра В проводим дугу окружности. Её радиус R = О2В. На пересечении дуги с вспомогательной окружностью получаем точку N. Через центр О2 и точку N проводим прямую, её пересечение с окружностью радиуса R2 даст нам первую точку касания М. Через центр О1 проводим отрезок О1K параллельно О2М. Точка K – вторая точка касания. Соединяем точки K и М. Прямая МK есть внутренняя касательная к заданным окружностям.
Построение внешнего сопряжения дуги и прямой дугой радиуса R (рис. 7а).
Даны дуга окружности радиуса R1 с центром в точке О1 и прямая а. Из центра О1 проводим вспомогательную дугу радиуса (R + R1). Проводим вспомогательную прямую, параллельную заданной прямой, а, на расстоянии радиуса сопряжения R. На пересечении вспомогательных дуги и прямой получаем точку О – центр сопряжения. Проводим прямую ОО1 – получаем первую точку сопряжения. Опускаем перпендикуляр из точки О на прямую а – получаем вторую точку сопряжения. Проводим сопрягающую дугу радиуса R от первой до второй точки сопряжения.
Построение внутреннего сопряжения дуги и прямой дугой радиуса R (рис.7б).
Даны дуга окружности радиуса R1 с центром в точке О1 и прямая а. Из центра О1 проводим вспомогательную дугу радиуса (R1 – R). Проводим вспомогательную прямую, параллельную заданной прямой, а, на расстоянии радиуса сопряжения R. На пересечении вспомогательных дуги и прямой получаем точку О – центр сопряжения. На продолжении прямой ОО1 получаем первую точку сопряжения. Опускаем перпендикуляр из точки О на прямую а. Получаем вторую точку сопряжения. Проводим сопрягающую дугу радиуса R от первой до второй точки сопряжения.
Построение сопряжения двух дуг окружностей дугой, проходящей через заданную точку (внешнее касание) (рис.7 в).
Даны две симметрично расположенные окружности радиуса R1 с центрами в точках О1 и точка А, через которую должна пройти неизвестная дуга сопряжения Rx. Из точки А как из центра проводим дугу радиуса R1. На пересечении дуги с осью симметрии получаем точку В. Соединяем прямой точки В и О1. Из точек В и О1 как из центров проводим дуги произвольного радиуса, но большего, чем половина отрезка ВО1, – получаем точки С и D. Через точки С и D проводим прямую. На пересечении прямой СD c осью симметрии находим центр сопряжения Оx. Соединяем точку Оx с точками О1. Пересечение отрезков ОxO1 c заданными дугами окружностей даст нам точки сопряжения 1 и 2. Проводим дугу радиуса Rx из центра Оx от точки 1 к точке 2.
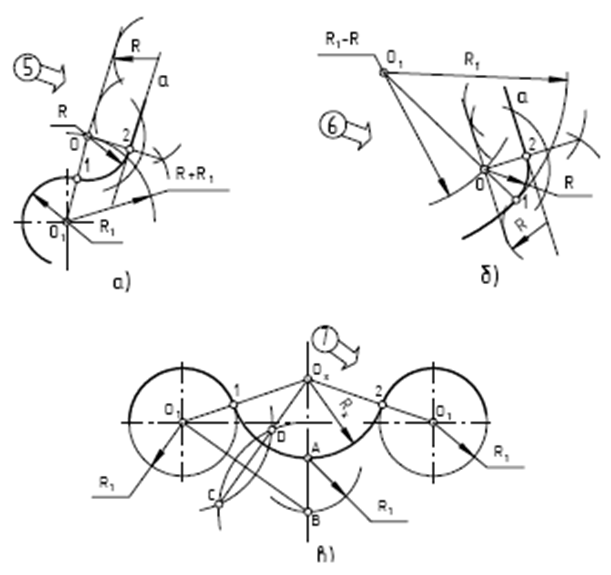
Рисунок 7
Построение внутреннего сопряжения дуг двух окружностей дугой радиуса R (рис.8 а).
Даны две окружности с центрами в точках О1 и О2. Их радиусы R1 и R2. Требуется провести к ним сопрягающую дугу радиуса R c внутренним касанием. Проводим вспомогательную дугу радиуса (R – R1) из центра О1 и дугу радиуса (R – R2) из центра О2. Получаем точку О – центр сопряжения. Проводим прямую ОО1 – получаем точку сопряжения 1. Проводим прямую ОО2 – получаем точку сопряжения 2. Проводим сопрягающую дугу радиуса R из центра О от точки 1 до точки 2.
Построение смешанного сопряжения дуг двух окружностей дугой радиуса R (рис. 8б).
Даны две окружности с центрами в точках О1 и О2. Их радиусы R1 и R2. Требуется провести к ним сопрягающую дугу радиуса R cо смешанным касанием. Проводим вспомогательную дугу радиуса (R – R1) из центра О1 и дугу радиуса (R + R2) из центра О2 – получаем точку О (центр сопряжения). Проводим прямую ОО1 – получаем точку сопряжения 1. Проводим прямую ОО2 – получаем точку сопряжения 2. Проводим сопрягающую дугу радиуса R из центра О от точки 1 до точки 2.
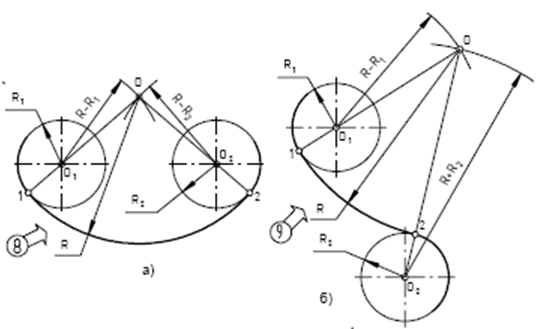
Рисунок 8
ЗАДАНИЕ
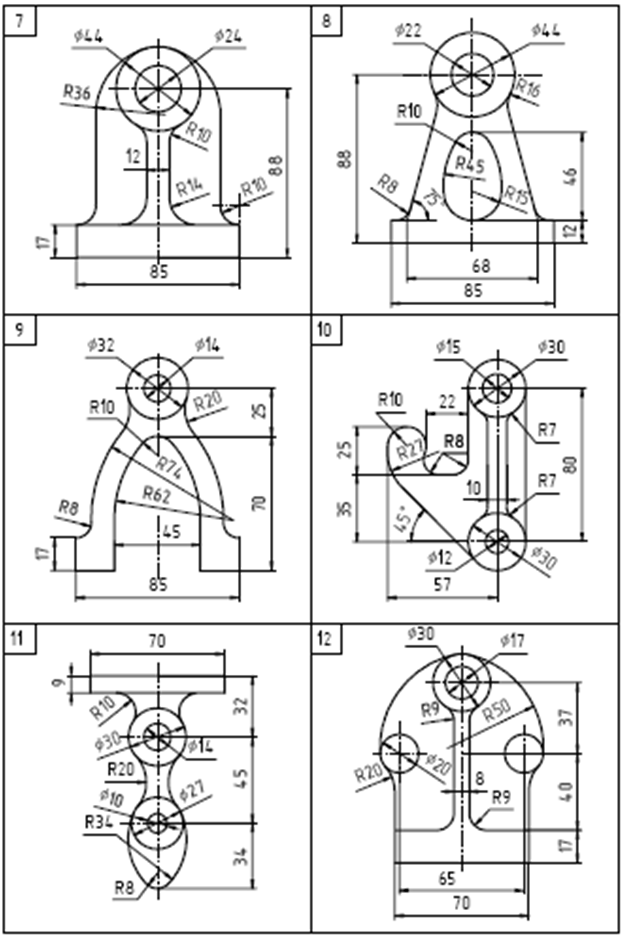
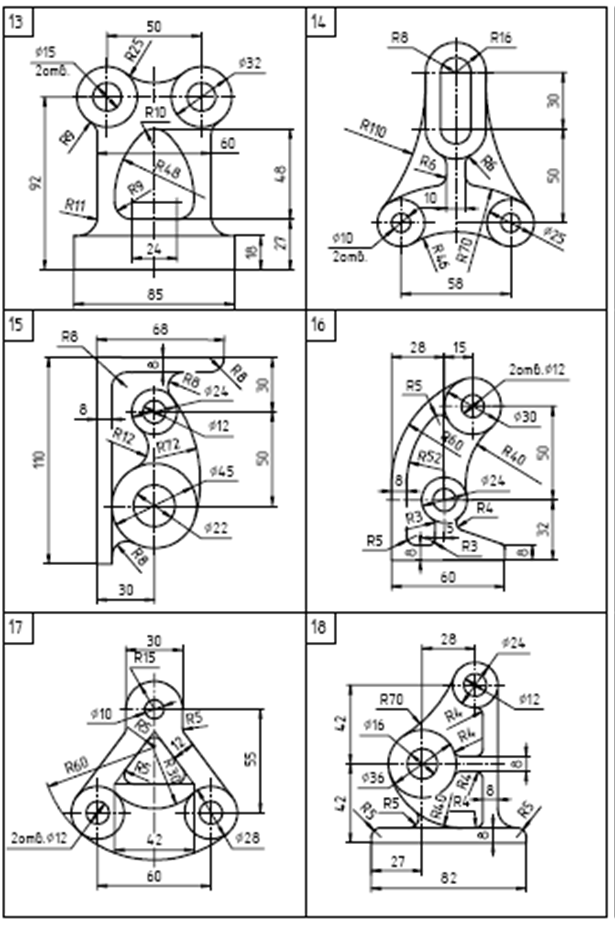
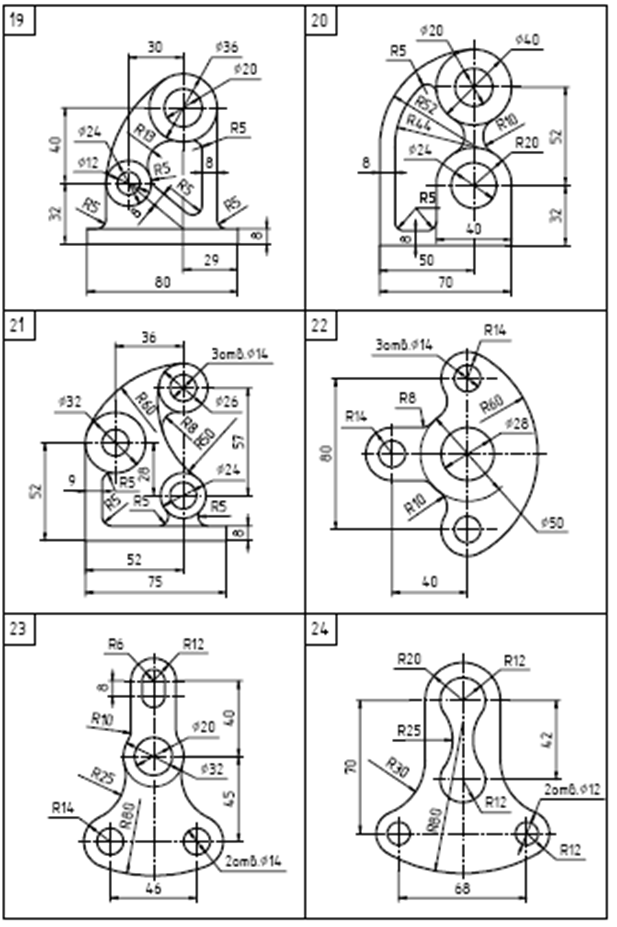
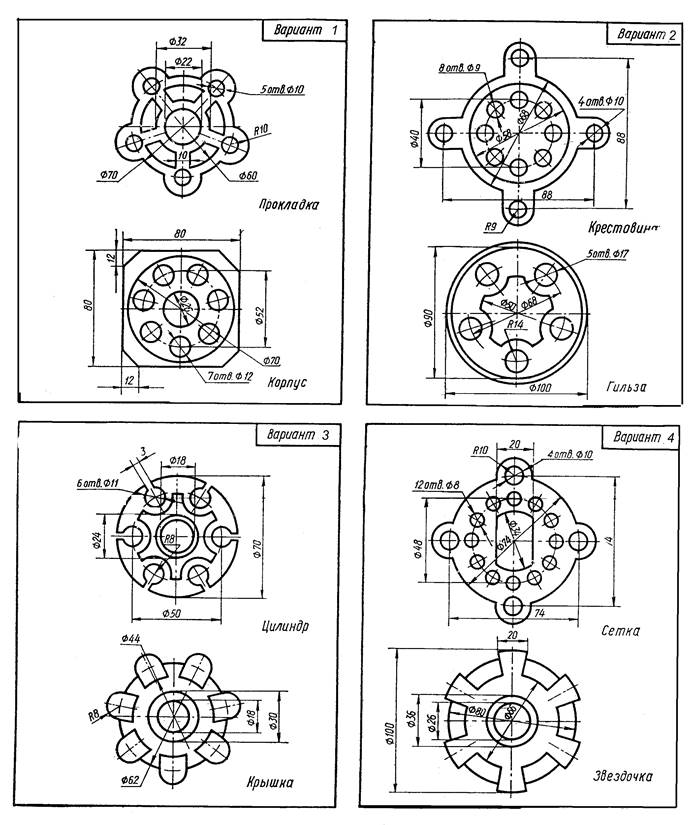
Содержание задания. На листе чертежной бумаги формата А4 или А3 вычертить контур технической детали с построением сопряжений и других геометрических построений. Нанести размеры. Вариант задания соответствует порядковому номеру фамилии студента в групповом журнале и выбирается по табл. Масштаб изображения при выполнении задания выбрать самостоятельно в зависимости от размеров технической детали и размеров используемого формата.
Методические указания к выполнению задания. Приступая к выполнению чертежа, необходимо:
- изучить тему «Геометрические построения на чертежах»;
- из табл. по своему порядковому номеру в журнале группы выбрать вариант;
- произвести анализ графического состава предложенного для построения контура, т.е. определить, какие геометрические построения необходимо применить в данном случае и разбить их на отдельные этапы. Все построения вначале выполняются тонкими линиями, а затем контуры элементов детали обводятся сплошной толстой основной линией. Геометрические построения на чертеже можно не сохранять. Точки сопряжения необходимо сохранить обязательно в виде окружностей радиусом 0,6…1,0 мм.
Образец выполнения задания приведен на рис. 7
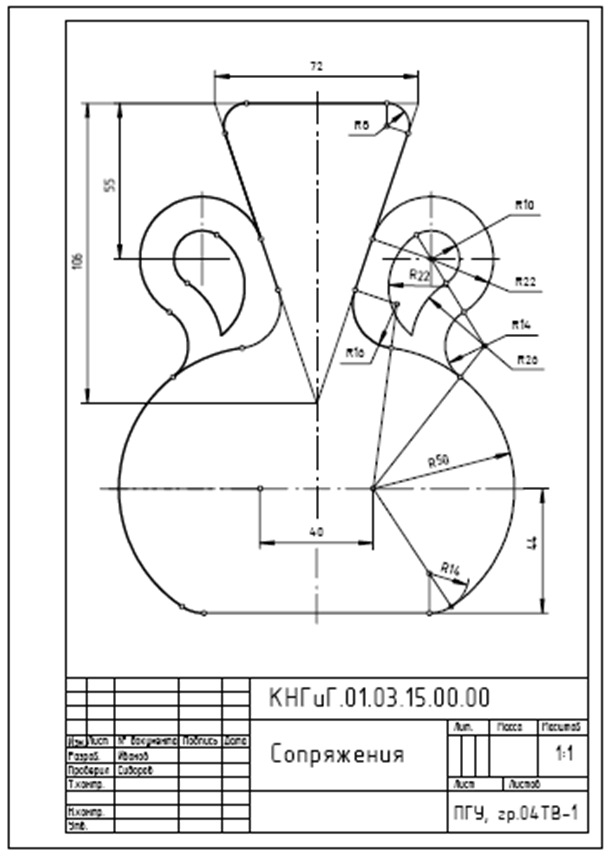
Рисунок 9
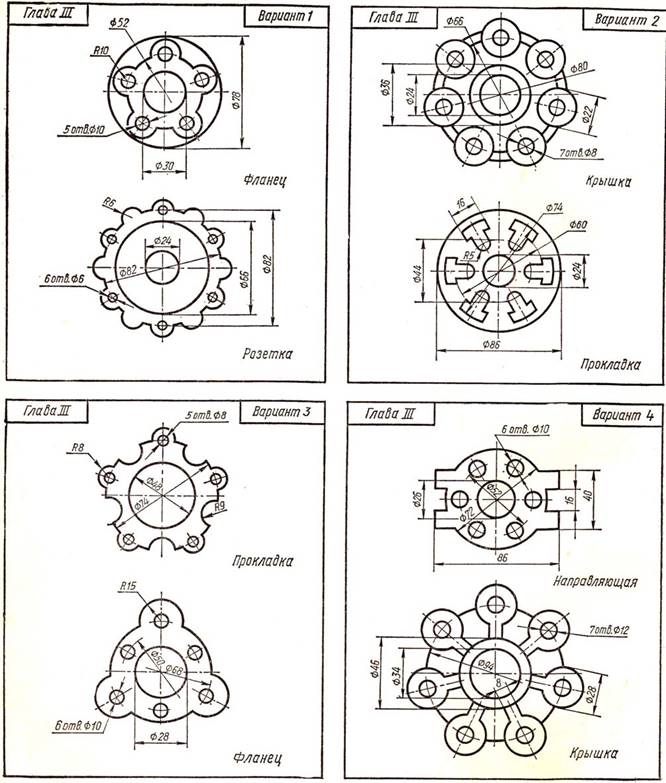
Варианты заданий
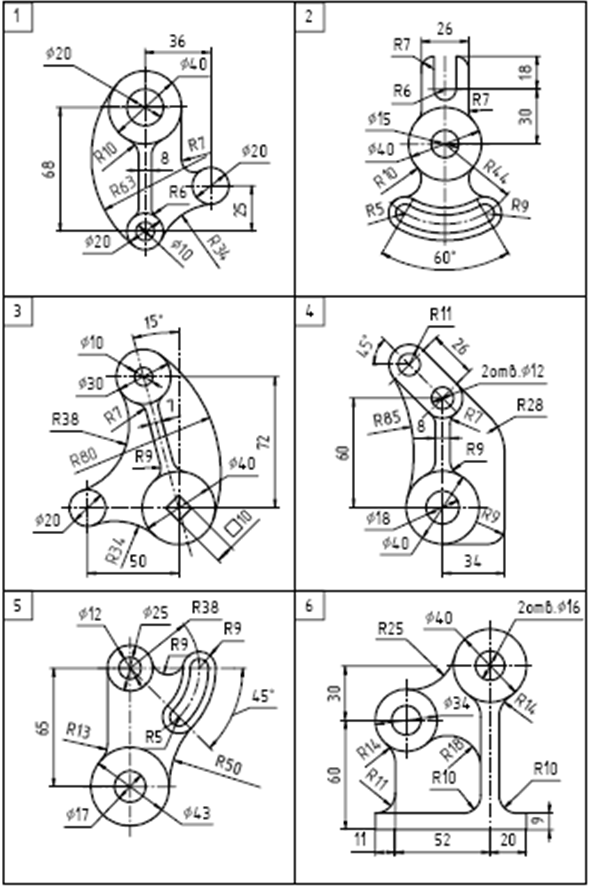
4 КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как разделить окружность на 3 равные части?
2. Как разделить окружность на 6 равных частей?
3. Как разделить окружность на 8 частей?
4. Как построить внешнее сопряжение?
5. Как построить внутреннее сопряжение?
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.