Практическая работа специальности 15.02.05. «Техническая эксплуатация оборудования в торговле и общественном питании»

Министерство образования, науки и молодежной политики Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение

Краснодарского края

«Армавирский механико – технологический техникум»

Методическое пособие

для проведения

практического занятия

на тему:

«ИЗОБРАЖЕНИЯ ПЛОСКОСТИ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ»

по дисциплине: «Инженерная графика»

для студентов 2 курса

спец. 19.02.03, 19.02.06, 19.02.08, 19.02.09

очного и заочного отделения

Разработал преподаватель: Е.В. Игнатова

2016

1     ЦЕЛЬ РАБОТЫ:

- ознакомиться с изображениями плоскости на комплексном чертеже.

2 ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ

1.1 Определение положения плоскости

Для произвольно расположенной плоскости проекции ее точек заполняют все три плоскости проекций. Поэтому не имеет смысла говорить о проекции всей плоскости целиком, нужно рассматривать лишь проекции таких элементов плоскости, которые ее определяют.

На основании законов стереометрии плоскость определяется, когда известны принадлежащие ей:

1) три точки, не лежащие на одной прямой;

2) прямая и точка, не находящаяся на этой прямой;

3) две пересекающиеся прямые;

4) две параллельные прямые.

Итак, плоскость будет считаться заданной, если имеется на эпюре одна из перечисленных выше комбинаций элементов, определяющих данную плоскость (рис. 35 случаи 1, 2, 3, 4).

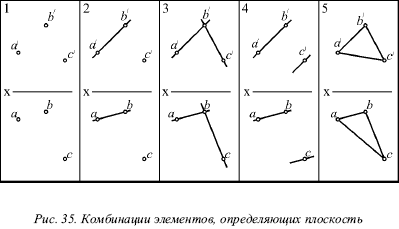Все четыре способа задания плоскости равнозначны, так как легко имея одну комбинацию элементов, изображенную на рисунке 35 перейти к любой другой.

Если соединить одноименные проекции трех точек А, В и С, определяющих данную плоскость (рис. 35, случай 5), можно получить проекции треугольника ABC, лежащего в этой плоскости. Способ изображения плоскости в виде треугольника, не является принципиально новым, но обладает по сравнению с остальными четырьмя случаями большей наглядностью.

1.2 Следы плоскости

След плоскости Р – это линия пересечения ее с данной плоскостью или поверхностью (рис. 36).

Линию пересечения плоскости Р с горизонтальной плоскостью называют горизонтальным следом и обозначают P_h, а линию пересечения с фронтальной плоскостью – фронтальным следом и обозначаютР_v (рис. 37).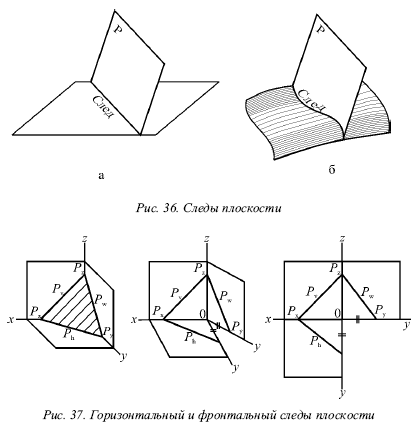

Иногда применяется и профильный след P_w – линия пересечения данной плоскости с профильной плоскостью.

Точки, в которых пересекается плоскость Р с осями проекций, называют точками схода следов. Р_х – точка схода следов на оси х, P_у – на оси у, а Р_z – на оси z (рис. 37). в точке Р пересекаются следы P_h и P_vи т. д.

Следы P_h и P_v плоскости Р являются прямыми, которые и лежат на горизонтальной и фронтальной плоскостях. Они имеют по одной из своих проекций, которые совпадают с осью х: горизонтальный след P_h – фронтальную, а фронтальный P_v– горизонтальную проекции.

Любую плоскость Р можно задать на эпюре с помощью указания положения двух ее следов – горизонтального и фронтального (рис. 38).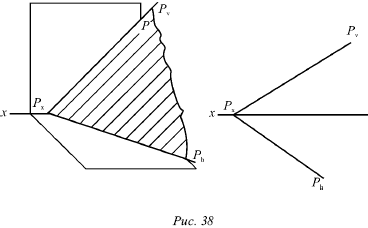

Следы P_h и P_v чаще всего изображаются парой пересекающихся или параллельных прямых и поэтому могут определять положение плоскости в пространстве.

1.3 Прямая, лежащая в данной плоскости

Прямая принадлежит плоскости Р в том случае, если любые две ее точки лежат в данной плоскости.

Например, если следы прямой лежат на одноименных следах плоскости, то прямая лежит в этой плоскости (рис. 39).

Рассмотрим построение прямой, лежащей в данной плоскости Р.

Первый способ. Возьмем на следах P_h и P_v по одной точке (рис. 40) и рассмотрим их как следы искомой прямой.

Рассматривая следы прямой, легко построить ее проекции.

Второй способ. Одну проекцию прямой, например горизонтальную 1, можно провести (рис. 40). Точки ее пересечения со следом P_h и осью х определят горизонтальные проекции h и v следов искомой прямой. Если соединить прямой фронтальные проекции h́ и v́ следов, можно получить фронтальную проекцию 1́.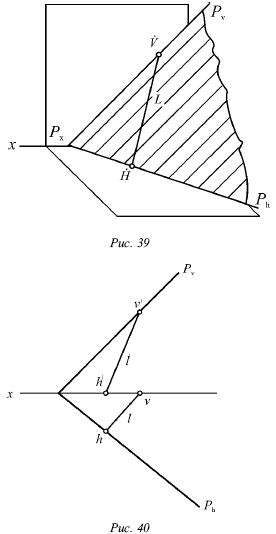

1.4 Горизонтали и фронтали плоскости

Среди прямых, которые лежат в некоторой плоскости, можно выделить два класса прямых, играющих большую роль при решении всевозможных задач. Это прямые, которые называют горизонталями ифронталями.

Горизонталь плоскости Р (рис. 41) – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости. Горизонталь как прямая, параллельная горизонтальной плоскости, имеет фронтальную проекцию ѓ, параллельную оси х.

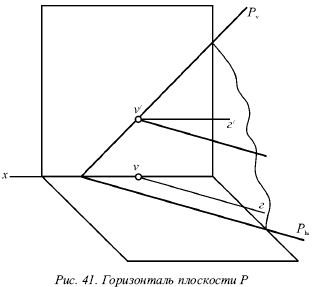
Три прямые – горизонталь Г, ее горизонтальная проекция г и горизонтальный след P_h плоскости Р – параллельны (рис. 42).

Действительно, горизонталь является прямой, параллельной горизонтальной плоскости, и поэтому не имеет горизонтального следа P_h, лежащего с ней в одной плоскости. При этом горизонталь Г не может пересечь свою горизонтальную проекцию г. В противном случае в этой точке пересечения она встречала бы горизонтальную плоскость, что противоречит определению, т. е. все три прямые Г, г и P_h параллельны.

Любая из плоскостей имеет множество горизонталей. Все горизонтали этой плоскости параллельны друг другу вследствие того, что все они параллельны прямой P_h.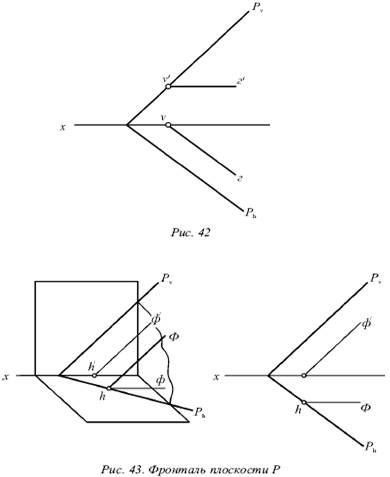

Фронталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости (рис. 43).

Фронталь является прямой, параллельной фронтальной плоскости, и ее горизонтальная проекция ф параллельна оси х.

Фронталь Ф, ее фронтальная проекция ф́ и фронтальный след P_v взаимно параллельны. У каждой плоскости есть бесчисленное множество фронталей. Все фронтали данной плоскости параллельны, за исключением плоскости, параллельной фронтальной плоскости.

1.5 Точка, лежащая в данной плоскости

Если необходимо построить некоторую точку в данной плоскости Р, то нужно предварительно провести в этой плоскости одну из прямых и на ней взять искомую точку.

Если задача обратная, т. е. необходимо узнать, лежит ли данная точка в плоскости Р, то нужно провести через эту точку какую-нибудь прямую, лежащую в этой плоскости. Если такую прямую провести нельзя, то исследуемая точка М не лежит в плоскости Р.

Часто в качестве вспомогательной прямой применяют горизонталь или фронталь, хотя можно применять и прямые общего положения.

Покажем построение в плоскости Р произвольной точки (рис. 44).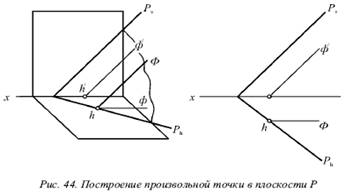

Для выполнения задания необходимо провести любую горизонталь Г этой плоскости и на ней выбрать некоторую точку М. Данная точка принадлежит плоскости, следовательно, задача выполнена.

1.6 Взаимное расположение прямых и плоскостей

1.6.1 Взаимное расположение двух плоскостей

Для двух плоскостей возможны следующие варианты взаимного расположения: они параллельны или пересекаются по прямой линии.

Из стереометрии известно, что две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Это условие называют признаком параллельности плоскостей.

Если две плоскости являются параллельными, то они пересекают какую-то третью плоскость по параллельным прямым. Исходя из этого у параллельных плоскостей Р и Q их следы являются параллельными прямыми (рис. 50).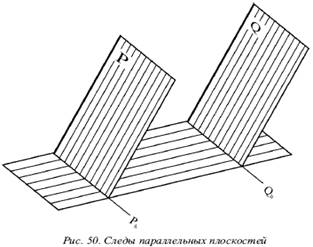

В случае, когда две плоскости Р и Q параллельны оси х, их горизонтальные и фронтальные следы при произвольном взаимном расположении плоскостей будут параллельными оси х, т. е. взаимно параллельными. Следовательно, при таких условиях параллельность следов является достаточным признаком, характеризующим параллельность самих плоскостей. Для параллельности подобных плоскостей нужно убедиться в параллельности и профильных их следов P_w и Q_w. Плоскости Р и Q на рисунке 51 параллельны, а на рисунке 52 они не параллельны, несмотря на то что P_v || Q_v, и P_h у || Q_h.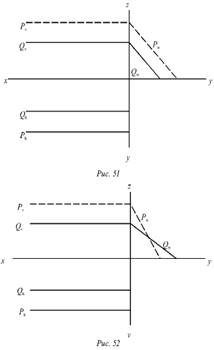

В случае, когда плоскости параллельны, горизонтали одной плоскости параллельны горизонталям другой. Фронтали одной плоскости при этом должны быть параллельными фронталям другой, так как у этих плоскостей параллельны одноименные следы.

Для того чтобы построить две плоскости, пересекающиеся между собой, необходимо найти прямую, по которой пересекаются две плоскости. Для построения этой прямой достаточно найти две точки, принадлежащие ей.

Иногда, когда плоскость задана следами, найти данные точки легко с помощью эпюра и без дополнительных построений. Здесь известно направление определяемой прямой, и ее построение основывается на использовании одной точки на эпюре.

1.6.2 Прямая, параллельная плоскости

Может быть несколько положений прямой относительно некоторой плоскости.

1. Прямая лежит в некоторой плоскости.

2. Прямая параллельна некоторой плоскости.

3. Прямая пересекает данную плоскость.

Рассмотрим признак параллельности прямой и плоскости. Прямая является параллельной плоскости, когда она параллельна любой прямой, лежащей в этой плоскости. На рисунке 53 прямая АВ параллельна плоскости Р, так как она параллельна прямой MN, которая лежит в этой плоскости.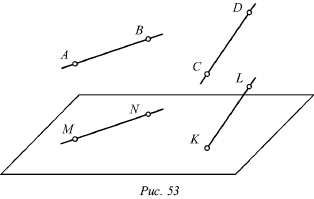

Когда прямая параллельна плоскости Р, в этой плоскости через какую-либо ее точку можно провести прямую, параллельную данной прямой. Например, на рисунке 53 прямая АВ параллельна плоскости Р. Если через точку М, принадлежащую плоскости Р, провести прямую NM, параллельную АВ, то она будет лежать в плоскости Р. На том же рисунке прямая CD не параллельна плоскости Р, потому что прямая KL, которая параллельна CD и проходит через точку К на плоскости Р, не лежит в данной плоскости.

                           1.6.3 Прямая, пересекающая плоскость

Для нахождения точки пересечения прямой и плоскости необходимо построить линии пересечения двух плоскостей. Рассмотрим прямую I и плоскость Р (рис. 54).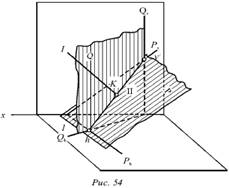

Рассмотрим построение точки пересечения плоскостей.

Через некоторую прямую I необходимо провести вспомогательную плоскость Q (проецирующую). Линия II определяется как пересечение плоскостей Р и Q. Точка К, которую и требуется построить, находится в пересечение прямых I и II. В этой точке прямая I пересекает плоскость Р.

В данном построении основным моментом решения является проведение вспомогательной плоскости Q, проходящей через данную прямую. Можно провести вспомогательную плоскость общего положения. Однако показать на эпюре проецирующую плоскость, используя данную прямую, проще, чем провести плоскость общего положения. При этом через любую прямую можно провести проецирующую плоскость. На основании этого вспомогательная плоскость выбирается проецирующей.

1.6.4 Прямая, перпендикулярная плоскости

Прямая и плоскость перпендикулярны, если на плоскости можно найти две пересекающиеся прямые, перпендикулярные исходной прямой. В качестве подобной пары контрольных прямых легче всего рассматривать следы плоскости P_h и P_v (рис. 55). Это вызвано тем, что прямой угол между перпендикуляром к плоскости и следом P_h дает проекцию на горизонтальную плоскость без искажения, а угол между перпендику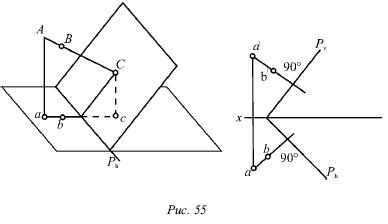и следом Р_v проецируется на фронтальную плоскость V.

Итак, признак перпендикулярности можно задать, используя прямую и плоскость на эпюре.

Прямая является перпендикулярной плоскости, когда проекции прямой перпендикулярны одноименным следам плоскости.

2     ЗАДАНИЕ

1.Изучить теоретическую часть

2 Выполнить графическую работу в тетради

По координатам вершин А,В,С построить комплексный чертеж треугольника и определить его положение относительно плоскостей проекций.

3 ТЕСТИРОВАНИЕ ПО ТЕМЕ «ПРОЕЦИРОВАНИЕ ПЛОСКИХ ФИГУР»

  Вариант 1

1.Проецированием называют 
А. процесс построения разреза, 
В. процесс построения предмета, 
С. процесс построения сечения, 
D. процесс построения разверток.

2. Какое проецирование называется параллельным? 
А. если у прямой и плоскости нет общих точек, 
В. если у прямой и плоскости общая точка, 
С.если прямые линии, направлены в разные стороны, 
D.если проецирующие плоскости перпендикулярны. 

3 След плоскости Р – это

А- фигура, все точки которой лежат на двух плоскостях, 

В-линия пересечения ее с данной плоскостью или поверхностью

С- плоскость, параллельная  плоскости проекций

D- процесс построения предмета

4. Кривая, представляющая собой параллельнуюпроекции окружности, является
замкнутой линией - ее называют 
А. эллипсом, 
В. прямоугольником, 
С. кругом, 
D. сопряжением. 

5. Даны изображения фигуры ABC:

Косоугольная проекция треугольника АВС на плоскость проекций H дана на изображении…

Верный ответ укажите выбором соответствующей буквы из списка:

1.     A     C     B

Вариант2

1.     .Плоской фигурой называют 
А. фигуру, все точки которой лежат на двух плоскостях, 
В. фигуру, все точки которой лежат на одной плоскости, 
С. фигуру, все точки которой не лежат на одной плоскости, 
D. плоскость, параллельную плоскости проекций. 

2.     Плоскость, перпендикулярную к плоскости проекции называют 
А. проецирующей плоскостью, 
В. секущей плоскостью, 
С.плоскостью уровня, 
D.изображающей плоскостью. 

3.     Плоскостью общего положения называется плоскость

А- не параллельная и не перпендикулярная ни одной плоскости проекций.

В- плоскость, параллельную плоскости проекций. 

С- плоскость ,перпендикулярную плоскости проекций

4.     Даны изображения фигуры ABC:

Косоугольная проекция треугольника АВС на плоскость проекций H дана на изображении…

Верный ответ укажите выбором соответствующей буквы из списка:

A     B     C     D

5.     Плоскость проекций, обозначаемая на чертеже H , называется…

- A. Фронтальной плоскостью проекций

- B. Горизонтальной плоскостью проекций

 - C. Профильной плоскостью проекций

Ваша оценка:

 - 5 баллов (отлично), если вы ответили без ошибок;

 - 4 балла (хорошо), если вы допустили одну ошибку;

 - 3 балла (удовлетворительно) если вы допустили две ошибки.

Скачано с www.znanio.ru