Практическая работа специальности 15.02.05. «Техническая эксплуатация оборудования в торговле и общественном питании»

Министерство образования и науки Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение

Краснодарского края

«Армавирский механико – технологический техникум»

Методическое пособие

для проведения

практического занятия   

на тему:

«РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ ГЕОМЕТРИЧЕСКИМ СПОСОБОМрактическое занятие № 7»  

по дисциплине: «Техническая механика»

для студентов 2 курса 

15.02.05

Разработал преподаватель: Е.В. Игнатова

2016

1 ЦЕЛЬ РАБОТЫ

Знать:

- способы сложения двух сил и разложение силы на составляющие;

- геометрический способ определения равнодействующей силы;

- условия равновесия плоской сходящейся системы сил.

Уметь:

- определять равнодействующую системы сил;

- решать задачи на равновесие  геометрическим способом.

2 ДЛЯ ЗАЧЕТА РАБОТЫ НЕОБХОДИМО:

- изучить теоретический материал с помощью  методического пособия;

- по варианту задания выполнить построения  для  определения равнодействующей плоской системы сходящихся сил;

- ответить на контрольные вопросы.

3 КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

         3.1 Равнодействующая сходящихся сил

Система сил, линия действия которых пересекаются в одной точке, называется сходящейся (чертеж 1).

Чертеж 1

Равнодействующую двух пересекающихся сил можно опреде­лить с помощью параллелограмма или треугольника сил (4-я ак­сиома) (чертеж 2).

Чертеж 2

Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему.  Образуется многоугольник сил (чертеж 3). Вектор равнодействующей силы соединит начало первого вектора с концом  последнего.

При графическом способе определения равнодействующей век­торы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Чертеж 3

Вектор равнодействующей направлен навстречу векторам сил слагаемых. Такой способ получения равнодействующей называют геометрическим.

3 а м е ч а н и е. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствую­щим векторам сил.

3.2 Порядок построения многоугольника сил

1.  Вычертить векторы сил заданной системы в некотором мас­штабе один за другим так, чтобы конец предыдущего вектора со­впадал с началом последующего.

2.   Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоуголь­нике меняется вид фигуры. На результат порядок вычерчивания не влияет.

3.3 Условие равновесия плоской системы сходящихся сил

При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

4 ПРИМЕР  ВЫПОЛНЕНИЯ  ЗАДАНИЯ

Определить равнодействующую плоской системы сходящихся сил геометрическим способом.

Дано:

F₁=10кН                α₁=30˚

F₂=15кН                α₂=60˚

F₃=12кН                α₃=120˚

F₄ = 8кН                α₄=180˚

F₅ = 8кН                α₅=300˚

Решение:

С помощью транспортира в масштабе 2 мм = 1кН строят много­угольник сил (чертеж 4). Измерением определить  модуль равно­действующей силы и угол наклона ее к оси Ох.

Чертеж 4

Результаты расчетов не должны отличаться более чем на 5 %:

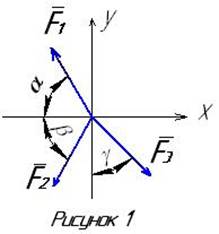
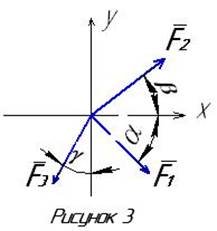
5  ВАРИАНТЫ ЗАДАНИЙ

6 КОНТРОЛЬНЫЕ    ВОПРОСЫ

1.     Какая система сил называется сходящейся?

2.     Как определить равнодействующую двух пересекающихся сил геометрическим способом?

3.     Условие равновесия плоской системы сходящихся сил.

4.     Какой порядок построения многоугольника сил?

5.     Как  выбирается масштаб при построении равнодействующей системы сходящихся сил?