Практикалық жұмыс

Сабақ 1: Арифметикалық  прогрессия

Тапсырма 1:

Бос орындарды толтырыңыз.

Арифметикалық прогрессияның, арифметикалық прогрессия айырмасының анықтамаларын беріңіз.

Тапсырма 2:

Тізбек бірнеше алғашқы мүшелерімен берілген. Олардың қайсысы – арифметикалық прогрессия?

а) 1; 2; 3; 5;…         б) 1; 2; 4; 8;…              в) 1; 3; 5; 7;…                        г).

Тапсырма 3:

Бос орындарды толтырыңыз:

а_n-1; a_n; a_n+1 сандары – арифметикалық прогрессияның  тізбектей орналасқан кез келген үш мүшесі.

Тапсырманы орындаңыз:

Тапсырма 4:         k-ны табыңыз, егер:

а)      k+1; 2k+1; 13 - арифметикалық прогрессияның  тізбектей орналасқан кез келген үш мүшесі.

б)      5; k; k²-8 - арифметикалық прогрессияның тізбектей орналасқан кез келген үш мүшесі.

Тапсырма: Бос орындарды толтырыңыз. Тапсырманы орындап, жұп өз үлестірмесін келесі жұпқа тексеруге береді, осылайша, үлестірме дөңгелене ауысады. Тексеретін жұптар плюс немесе минус таңбасын қояды. Үлестірме өз иесіне қайта келгенде, жұптар өз қателерін түсіндіреді. 

Анықтама. Тізбектің әрбір мүшесі алдыңғы мүшесіне бірдей тұрақты санды қосқанда пайда болған тізбекті  арифметикалық прогрессия деп аталады.

Анықтама. Қосылатын тұрақты сан арифметикалық прогрессияның айырмасы деп аталады және d әрпімен белгіленеді.

Арифметикалық прогрессияның екінші, үшінші, төртінші және бесінші мүшелерін бірінші мүшесі  және айырмасы d арқылы өрнектеп жазыңыз.

 …………

………….

………….

………….

………………………………………

 –ті  және d жазғаннан кейін, нені байқадыңыз?

n-ші мүшесінің формуласын қорытыңыз.

…………………

Оқушылар бос орындарды толтыру арқылы арифметикалық прогрессияның n –ші мүшесінің формуласын өздері қорытып шығарады

Арифметикалық прогрессия. Арифметикалық прогрессияның n-ші мүшесінің формуласы

Арифметикалық прогрессия деп a, d параметрлері мен a₁ = a, a_n = a_n – 1 + d, n = 2, 3,… заңдылығы арқылы берілген сандар тізбегін айтамыз. d параметрі берілген арифметикалық прогрессияның айырымы деп аталады. Мысалы, келесі тізбек арифметикалық тізбек болып саналады: 0; 3; 6; 9; 12; …; 3(n – 1);… Мұнда a= 0 және d = 3.

Бастапқы мәні а-ға және айырымы d-ға тең арифметикалық прогрессияның n-ші мүшесінің формуласы: a_n =a₁ + d(n – 1).

Мысалы, егер арифметикалық прогрессияда a = 12 және d = 5, онда a₂ = 12 + 5(2 – 1) = 17, a₃ = 12 + 5(3 – 1) = 22, a₄ = 12 + 5(4 – 1) = 27. Осылай жалғастыра отырып, ізделінген арифметикалық прогрессияны алуға болады: 12; 17; 22; 27; …; 12 + 5(n – 1);…

Егер арифметикалық прогрессияның айырымы d > 0 болса, онда өспелі сандар тізбегі болып табылады.

Егер арифметикалық прогрессияның айырымы d < 0 болса, онда кемімелі сандар тізбегі болып табылады.

Егер арифметикалық прогрессияның айырымы d = 0 болса, онда тұрақты сандар тізбегі болып табылады.

Арифметикалық прогрессияның қасиеті. Арифметикалық прогрессияның қатарлас үш мүшесінің ортаңғысы екі шеткі мүшелерінің арифметикалық орташасына тең. Басқаша айтқанда, сандар тізбегінің кез келген a_n (n ≥ 2) мүшесін келесідей жазуға болады:

Мұндай сандар тізбектері арифметикалық прогрессия деп аталады.

Жұптық жұмыс

Задание 1. Найдите наибольший член последовательности, заданной формулой n-го члена:

 а_n=10 + 9n -2n²

Задание 2. Найдите наименьший член последовательности, заданной формулой n-го члена:

 а_n=n² - 17n + 21

Задание 3. Напишите первые пять членов последовательности (в_n) _, заданной рекуррентно:

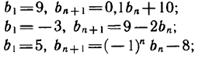
Задание 4. Воспользуйтесь формулой и напишите четыре члена последовательности, если  =11,

 =

Жеке жұмыс

Задание 2. Существуют ли члены последовательности (), заданной формулой = n³ - n + 2, которые при делении на 6 дают в остатке 4?

Задание 3. Напишите первые пять членов последовательности (в_n) _, заданной рекуррентно:

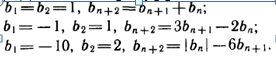
Сабақ 2

Арифметикалық прогрессияның  алғашқы n мүшесінің қосындысын  арқылы белгілейік.

Осы қосындынының  қосылғыштарын өсу ретімен және кему ретімен жазайық:

+…+

Осы екі теңдікті мүшелеп қосайық:

Егер  берілмесе, алғашқы n мүшесінің қосындысын қалай табамыз?

1. Төменгі формуламен берілген тізбектің алғашқы қырық мүшесінің қосындысын табыңыз:

2. 4; 5,5;… арифметикалық прогрессияның алғашқы отыз мүшесінің қосындысын табыңыз.

1)Find the sum of the first 1000 terms of the arithmetic series 3+7+11+15….  

2) A worker  earned $35000 at the beginning  of the school year. She estimates that she  will receive $1750 step increase each year for the next 20 years. How much will she have earned in total after she has worked 20  years?

3)Expand  (490)  b)  

4)Find the sum of each arithmetic series given that

a) the series is: 5+17+29+….+581+593+605

b) there are 200 terms in the series:  -25+(-17)+(-9)+….

c) the series is: 17+22+27+…+387

Тапсырма 1. a)  – арифметикалық прогрессия. Оның екінші мүшесі 2-ге, ал төртінші мүшесі 6-ға тең. Осы прогрессияның алтыншы мүшесін табыңыз.

b) Егер  болса, арифметикалық прогрессияның бірінші мүшесі мен айырмасын анықтаңыз.

Тапсырма 2.a) Арифметикалық прогрессияның бірінші мүшесі 10-ға, ал айырмасы 12-ге тең болса, алғашқы 16 мүшесінің қосындысын есептеңіз.

 b)  – арифметикалық прогрессия. d= 6;  = 340. Табу керек және  .

Бағалау критерийлері:

Арифметикалық прогрессияның  жалпы мүшесінің формуласын біледі;

Берілген элементтер бойынша арифметикалық прогрессияның

кез келген мүшесін табады;

Алғашқы n мүшелерінің қосындысының  формуласын  біледі;

Алғашқы n мүшелерінің қосындысының  формуласын  қолданады;