
Выступление на заседании МО учителей естественно-научного цикла «Еще раз о простых числах».
«Математики уже давно тщетно пытаются найти закономерности
в последовательности простых чисел, но у меня есть
основания полагать, что эта тайна, в которую человеческий разум
никогда не сможет проникнуть». (Леонард Эйлер)
В современном мире интерес к простым числам не ослабевает. Ведется поиск простых чисел с большим количеством цифр. Самая распространенная область применения таких чисел – это шифрование и криптография. Таким вопросам в настоящее время уделяется большое внимание. Откуда берутся простые числа, на каких местах в натуральном ряду они стоят, почему с продвижением по ряду их становится меньше? Поможет нам ответить на эти вопросы теория распределения простых чисел. «Оцифровывание» нашей жизни сегодня это уже необратимый процесс. Сегодня я вслед за великим Пифагором, утверждаю, что числа правят миром. А знать о числах больше это интересно и важно.
Хочется найти ответы на вопросы:
1)как определять «простоту» любого натурального числа, используя для этого не только определение, но и их свойства;
2)найти способ для расширения области простых чисел за рамки школьного учебника;
3)сделать попытку найти общее свойство всех элементов множества простых чисел, несмотря на то что это множество не подчиняется каким-либо закономерностям.
Над этим вопросом работали и Эратосфен, и Катальди, и Лебег, и Гаусс, и Эйлер, и Чебышев, и Дирихле, и Риман и многие другие. На заре веков Пифагор искренне верил, что «числа правят миром». С момента знакомства с натуральным рядом и особенно его составляющей-множеством простых чисел меня не покидает желание узнать больше о их свойствах, раскрыть тайну появления этих чисел, причину скоплений простых чисел на одном участке множества N и их полное отсутствие на другом. Не покидает желание найти хоть какую-нибудь закономерность, связанную с простыми числами, научиться определять «простоту» числа за минимальное число шагов. Имеются два главных факта о распределении простых чисел. Первый: простые числа, при своём таком простом определении и при своей роли кирпичиков, из которых строятся все натуральные числа, являются самыми капризными и упрямыми из всех объектов, вообще изучаемых математиками. Они растут среди натуральных чисел как сорная трава, не подчиняясь, кажется, ничему, кроме случая, и никто не может предсказать, где взойдет ещё одно простое, а, увидев число, – определить, простое оно или нет. Другой факт озадачивает ещё больше, так как он состоит в прямо противоположном утверждении, а именно: простые числа демонстрируют удивительную регулярность, они подчиняются законам, и притом с почти педантичной точностью.
Извечный философский вопрос - Что первично, курица или яйцо? Решается просто по аналогии - Что первично, ствол дерева или его листья? Ответ однозначен - Первичны корни дерева, питающие ствол, чтобы появились листья. Из всех трех составляющих дерева постоянно виден только ствол, тогда как наиглавнейшими являются листья и невидимые корни. Так обстоит все в Природе. Изучая свойства чисел мы учимся видеть невидимые корни всех явлений в природе.
История вопроса .
Никто точно не знает, в каком обществе стали впервые рассматривать простые числа. Их изучают так давно, что у ученых нет записей тех времен. Есть предположения, что некоторые ранние цивилизации имели какое-то понимание простых чисел, но первым реальным доказательством этого являются египетские записи на папирусах, сделанные более 3500 лет назад.
Древние греки, скорее всего, были первыми, кто изучал простые числа как предмет научного интереса, и они считали, что простые числа важны для чисто абстрактной математики. Теорему Евклида по-прежнему изучают в школе.
После греков серьезное внимание простым числам снова уделяли в XVII веке. С тех пор многие известные математики внесли важный вклад в наше понимание простых чисел. Пьер де Ферма совершил множество открытий и известен благодаря Великой теореме Ферма, 350-летней проблеме, связанной с простыми числами и решенной Эндрю Уайлсм в 1994 году. Леонард Эйлер доказал много теорем в XVIII веке, а в XIX веке большой прорыв был сделан благодаря Карлу Фридриху Гауссу, Пафнутию Чебышёву и Бернхарду Риман. Кульминацией всего этого стала до сих пор не решенная гипотеза Римана, которую часто называют важнейшей нерешенной задачей всей математики. Гипотеза Римана позволяет очень точно предсказать появление простых чисел, а также отчасти объясняет, почему они так трудно даются математикам. Простые числа на протяжении многих столетий приковывали к себе внимание великих людей, чьи имена указаны выше. Есть в этих числах магнетизм простоты и загадочность неподчинения закономерностям. Вот и я, обычный пятиклассник, попался на эту «удочку». Мне интересно прикоснуться к тайне, которая до сих пор не разгадана. Хорошо было бы, если все простые числа можно было сосчитать! Но эта проблема до сих пор остается не решенной. Как сказал греческий геометр Евклид: самого большого простого числа не существует.
Определение и примеры простых чисел.
Определение. Простое число -это натуральное число, которое имеет ровно два различных натуральных делителя: единицу и само себя. Все остальные числа, кроме единицы, называются составными. Таким образом, все натуральные числа, большие единицы, разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел.
Основная теорема арифметики утверждает, что каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей. Таким образом, простые числа -- элементарные «строительные блоки» натуральных чисел.
Применение. Люди изменили окружающий нас мир, построили невероятные города, и разработали впечатляющие технологии, которые привели к появлению современного мира. Спрятанный под внешней оболочкой планеты, где мы живем, невидимый мир состоит из чисел, последовательностей и геометрии. Математика - это код, который придает смысл всей вселенной.
3. Простые числа и вопрос «Причем тут
цикады?»  В
лесах Теннеси этим летом часть кода, о котором идет речь, в прямом смысле слова
выросла прямо из земли. Каждые 13 лет примерно на 6 недель хор насекомых
очаровывает всех, кто становится свидетелем этого редкого природного явления. Выживание
этих цикад, которых можно найти только в восточных регионах северной Америки,
зависит от странных свойств некоторых из самых фундаментальных чисел в
математике - простых чисел. Цикады появляются здесь периодически, но их
появление всегда происходит в те года, числа которых состоят из простых чисел.
В случае с выводком, который появился вокруг Нэшвилле в этом году, то с момента
их прошлого появления прошло 13 лет. Выбор 13-детнего цикла не кажется
случайным. В разных частях северной Америки есть еще два выводка, жизненный
цикл которых также составляет 13 лет. Они возникают в разных регионах и в
разные года, но между появлениями этих живых существ проходит ровно 13 лет.
Вдобавок, существует еще 12 выводков насекомых, которые появляются через каждые
17 лет.
В
лесах Теннеси этим летом часть кода, о котором идет речь, в прямом смысле слова
выросла прямо из земли. Каждые 13 лет примерно на 6 недель хор насекомых
очаровывает всех, кто становится свидетелем этого редкого природного явления. Выживание
этих цикад, которых можно найти только в восточных регионах северной Америки,
зависит от странных свойств некоторых из самых фундаментальных чисел в
математике - простых чисел. Цикады появляются здесь периодически, но их
появление всегда происходит в те года, числа которых состоят из простых чисел.
В случае с выводком, который появился вокруг Нэшвилле в этом году, то с момента
их прошлого появления прошло 13 лет. Выбор 13-детнего цикла не кажется
случайным. В разных частях северной Америки есть еще два выводка, жизненный
цикл которых также составляет 13 лет. Они возникают в разных регионах и в
разные года, но между появлениями этих живых существ проходит ровно 13 лет.
Вдобавок, существует еще 12 выводков насекомых, которые появляются через каждые
17 лет.
Вы можете принять эти числа за совершенно случайные. Но это очень любопытно, что не существует цикад с циклом жизни, равным 12, 14, 15, 16 или 18 лет. Однако, посмотрите на этих цикад глазами математика и картина начинает проясняться. Потому, что числа 13 и 17 оба являются неделимыми, это дает цикадам эволюционные преимущества между другими животными, циклы жизни которых являются периодическими, а не простыми числами. Возьмем, к примеру, хищника, который появляется в лесах каждые шесть лет. Тогда восьми- или девятилетние циклы жизни цикад будут совпадать с циклами жизни хищников, в то время как семилетние циклы жизни будут совпадать с циклом жизни хищника намного реже.
Согласно одной теории, у цикады имеется паразит, также обладающий длинным жизненным циклом. Цикада, естественно, стремится избавиться от паразита. Если паразит обладает жизненным циклом продолжительностью, скажем 2 года, то цикада стремится избежать жизненного цикла, продолжительность которого в годах делится на 2, так как в противном случае цикада, появляясь из-под земли, и паразит регулярно встречались бы. Аналогично, если бы паразит обладал жизненным циклом продолжительностью 3 года, то цикада стремилась бы избегать жизненных циклов, продолжительность которых в годах выражалась числом, кратным 3. Следовательно, чтобы избежать совпадений с паразитом, лучшей стратегией для цикады было бы иметь жизненный цикл, длящийся простое число лет. Так как ни одно целое число (кроме 1 и 17) не делит число 17, Magicicada septendecim очень редко встречается со своим паразитом. Если продолжительность жизненного цикла паразита составляет 2 года, то цикада встречается с ним только раз в 34 года, а если продолжительность жизненного цикла паразита больше, например, составляет 16 лет, то его встреча с цикадой происходит лишь раз в 272 (= 16·17) года.
«Реванш» для паразита возможен только в двух случаях: при его годичном жизненном цикле и при жизненном цикле продолжительностью 17 лет. Маловероятно, однако, что паразит выживет на протяжении 17 своих поколений подряд, так как первым 16 поколениям будет не на ком паразитировать. С другой стороны, чтобы достичь 17-летней продолжительности жизненного цикла, поколениям паразита необходимо пройти в своей эволюции 16-летний жизненный цикл. Это означало бы, что на каком-то этапе эволюции паразит и цикада не встречались бы на протяжении 272 лет! И в том, и в другом случае большой жизненный цикл продолжительностью в простое число лет способствуют выживанию цикады.
Возможно, именно этим и объясняется, что пресловутый паразит так никогда и не был найден! В гонке на выживание с цикадой паразит, по-видимому, постоянно увеличивал продолжительность своего жизненного цикла до тех пор, пока не наткнулся на 16-летний барьер. После этого паразит на протяжении 272 лет не мог встретиться со своей жертвой и за это время вымер. В результате появилась цикада с жизненным циклом длиной 17 лет. Необходимость в более продолжительном жизненном цикле для цикады отпала, поскольку паразит более не существовал. Эти насекомые вмешались в математический код, чтобы выжить.
4.Криптография.
Цикады обнаружили пользу использования простых чисел для своего выживания, однако люди поняли, что эти числа являются не только ключом к выживанию, но и огромным количеством строительного материала в математике. Каждое число, по сути, представляет собой совокупность простых чисел, а совокупность чисел составляет математику, а из математики вы получите целый научный мир. Простые числа находят спрятанными в природе, но человечество научилось их использовать. Понимание фундаментального характера этих чисел и использование их свойств людьми, в буквальном смысле поставило их в основу всех кодов, которых охраняют мировые кибер-секреты.
Криптография, благодаря которой наши кредитные карточки остаются в безопасности, когда мы покупаем что-нибудь онлайн, использует те же числа, которые защищают цикад в Северной Америке - простые числа. Каждый раз, когда вы вводите номер своей кредитной карты на вебсайте, вы полагаетесь на то, что простые числа сохранят ваши тайны и информацию о вас в секрете. Для кодирования вашей кредитной карты ваш компьютер получает публичный номер Н с вебсайта, который и будет использоваться для совершения операций с вашей кредитной картой.
Это перемешивает ваши данные так, что закодированное письмо может быть послано через интернет. Вебсайт использует простые числа, на которые делят число Н, чтобы раскодировать послание. Хотя Н является открытым числом, простые числа, из которых оно состоит, являются секретными ключами, которые расшифровывают данные. Причиной, по которой такое кодирование является настолько безопасным, является то, что очень легко перемножить простые числа между собой, но разложить число на простые практически невозможно.
5.Загадки простых чисел.
Простые числа являются атомами арифметики, гидрогеном и оксигеном мира чисел. Но вопреки их фундаментальному характеру, они также являют собой одну из самых больших загадок математики. Потому что, проходя по вселенной чисел практически невозможно предсказать, где вы встретите следующее простое число. Мы знаем, что количество простых чисел уходит в бесконечность, но поиск закономерности появления простых чисел является самой большой загадкой математики. Приз в миллион долларов обещан тому, кто сможет раскрыть тайну этих чисел. Загадка о том, когда первый раз цикады начали пользоваться простыми числами, чтобы выжить является такой же сложной, как и сама загадка простых чисел. Простые числа - «капризны». Таблицы простых чисел обнаруживают большие «неправильности» в распределении простых чисел. Пестрота картины распределения простых чисел увеличивается еще более, если отметить, что существуют пары простых чисел, которые отделены в натуральном ряду только одним числом («близнецы»). Например. 3 и 5, 5 и 7, 11 и 13, 10016957 и 10016959. С другой стороны, существуют пары простых чисел, между которыми много составных. Например, все 153 числа от 4652354 до 4652506 являются составными. За нахождение простых чисел из более чем 100 000 000 и 1 000 000 000 десятичных цифр EFF назначила денежные призы соответственно в 150 000 и 250 000 долларов США.
6.Таблица простых чисел в учебнике 5класса и как её продолжить?
Таблица простых чисел или «кто следующий?» При изучении темы «Простые числа» в 5 классе в учебнике имеется таблица простых чисел, которые встречаются среди натуральных от 1 до 1000. Завершает таблицу число 997. Возникает вопрос: «А есть ли простые числа дальше? Если есть, то как их найти? Больший интерес представляет не само следующее простое число, а способ его выявления.
Задача 1. Ответ на первый вопрос дает сам Евклид, доказывая, что множество простых чисел бесконечно. Простое доказательство этого факта не оставляет никаких сомнений.
Доказательство: Пусть простых чисел ровно k штук, и p1,…,pk – все простые числа.
Возьмем n=p1∙p2∙…∙pk+1.
По предположению, n – составное число, т.к. n> ![]() ,
, ![]()
![]() существует
простое число d: d\n.
существует
простое число d: d\n.
Но очевидно, исходя из вида числа n,
что ![]() ,
, ![]()
![]() получили
противоречие с тем, что p1,…,pk –
все простые числа.
получили
противоречие с тем, что p1,…,pk –
все простые числа.
Из доказанного следует , что после простого числа 997 еще есть бесконечно много простых чисел. Попробуем определить следующее из них. Понятно, что на роль простых претендуют только нечетные числа: 999,1001,1003,1005,1007,1009,1011…
Ясно , что сразу не подходят следующие:
999(кратно 1,999 , 9 -более 2 делителей, составное)
1001(кратно 1,1001, 11-сумма цифр на четных местах равна сумме цифр на нечетных, составное)
1003(кроме 1 и 1003 , делится на 17; составное)
1005(оканчивается на 5, его делители 1,1005,5..;составное)
1007(делители-1,1007,19,..;составное)
1011(делители 1,1011,3-сумма цифр кратна 3, составное)
Остался один претендент -число 1009.Дополнительеная проверка показывает, это число не делится ни на одно из простых чисел от 2 до 97.
1009:97=10,402.. Дальнейшая проверка на делимость 1009 на простые числа большие , чем 97 лишена всякого смысла. Если бы оно делилось, скажем на трехзначное простое число, то результат был бы однозначным, а, следовательно, и это однозначное частное от деления было бы делителем нашего числа, но среди однозначных простых таких не оказалось. Значит, делителями числа 1009 являются только 1 и само число 1009.
Вывод: 1009 – простое!! Таким образом, таблица простых чисел из учебника продолжена.
Полное отсутствие закономерностей во множестве простых чисел и парадоксальное общее их свойство.
Задача 2 Хотелось бы найти хоть какую-нибудь закономерность, которая годится для любого простого числа. Ведь на сегодняшний день за простыми числами закрепилась дурная слава как о числах капризных. Многолетние и многочисленные попытки знаменитых математиков найти общую закономерность появления нового простого числа так и не увенчались успехом. Утверждаю, что для всех простых чисел, больших чем 3, выполняется такое свойство: квадрат простого числа, уменьшенный на 1, делится на 24.
52-1=24; 72-1=48 112-1=120 и т.д. Доказательство: Пусть р-данное простое число.р2-1=(р-1)(р+1) Множитель из первых скобок-число перед нашим простым, во вторых скобках-следующее за ним. р-1,р,р+1 -три последовательных натуральных числа, р-простое большее чем 3,следовательно ,р-нечетно. Значит, р-1 и р+1 кратны 2 и 4, одно из них кратно 3. Поэтому их произведение кратно 3*2*4=24. Ч.Т.Д.
Задача 3 .Случайным образом выбирается число из натурального ряда. Моя цель как можно быстрее и изящнее определить является ли оно простым. Для реальности эксперимента прошу своих одноклассников «обстреливать» меня числами, а я тут же пытаюсь определить его принадлежность множеству простых чисел. Использую калькулятор для того, чтобы техническая сторона дела не погубила идею. Если использовать только определение простого числа, то процесс превращается в непрерывное терзание калькулятора. Для упрощения и ускорения использую признаки делимости на 2,3,5,11, а также необходимое, но недостаточное свойство для простоты числа, описанное в Задаче 2. Например, число 3569.
35692=12737761 35692-1=12737760 1237760:24=530720 Ответ-натуральное число, поэтому есть надежда (но не факт!), что 3569-простое. Уточняем детали с помощью калькулятора. Очевидно, что на 2,3,5,7,11 не делится. При делимости на трехзначный ответ результат-однозначное или двузначное число также должно быть делителем. Но однозначные-не делители. Поэтому осталось проверить делимость на простые максимум до 311. При делении на 83- ответ натуральный. Значит у нашего числа более двух делителей – составное.
Заключение.
Работая над данной темой, пришел к выводу, что простые числа не так просты как кажется. При всей своей доступности тема вместе с тем полна загадок, нераскрытых тайн. Во-первых, мне удалось расширить свои знания в данной области. Я разобрался в вопросе о количестве простых чисел и доказательстве факта о бесконечности этого количества, которое(доказательство)приведено у Евклида. Во – вторых, в моей работе видно, что простые числа выходят далеко за пределы учебника математики. В-третьих, удалось понять и обосновать общее свойство простых чисел, больших чем 3.Более того, проверка показала, что данное свойство работает только в одну сторону:р-простое,р2-1 делится нацело на 24.Обратно-не всегда :24*х+1 не всегда квадрат простого числа(24*2+1=49=72,7-простое, но24*26+1=625=252,25-составное). И, наконец, в-четвертых, применимость простых чисел в жизни - это очень интересно. Не знаю, что больше удивляет и захватывает: криптография и коды или цикады с их жизненным циклом?
IV. Литература
1. Виленкин Н. Я. Функции в природе и технике: Книга для внеклассного чтения 9 – 10 кл. – 2 – е изд., испр. – М.: Просвещение, 1993.
2. Глейзер Г.И. История математики в школе.- М., Просвещение, 1981.
7. Энциклопедический словарь юного математика. Составитель Савин А.П.- М., Просвещение, 1985.
Приложение
(из учебника математики для 5 -го класса). 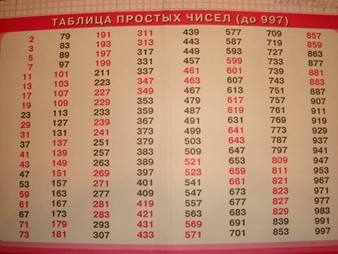
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.