Системы счисления. Перевод чисел из одной системы счисления в другую. 9 класс

Копылова Ирина Андреевна,

учитель информатики  МОУ школа № 13

E-mail: school13@progtech.ru

Цели урока:

1. Познакомиться с системами

счисления.

2. Научиться переводить числа из десятичной системы счисления в другие системы счисления и

наоборот.

Система счисления – это определенные правила записи чисел и связанные с ними способы выполнения вычислений.

Системы счисления бывают:

-     непозиционные

-     позиционные

Непозиционные системы счисления

Значение цифры в записи числа  постоянно и не зависит от ее положения  в числе (от позиции цифры).

Примеры:

1)    единичная система счисления;

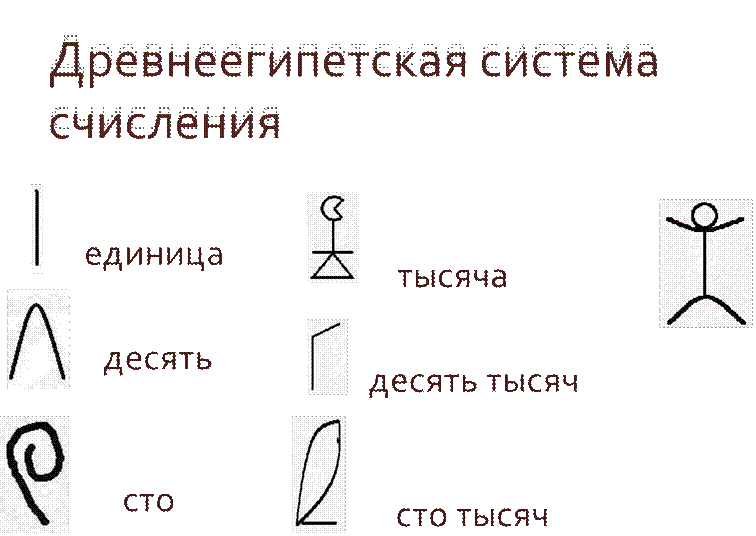
2)   древнеегипетская система счисления;3)  алфавитная система счисления; 4)  римская система счисления.

Единичная система счисления

Для обозначения чисел используется один символ, например черта или точка.

1----------------------------- I

2---------------------------- II

34 – IIII------------------- III

миллион

345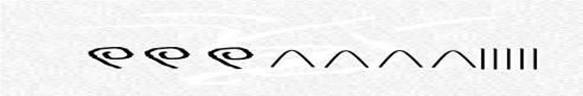     

Алфавитная (славянская) система счисления

1)           для записи чисел использовался буквенный алфавит;

2)          над буквой, обозначающей цифру, ставился специальный знак – «титло»;

3)           алфавитная система счисления была распространена у древних армян, грузин, арабов, евреев и других  народов Ближнего

Востока;

4)          славянская система счисления сохранилась в богослужебных книгах.

Пример славянских цифр

Римская система счисления

Цифры римской системы счисления

                    I      V      X     L      C       D   M

                    1     5     10   50   100        500  1000

Правила записи  римских чисел

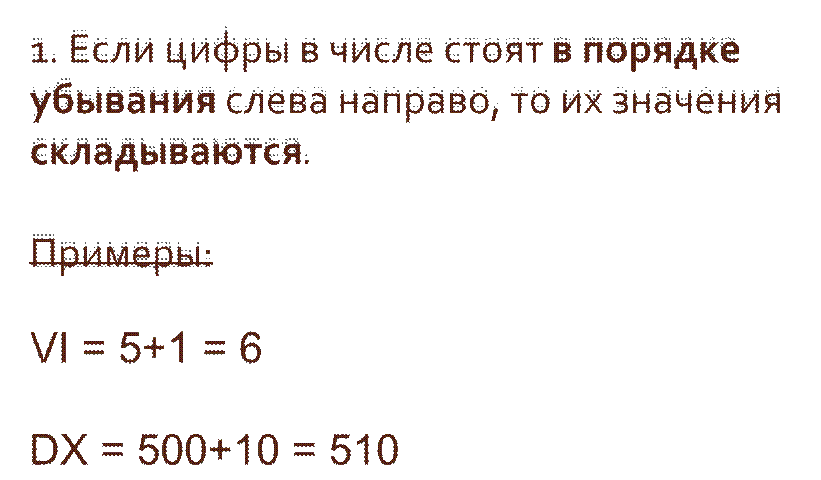
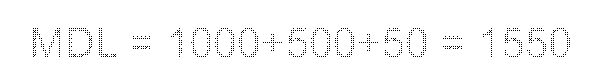MDL = 1000+500+50 = 1550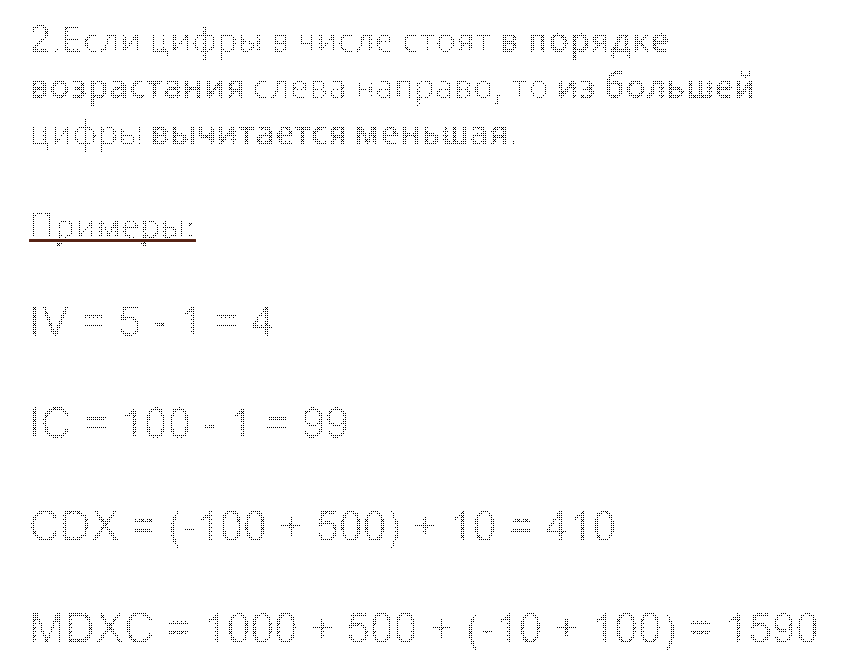

2.Если цифры в числе стоят в порядке возрастания слева направо, то из большей цифры вычитается меньшая.

Примеры:

IV = 5 - 1 = 4

IC = 100 - 1 = 99

CDX = (-100 + 500) + 10 = 410

MDXC = 1000 + 500 + (-10 + 100) = 1590

Недостатки римской системы счисления

—  Трудно записывать большие числа;

—  Нельзя записывать дробные и отрицательные числа;

—  Нет нуля;

—  Очень сложно выполнять арифметические действия.

Римская система счисления сегодня   используется, в основном,  для наименования знаменательных  дат, томов, разделов и глав в книгах.

Позиционные системы счисления

Французский математик Пьер Симон Лаплас (1749-1827) такими словами оценил «открытие» позиционной системы счисления: «Мысль – выражать все числа немногими знаками, придавая им значение по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна.»

Позиционные системы счисления

Значение цифры в записи числа  зависит от ее положения  в числе (от позиции цифры).

Примеры позиционных систем счисления: двоичная, троичная, пятеричная, восьмеричная, десятичная и  др.

Позиционные системы счисления

Десятичная система счисления

Основание: 10

Алфавит: 0,1, 2, 3, 4, 5, 6, 7, 8, 9

Основание – это количество знаков, которое используется для записи чисел.

Алфавит – это набор цифр, из которых состоят числа.

Развернутая форма десятичного числа

5 – коэффициент числа

10 – основание

2,1,0 – степени при основании

Перевод десятичных чисел в двоичную систему счисления

Правило.

Целое десятичное число делится нацело на основание 2.

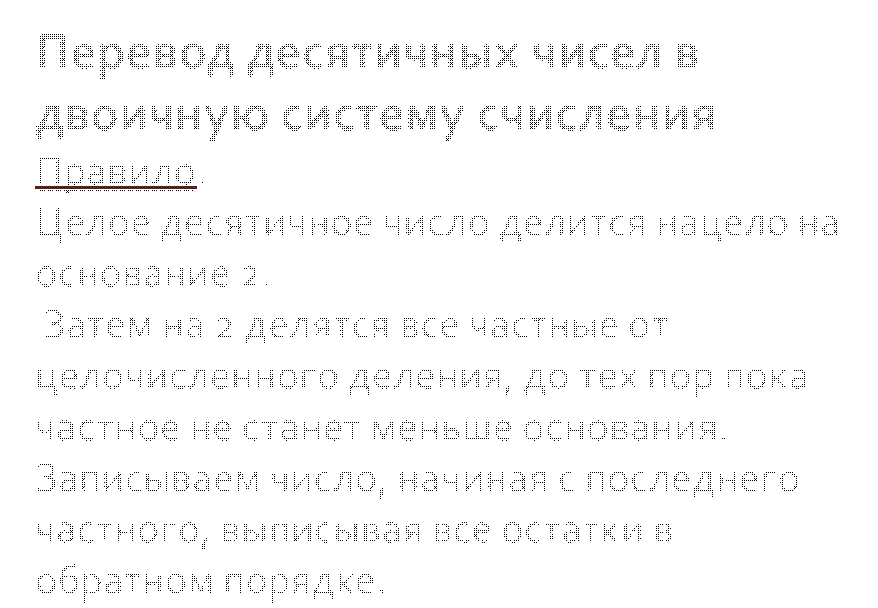Затем на 2 делятся все частные от целочисленного деления, до тех пор пока частное не станет меньше основания. Записываем число, начиная с последнего частного, выписывая все остатки в обратном порядке.

Примеры:

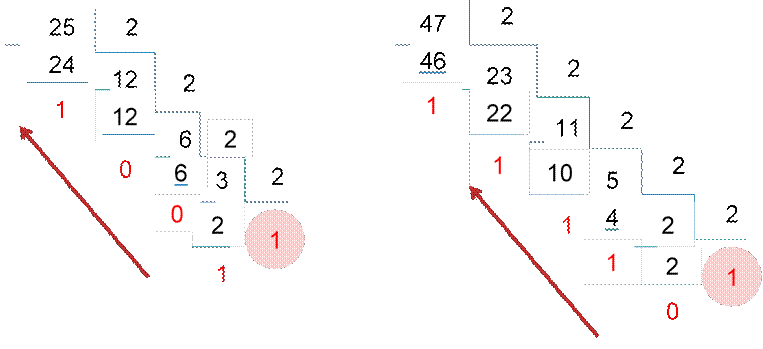
Задания на карточках

Перевести числа из десятичной системы счисления в двоичную:

                   27₁₀ = 11011₂                 23₁₀ = 10111₂

Задания на карточках

Перевести числа из десятичной системы в другие системы счисления:

Двоичная система счисления

Основание: 2

Алфавит: 0, 1

Вся информация в памяти компьютера представлена в двоичном коде

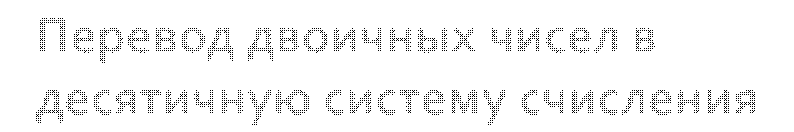Перевод двоичных чисел в десятичную систему счисления

Правило: данное двоичное число представить в развернутой форме, а затем найти сумму произведений. Примеры:

3  2  1   0

1 0 1 0₂ = 1*2³+0*2²+1*2¹+0*2⁰ = 8+ 2 = 10₁₀

6 5 4  3  2 1 0

1   0 1 0 1 1 1₂ = 1*2⁶+0*2⁵+1*2⁴+0*2³+1*2²+1*2¹+1*2⁰ = = 64+16+4+2+1 = ⁸⁷₁₀

Перевод чисел из других систем в десятичную систему счисления

2   1  0

2 0 2₃ = 2*3²+0*3¹+2*3⁰ = 18 + 2 = 20₁₀

4  3  2 1 0

1   0 2 0 1₃ = 1*3⁴+0*3³+2*3²+0*3¹+1*3⁰ =

= 81+18+1 =  ¹⁰⁰₁₀

2   1  0

2 1 0₅ = 2*52+1*51+0*50 = 50 + 5 = 55₁₀

2  1  0

1 1 4₈ = 1*8²+1*8¹+4*8⁰ = 64 + 8 + 4 = 76₁₀

Задания на карточках

Перевести данные числа в десятичную систему счисления:

Считаем палочки

10            1       2         3       4       5

с/с

                   2       1       10      11     100    101

с/с

Считаем палочки

10                1    2     3     4   5      6    7   8   9   10

с/с

5 1   2   3   4 10   11 12 13 14 20 с/с

Игра «Угадай соседей числа»

Игра «Угадай соседей числа»

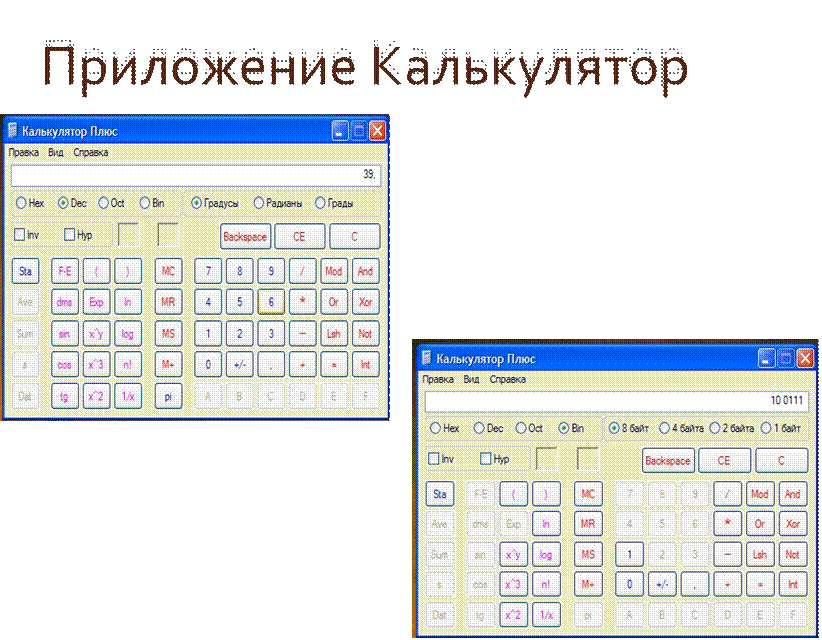
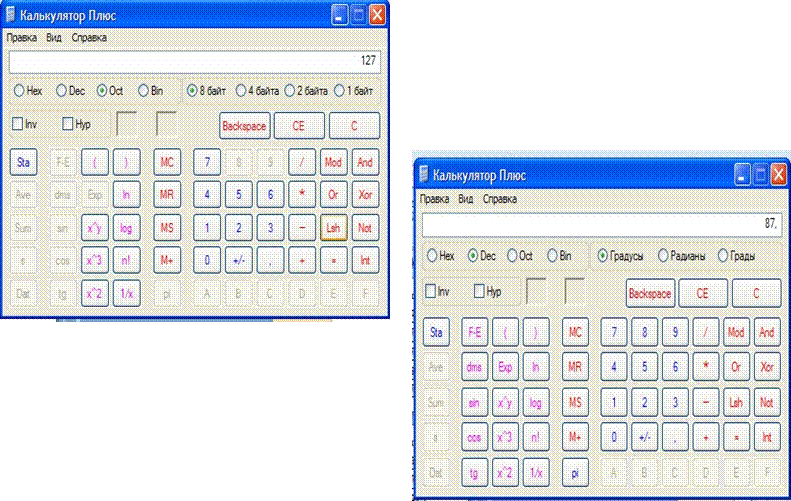
Приложение Калькулятор

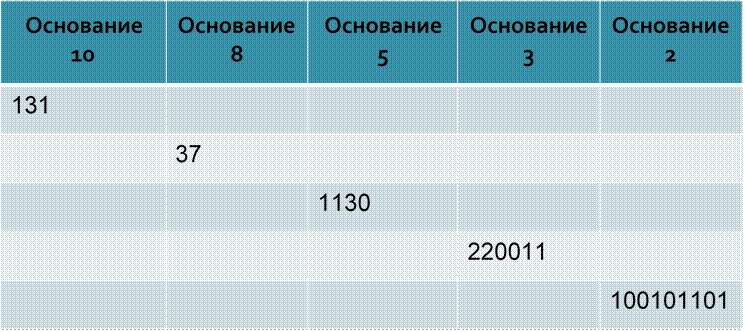
Домашнее задание

Заполнить таблицу