
Практическая работа 5 (6 ч.). Применение указанных методик подготовки обучающихся к государственной итоговой аттестации. Решение заданий ОГЭ и ЕГЭ по физике по трудным темам предметного содержания.
Цель: отработка методики решения заданий ОГЭ и ЕГЭ по физике по трудным темам предметного содержания.
Задание 1. Опишите фрагмент урока по подготовке учащихся к выполнению графических заданий.
Задание 2. Опишите фрагмент урока по подготовке учащихся к выполнению заданий логических, требующих как краткого, так и развернутого ответа.
Практическая работа должна быть выполнена на листах формата А4.
Оформление каждого нового структурного элемента работы начинается с новой страницы. Страницы практической работы должны быть пронумерованы.
Объем выполненной работы – не менее 2 страниц.
Критерии оценки:
- степень реализации цели практической работы;
- степень выполнения заданий работы;
- степень сформированности у слушателей необходимых знаний и умений;
Оценка: зачет/незачет.
Задание 1.
Этап изучения. Исследование свойств функции из определения конкретной тригонометрической функции в процессе решения типовых заданий физического содержания на формирование умений проводить теоретическое исследование.
Задание «Исторические сведения»
Цель: формирование умения оценивать факты, события, явления и процессы с помощью разных критериев, выделять причинно-следственные связи.
Возраст: 17 — 18 лет.
Учебные дисциплины: математика и физика.
Форма учебно-познавательной деятельности: работа индивидуальная и в группах по 4—5 человек.
Описание задания: учащимся предлагается провести теоретическое исследование. Теоретическое исследование – это формулирование общих закономерностей, позволяющих объяснить ранее открытые факты и эмпирические закономерности. Оно направлено на формирование таких умений структурировать и достраивать учебную информацию, которые способствуют её пониманию. Исследуя проблему, связанную с пониманием смысла новой информации, психологи установили, что о понимании текста свидетельствует способность преобразовывать изученный материал из одной формы в другую; интерпретировать изученный материал; предположить дальнейший ход развития действий, явлений и др. [29].
Этапы проведения исследования
1. Формулирование проблемы.
2. Подготовка к проведению исследования:
- предварительный анализ имеющейся информации, выдвижение гипотез;
- отбор материала, который будет использован в исследовании.
3. Проведение исследования:
- анализ и обобщение результатов исследования.
4. Изложение результатов исследования, их представление.
5. Обсуждение, оценка полученных результатов.
Материал: текст на карточке.
Текст. [6, с. 55]
На пороге XVII в., в развитии
тригонометрии намечается новое направление – аналитическое. Если до этого
главной целью тригонометрии считалось решение треугольников, вычисление
элементов геометрических фигур и учение о тригонометрических функциях строилось
на геометрической основе, то в XVII – XIX вв. тригонометрия
становится из глав математического анализа. Она находит широкое применение в
механике, физике и технике, особенно при изучении колебательных движений и
других периодических процессов. О свойстве периодичности тригонометрических
функций знал ещё Виет, первые математические исследования которого относились к
тригонометрии. Швейцарский математик Иоганн Бернулли (1642-1727) уже применял
символы тригонометрических функций. И если развитие алгебраической символики,
введение отрицательных чисел и направленных отрезков содействовали расширению
понятия угла и дуги, то развитие учения о колебательных движениях, о звуковых,
световых и электромагнитных волнах привело к тому, что основным содержанием
тригонометрии стало изучение и описание колебательных процессов. Из физики
известно, что уравнение гармонического колебания (например, колебания маятника,
переменного электрического тока) ![]() имеет вид
имеет вид
y = A sin (![]() t + α),
t + α),
где А – амплитуда отклонения маятника из положения равновесия,
![]() ‑ циклическая
частота, α - угол отклонения
от положения равновесия. Графиками гармонических колебаний являются синусоиды,
поэтому в физике и технике сами гармонические колебания часто называют
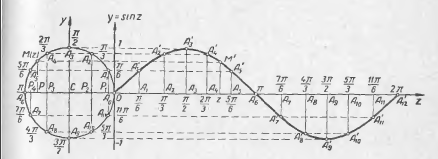
синусоидальными колебаниями (смотри рис.8).
‑ циклическая
частота, α - угол отклонения
от положения равновесия. Графиками гармонических колебаний являются синусоиды,
поэтому в физике и технике сами гармонические колебания часто называют
синусоидальными колебаниями (смотри рис.8).
 В первой половине XIX в. французский
учёный Ж. Фурье доказал, что всякое периодическое движение может быть
представлено (с любой степенью точности) в виде суммы простых гармонических
колебаний.
В первой половине XIX в. французский
учёный Ж. Фурье доказал, что всякое периодическое движение может быть
представлено (с любой степенью точности) в виде суммы простых гармонических
колебаний.
В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая её часть – учение о тригонометрических функциях – является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть – решение треугольников – рассматривается как глава геометрии (плоской и сферической).
Вопросы:
1. Назовите имена учёных, которые участвовали в создании тригонометрических функций. Что их к этому подвигло?
2. На рисунке 8 исследуйте синусоиду, для этого заполните сравнительную таблицу (см. табл. 13).
3. Подведите итоги наблюдений в виде таблицы результатов (см. табл. 14).
4. Постройте график функции у = sin z полностью путём параллельного переноса уже построенной части вдоль оси абсцисс на отрезки, кратные 2π.
5*. Что является графиком функции у = sin z?
6**. При каких значениях z на отрезке от 0
до 2π выражение ![]() имеет действительное значение?
имеет действительное значение?
Примечание: задание можно предложить решать при создании на уроке проблемной ситуации (на уроке – изучение нового материала, работая в парах по 2 человека, как и, при проведении обобщающего урока).
Ожидаемый результат.
Таблица 1. Сравнительный результат.
|
№ |
План сравнения |
на единичной окружности |
на графике |
|
1. |
Пока z возрастает от 0 до |
точка М(z) описывает первую четверть числовой окружности, а её ордината у = sin z возрастает от 0 до 1 |
график функции у = sin z плавно
поднимается вверх от оси Оz до прямой, параллельной оси Оz и отстоящей от неё на расстоянии R=1, следовательно, функция в промежутке [0; |
|
2. |
Дальше z возрастает от |
точка М(z) описывает вторую четверть числовой окружности, а её ордината у = sin z убывает от 1 до 0 |
График функции у = sin z опускается до
оси Оz, следовательно, функция в
промежутке [ |
|
3. |
С возрастанием z от π
до |
точка М(z) описывает третью четверть числовой окружности, а её ордината у = sin z убывает от 0 до - 1 |
График функции у = sin z продолжает
опускается ниже оси Оz до параллели к этой оси,
отстоящей от неё на расстоянии – 1, следовательно, функция в промежутке [π; |
|
4. |
Пока z возрастает от |
точка М(z) описывает последнюю четверть числовой окружности и возвращается снова в своё исходное положение, а её ордината у = sin z возрастает от - 1 до 0 |
График функции у = sin z снова
поднимается вверх до оси Оz и,
следовательно, функция в промежутке [ |
Таблица 2. Итог наблюдений.
|
Характер изменения |
I четверть |
II четверть |
III четверть |
VI четверть |
|
абсциссы z возрастает |
от 0 до
|
от |
от π до |
от |
|
функции у = sin z |
возрастает от 0 до 1 |
убывает от 1 до 0 |
убывает от 0 до – 1 |
возрастает от – 1 до 0 |
5*. Что является графиком функции у = sin z?
Графиком функции у = sin z является бесконечная непрерывная периодически волнообразная кривая, расположенная между двумя прямыми, параллельными оси абсцисс и отстоящими от неё на расстоянии равном 1; эту кривую называют синусоидой.
6**. При каких значениях z на отрезке от 0
до 2π выражение ![]() имеет действительное значение? (0
имеет действительное значение? (0 ![]() z
z ![]()
![]() π и
π и ![]() π
π ![]() z
z ![]() 2π).
2π).
Задание 2
Задания для освоения приёмов логического запоминания информации, извлечённой из текстов
Цель: освоение приёмов логического запоминания информации, извлечённой из текстов.
Возраст: 16-17 лет.
Учебные дисциплины: физика, математика.
Форма выполнения задания: работа индивидуальная, в парах и группах.
Описание задания: после чтения и составления плана текста и графических схем учащимся предлагаются следующие варианты выполнения задания:
- взаимная проверка по вопросам учебника с опорой на план текста;
- пересказ в парах с опорой на план и графическую схему;
 - составление
устной и письменной аннотации с опорой на план и графическую схему;
- составление
устной и письменной аннотации с опорой на план и графическую схему;
- подготовка учебных докладов с подбором иллюстративного материала.
Критерии оценивания:
· адекватность и точность воспроизведения текста;
· адекватность отражения и аннотации основных положений текста;
·
![]() адекватность
отражения в графической схеме логических и смысловых связей фрагментов текста.
адекватность
отражения в графической схеме логических и смысловых связей фрагментов текста.
Рассмотрим работу с текстом математического содержания на примере задания «Доказательство математических теорем с помощью физических понятий»
Текст [2, с.120]
Каждому приходилось наблюдать за движением различных частей всевозможных машин и станков.
Характерной особенностью часто встречающихся движений является их повторяемость через один и тот же промежуток времени. Такие движения называются периодическими.
Периодические процессы и явления изучаются физиками, механиками, астрономами, математиками и другими учёными. Закономерности тех или иных периодических явлений учёные записывают в виде функции, а затем, исследуя эти функции, раскрывают внутреннее содержание таких явлений и указывают пути практического использования на благо человека.
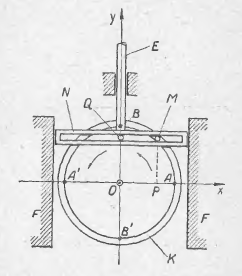
Рассмотрим более подробно из периодических процессов на примере простого механизма, в котором круговое движение преобразуется в прямолинейное (см. рис. 9).
Насаженное на ось О колесо К соединено посредством «пальца» М и рамкой N. При вращении колеса вокруг его оси палец М совершает круговое движение, увлекая за собой рамку, последняя скользит вдоль направляющих тисков F и совершает колебательное периодическое движение. Если рамку N соединить посредством штока Е с какой-нибудь деталью (например с поршнем насоса), то последняя будет совершать такое же движение, которое делает рамка.
Представим движение вращательного механизма, а именно: колесо вместе с пальцем М вращается равномерно вокруг оси с центром в точке О, а рамка, увлекаемая пальцем М, двигалась прямолинейно вверх и вниз, а вместе с ней прямолинейно двигался шток ВЕ. Рассмотрим две закономерности наблюдаемого движения:
I. Пусть колесо вращается равномерно с угловой скоростью ω = 1рад/с, тогда шток (любая его точка) будет двигаться прямолинейно неравномерно по закону: s = OQ = MP = y = sin t (см. рис.10):
а) вращение колеса равномерное;
б) шток движется прямолинейно неравномерно
– сначала замедленно, когда t изменяется от 0 до ![]() , а потом ускоренно, когда t изменяется от
, а потом ускоренно, когда t изменяется от ![]() до π.
до π.
II. Пусть шток движется прямолинейно равномерно со скоростью у = 1 рад/с, тогда обод колеса будет вращаться неравномерно по закону: s = МА = z = arcsin t (см. рис 11)
а) движение штока равномерное прямолинейное;
б) вращение обода неравномерное – сперва замедленное, когда t изменяется от – 1 до 0, а потом ускоренное, когда t изменяется от 0 до 1.
Доказать, что график функции y = sin t и обратной ей функции z = arcsin t (х = f(y)) симметричны относительно биссектрисы I и III координатной углов.


Материал: карточки со схемой организации деятельности при доказательстве теорем по Л.И. Боженковой [4].
Схема организации деятельности при доказательстве теорем.
1. Постановка учебной цели;
2) работа с формулировкой теоремы и выявление средств, необходимых для доказательства теоремы;
3) соотнесение выявленных средств выполнения УПД с собственными знаниями и умениями;
4) поиск доказательств теоремы;
5) составление плана доказательства теоремы;
6) реализация плана;
7) контроль доказательства теоремы;
8) самооценка результатов выполненной деятельности;
9) самокоррекция собственных учебных действий при работе с теоремой.
Ожидаемый результат:
1) доказать теорему обратимости функций и осознать приёмы, которые для этого использовались;
2) нужно знать приёмы обращения данной функции в обратную, признаки равенства и подобия треугольников, движение точки, выбрать подходящую формулу;
3) принять решение о помощи;
4) вывести следствия из равенства треугольников;
5) записать нужные отношения и преобразовать их, можно воспользоваться приёмами записи доказательства теоремы.
Задание на формирование ПУД и РУД. Организуйте свою учебную деятельность, направленную на доказательство того, что график любой обратной функции строится зеркальным отражением графика прямой функции относительно биссектрисы I – III координатных углов.
Таблица 15.
|
Первый уровень (базовый) |
Второй уровень (повышенный) |
Третий уровень (высокий) |
|
а) прочитайте доказательство теоремы; б) выполните пошаговую запись доказательства теоремы; составьте план, выполните обоснование каждого шага доказательства; в) попытайтесь сформулировать правило построения графиков обратных функций |
а) воспользуйтесь главной идеей, планом поиска доказательства и перечислите обоснования для каждого шага; б) запишите доказательство теоремы, используя приём и план; в) сравните обоснования, указанные в доказательстве текста, и в своей записи доказательства; г) сформулируйте правило построения графиков обратных функций |
а) используя главную идею доказательства, осуществите поиск, составьте план доказательства и запишите его; б) сравните доказательство с текстом со своим доказательством; в) сформулируйте правило построения графиков обратных функций, другие виды утверждений на примере задания и установите их истинность; г) подготовьте выступление с доказательством задачи у доски; д) примените правило к построению графиков обратных функций: линейной, квадратичной, логарифмической. |
Таким образом, диагностика, контроль и оценка метапредметных образовательных результатов, в которые включены познавательные УУД, проводятся на основании создаваемой учеником образовательной продукции – текстов, суждений, моделей, мета-алгоритмов, образов, исследований, проектов, выполненных тестов, выводов, полученных в результате наблюдения или эксперимента и т.п. Планировать создание такой продукции необходимо на этапе целеполагания как при постановки образовательной цели, так и метапредметной. Необходимым условием достижением этих результатов является выполнение учениками типовых учебных заданий, которые иллюстрируются на содержании курса математики и физики десятых и одиннадцатых классов.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.