Муниципальное  общеобразовательное учреждение

Средняя общеобразовательная школа № 3

 

 

 

 

 

 

 

 

Проект по математике

«Математическое вышивание»

 

 

 

Работу выполнили: Адам И.

Артемьева О.

Хадридинова С.

Руководитель: Ямщикова О.Б.

 

 

 

 

 

 

 

Магнитогорск

2021

СОДЕРЖАНИЕ

    ВВЕДЕНИЕ ...................................................................................................... 3

1   ЦЕЛИ И ЗАДАЧИ ............................................................................................. 4

2   ОСНОВНАЯ ЧАСТЬ ........................................................................................ 5

2.1   Понятие математического вышивания  ................................................... 5

2.2   Основные приемы математического вышивания ................................... 7

2.3   Замечательные кривые ............................................................................ 18

3   ЗАКЛЮЧЕНИЕ ............................................................................................... 19

     СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ................................... 20

       ПРИЛОЖЕНИЕ А ......................................................................................... 21        ПРИЛОЖЕНИЕ Б .......................................................................................... 22

       ПРИЛОЖЕНИЕ В ......................................................................................... 24

ВВЕДЕНИЕ

Процесс изучения математики – сложный и тернистый. Познавая новые ступени математики, мы получаем новые, ни на что не похожие слагаемые, которые помогают нам приблизиться к пониманию окружающего мира, к созданию красоты, единства и гармонии. 

Что же такое гармония? У этого слова много определений: связь, соединение, соответствие, соразмерность, единство частей – все это ничто иное, как гармония. 

Снаружи гармония может проявляться во многом – в мелодии, ритме, в музыке и живописи, симметрии и пропорциональности. Последние две характеристики относятся, прежде всего, к математике. Ведь математика – это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты. А красота многогранна и многолика. 

 

Актуальность

С первого класса  мы увлекаемся вышиванием. Сделанные свои руками вещи всегда ценятся в современном мире: ведь благодаря им наш дом становиться непохожим на другие, наполняется уютом и теплом. Декоративное панно, сувениры, закладки, карандашницы и различные композиции – все это можно сделать в технике вышивания «Изонить». Таким образом, на уроке геометрии у нас возник вопрос: какая связь между математическим вышиванием и геометрией?

 

 

 

 

 

 

 

 

1   ЦЕЛЬ 

Изучение  математических и геометрических законов, используемых при вышивание по окружности.

ЗАДАЧИ

1        Выделить основные математические понятия, используемые  в вышивании с помощью техники «Изонить»;

2        Найти зависимость рисунка от математической модели  исходного чертежа;

3        Сформировать практические навыки изображения геометрических фигур с помощью нитяной графики;

4        Развить творческую и познавательную активность, художественное восприятие и вкус;

5        Развить абстрактное мышление, обучиться плоскостному моделированию, умению составлять из геометрических фигур изображения предметов и композиций;

6        Показать возможность использования данного материала на уроках математики и ИЗО.

 

 

 

 

 

 

 

 

 

 

 

 

 

2   ОСНОВНАЯ ЧАСТЬ

2.1   Понятие математического вышивания

Паутины создаются в природе, их плетет паук, и они невероятно красивые. Кажется, что человек не способен создать такую красоту сам, но на самом деле, все далеко не так.. При помощи математического расчета можно сплести всевозможные кривые линии так, что получится любая, самая совершенная по своей красоте паутина. 

В XXI веке в женских школах был популярен преподавали такой предмет как «математическое вышивание».

Математическое вышивание – это метод конструирования кривых,  используя знакомые приемы построения геометрических фигур  (построение прямого угла с помощью угольника, деление отрезка на равные части, соединение точек в определенной последовательности, деление окружности на равные части с помощью циркуля и транспортира). Математическую вышивку можно выполнять на кусочке картона цветными нитками. Кроме своей привлекательности, решение задач способом математического вышивания позволяет расширить геометрические представления, развивает аккуратность, внимательность и трудолюбие. 

Метод «математическое вышивание» имеет удивительное сходство с давно известным видом декоративно-прикладного искусства – изонитью.

 Изонить или нитяная графика – это графическое изображение, особым способом выполненное нитками на твердом основании. Другое ее название – хордовая вышивка. Это оригинальный вид декоративно-прикладного искусства, уходящий корнями к народным мастерам Англии. Английские ткачи придумали особый способ переплетения нитей. Они вбивали в дощечки гвозди и в определенной последовательности натягивали на них цветные нити. В результате получались ажурные кружевные изделия, которые использовались для украшения жилищ, предметов быта, для оформления интерьера, для изготовления подарков и сувениров.

Достоинство изонити еще и в том, что выполняется она очень быстро и  аккуратно с первого раза, да и фантазии есть, где разгуляться.

Каждый стежок выверен и на своём месте.  В любом рисунке чувствуется присутствие математической точности, идеальности.  Изонить сродни калейдоскопу. Сочетая треугольники, окружности, прямые линии, овалы, ромбы, прямоугольники и т.д. можно получить  множество узоров и картин.  

Математическое вышивание – искусство или математика?

          Техника изонити – это чистая математика:

1        Геометрия: понятие об углах, величине, длине сторон, понятие об окружности, о середине, центре, хорде разной длины и её направлении;

2        Раздел «Количество и счёт»: упражнения в количественном и порядковом счёте. Закрепляется понятие о точке отсчёта и что результат количественного счёта не зависит от начала отсчёта и направления счёта; 

3        Раздел «Ориентировка на плоскости»: знание направлений: вверх, вниз, слева, справа; 

4        Раздел «Симметрия»;

5        Раздел «Замечательные кривые» – кардиоида, нефроида, астроида, улитка Паскаля, логарифмическая спираль и другие;

6        Изображение разных углов, окружностей, дуг, овалов, завитков, треугольников и других фигур и моделирование с их использованием образцов.

 

 

 

 

 

 

 

2.2   Основные приемы математического вышивания

В изонити всего три основных приёма: заполнение угла, заполнение окружности и заполнение дуги. Для этого необходимо вспомнить кое-что из математики.

Основные геометрические фигуры, используемые в вышивании изонить: окружность и угол.

1        Окружность – геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.

Отрезок, соединяющий центр с какой-либо точкой окружности называется радиусом.

Все радиусы окружности имеют одну и ту же длину.

Хорда – отрезок, соединяющий две точки окружности.

Диаметр – хорда, проходящая через центр окружности.

2        Угол – геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Чтобы вышить с помощью изонити, необходимо разделить окружность на равные части и провести хорды равной длины или на сторонах угла от его вершины отложить одинаковое количество равных отрезков и соединить их попарно в определенной последовательности: заполнение окружности и последующее разделение окружности на равные части с помощью транспортира.

 

 

 

 

 

 

 

1 Разобьем окружность  с центром в точке О на 4 равные части, каждая из которых будет равна 90⁰, как это представлено на рисунке 1. 

 

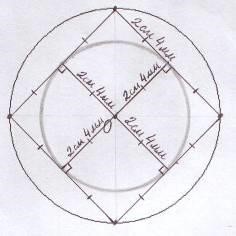
Рисунок 1 – Результат разбиения окружности 2 Проведем хорды, не совпадающие с диаметром. 

3                   Измерим расстояние от центра окружности до хорд. Для этого опустим перпендикуляры из центра к хордам. Они равны. Значит, основания перпендикуляров лежат на окружности с центром в точке О и радиусом, равном длине перпендикуляра. Основания перпендикуляров – середины хорд.                 

 

4                   Разделим окружность с центром в точке О на 5 равных частей, каждая из которых будет равна:

 

Проведем хорды, не совпадающие с диаметром. Возможно 2 случая: соединяем соседние точки или через одну. В обоих случаях образуется пятиугольник с равными сторонами, как можно увидеть на рисунке 2. 

 

 

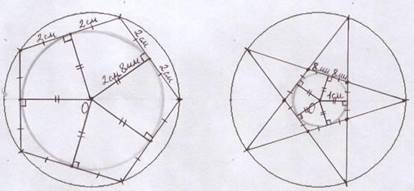
Рисунок 2 – Пятиугольники с равными сторонами

5                   Измерим расстояние от центра окружности до хорд. Для этого опустим перпендикуляры из центра к хордам. Они равны. Значит основания перпендикуляров лежат на окружности с центром в точке О и радиусом, равном длине перпендикуляра.

6                   Разделим окружность с центром в точке О на 6 равных частей, каждая из которых: 

 

Проведем хорды, не совпадающие с диаметром. Возможно 2 случая: соединяем соседние точки или через одну. В обоих случаях образуется шестиугольник с равными сторонами, представленный на рисунке 3.

 

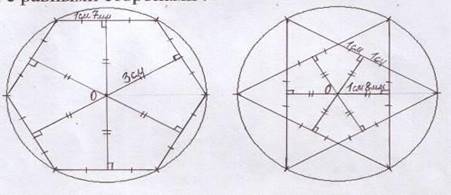
Рисунок 3 – Шестиугольники с равными сторонами

7                   Измерим расстояние от центра окружности до хорд. Для этого опустим перпендикуляры из центра к хордам. Они равны. Значит основания перпендикуляров лежат на окружности с центром в точке О и радиусом, равном длине перпендикуляра. 

Аналогично  поступаем при делении окружности на  8, 9, 10, 12, 18, 24 и  36 частей, что можно увидеть на рисунках 4 и 5.

 

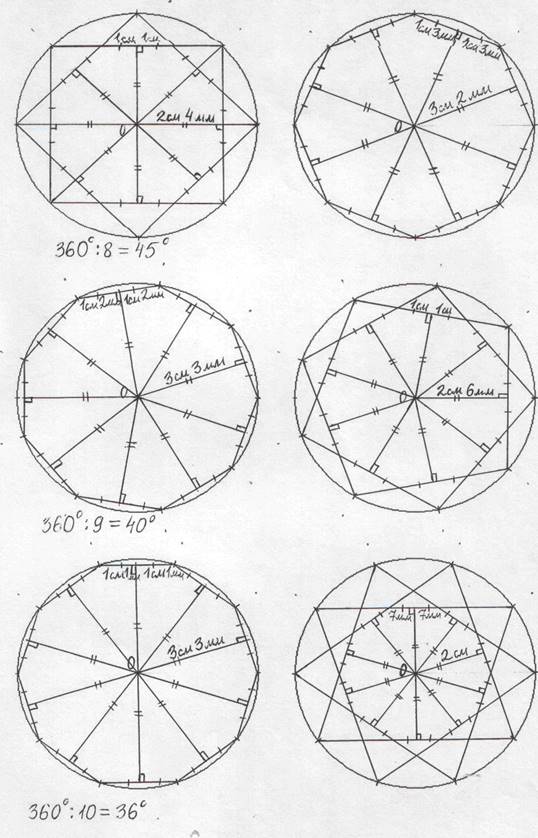
Рисунок 4 – Многоугольники

 

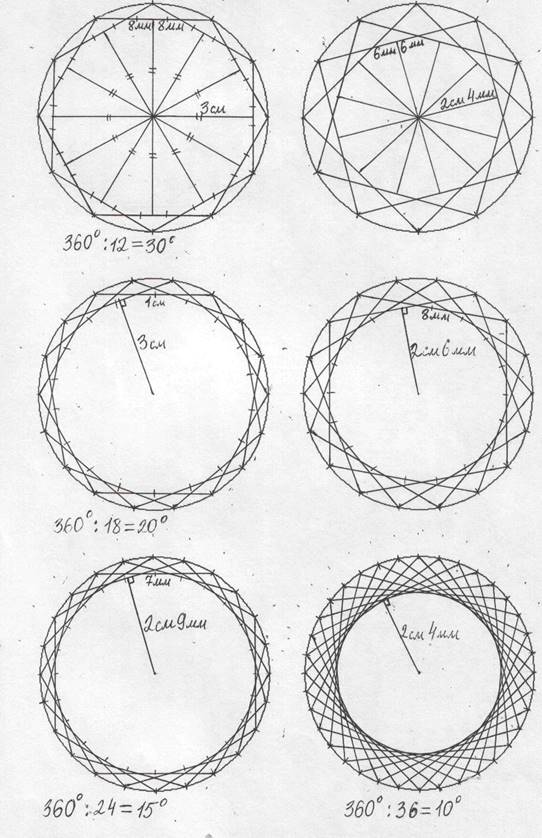
Рисунок 5 – Многоугольники

 

 

 

Заполнение окружности

1        Начертить окружность нужного размера на изнаночной стороне – рисунок 6;

2        Разделить окружность на равные части по всему периметру (можно разные). Число делений должно быть четное;

3        Размеченные точки проколоть иглой, пронумеровать – рисунок 7;

4        Пронумеруйте сначала точки с внешней стороны окружности;

5        Затем пронумеруйте внутри него. Внутреннюю нумерацию начинают с той точки, в которую хотят ввести иглу в первый раз. Внимание! Чем ближе точка, тем больше узор примыкает к окружности;

6        Затем, как  при заполнении угла соединяем точки, имеющие одинаковые номера – рисунок 8;

7        Внимание! При правильном заполнении на лицевой стороне рисунок напоминает звезду, каждой точке игла проходит два раза, а на изнанке

– повторяет линию окружности – рисунок 9;

8        Если кончается нить, то на изнаночной стороне закрепить нитку и продолжить работу.

 

Рисунок 6 – Первый шаг

 

Рисунок 7 – Третий шаг

 

Рисунок 8 – Шестой шаг

 

Рисунок 9 – Седьмой шаг

          Технология выполнения рисунков одинакова, но результат разный, так как разный шаг (количество пропущенных точек). Нами выявлено, что шаг должен делиться на 3.

Если окружность разделить на равные части и провести все хорды равной длины, то они от центра окружности находятся на одинаковом расстоянии. Середины хорд лежат на окружности с тем же центром, что и исходная окружность. Чем длиннее хорда, тем меньше получится центральное отверстие. Изменяя длину хорды и количество точек, на окружностях с равным диаметром можно получить разнообразные узоры. 

Заполнение угла

1        Начертить угол нужного размера на изнаночной стороне основы;

2        Разделить стороны угла на равные части и пронумеровать их (вершина угла пропускается). Число точек деления на одной и другой стороне угла должно быть одинаково, а расстояние между точками деления на сторонах угла может быть и разная;

3        Внимание!  Нумерация точек на одной стороне угла начинается от вершины к краю, на другой – от края к вершине;

4        Проколоть намеченные точки иглой;

5        В точке 1 с изнанки закрепить нитку скотчем, затем сделать стежок 1 – 1, далее маленький стежок с изнанки 1 – 2, стежок по лицевой стороне 2 – 2, по изнанки 2 -3, по лицевой стороне 3 – 3 и т. д.;

6        Если кончается нить, то на изнаночной стороне закрепить нитку и продолжить работу;

7        В каждой точке игла проходит один раз;

8        Внимание! На изнаночной стороне располагаются короткие стежки между соседними точками вдоль стороны угла, а по лицевой стороне - длинные стежки между точками с одинаковыми номерами на разных сторонах угла. Если это так, то работа выполнена правильно;  

9        Чем меньше шаг разметки, тем плотнее и чаще заполняется угол, а чем больше шаг, тем прозрачнее заполнение угла.

Наглядную схему заполнения угла можно увидеть на рисунках 10 и 11. 

На рисунках 12, 13 показаны заполненные углы.

 

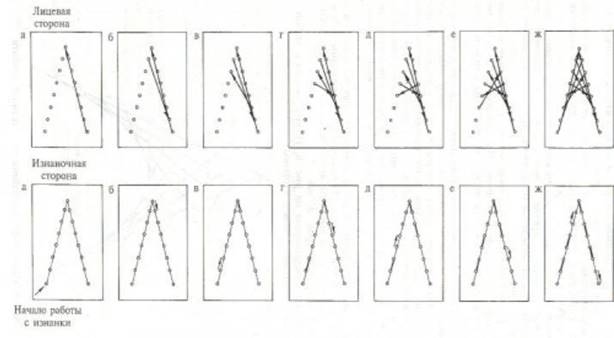
Рисунок 10 – Заполнение угла

 

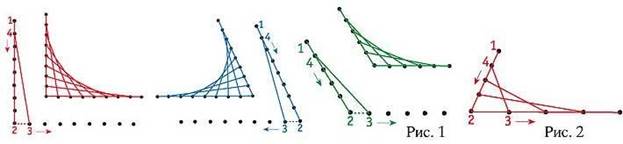
Рисунок 11 – Заполнение угла

 

Рисунок 12 – Заполненный угол

 

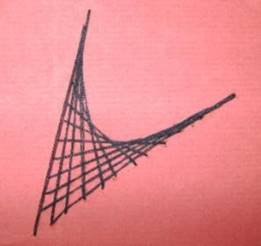
Рисунок 13 – Заполненный угол Заполнение дуги

1        Необходимо начертить дугу, разделив ее на равные части;

2        Сделать проколы в точках деления;

3        Вдеть нитку в уголку и заполнить фигуру по схеме.

Эффектнее выглядит дуга, у которой больше искривление и чаще расположены точки. 

Схема заполнения дуги представлена на рисунке 14. 

Визуально можно увидеть заполненные дуги на рисунках 15 и 16.

 

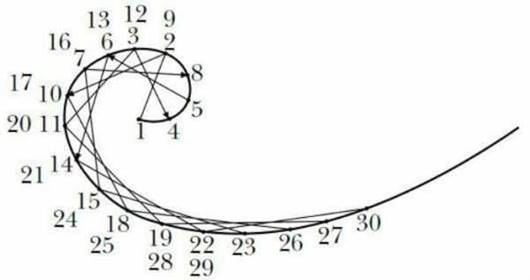
Рисунок 14 – Схема заполнения дуги

 

 

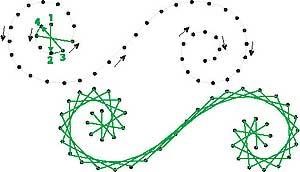
Рисунок 15 – Заполненная дуга

 

Рисунок 16 – Заполненная дуга

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.3   Замечательные кривые 

В разговорном языке слова «кривой», «кривая», «кривое» употребляются как прилагательные, обозначающие то, что отклоняется от прямого, от правильного, от справедливого. Говорят о кривой палке, о кривой дороге, о кривом зеркале; «богат, да крив; беден, да прям», – гласит пословица.

Математики употребляют слово «кривая» обычно в смысле существительного; они разумеют под этим словом кривую линию. Что же такое кривая линия? Как охватить в одном определении все кривые, которые рисуются на бумаге карандашом или пером, на доске мелом, вычерчиваются на ночном небе «падающей звездой» или ракетой?

Кривая или линия — геометрическое понятие, определяемое в разных разделах геометрии различно.

1 Гипоцикло ида — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения. 2 Гипотрохоида — плоская кривая, образуемая фиксированной точкой, находящейся на фиксированной радиальной прямой окружности, катящейся по внутренней стороне другой окружности.

3                   Астроида — плоская кривая, описываемая точкой M окружности радиуса r, катящейся по внутренней стороне окружности радиуса R = 4r.

4                   Кардиоида — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.

 

 

 

 

 

 

3   ЗАКЛЮЧЕНИЕ

Тема «математическое вышивание» нам понравилась сразу! В результате ее изучения мы поняли универсальность математических знаний и законов в окружающем нас мире. 

Изучение темы «математическое вышивание» позволило нам расширить геометрические представления. Мы получили большое удовлетворение от процесса вышивания геометрических кривых и как следствие – результатов нашей работы. 

           Вышивка в стиле «изонить» очень увлекательное занятие. С её помощью можно выполнять различные композиции и панно, которые, несомненно, станут украшением, как дома, так и школьных кабинетов.

На наш взгляд, результаты данной работы можно использовать: на уроках математики в 5 классе при изучении темы «окружность», на уроках геометрии в 7-8 классах и на уроках технологии и ИЗО.

Жизнь настоятельно требует сегодня сделать эстетику не гостьей на уроке, а эффективным средством повышения качества воспитания и преподавания. Может, таким образом ученик и превратится из сосуда, который нужно наполнить, в факел, который нужно зажечь.

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1        Гусарова Н.Н. Техника Изонити для дошкольников. Методическое пособие. – СПб., «Детство-Пресс», 2000г.;

2        Леонова О.В. Рисуем нитью: Ажурные картинки. – М., «Литера»,

2005г.;

3        Сашко Л. Н. Хордовый стежок – Златоуст,  2004г.;

4        Мастер-класс по теме «Изонить» // – [Электронный ресурс]. URL: http://nauka.relis.ru/50/0412/50412116.html

5        Изонить     //       –        [Электронный     ресурс].      URL: http://kvazu.narod.ru/izonit.html

6        Технология         изонити      »        //        –        [Электронный     ресурс].      URL: http://uglichkukla.narod.ru/Teh_Izonit.htm

7        Математическое вышивание // – [Электронный ресурс].     URL: https://netrefs.ru/matematicheskoe-vishivanie.html

8        Нитяная графика // – [Электронный ресурс]. URL: http://nityanayagrafika.narod.ru/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ А

 

Этапы заполнения окружности  

 

 

 

 

 

ПРИЛОЖЕНИЕ Б

Примеры узоров

 

 

ПРИЛОЖЕНИЕ В

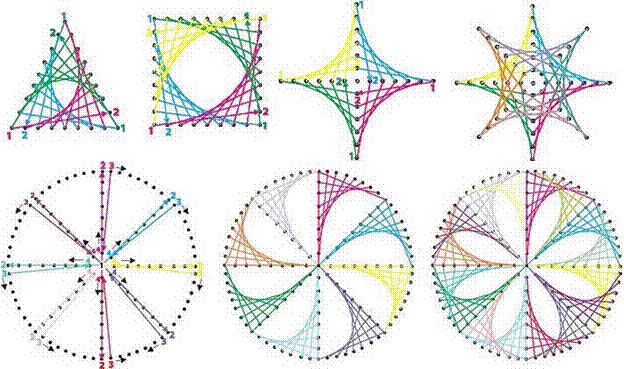
Наши работы