Проверочная работа по теме "Призма". Геометрия 11 класс.

Проверочная работа №1 « Призма».

(Ответить на вопросы. Заполнить пропуски. Решить задачи).

1.    Многогранник, составленный из двух равных многоугольников, лежащих в параллельных плоскостях, и нескольких параллелограммов, называется … .

2.    Сделать рисунок произвольной, например, пятиугольной  наклонной призмы и обозначить все ее вершины.

3.    Перечислить ее основания … 

4.    Основания любой призмы …  многоугольники.

5.    Перечислить ее боковые ребра …  .

6.    Перечислить ее боковые грани …  .

7.    Боковые грани являются …  .

8.    Боковые ребра любой призмы … по величине и … .

9.    Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется … призмы.

  10.По отношению боковых ребер к плоскости основания  

     призмы бывают … или … .

11.Если боковые ребра не перпендикулярны к плоскости основания, то призмы называют …  .

12. Если боковые ребра  перпендикулярны к плоскости основания, то призмы называют …  .

13. Высота прямой призмы равна ее …  …  .

14. Прямая призма называет правильной, если ее основания -  … многоугольники.

15.  Боковые грани правильной призмы являются … …  .

16. Боковая поверхность призмы складывается из суммы … ее … … .

17. S_бок. =…

18. Полная поверхность призмы складывается из суммы … всех ее … .

19.   S_{пр. = …}

20. Объем призмы равен произведению  площади … на ее ….

21.    V= … 

Решите задачи.

Задача 1. Основание прямой треугольной призмы – прямоугольный треугольник  с катетом 8 и гипотенузой 10. Боковое ребро призмы  равно 18. Вычислить объем призмы.

Задача 2. Через среднюю линию основания треугольной призмы , объем которой равен 124, проведена плоскость, параллельно боковому ребру. Найти объем оставшейся части после удаления отсеченной малой треугольной призмы.

Задача 3.  Вычислить площадь поверхности и объем.

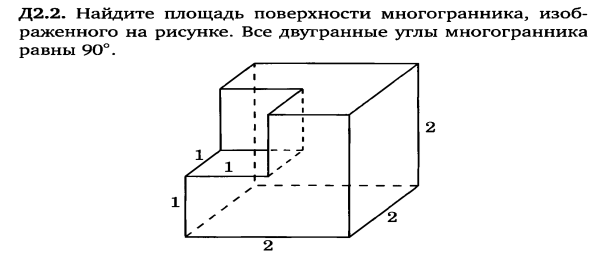
Задача 4. Вычислить площадь поверхности и объем.

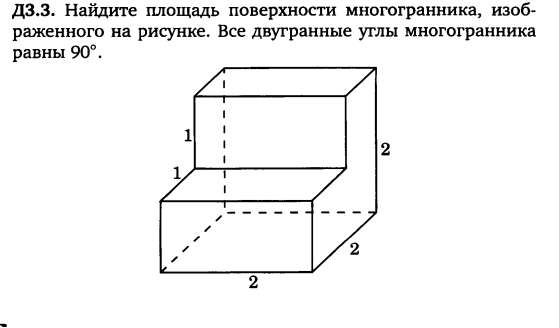
Задача 5.  Найти объем  и поверхность многогранника, вершинами  которого  являются вершины D, A₁, D₁, C₁, B₁, C  параллелепипеда ABCDA₁B₁C₁D₁, у которого  BA=8, BC=12, BB₁=5.

Задача 6.

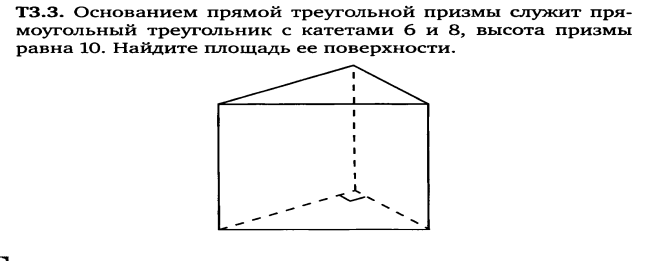Задача 7, 8.

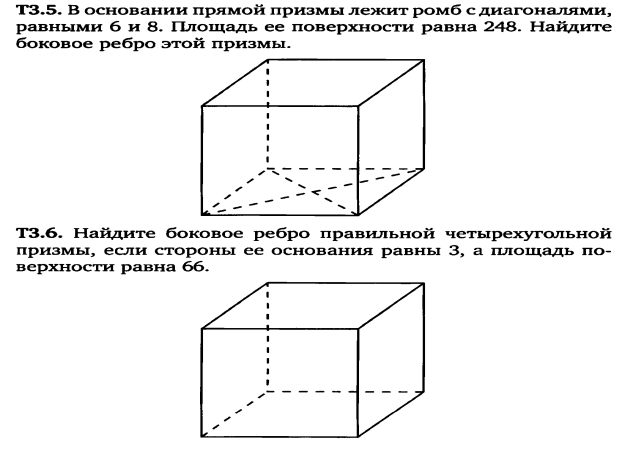
Задачи 9,10,11.