ПР_Задачи оптимизации (поиск решения) в MS Excel

Практическая работа №11

Тема: Задачи оптимизации (поиск решения) в MS Excel.

Цель: - изучение технологии поиска решения для задач оптимизации (минимизации, максимизации).

Вид работы: фронтальный

Время выполнения: 2 часа

Задания к практической работе

Задание 1. Минимизация фонда заработной платы фирмы.

Пусть известно, что для нормальной работы фирмы требуется 5…7 курьеров, 8…10 младших менеджеров, 10 менеджеров, 3 заведующих отделами, главный бухгалтер, программист, системный аналитик, генеральный директор фирмы.

Общий месячный фонд зарплаты должен быть минимален. Необходимо определить, какими должны быть оклады сотрудников фирмы, при условии, что оклад курьера не должен быть меньше 1400 р.

В качестве модели решения этой задачи возьмем линейную модель. Тогда условие задачи имеет вид N₁*A₁*x+N₂*(A₂*x+B₂)+...+N₈*(A₈*x+B₈) = Минимум, где N_i – количество работников данной специальности; x – зарплата курьера; A_i и B_i – коэффициенты заработной платы сотрудников фирмы.

Ход работы

1.   Запустите редактор электронных таблиц Microsoft Excel и откройте созданный в Практической работе 4 файл «Штатное расписание».

Скопируйте содержимое листа «Штатное расписание 1» на новый лист и присвойте копии листа имя «Штатное расписание 2».

2.   В меню Данные – Анализ «что – если» активизируйте команду Поиск решения (рис. 1).

3.   В окне Установить целевую ячейку укажите ячейку F14, содержащую модель – суммарный фонд заработной платы.

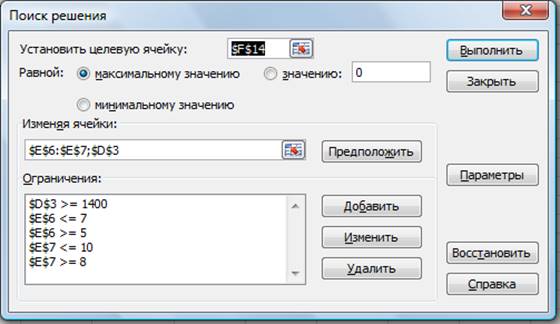
Рисунок 1 - Задание условий для минимизации фонда заработной платы

Поскольку необходимо минимизировать общий месячный фонд зарплаты, активизируйте кнопку равный – Минимальному значению.

В окне Изменяя ячейки укажите адреса ячеек, в которых будет отражено количество курьеров и младших менеджеров, а также зарплата курьера - $E$6:$E$7:$D$3 (при задании ячеек E6, E7 и D3 держите нажатой клавишу [Ctrl]).

Используя кнопку Добавить в окнах Поиск решения и Добавление ограничений, опишите все ограничения задачи: количество курьеров изменяется от 5 до 7, младших менеджеров од 8 до 10, а зарплата курьера >1400 (рис.2).

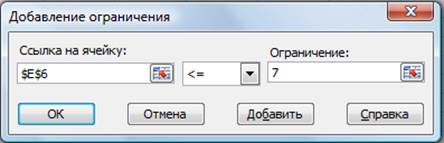
Рисунок 2 - Добавление ограничений для минимизации фонда заработной платы

Ограничения наберите в виде

$D$3>=1400

$E$6>5

$E$6<7

$E$7>=8

$E$7 <=10.

Активизируйте кнопку Параметры, введите параметры поиска, как показано на рис. 3.

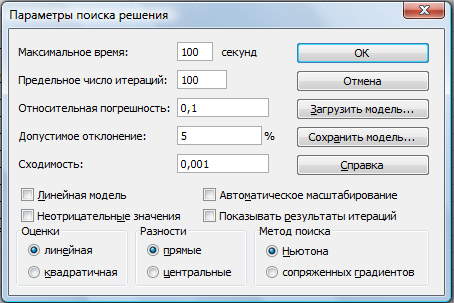
Рисунок 3 - Задание параметров поиска решения по минимизации фонда заработной платы.

Окончательный вид окна Поиск решения приведен на рис. 1.

Запустите процесс поиска решения нажатием кнопки Выполнить. В открывшемся диалоговом окне Результаты поиска решения задайте опцию Сохранить найденное решение (рис. 4).

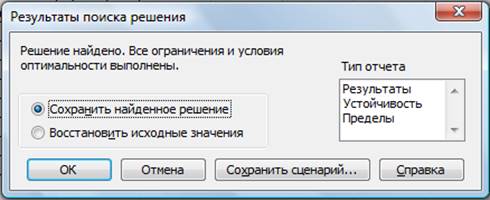
Рисунок 4 - Сохранение найденного при поиске решения

Решение задачи приведено на рис. 5. Оно тривиально: чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд заработной платы.

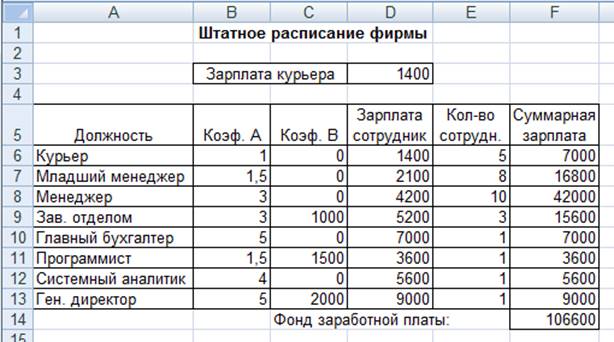
Рисунок 5 - Минимизация фонда заработной платы

Задание 2. Составление плана выгодного производства.

Фирма производит несколько видов продукции из одного и того же сырья – А, В и С. Реализация продукции А дает прибыль 10 р., В – 15 р. и С – 20 р. на единицу изделия.

Продукцию можно производить в любых количествах, поскольку известно, что сбыт обеспечен, но ограничены запасы сырья. Необходимо определить, какой продукции и сколько надо произвести, чтобы общая прибыль от реализации была максимальной.

Нормы расхода сырья на производство продукции каждого вида приведены в табл. 1.

Таблица 1

Ход работы

1.   Запустите редактор электронных таблиц Microsoft Excel и создайте новую электронную книгу.

2.   Создайте расчетную таблицу как на рис. 6. Введите исходные данные и формулы в электронную таблицу. Расчетные формулы имеют такой вид:

Расход сырья 1=(количество сырья 1) * (норма расхода сырья А) + (количество сырья 1) * (норма расхода сырья В) + (количество сырья 1) * (норма расхода сырья С).

Значит, в ячейку F5 нужно ввести формулу = B5*$B$9+C5*$C$9+D5*$D$9.

Обратите внимание, что значения количества сырья каждого вида пока не известны и будут подобраны в процессе решения задания (ячейки В9:D9 пока пустые).

(Общая прибыль по А) = (прибыль на ед. изделий А) * (количество А),

Следовательно в ячейку В10 следует ввести формулу = В8 * В9.

Итоговая общая прибыль = (Общая прибыль по А) + (Общая прибыль по В) + (Общая прибыль по С),

значит в ячейку Е10 следует ввести формулу = СУММ(В10:D10).

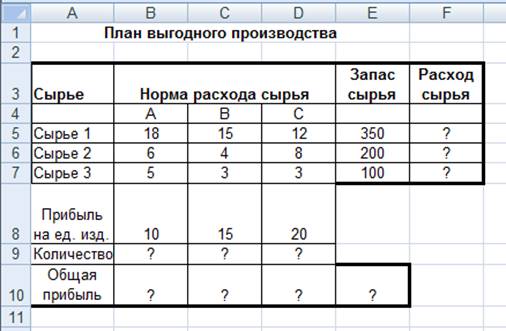
Рисунок 6 - Исходные данные для Задания 2

3.   В меню Данные активизируйте команду Поиск решения и введите параметры поиска, как указано на рис 7.

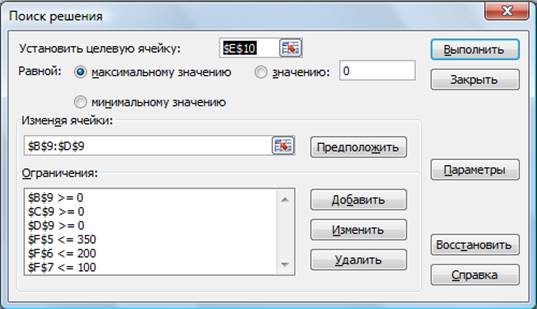
Рисунок 7 - Задание условий и ограничений для поиска решений

В качестве целевой ячейки укажите ячейку «Итоговая общая прибыль» (Е10), в качестве изменяемых ячеек – ячейки количества сырья – (В9:D9).

Не забудьте задать максимальное значение суммарной прибыли и указать ограничения на запас сырья:

расход сырья 1<=350; расход сырья 2<=200; расход сырья 3<=100, а также положительные значения количества сырья А,  В, С >=0.

Установите параметры поиска решения (рис. 8). Для этого кнопкой Параметры откройте диалоговое окно Параметры поиска решения, установите параметры по образцу, задайте линейную модель расчета (Линейность модели).

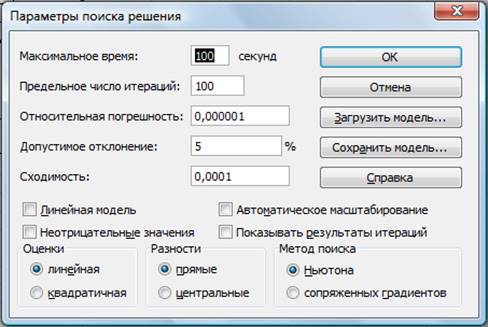
Рисунок 8 - Задание параметров поиска решения

4.   Кнопкой Выполнить запустите Поиск решения. Если вы сделали все верно, то решение будет как на рис. 9.

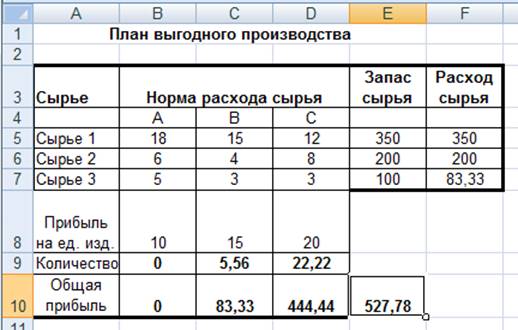
Рисунок 9 - Найденное решение максимизации прибыли при заданных ограничениях

5.   Сохраните созданный документ под именем «План производства».

Вывод. Из решения видно, что оптимальный план выпуска предусматривает изготовление 5,56 кг продукции В и 22,22 кг продукции С. Продукцию А производить не стоит. Полученная прибыль при этом состоит 527,78 р.

Задание 3. Используя файл «План производства» (см.задание 2), определить план выгодного производства, т. е. какой продукции и сколько необходимо произвести, чтобы общая прибыль от реализации была максимальной.

Выберите нормы расхода сырья на производство продукции каждого вида и ограничения по запасам сырья из таблицы соответствующего варианта (5 вариантов):

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Рекомендуемая литература: 1, 2, 3, 4