3-Маvzu: Gauss usuli bilan normal tenglashtirish sistemasida yechish  Reja.

Parametrik usulda tenglashtirish bajarish ketma-ketligi

I.            Barcha o‘lchashlar n, kerakli o‘lchashlar k va ortiqcha o‘lchashlar r soninini aniqlash.

II.        Soni kerakli o‘lchashlar k ga teng va bir-biri bilan bog‘liq bo‘lmagan, ya’ni har qanday parameter boshqasi orqali ifodalanmaydigan shartlarni qanoatlantirgan holda T₁,...,T_k parametrlarni tanlash. Bunda T_i  f_i (T₁,T₂,...,T_j1,T_j1,...,T_k ) funksiya sodir bo‘lmasligi kerak.

III.     X_i  f_i (T₁,...,T_k )     (i 1,2...,n)-parametrik tenglamalar bog’liqligini tuzish.

x_i v_i  f_i (t₁,....,t_k )

IV.     Tuzatmalarning parametrik tenglamasini tuzish

v_i  a_i1₁ a_i2₂ ....a_ik_k l_i (i 1,...,n)

yoki, matritsa ko‘rinishida

V  AX  L 

V.         Tuzatmalar normal tenglamalarini tuzish

                                   pa₁a₁₁ pa₁a₂₂ ....pa₁a_k _k pa₁l 0 

                                    pa₁a₂₁ pa₂a₂₂ ....pa₂a_k _k pa₂l 0         ^

.....................................................................................^_^.

                                    pa₁a_k ₁ pa₂a_k ₂ ....pa_ka_k _k pa_kl 0         _

yoki, matritsa ko‘rinishida

RX  A^TL  0 

bu yerda,  R_A^T _A-normal tenglamalar koeffisiyentlar matritsasi.

VI.     Tuzatmalarning normal tenglamalar sistemasini yechish. Bunga masalani matematikadagi nomalumlarni ketma-ket yo‘qotishga asoslangan: Xoletskiy, kvadrat ildizlar, Jordan, Gauss, Kramer va boshqa yechish usullaridan foydalanish mumkin. Masalan, Gaussda 3 noma’lumli 3 chiziqli aniqlangan tenglamalar sistemasini yechimidan kerakli noma’lumlarning taxminiy qiymatiga τ_v tuzatma olinadi: 

a₁a₁₁ a₁a₂₂ a₁a₃₃ a₁l 0 

a₁a₂₁ a₂a₂₂ a₂a₃₃ a₂l 0^.  

a₁a₃₁ a₂a₃₂ a₃a₃₃ a₃l 0^_

a₁a₁₁ a₁a₂₂ a₁a₃₃ a₁l 0 

................a₂a₂₂ a₂a₃₃ a₂l 0^_

.................................a₃a₃₃ a₃l 0^_

a³l *2

₃ 

a₃a₃ *2

                                                                                    a2a3 *1    a2l *1

                                                                        2                 3 

                                                                                    a₂a₂ *1   a₂a₂ *1

                                                                               a1a2   a1a3    a1l

                                                                   1            2           3 

                                                                               a₁a₁   a₁a₁   a₁a₁

 Uning matritsa ko‘rinishi

X R^1 A^TL  0

VII.   O‘lchash natijalariga tuzatmalar hisoblash

v_i  a_i1₁ a_i2₂ ....a_ik_k l_i (i 1,...,n)

yoki, matritsa ko‘rinishida

V  AX  L

VIII.    O‘lchangan kattaliklarning       x_i^’=x_i+v_i  va parametrlarning t_v=t_v⁰+τ_v  tenglashtirilgan qiymatlari topiladi.

IX.       Tenglashtirishni yakuniy tekshirish. Parametric tenglamalar bog‘liqligi x_i v_i  f_i (t₁,....,t_k ) da, tenglikining chap tomoniga o‘lchangan kattaliklarning

x_i^’=x_i+v_i  tenglashtirilgan qiymatlarini, o‘ng tomoniga esa parametrlarning t_v=t_v⁰+τ_v  tenglashtirilgan qiymatlarini qo‘yish kerak. Agar barcha tenglamalar bog‘liqligi uchun, chap tomon o‘ng tomonga teng bo‘lsa tizim tenglashtirilgan hisoblanadi.

X.          Aniqlikni baholash.

 

Parametrik usulda teng aniqlikdagi o’lchashlar natijasini tenglashtirish misoli.

 

1.1-masala. 1-rasmda burchaklarni o‘lchashni barcha kombinatsiyalar sxemasi va 1-jadvalda o‘lchash natijalari berilgan. Burchaklarni parametrik usul bilan tenglashtirish va aniqlikni baholash bajarish talab qilingan.  

1-jadval

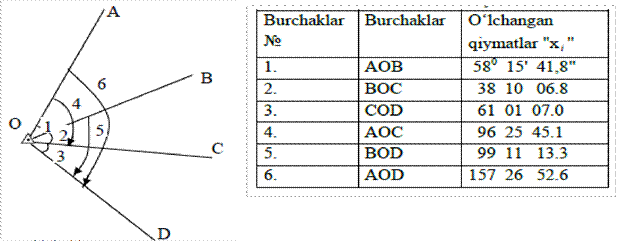
                1-chizma

 

Yechish.

I.            Kerakli va ortiqcha o‘lchashlar soninini hisoblaymiz. Barcha o‘lchashlar n=6, kerakli o‘lchashlar k=3 va ortiqcha o‘lchashlar r=n-k=6-3=3 ga teng bo‘ladi.

II.        Soni kerakli o‘lchashlar k=3 ga teng va bir-biri bilan bog‘liq bo‘lmagan, ya’ni har qanday parameter boshqasi orqali ifodalanmaydigan shartlarni qanoatlantirgan holda parametrlarni tanlaymiz. Bunda T_i  f_i (T₁,T₂,...,T_j1,T_j1,...,T_k ) funksiya sodir bo‘lmasligi kerak. Bu shartlarni boshlang‘ich uchta burchak qanoatlantiradi. Va ularni parametrlar sifatida qabul qilamiz T₁  X₁ :T₂  X₂;T₃  X₃. Ularning tenglashtirilgan qiymati sifatida t₁,t₂ va t₃ larni olamiz.

III.     X_i  f_i (T₁,...,T_k )     (i 1,2...,n)-parametrik tenglamalar bog’liqligini tuzish.

Hamma oltita o’lchangan miqdorlar tenglashtirilgan qiymatini uchta kerakli noma’lumlarning tenglashtirilgan qiymati orqali ifodalaymiz:

x_i  x₁ v_i  f_i (t₁,t₂,t₃)

Ko’rilayotgan misolimiz uchun tenglamalar bog’liqligi

1)    x₁  t₁                              4) x₄  t₁ t₂

2)    x₂  t₂                              5) x₅  t₂ t₃

3)    x₃  t₃                               6) x₆  t₁ t₂ t₃

III¹. Parametrlarning taxminiy qiymatlarini hisoblash. Ma’lumki parametrlar birinchi uchta o‘lchash natijalariga teng, parametrlarning taxminiy qiymatlari

sifatida        burchaklarning      o‘lchash      natijalarini   olamiz,   t₁  t₁⁰ ₁;..........;t_k  t_k⁰ _n   ga asosan yozamiz

                                            t1  t10 1;           t2  t20 2;              t3  t30 3.

bu yerda, t₁⁰  x₁  58⁰1541,8;  t₂⁰  x₂  38⁰1006,8; t₃⁰  x₃  61⁰0107,0.

 

IV. Tuzatmalarning parametrik tenglamasini tuzish.

 Umumiy holda x  x_i  v_i va v_i  a_i1₁  a_i2₂ ....... a_ik_k l_i larga asosan biz ko’rayotgan masala uchun tuzatmalarning parametric tenglamasi quyidagicha bo’ladi:

v_i  a_i1₁ a_i2₂ a_i3₃ l_i     i 1,2,....,6

bu yerda:

 xt i  ;      ai2   xt2i 0;     ai3   xt3i 0   ai1    1 0 

li  fi (t10,t20,t30)  xi  xi0  xi

Tuzatmalarning parametric tenglamasi kooeffisentlarini va ozod xadlarini har bir  tenglamalar bog’liqligi uchun yozamiz.

1-chi tenglamalar bog’liqligi uchun:

                                                      x                             

a11  t11 0 1;      a12 tx21 0 0;     a13 tx31 0 0



l₁  t_i⁰  x_i  x_i⁰  x_i  58⁰15^/41.8^// 58⁰15^/41.8^//  0

2-chi tenglamalar bog’liqligi uchun:

x

a21  t2  0 ;      a22 xt22 0 1;     a23 xt32 0 0

                                                       1 0                                             

l₂  x_i⁰  x_i  38⁰10^/06.8^// 38⁰10^/06.8^//  0

3-chi tenglamalar bog’liqligi uchun:

x3  0;      a32 tx23 0  0 ;     a33 xt33 0 1 a31  t1 0                 

l₃  x_i⁰  x_i  61⁰01^/07.0^// 61⁰01^/07.0^//  0

4-chi tenglamalar bog’liqligi uchun:

a41 xt14 0 1;      a42 xt24 0 1;     a43 xt34 0 0

l₄  x_i⁰  x_i  (t₁⁰ t₂⁰)  x₄  (58⁰15^/41.8^// 38⁰10^/06.8^// ) 96⁰25^/45.1^//  3.5^// 5-chi tenglamalar bog’liqligi uchun:

x5  0;      a52 xt25 0 1;     a53 xt35 0  0

                                   a51  t1 0                                         



l₅  (t₂⁰ t₃⁰)  x₅  (38⁰10^/06.8^//  61⁰01^/07.0^// ) 99⁰11^/13.3^//  0.5^// 6-chi tenglamalar bog’liqligi uchun:

a61 xt16 0 1;      a62 xt26 0 1;     a63 xt36 0 1 

l₆  (t₁⁰ t₂⁰ t₃⁰ )  x₆  (58⁰15^/41.8^//  38⁰10^/06.8^//  61⁰01^/07.0^// ) 

                                ⁰26^/52.6^// 3.0^//.                                                                     

157

Tuzatmalar tenglamalari koeffisiyentlari matrisasi quyidagi ko‘rinishda bo‘ladi 1.0.0 

                                                                                                            

0.1.0

^0.0.1^

                                                                                            A         

1.1.0 

^0.1.1^

                                                                                                            

1.1.1 

Hamma o’lchashlar uchun tuzatmalar tenglamasini yozamiz:

1). v₁  a₁₁₁ a₁₂₂ a₁₃₃ l₁ 1*₁ 0*₂ 0₃ 0 ₁ ga kora

v₁ ₁  bo’ladi, qolganlari ham shu tartibda yoziladi.

2). v₂ ₂   

3). v₃ ₃ 

4). v₄ ₁ ₂ 3.5^//

5). v₅ ₂ ₃  0.5^//

6).v₆ ₁ ₂ ₃ 3.0^//

Ko’rilayotgan masala uchun k=3 nomalumli k chiziqli normal tenglamalar sistemasiga ko’ra tuzatmalar tenglamasi koeffisentlarini 2-jadvalga mos ravishda yozamiz.

2-jadval

Tenglama  lar

a1

a2

a3

l (sek)

s

V//

V//*V//

1

+1

+1

-1.5//

2.25

2

+1

+1

-1.0//

1.00

3

+1

+1

0.0

0.00

4

+1

+1

+3.5

+5.5

+1.0//

1.00

5

+1

+1

+0.5

+2.5

-0.5//

0.25

6

+1

+1

+1

+3.0

+6.0

+0.5//

0.25



a13

a24

a3 3

l7

s17

V

V *V    4.75

Noma’lum lar

1

2

3

a1

a2

a3

l

s

a1i

a1a1 +3

a1a2 +2

a1a3 +1

a1l1 +6.5

a1s1 +12.5

a2i

a2a2 +4

a2a3 +2

a2l2 +7.0

a2s2 +15.0

a3i

a3a3 +3

a3l3 +3.5

a3s3 +9.5

l

l *l +21.5

l *s +38.5

s

s*s +75.5

 

IV¹. Vazn funksiyasini tuzish.

Masalani berilgan shartiga ko’ra 6-burchakning tenglashtirilgan qiymatining aniqligini baholash talab qilingan, shu qiymatni kerakli noma’lumlar orqali ifodalaymiz:

F  x₆  t₁ t₂ t₃ 

bu qiymat 6-tenglamalar bog’liqligidan olingan.

Funksiyaning aniqligini baholashda qo’llanilgan koeffisentlarni yuqoridagi vazn funksiyasini tuzish talablariga asosan topamiz:

f₁ ^^Ft₁ ^₀ 1;      f₂ ^^t^F₂ ^₀ 1;     f₃ ^^t^F₃ ^₀ 1

V.Normal tenglamalarni tuzish.

Chiziqli normal tenglamalar sistemasi quyidagi xususiyatlar bilan farq qiladi: 1) Diagonal bo‘yicha joylashgan chapdan pastga o‘ngga tomon yo‘nalgan koeffitsientlar hamisha musbat sonlardir; ularni kvadratlangan koeffitsientlar deyiladi, ko‘rsatilgan diogonalni esa kvadratli diagonal deb ataladi.

2) Qolgan koeffitsientlari esa kvadratik emas, kvadratli diagonaldan tashqari koeffitsientlar ushbu diagonalga nisbatan simmetrik joylashadi.

Tuzatmalar normal tenglamalarini teng aniqlikdagi o‘lchashlar uchun o‘zida k noma’lumli k chiziqli aniqlangan tenglamalar sistemasini tashkil qiladi

a₁a₁₁ a₁a₂₂ ....a₁a_k _k a₁l 0 

a₁a₂₁ a₂a₂₂ ....a₂a_k _k a₂l 0 ^.

........................................................................._

a₁a_k ₁ a₂a_k ₂ ....a_ka_k _k a_kl 0 _

bu yerda,

a_ia _j  a_1ia_1j a_2ia_{2 j} ....a_nia_nj -_i da va _j da mos holda, tuzatmalar parametrik tenglamalari koeffisiyentlari natijalarining yig`indisi, yoki, matritsa ko‘rinishida

RX  A^TL  0 

bu yerda,  R_A^T _A-normal tenglamalar koeffisiyentlar matritsasi bo`lib u quyidagicha hisoblanadi

a₁a₁.a₁a₂....a₁a_k  

          R  AT  A ..........a1a2...........a2a2..............a2ak..

                                                                                                                               

a1ak .a2ak ....akak 

VI. Tuzatmalarning normal tenglamalar sistemasini yechish. Bunga masalani matematikadagi nomalumlarni ketma-ket yo‘qotishga asoslangan: Xoletskiy, kvadrat ildizlar, Jordan, Gauss, Kramer va boshqa yechish usullaridan foydalanish mumkin. Masalan, Gaussda 3 noma’lumli 3 chiziqli aniqlangan tenglamalar sistemasini yechimidan, kerakli noma’lumlarning taxminiy qiymatiga τ_v tuzatma olinadi: 

a₁a₁₁ a₁a₂₂ a₁a₃₃ a₁l 0 

a₁a₂₁ a₂a₂₂ a₂a₃₃ a₂l ^0_.   -bosh sistema

a₁a₃₁ a₂a₃₂ a₃a₃₃ a₃l 0^_

Tuzatmalar normal tenglamalar sistemasini matritsa ko‘rinishida yechimi quyidagicha bo‘ladi

X R^1 A^TL  0

Bosh tenglamalar sistemasini ekvivalent almashirishlar orqali,  bosh diogonaldan pastdagi koeffisiyentlarni nolga tenglash bilan uchburchak ko‘inishdagi sistemani olamiz, buning uchun bosh tenglamalar sistemasining birinchi tenglamasini _ ^a1a2

a₁a₁

koeffsiyentga ko‘paytiramiz va ikkinchi tenglamaga qo‘shamiz

a a  a1a1a1a21  a2a2 a1a2a1a1a1a22 a2a3 a1a2a1a1a1a33 

               1 2                       a1a1         



a₂l a1aa21a1a1l_  0 _ birinchi noma’lumdagi koeffisiyent nolga teng shunga ko‘ra yozamiz

          _^ a1a2aaa1a2_2 a2a3 a1a2a1a1a1a33 a2l a1aa21a1a1l  0

a2a2

1 1

yoki katta qavslarda Gauss belgilashlarini kiritib quyiagicha yozamiz

a₂a₂.1₂ a₂a₃.1₃ a₂l.1 0

bu yerdagi nuqtadan keying 1(bir) raqami tenglamada ayni shu yergacha nechta nomalum yo‘qotilganlik belgisini beradi. 1(bir) raqam oldidagi koeffisiyent bosh tenglamamadagi koeffisiyentni ayni o‘zi hisoblanadi. 

Xuddi shu tartibda davom ettirib, bosh tenglamalar sistemasining birinchi

tenglamasini  ^a1a3 koeffsiyentga ko‘paytiramiz va uchinchi tenglamaga

a₁a₁

qo‘shamiz

a a  a1a1a1a31 a2a3 a1a2a1a1a1a32  a3a3 a1a3a1a1a1a33 

                1 3                      a1a1         

a₃l a1a_a31_a1a1l_  0

birinchi noma’lumdagi koeffisiyent nolga teng shunga ko‘ra, Gauss belgilashlarini kiritib quyiagicha yozamiz

a₂a₃.1₂ a₃a₃.1₃ a₃l.1 0

Ikkinchi va uchinchi tenglamalarni ikki tenglamali sistema kabi yozamiz

a₂a₂.1₂ a₂a₃.1₃ a₂l.1 0

a₂a₃.1₂ a₃a₃.1₃ a₃l.1 0.

Olingan ikki tenglamali Sistema bilan ekvivalent almashtirishni davom ettiramiz.

Birinchi tenglamani  ^a2a3.1 koeffsiyentga ko‘paytiramiz va natijani ikkinchi

a₂a₂.1

tenglamaga qo‘shamiz

a a  a2a3.1a2a2.12 a3a3.1 a2a3.a12a2.a12a3.13 a3l.1 a2a3a.12a2.1a2l.1  0

     2 3         a2a2.1        



Birinchi koeffisiyent nolga teng ikkinchi noma’lum yo‘qotildi deb, Gauss belgilashlarini kiritib quyiagicha yozamiz

a₃a₃.2₃ a₃l.2 0

Olingan tenglamalarga ko‘ra uchburchak tenglamalar sistemasini quyidagidek olishimiz mumkin

a₁a₁₁ a₁a₂₂ a₁a₃₃ a₁l 0 

.........a₂a₂.1₂ a₂a₃.1₃ a₂l.1 0 ^_-ekvivalent sistema

.............................a₃a₃.2₃ a₃l.2 0^_

Bunday sistemaning koeffisiyentlari Gaussning maxsus sxemasidan olinadi. Bunday sistemani olish prossesi normal tenglamalarni Gauss sxemasida yechishning to‘g‘ri yo‘li deb nomlanadi. Ekvivalent tenglamalar sistemasi oson yechimga ega, darxaqiqat, uchinchi tenglamadan uchunchi noma’lum aniqlanadi. Uni ikkinchi tenglamaga qo‘yib ikkinchi noma’lumni olamiz, ikkita noma’lumga ega bo‘lgan holda birinchi tenglamadan birinchi noma’lumni olamiz. Bu yerda normal tenglamalarni Gauss sxemasida yechishning teskari yo‘lidan foydalaniladi. 

                                                                               a1a2   a1a3   a1l

                                                                   1            2           3 

                                                                               a₁a₁   a₁a₁   a₁a₁

                                                                                       a2a3.1    a2l.1

                                                                           2               3 

                                                                                       a₂a₂.1   a₂a₂.1

a³l.2

₃ 

a₃a₃.2

Oxirgi sistemani elliminatsion normal tenglamalar deyiladi. 

Gauss algoritimimni namoyishining umumiy qoidasini namunada keltirib o‘tamiz

a1a4 a1a5  a2a4.1a2a5.1 a3a4.2a3a5.2

                             a₄a₅.3a₄a₅                                            

                                                                             a₁a₁       a₂a₂.1        a₃a_3..2

Ushbu namunada-Gaussning o‘zgartirilgan algoritimi, o‘zgartirilmagan algoritmdan yo‘qotilgan noma’lumlar soniga mos keladigan kasrlar soni ayirmasiga tengligini ko‘rish mumkin(umumiy hol uchun k, ko‘rilayotgan na’muna uchun 3 ga teng). Kasrlar maxraji tartib bo‘yicha birinchidan k-1 gaha bo‘lgan ekvivalent tenglamalar kvadrat koeffisiyentlariga teng. Kasrlar surati, , harf va indekslari o‘zgartirilmagan algoritm va berilayotgan kasr maxrajidagi algoritm kombinatsiyalaridan tuzilgan ikki algoritmlar natijalaridan iborat.

 Bu sistemada koeffisiyentlar va ozod xadlarning qiymatlari 2-jadvalda berilganlar bo’yicha 3-jadvalda yechiladi. Yechish ketma-ketligi 2-jadvalda ko‘rsatilgandek hisoblanadi. Hamma hisoblashlar quyidagi formula bilan tekshiriladi:

a₁a₁a₁a₂a₁a₃a₁la₁s

 

1) 3 21 6.5 12.5

a₁a₂a₂a₂a₂a₃a₂la₂s

 

2). 2 4 2 7.0 15.0

a₁a₃a₂a₃a₃a₃a₃la₃s

 

3).1 2 33.5 9.5

a₁la₂la₃llllS

 

4). 6.5 7.03.5 21.5 38.5

a₁Sa₂Sa₃SlSSS

 

5).12.515.0 9.538.5 75.5

3-jadval

№	a1a1	a1a2	a1a3	a1l	a1S	a2a2	a2a3	a2l	a2S	a3a3	a3l	a3S	ll	lS	SS
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

 

Funksiyaning aniqligini baholashda quyidagi tekshirishlar yig’indisi kerak bo’ladi:

₁a₁Sa₁l f₁ 12.56.51.0 7.0

₂ a₂Sa₂l f₂ 15.07.01.0 9.0

₃ a₃Sa₃l f₃ 9.53.51.0 7.0

                                                         _ 23.0

Tekshirishlar yig‘indisini hisoblash quyidagi formula bo’yicha tekshiriladi:

^_ f a₁sa₂sa₃sllls3,012,515,09,5 21,538,5 23,5

3-jadvalda berilganlardan foydalanib quyidagi koeffisientlarga ega normal tenglamalar sistemasini olamiz:

3,0₁  2,0₂ 1,0₃  6,5  0  2,0₁  4,0₂  2,0₃  7,0  0^_.

1,0₁  2,0₂  3,0₃  3,5  0 ^_

 Hisoblashdagi ko’nikmalardan keyin oraliq natijalarni yozmasdan normal tenglamalar tuzishning qisqartirilgan (2^a-jadval) sxemasidan foydalanish mumkin.

2^a-jadval

	a1	a2	a3	l	s
a1i	a1a1  3	a1a2 2	a1a3 1	a1l 6.5	a1s 12.5
a2i		a2a2 4	a2a3 2	a2l 7.0	a2s 15.0
a3i			a3a3 3	a3l 3.5	a3s 9.5
l				l *l 21.5	l *s 38.5
s					s*s 75.5

 

 Normal tenglamalarni yechish ekvivalent va eliminatsion tenglamalar qatorlari ketma-ket keladigan Gauss cxemasida 1-ilova jadvalida bajariladi.

Quyida berilgan 1-ilovada noma’lumlarni ketma-ket yo’qotish usuli bilan uchta normal tenglamalarni yechishning harfiy belgilarga ko’ra ko’rsatilgan. Normal tenglamalar yechimining sonli misoli ko’rilayotgan masala uchun 4-jadvalda beriladi. Ikkita oxirgi ustundagi hisoblashlar aniqlikni baholashga bog’liq va normal tenglamalarni yechishning qo’shimcha hisoblari deyiladi. Ularni tushuntirish ulardan oldingi hisoblashlardan keyin amalga oshiriladi( 4-jadval).

          

 

 

 

 

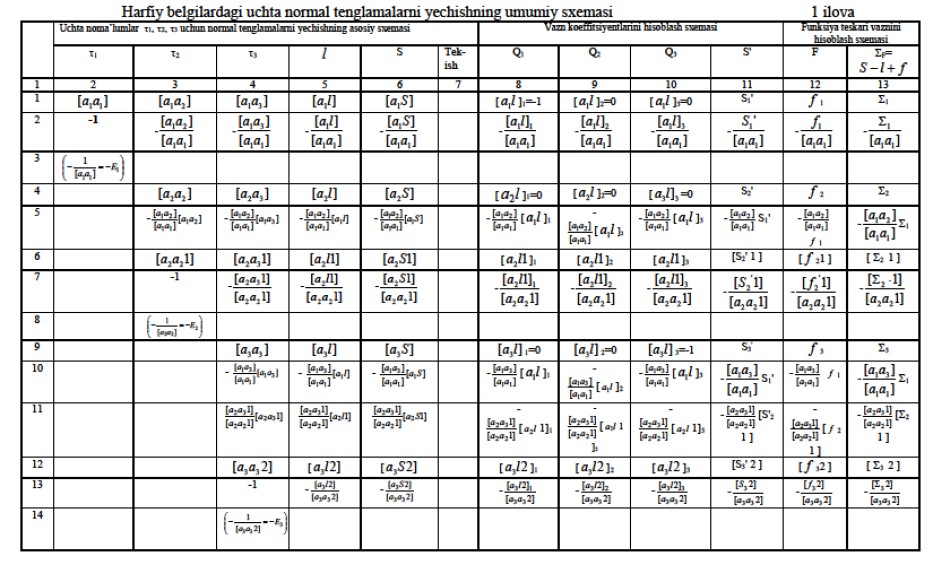
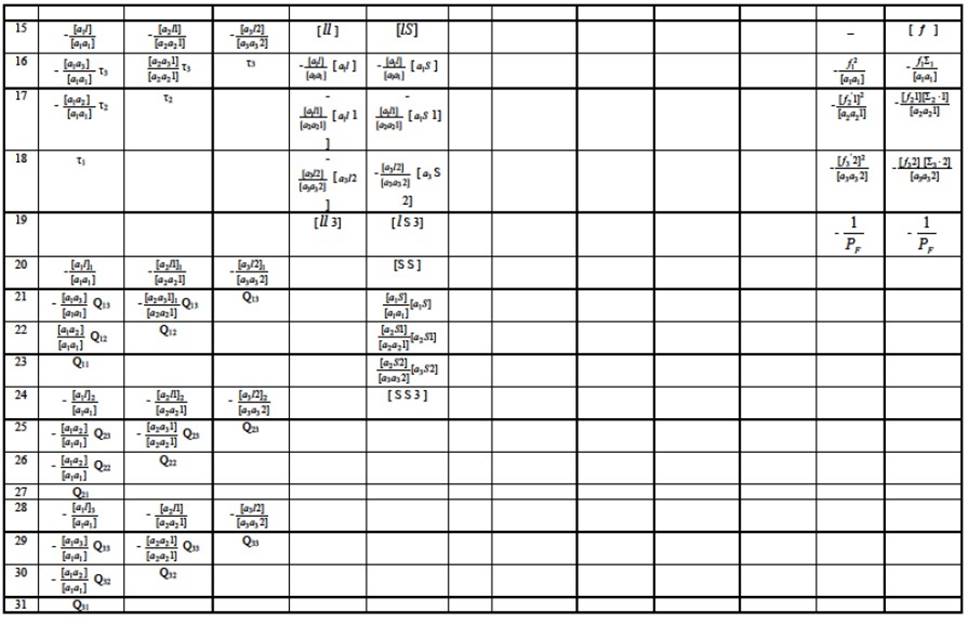
Ko‘rilayotgan masala uchun normal tenglamalarni yechish Gauss cxemasi:

1.                 Bosh sistemaning birinchi tenglamasidagi noma’lumlar koeffisientlari, ozod had va a₁s birinchi qatorga ko‘chirib yoziladi (4-jadval).

a₁a₁a₁a₂a₁a₃a₁la₁s

 

3,00 2,001,00 6,50 12,5

2.                 Birinchi qatorning hamma sonlari kvadrat koeffisiyent a₁a₁ ga bo‘linadi. Hosil bo‘lgan sonlar ikkinchi qatorga teskari ishora bilan yoziladi. Ishorani almashinishi keyinchalik yig‘indilarda ayirishga qo‘l keladi. Bu yerda a₁a₁ 3 ga teng.

4-jadvalning ikkinchi qatorni birinchi eliminatsion qator deyiladi.

Eliminatsion qator koeffisiyentlarini ko‘p marta ishlatiladi. Ularni toppish oson bo‘lishi uchun odatda qizil rangda yozish kerak(dastlabki raqamlar qizil qilib ko‘rsatilgan, 4-jadval 2-qator).

1

Agar foydalanilayotgan bo‘lish jarayoni qiyin bo‘lsa, unda E              qiymatni

a₁a₁ hisoblab 3-qatorga yoziladi. Olingan natijani ketma-ket birinchi qatorga ko‘paytirib 2-qatorga yoziladi. Bizning ko’rib chiqayotgan misol uchun masalan:

                           1        1

E    0.333  bundan, 3*0.333 1; 2*0.333  0.667; 1*0.333  0.333, a₁a₁ 3

6,50*0.333  2,167, 12,50*0.333  4,167.

3.                 Gauss sxemasida yechishda ekvivalent normal tenglamalarini tekshirish uchun quyidagi tekshirish tenglaklari sistemasi qo‘llaniladi

a₁sa₁a₁a₁a₂....a₁a_k a₁l

                                       a₂s.1a₂a₂.1....a₂a_k.1a₂l.1 ^^       _a)

                                                                                                                                                               (3

............................................................... _

a_ks.(k 1)a_ka_k.(k 1)a_kl.(k 1)_

Eliminatsion tenglamalar tekshirish tengliklarini olish uchun yuqoridagi (3^a) sistema tengliklarini har birini “-” ishora bilan mos kvadrat koeffisiyentlariga bo‘lib quyidagi tekshirish tengliklarini olamiz

                                        a¹s 1 a¹a².... a¹a^k  a¹l

-                   

                                       a₁a₁     a₁a₁     a₁a₁ a₁a₁

                                        a²s.1 1 a²a³.1.... a²a^k.1 a²l.1

-                   

                                       a₂a₂.1     a₂a₂.1    a₂a₂.1 a₂a₂.1                      (3^b)

..............................................................

-                   aks.(k 1)^ _1_ a_kl.(k 1)

                                       a_ka_k.(k 1)     a_ka_k.(k 1)

Eliminatsion qator elementlarining birinchi ustundan l ustunigacha har bir qatordagi qiymatlari “tekshirish” ustuniga yig‘indilanadi ((3^a) va (3^b) tengliklarning o‘ng tomoni). “S” ustunga Gauss algoritimlari bo‘yicha hisoblashlar keltirilgan ((3^a) va (3^b) tengliklarning chap tomoni). Ikkala ko‘rilayotgan ustun qiymatlari teng bo‘lishi kerak, bu hisoblashlar xatosiz bajarilganligini belgilaydi. Ya’ni quyidagiga bizning ko’rib chiqayotgan misolda birinchi eliminatsion qatorni tekshirish uchun: a1s       a1a1 a1a2  a1a3   a1l

-                                              

a₁a₁ a₁a₁ a₁a₁ a₁a₁ a₁a₁   4.167 10.667 0.333 2.167

 

-                   4.167 4.167

Bu tekshirish joriy tekshirishni deyiladi va u hamma eliminatsion qatorlarda bajariladi. U verguldan keyin uchta sonning oxirgi raqami qiymatining chekigacha hisoblanadi.

4.   Bosh sistemaning ikkinchi normal tenglamasidagi noma’lumlar koeffisientlari a₂a₂ kvadrat koeffisiyentdan boshlab, ozod had va a₂s to‘rtinchi qatorga ko‘chirib yoziladi.

5.   Birinchi eliminatsion tenglamaning _ ^a1a2_0,667 koeffisiyenti birinchi normal

a₁a₁

tenglamaning a₁a₁ kvadrat koeffisientidan boshqa barcha koeffisientlaiga ko‘paytiriladi. Natija 5-qatorga mos ravishda ikkinchi normal tenglamalar koeffisientlari tagiga yoziladi.

6.   Oltinchi qatorga yuqoridagi 4-va 5-qatorlarning mos ustunlaridagi qiymatlari qo‘shish yo‘li bilan ikkinchi ekvivalent tenglamalarning koeffisiyentlari yoziladi. Ikkinchi ekvivalent tenglama quyidagi ko‘rinishda bo‘ladi

a₂a₂.1₂ a₂a₃.1₃ a₂l.1 0

(3^a) tengliklarga ko‘ra mos holda quyidagicha tekshiriladi

a₂s.1a₂a₂.1a₂a₃.1a₂l.1

Tenglikning o‘g tomonidan olingan natijalar “tekshirish” ustuniga yoziladi.

Ekvivalent va eliminatsion tenglamalar koeffisientlari normal tenglama koeffisiyentlariga qaraganda verguldan keyin bir yoki ikki raqam ortiqcha aniqlikda hisoblanadi.

7.   Oltinchi qator koeffisientlari shu qatorning diagonal elementi _a₂a₂.1 ga bo‘linadi. Olingan natijalar 7-qatorga yoziladi. Eliminatsion qator uchun 3bosqichda berilgan tekshirish tartibi quyidagi tenglik orqali bajariladi a2s.1 1 a2a3.1 a2l.1

- 

                                                                           a₂a₂.1    a₂a₂.1 a₂a₂.1

                                                                             1               

- 2,498 1 0,4981,000

- 2,498 2,498

8.   Bosh sistemaning uchunchi normal tenglamasidagi noma’lumlar koeffisientlari a₃a₃ kvadrat koeffisiyentdan boshlab, ozod had va a₃s to‘qqizinchi qatorga ko‘chirib yoziladi. 

9.   Birinchi eliminatsion tenglamaning _^{a1a3 }_0,333 koeffisiyenti birinchi normal

a₁a₁

tenglamaning a₁a₁ kvadrat va a₁a₂ koeffisientidan boshqa barcha koeffisientlaiga ko‘paytiriladi. Natija 10-qatorga mos ravishda uchinchi normal tenglamalar koeffisientlari tagiga yoziladi. 

Ikkinchi eliminatsion tenglamaning _ ^a2a3.1 _0,498 koeffisiyenti ikkinchi normal

a₂a₂.1

tenglamaning a₂a₂ kvadrat koeffisientidan boshqa barcha koeffisientlaiga ko‘paytiriladi. Natija 11-qatorga mos ravishda uchinchi normal tenglamalar koeffisientlari tagiga yoziladi.

10.            12- qatorga yuqoridagi 9-,10-va 11-qatorlarning mos ustunlaridagi qiymatlari qo‘shish yo‘li bilan uchunchi ekvivalent tenglamalarning koeffisiyentlari yoziladi. Uchinchi ekvivalent tenglama quyidagi ko‘rinishda bo‘ladi

a₃a₃.2₃ a₃l.2 0

(3^a) tengliklarga ko‘ra mos holda quyidagicha tekshiriladi

a₃s.2a₃a₃.2a₃l.2

Tenglikning o‘g tomonidan olingan natijalar “tekshirish” ustuniga yoziladi.

11.            O‘n ikkinchi qator koeffisientlari shu qatorning diagonal elementi a₃a₃.2 ga bo‘linadi. Olingan natijalar 13-qatorga yoziladi. Eliminatsion qator uchun 3bosqichda berilgan tekshirish tartibi quyidagi tenglik orqali bajariladi a³s.2       1 a³l.2

                                                                                       

                                                                                      a₃a₃.2     a₃a₃.2

                                                                                        1          

1,000 1,000 Noma’lumlar va normal tenglamalar soni 3 tadan ortiq bo‘lsa hisoblash jarayoni Gauss sxemasida yuqoridagi berilganlarga mos ravishda davom ettiriladi. Yuqorida yoritilgan  hisoblashlar, Gaussning maxsus sxemasida normal tenglamalarni yechishning to‘g‘ri yo‘li deb nomlanadi.

 

13.            “ Teskari yo’l” deb ataladigan yechish sxemasi bajariladi. Noma’lum tuzatmalar ₁, ₂, _3 larni qiymatlarini hisoblanadi. Bu formulalarning alohida yig’iluvchilari 4-jadvalning pastki chap burchagiga mos ustunlariga yoziladi. ₁, ₂ , _3 qiymatlarni hisoblashda 1-ilovadagi harfiy ifodadan foydalanilib qiymatlar 3jadvaldan olinadi.

                                                                                  a³l *2    0,00     0.000

                                                                    ₃                           

                                                                                 a₃a₃ *2    2,01

                                                            a²a³ *1   a²l *1    0 1.000 1.000

                                                ₂                ₃                  

                                                            a₂a₂ *1   a₂a₂ *1

                                      a¹a²   a¹a³   a¹l   0.667  (0.000)  2.167 1.500

                          ₁            ₂           ₃            

                                      a₁a₁   a₁a₁   a₁a₁

4-jadval

Qator lar	1	2	3	l	S	Tek shirish	F	 F S  l  f
1	+3.00	+2.00	+1.00	+6.50	+12.50		+1	+7
2	-1	-0.667	-0.333	-2.167	-4.167	-4.167	-0.333	-2.333
3	(-0.3333)	(-0.667)	(-0.337)
4		+4.00	+2.00	+7.00	+15.00		+1	+9
5		-1.33	-0.67	-4.33	-8.34		-0.67	-4.67
6		+2.67	+1.33	+2.67	+6.67	+6.67	+0.33	-4.33
7		-1	-0.498	-1.000	-2.498	-2.498	-0.123	-1.622
8		(-0.3745)
9			+3.00	+3.50	+9.50		+1	+7
10			-0.33	-2.17	-4.17		-0.33	-2.33
11			-0.66	-1.33	-3.32		-0.17	-2.16
12			+2.01	0.00	+2.01	+2.01	+0.50	+2.51
13			-1	0.00	-1.000	-1.000	-0.250	-1.250
14			(-0.4975)
15	-2.167	-1.000	0.000	+21.50	+38.00		0.000	+3.000
16	0.000	0.000	3	-14.09	-27.11		-0.33	-2.33
17	+0.667	-1.000		-2.67	-6.66		-0.04	-0.53
18	-1.500	2		0.000	0.000		-0.13	-0.63
19	1		VV	+4.74	+4.73		-0.50	-0.49
20					+75.50		1      PF	1         PF
21					-52.12
22					-16.64
23					-2.00
24				VV	+4.74

 

14.            Aniqlangan noma’lumlar qiymatlarini normal tenglamalarga qo‘yib tenglamalar sistemasini tekshiriladi

3,0₁  2,0₂ 1,0₃  6,5  0  2,0₁  4,0₂  2,0₃  7,0  0^_.

1,0₁  2,0₂  3,0₃  3,5  0 ^_

3,0(1,500)  2,0(1,000) 1,0(0,000)  6,5  0  2,0(1,500)  4,0(1,000)  2,0(0,000)  7,0  0^_.

1,0(1,500)  2,0(1,000)  3,0(0,000)  3,5  0 _^

4-jadvalning oxiridan oldingi ustunida normal tenglamani yechish bilan bir vaqtda quyidagi

formulani qo’llab F  x₆  t₁ t₂ t₃ funksiyasining teskari vazni hisoblanadi:

 

4-jadvalning oxirgi ustunidagi funksiyaning teskari vazni tekshiruv formulasi bo’yicha olingan

 

VII.      O’lchangan natijalarga tuzatmalarni hisoblash.

 O’lchangan burchaklar qiymatiga v_i  tuzatma tuzatmalarning parametric tenglamasi bo’yicha 2-jadvaldan topiladi va ushbu jadvalni tuzish tugatiladi. 

1).v₁ ₁  1.5^// 

2). v₂ ₂  1.0^//   

3). v₃ ₃  0.000 

4). v₄ ₁ ₂ 3.5^// 1.51.03.5 2.53.5 1.00^//

5). v₅ ₂ ₃  0.5^//  1 0.0 0.5^//  1 0.5^//  0.5^//

6).v₆ ₁ ₂ ₃ 3.0^//  1.51.003.0^//  2.53.0^//  0.5^//

Shuningdek quyidagi tenglik tekshiriladi:

 

VIII.   Nomalumlarning(parametrlarning) tenglashtirilgan qiymatini hisoblash.

 Biz ko’rib chiqilayotgan misolda parametrlar sifatida o’lchangan miqdorlar tanlangan, shuning uchun ko’riladigan hisoblarni keying bosqichdagi hisoblar bilan birgalikda bajarish maqsadga muvofiqdir.

VIII¹. O’lchangan miqdorlarning tenglashtirilgan qiymatini hisoblash.

5-jadvalda v_i  tuzatmadan foydalangan holda o’lchangan burchaklarning tenglashtirilgan qiymatlari hisoblanadi:

5-jadval

 

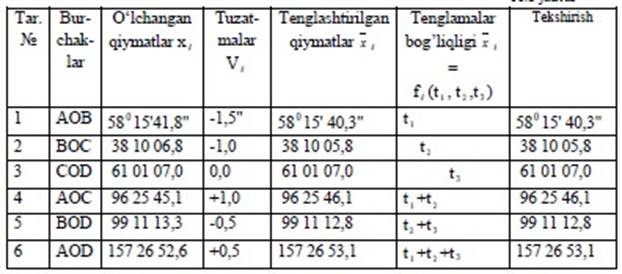
IX.          Tenglashtirishning yakuniy tekshirishi.

 Yakuniy tekshirish  xi  x₁ v_i  f_i (t₁,t₂,t₃) tenglamalar bog’liqligiga ko’ra, burchakning tenglashtirilgan qiymatini qaytadan hisoblashdan iborat bosqich hisoblanadi. Bu tekshirish hisoblari 5-jadvalning oxirgi ikkita ustunida bajariladi. X. Aniqlikni baholash.