Решение задач на нахождение площадей и объёмов многогранников

Тема: «Многогранники. Их поверхности и объемы».

Авторы работы:
научный руководитель - Кобаидзе Нина Ивановна,
учитель математики и учащиеся – 9-10 классов

Место выполнения работы - МБОУ ордена «Знак Почёта» им. А. В. Луначарского гимназия №5

классы: 10 “А” и 9 “А”

город - Владикавказ, РСО-А

страна – РФ

Научный руководитель: Кобаидзе Нина Ивановна, учитель математик

Творческая работа

1. В теме «Многогранники» помимо общего стереометрического чертежа рекомендуется выполнять вспомогательные планиметрические чертежи тех элементов многогранника, которые рассматриваются при решении данной задачи (оснований, боковых граней, сечений).

Надо отчетливо находить различие в определении прямой и правильной призм, прямого и прямоугольного параллелепипедов. Уяснить, что квадрат диагонали равен сумме квадратов трех измерений только в прямоугольном параллелепипеде. При вычислении боковой и полной поверхностей многогранников надо помнить, что боковая поверхность неправильной пирамиды вычисляется как сумма площадей боковых граней. Твердо уяснить, куда проектируется вершина пирамиды, если ее ребра равнонаклонены и углы наклона боковых граней к плоскости основания равны. Если в пирамиде углы наклона боковых граней к плоскости основания равны, то высота пирамиды проектируется в центр окружности, вписанной в основание пирамиды. Если в пирамиде все ребра равнонаклонены к плоскости основания, то высота пирамиды проектируется в центр окружности, описанной около основания пирамиды.

Для определения боковой и полной поверхностей пирамиды с равнонаклоненными гранями к плоскости основания нужно знать такие формулы:

( – угол наклона боковых граней к плоскости основания).

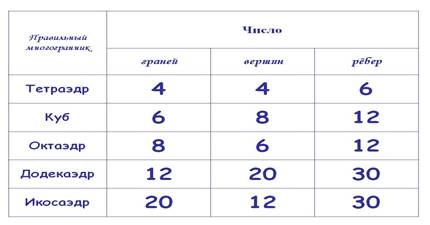
О правильных многогранниках

2. В понятии правильного многогранника, должны выполняться два условия, входящие в определение правильного многогранника: a) все грани такого многогранника – равные правильные многоугольники; б) в каждой вершине многогранники сходится одно и то же число ребер.

3. В учебнике доказано, что существует только пять видов правильных многогранников и не существует правильного многогранника, гранями которого являются правильные n-угольники при n ≥ 6.

Угол правильного многоугольника вычисляется по формуле При каждой вершине многогранника не меньше трех плоских углов и их сумма должна быть меньше 360°.

При n = 3, когда гранями многогранника служат правильные треугольники, имеем .

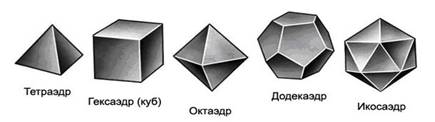
В соответствии с этим получаем правильные многогранники, изображенные на рисунках 81, 82, 83: правильные тетраэдр, октаэдр, икосаэдр.

Если n = 4, то , грани многогранника квадраты. Поэтому в этом случае получаем только один правильный многогранник – куб (рис. 84).

Если n = 5, т.е. грани многогранника правильные пятиугольники, то и поэтому в этом случае также имеем только один правильный многогранник – додекаэдр (рис. 85).

Если , то , и следовательно, не существует правильного многогранника, гранями которого служат правильные n угольники при

n ≥ 6.

Задача №1. Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 30° и 45°. Найдите площадь поверхности пирамиды.

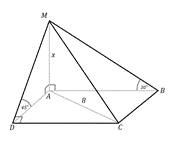Рис. 1

Решение. 1. Предположим, что плоскости М AB и М AD перпендикулярны к плоскости основания, тогда линия их пересечения М A перпендикулярна к плоскости основания, т.е. M A – высота пирамиды (рис. 1).

2. Так как , то по теореме о трех перпендикулярах, поэтому ∠MBA – линейный угол двугранного угла при ребре CB, ∠MBA = 30°.

Аналогично:

, , MDA – линейный угол двугранного угла при ребре DC, ∠MDA = 45. Треугольники MBC и MDC – прямоугольные.

3. Пусть MA = x см, тогда MB = 2x см, AB = .

Из ΔMAD: MA = AD = x см, .

Из ΔABC:

4. Таким образом: MA = 4 см, AB = DC = 4(3) см, MB = 8 см, MD = , AD = BC = 4 см.

Ответ:

Задача №2. Основанием наклонной призмы служит правильный треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ с. Определить объем призмы (рис. 2).

Дано: наклонная призма, - правильный, |AC| = a, AA₁B₁B – ромб, AA₁B₁B┴, |A₁В|=с.

Определить V_пр.

Рис. 2

Решение. Известно, что V_пр=S_оснH. Площадь основания призмы находим по формуле , т.е.,

Высотой призмы будет отрезок [A₁K], так как если две плоскости перпендикулярны и к одной из них (пл. ABC) проведен перпендикуляр, имеющий общую точку (А₁) с другой плоскостью (AA₁B₁B), то он весь лежит в этой плоскости. Для определения [A₁K], рассмотрим два прямоугольных треугольника AKA₁ и A₁KB. Пусть |AK|=x, тогда |KВ|=a-x;

|A₁K|²=|AA₁|²-|AK|²;|A₁K|²=|A₁B|²-|KB|²; |AA₁|²-|AK|²=|A₁B|²-|KB|²;

a ²- x²=c²-(a-x)²; a²-x²=c²-a²+2ax-x²;

2ax= 2а² - c²;

;

Таким образом, объем призмы

= .

Задача №3. В прямом параллелепипеде с основанием ABCD |AB|=29 см, |AD|=36 см, |BD|=25 см и боковое ребро равно 48 см. Определить площадь сечения AB₁C₁D.

Дано: прямой параллелепипед ABCDA₁B₁C₁D₁ (рис. 21), |AB|=29 см, |AD|=36 см, |BD|=25 см, |AA₁|=48 см, сечение AB₁C₁D.

Определить: S_сеч.

Решение. Сечение AB₁C₁D – параллелограмм, так как в четырехугольнике AB₁C₁D стороны B₁C₁ и AD равны и параллельны.

Рис. 3

Площадь параллелограмма равна произведению высоты на основание. В основании параллелепипеда лежит параллелограмм ABCD. Проведем в нем [BF]┴[AD] и точку F соединим с точкой B₁. Тогда

[B₁F] есть наклонная к плоскости ABCD, BF ее проекция на эту плоскость. Если прямая AD, лежащая в плоскости перпендикулярна и самой наклонной BF на эту плоскость, то она перпендикулярна и самой наклонной B₁F (теорема о трех перпендикулярах) – B₁F┴AD, следовательно, B₁F – высота сечения, отсюда

S_сеч=|AD||B₁F|.

Определим |BF₁| из треугольника BB₁F, в котором сначала надо определить отрезок |BF|, являющийся высотой треугольника ABD. Высоту треугольника определим по формуле (площадь ΔABD вычислим по формуле Герона), тогда получим

|BF|==20.

Треугольник BFB₁ – прямоугольный, так как в прямом параллелепипеде боковые ребра перпендикулярны плоскости основания. По теореме Пифагора имеем

;

S_сеч = 3652( см²) = 1872 см².

Задача №4. Вычислить полную поверхность правильной четырехугольной пирамиды, высота которой H=3,1 м, а апофема составляет с основанием угол β=60 (рис. 4).

Дано: SABCD – правильная пирамида, |SO|=H=3,1 м, .

Определить S_П.

Решение. S_П = S_бок + S_осн;

Рис. 4

Из прямоугольного треугольника SOK имеем

|SK|=

(OK лежит против );

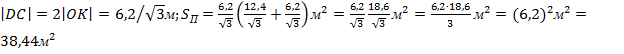Задача №5. В треугольной пирамиде стороны основания равны 13, 14, 15, а двугранные углы при основании равны каждый . Найти площадь боковой поверхности пирамиды.

Решение. . Площадь основания определяем по формуле Герона

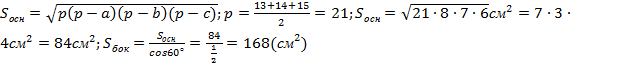Задача №6. Стороны оснований правильной треугольной усеченной пирамиды равны 5 и 2 дм, боковое ребро 2 дм. Найти высоту и апофему пирамиды (рис. 5).

Дано: ABCA₁B₁C₁ - правильная усеченная пирамида, |AB|=5 дм, |A₁B₁|= 2 дм, |AA₁|=2 дм.

Определить: |OO₁| - высоту и |HH₁| - апофему пирамиды.

Решение. Дополнительные построения. Чтобы найти длину высоты OO₁, надо связать ее метрическим соотношением с другими отрезками, длины которых известны. Для этого проводим высоту
Рис. 5

из точки A₁, а чтобы найти апофему, проводим высоту из точки H₁, Из ∆AKA₁ находим

|A₁K|= (1)

Рис. 5

(2)

, значит, .

Аналогично .

Подставим найденные значения |OA| и |OK| в (2)

Подставим значения |AA₁| и |AK| в (1):

, но |OO₁|=A₁K, значит, высота |OO₁|=1дм.

Из ∆MH₁H имеем (3)

Найдем |MH|:

|MH|=|OH|-|O₁H₁| (4)

|OH|= (медианы делятся в отношении 1:2).

Значит, .

Аналогично, .

Подставим значения |OH| и |O₁H₁| в (4):

Подставим значения |MH₁| и |MH| в (3):

Задача №7. Стороны оснований правильной четырехугольной усеченной пирамиды соответственно равны 8 и 6 см. Двугранный угол при ребре основания равен . Определить площадь боковой поверхности усеченной пирамиды.

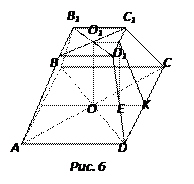Дано: A-C₁ – правильная усеченная пирамида, |DC|’=8 см, |D₁C₁|’=6 см, (рис. 6).

Определить S_бок.

Решение. .

В трапеции OO₁MK имеем |O₁M|=3 см, |OK|=4 см. Из ∆MEK: |MK|=2|EK| (EK лежит против угла в ); |MK|=2 см.

2019 – 2020 г.

Кобаидзе Н. И

Решение задач на нахождение площадей и объёмов многогранников

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

28.12.2019