Решение задач на смеси, растворы и сплавы

Решение задач на смеси, растворы и сплавы

 В числе текстовых задач особое место занимают задачи на смеси, растворы и сплавы, называемые еще задачами на процентное содержание или концентрацию, наличие в которых простых и процентных отношений зачастую побуждает относить их к разряду чисто арифметических, а не к задачам на составление уравнений.

Вместе с тем такие задачи можно решать составлением уравнений или их систем по схеме, очень близкой к той, что применяется в задачах на движение, работу и др.

Как известно, в основе методики решения этих задач лежит связь  между тремя величинами в виде прямой или обратной зависимостей:

 – для пути  s,  времени  t  и скорости  v;

 – для количества работы А, времени  t  и производительности  v.

В аналогичных соотношениях находятся стоимость, цена и количество.

Кроме того, применяются некоторые правила: сложение или вычитание скоростей при движении в движущейся среде, сложение или вычитание производительностей при совместной работе и др.

Приведенная ниже методика решения задач на смеси, растворы и сплавы, опирается на такие же зависимости и правила.

а) Основные понятия в задачах на смеси, растворы и сплавы

Прежде всего, введем основные понятия. Говоря о смесях, растворах и сплавах, будем употреблять термин «смесь» независимо от ее вида (твердая, жидкая, газообразная, сыпучая и т. д.). Смесь состоит из «чистого вещества» и «примеси». Что есть «чистое вещество», определяется в каждой задаче отдельно, однако при этом все остальные вещества, составляющие смесь, относят к примеси. Долей  () чистого вещества в смеси называется отношение количества чистого вещества  (m)  в смеси к общему количеству  (М)  смеси при условии, что они измерены одной и той же единицей массы или объема:

Отсюда получаем    

Отметим, что   ввиду того, что  Случай =0  соответствует отсутствию выбранного чистого вещества в рассматриваемой смеси  (m=0), случай =1  соответствует тому, что рассматриваемая смесь состоит только из чистого вещества  (m = М). Понятие доли чистого вещества в смеси можно вводить следующей условной записью:

Доля чистого вещества в смеси =

Количество чистого вещества в смеси

Общее количество смеси

Процентным содержанием чистого вещества в смеси  (с)  называют его долю, выраженную процентным отношением:

При решении задач следует руководствоваться тем, что при соединении (разъединении) смесей с одним и тем же чистым веществом количества чистого вещества и общие количества смесей складываются (вычитаются). Складывать и  вычитать доли и процентные содержания нельзя.

б) Основные этапы решения задач

1.                 Выбор неизвестной (или неизвестных). Чаще всего в качестве неизвестных величин выбирают те, которые требуется найти, но иногда целесообразно обозначать неизвестными промежуточные величины, через которые легко выражаются искомые.

2.                 Выбор чистого вещества. Из веществ, фигурирующих в условии задачи, выбирается  одно в качестве чистого вещества. Чаще всего выбирают вещество, о котором идет речь в требовании задачи, или вещество, о доле которого в условии содержится больше всего информации. При этом, если   –  доля чистого вещества, то (1 – ) – доля примеси.

3.                 Переход к долям. Если в задаче имеются процентные содержания, их следует перевести в доли и в дальнейшем работать только с долями.

4.                 Отслеживание состояния смеси. На каждом этапе изменения смеси (добавление, изъятие) необходимо описывать состояние смеси с помощью основных величин  m,  М,  .

5.                 Составление уравнения. В результате преобразований смеси, описанных в задаче, придем к ее итоговому состоянию. Оно характеризуются величинами  m,  М,  , содержащими неизвестные. Уравнением, связывающим эти неизвестные, будет уравнение 

В ходе осуществления этих этапов рекомендуется ввести следующую таблицу.

Таблица 6

6. Решения уравнения (или их системы) и на хождение требуемых величин.

7.                 Формирование ответа. Если в задаче требовалось найти то или иное процентное содержание, то следует полученные доли перевести в процентные содержания.

Далее проиллюстрируем перечисленные этапы на примерах.

в) Примеры решения задач

Задача 2.33.  Морская вода содержит 5% соли по массе. Сколько пресной воды  нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?

Решение.

1. Пусть требуется добавить x кг пресной воды.

2. За чистое вещество примем соль. Тогда морская вода – это смесь с 5%-ным содержанием чистого вещества, пресная вода – с 0%-ным содержанием чистого вещества.

3. Переходя к долям, получаем, что доля соли в морской воде составляет 0,05,  доля соли в пресной воде равна 0, доля соли в смеси, которую нужно получить, – 0,015.

 4. Происходит соединение смесей  (табл. 7).

Таблица  7

5. Исходя из третьей строки табл. 2, составим уравнение 

 = 0,015(30 + x).

6.     Решаем полученное уравнение и находим x = 70.

7.     В данной задаче не содержалось требования найти процентное содержание какого-либо вещества, поэтому нет необходимости переводить доли в процентные содержания.

Ответ:  70 кг.

Задача 2.34. Сколько килограммов воды нужно выпарить из 0,5 т целлюлозной массы, содержащей 85% воды, чтобы получить массу с содержанием 25%  целлюлозы?

Решение.

1. Пусть x т воды следует выпарить.

2. За чистое вещество принимаем сухую целлюлозу.

3. Доля воды в данной целлюлозной массе 1 – 0,85 = 0,15. Выпаривается чистая вода, в ней доля целлюлозы равна нулю. Доля целлюлозы в смеси после выпаривания – 0,25.

4. Происходит разъединение смесей (изъятие из данной смеси воды выпариванием)  (табл. 8).

Таблица  8

5. Составим уравнение вида  по третьей строке табл. 8:

6. Решая уравнение, получим x = 0,2.

7. Следует выпарить 0,2 т воды. В соответствии с требованием задачи переводим ответ в килограммы.

Ответ: 200 кг.

Решим эту же задачу, выбрав в качестве чистого вещества воду.

1. Пусть x т воды следует выпарить.

2. За чистое вещество принимаем воду.

3. Доля воды в данной массе – 0,85. Доля воды в выпаренной воде будет составлять 1. Доля воды в полученной смеси составит 1 – 0,25 = 0,75.

4. Происходит изъятие из данной смеси воды (выпариванием)  (табл. 8).

Таблица  9

5–6. Составим уравнение по третьей строке табл. 9 и решим его

 = (0,5 - x)0,75,

x = 0,2.

Ответ: 200 кг.

Комментарий. По мере приобретения навыков учащимся необязательно выделять записями указанные этапы решения. После выбора неизвестных они составляют таблицу, в процессе заполнения которой реализуются этапы 2,3 и 4.

Задача. Смешали 30%-ный раствор соляной кислоты с 10%-ным и получили 600 г 15%-ног раствора. Сколько граммов каждого раствора было взято?

Решение. Пусть взяли x г первого раствора, тогда второго раствора (600 - x) г  (табл. 10).

Таблица  10

Тогда 0,3 x +0,1(600 – x) = , откуда x = 150, 600 - x = 450.

Ответ: 150 г  30%-ного раствора, 450 г  10%-ного раствора.

Комментарий. При решении задач на составление уравнений задача может сводиться не к одному уравнению, а к системе уравнений. К этому подталкивает и текст задачи, по которому требуется найти несколько неизвестных величин. Какие-то из уравнений системы будут составлены на основе таблицы состояний смесей, а какие-то – на основе двух взаимосвязей величин, описываемых в задаче. Так, например, предыдущую задачу можно решить следующим образом: пусть x г первого раствора и взяли у г второго раствора, тогда по условию задачи 

x + у = 600   (табл. 11).

Таблица  11

Из табл. 7 получаем еще одно уравнение

0,3 x +0,1у = 0,15(x + у)

и задача сводится к решению системы

Задача.  Сплав меди с серебром содержит серебра на 1845 г больше, чем меди. Если бы к нему добавили некоторое количество чистого серебра, по массе равное   массы чистого серебра, первоначально содержащегося в сплаве, то получился бы новый сплав, содержащий  83,5%  серебра. Какова масса сплава и каково первоначальное процентное содержание в нем серебра?

Решение. Пусть масса сплава – x г, а доля чистого серебра в нем – . Тогда количество серебра в сплаве равно x г, количество меди –  (x – x) г.

По условию x = x – x + 1845.

Таблица  12

Составим систему уравнений и решим ее:

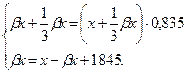
Получим

Сформулируем ответ к задаче. В соответствии с обозначениями масса сплава равна 3165 г, а доля чистого серебра в нем   0,791. Выразим долю в процентах.

Ответ: 3165 г,   79,1%.

Как и в других текстовых задачах, задача на смеси может приводить к системе уравнений, в которой число введенных неизвестных больше числа уравнений, которые можно составить по сюжету задачи.