Решение задач с помощью рациональных неравенств

Урок 3/30.                       

Тема урока: Рациональные неравенства. Решение задач с помощью рациональных неравенств.

  Вид урока: обобщение знаний.                                                             

Тип урока: « Открытие» нового знания.

 Цели урока:

Предметные: ввести понятие рационального неравенства с одной переменной; создать условия для формирования представлений об алгоритме решения рациональных неравенств; использовать рациональные задачи при решении текстовых задач; научить применять метод интервалов к решению рациональных неравенств; способствовать развитию математической речи; воспитывать культуру поведения при фронтальной работе, работе в группах, индивидуальной работе.

Коммуникативные: уметь договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов, участвовать в коллективном обсуждении проблем.

Регулятивные: различать способ и результат действия, оценивать правильность выполнения действия, умение учиться и способность к организации своей деятельности; создать условия для развития умения анализировать, обобщать изучаемые факты, рефлексии способов и условий действия.

Познавательные: осуществлять поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы; владеть общим приемом решения рациональных неравенств,

Личностные: формирование познавательного интереса.

Оборудование: компьютер, проектор, презентация, карточки с заданиями для групп.

Ход урока

I. Организационный момент.

 — Здравствуйте, ребята! Садитесь. Древняя китайская мудрость гласит: «Я слышу – я забываю, я вижу – я запоминаю, я делаю – я понимаю». И сегодня я вас призываю следовать этой мудрости и предлагаю поработать на уроке по принципу

«Я слышу – я вижу – я делаю»

II. Актуализация знаний обучающихся.

Вы видите на доске  алгебраические выражения. Как они называются?  

1.(х ‒ 1)(х ‒ 2)(х ‒ 3) > 0

2.(х ‒ 1)³(х ‒ 2)²(х ‒ 4) ˂ 0

3.    

4.  ˂0.

— Какие неравенства называются рациональными?

— Каким способом они решаются?

Класс разделен на 5  групп по 4 человека. Каждой группе предложена карточка с заданиями:

Карточка для I группы.

1.   Решить рациональное неравенство  >0

2.      Определить вид данного неравенства.

3.      Записать алгоритм решения неравенства.

4.      Найти «похожее» неравенство в самостоятельной работы.

Карточка для II группы.

1.   Решить рациональное неравенство  ˂0

2.      Определить вид данного неравенства.

3.      Записать алгоритм решения неравенства.

4.      Найти «похожее» неравенство в самостоятельной работы.

Карточка для III группы.

1.   Решить рациональное неравенство  >0

2.      Определить вид данного неравенства.

3.      Записать алгоритм решения неравенства.

4.      Найти «похожее» неравенство в самостоятельной работы.

Карточка для IV группы.

1.   Решить рациональное неравенство  >

2.      Определить вид данного неравенства.

3.      Записать алгоритм решения неравенства.

4.      Найти «похожее» неравенство в самостоятельной работы.

Карточка для V группы.

1.   Решить рациональное неравенство  ˂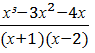

2.      Определить вид данного неравенства.

3.      Записать алгоритм решения неравенства.

4.      Найти «похожее» неравенство в самостоятельной работы.

Участник от каждой группы выходит к доске и решает предложенное заданиение, остальные устно отвечают на вопросы.

III.   Контроль знаний.

 Самостоятельная работа

I вариант

1.   >0

2.   >0

3.   ˂0

4.   ˂

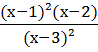5.   >0

II вариант

˂0

2.  ˂0

3.  >0

4.  ˂

5.  ˂0

Учащиеся выполняют самопроверку по готовым ответам.

IV. «Открытие» новых знаний. 

    — Ребята, какой способ мы часто используем при решении задач?

— Как вы думаете, можно ли решать задачи при помощи неравенств?

Учащиеся решают заранее приготовленные задачи.

1. Первая бригада может выполнить задание на два дня раньше второй и на восемь дней раньше третьей. Но если вторая и третья бригады будут работать вместе, то выполнят задание не позже первой бригады. За какое наименьшее время первая бригада может выполнить задание?

2. Первая труба наполняет бассейн на 4 часа быстрее второй и на 9 часов быстрее третьей. Даже если наполнять бассейн через вторую и третью трубы одновременно, то бассейн заполняется не быстрее, чем через первую трубу. За какое наибольшее время первая труба может заполнить бассейн?

3. Из пункта А выехал велосипедист и прибыл в пункт В через 3 часа. Одновременно с ним из В в А выехал мотоциклист и вышел пешеход. Скорость мотоциклиста на 12 км/ч больше скорости велосипедиста, а скорость пешехода на 6 км/ч меньше скорости велосипедиста. Найдите наибольшую скорость велосипедиста, если известно, что между встречами велосипедиста с мотоциклистом и пешеходом прошло не менее 1 часа.

— Одну из подобных задач я предлагаю вам для домашнего задания:

     От пола комнаты одновременно вертикально вверх по стене поползли две мухи. Поднявшись до потолка, они поползли обратно. Первая муха ползла в оба конца с одной и той же скоростью, а вторая хотя и поднималась вдвое быстрее первой, но зато спускалась вдвое медленнее. Какая из мух раньше приползет обратно?

V.  Подведение итогов.

 1. Как называются неравенства, которые мы сегодня решали?
2. Какой способ мы использовали при их решении?
3. Что нового узнали на этом уроке?
4. Можно ли применять решение неравенств в практических целях? Если да, то для каких целей?

Домашнее задание.

От пола комнаты одновременно вертикально вверх по стене поползли две мухи. Поднявшись до потолка, они поползли обратно. Первая муха ползла в оба конца с одной и той же скоростью, а вторая хотя и поднималась вдвое быстрее первой, но зато спускалась вдвое медленнее. Какая из мух раньше приползет обратно?

Из учебника: № 176 – 178 (б, г).

Скачано с www.znanio.ru