Содержание

 

Уравнения. Решение уравнений .................................................................................................. 2

Решение текстовых задач ............................................................................................................. 3

Решение неравенств и систем неравенств .................................................................................. 5

Арифметический квадратный корень и его свойства ................................................................ 8

Преобразование выражений, содержащих квадратные корни ............................................... 11

Формулы корней квадратного уравнения. Решение квадратных уравнений.   Уравнения, сводящиеся к квадратным................................................................................................................................... 13

Решение систем уравнений второй степени ............................................................................. 19

Квадратичная функция. Построение графиков квадратичной функции ............................... 22

Квадратные неравенства ............................................................................................................. 26

Список литературы...................................................................................................................... 29

 

             

Уравнения. Решение уравнений.

Уравнением называют равенство, в котором неизвестное обозначено буквой. Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения.

Решить уравнение – значит найти все его корни или убедиться, что это уравнение не имеет ни одного корня.

 

Правила решения уравнений.

Правило 1. Корни уравнения не изменятся, если какое-нибудь  слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный.

Примеры:

а) 3х – 8 = х – 14                                                    _{б) – 2(3х + 4) =} - 10 _{– 8х}

3х – х = - 14 + 8         - 6х – 8 = - 10 – 8х 2х = - 6   - 6х + 8х = - 10 + 8 х = - 6 : 2    2х = - 2 х = - 3           х= - 1

_{Ответ: х =} - 3.                                                          Ответ: х = - 1.

 

в) - 0,1(х – 0,5) = 0,2(3 – 5х)

    - 0,1х + 0,05 = 0,6 – х

    -0,1х + х = 0,6 - 0,05

    0,9х = 0,55     х = ^0,55     х =  

90

    х = ¹¹

Ответ:    х =             .

 

Правило 2. Корни уравнения не изменятся, если обе части умножить или разделить на одно и то же число, не равное нулю. Примеры:

а) 10х – 120 = 30х – 40

Разделим каждое слагаемое обеих частей уравнения на 10.

х – 12 = 3х – 4 - 2х = 8 х = - 4

 Ответ: х = - 4.

 

б) 1 х - ¹ = ⁵ - ⁸х

      2             3         18       9

Умножим каждое слагаемое обеих частей уравнения на 18. х

9х – 6 = 5 – 16х,  9х + 16х = 5 + 6,  25х = 11,  х = 0,44 Ответ: х = 0,44.

Решение текстовых задач.

 

Задача 1. Зарплату токарю повысили сначала на 10%, а затем, через год, ещё на 20%. На сколько процентов повысилась зарплата токаря по сравнению с первоначальной?

 

Решение.

Пусть а – первоначальная зарплата; а + 0,1а = 1,1а – новая зарплата; 1,1а · 0,2 = 0,22а – новое повышение;

1,1а + 0,22а = 1,32а – зарплата после второго повышения;

(1,32𝑎−𝑎) ∙100%

 = 32% - на столько повысилась зарплата.

𝑎

Ответ: зарплата повысилась на 32%.

 

Задача 2. Некоторый товар вначале подорожал на 10%, а затем подешевел на 10%. Как изменилась цена товара?

 

Решение. а – первоначальная цена; а + 0,1а = 1,1а – цена после подорожания; 1,1а - 1,1а · 0,1 = 0,99а – окончательная цена;

(𝑎−0,99𝑎)∙100%

 = 1% - на столько уменьшилась цена.

𝑎

Ответ: цена уменьшилась на 1%.

 

Задача 3. От пристани А отошёл теплоход со скоростью 45 км/ч. Через 45 минут от пристани В навстречу ему отошёл второй теплоход, скорость которого 36 км/ч. Расстояние между пристанями А и В равно 162 км (движение в стоячей воде). Через сколько часов после отправления первого теплохода они встретятся?

 

Решение.

Пусть х (ч) – время до встречи первого теплохода, тогда (162 – 45х) (км) –

162−45х расстояние, которое пройдет второй теплоход до встречи;  (ч) – время в пути до

36

встречи второго теплохода. 

По условию задачи известно, что второй теплоход был в пути на 45 мин меньше, т.е.

162−45х

 < х на  , поэтому составляем уравнение:

36

 

 162−45х = х - 

36

162 – 45х = 36х – 27

81х = 189 х = 2.

Итак, через  2 часа после отправки первого теплохода они встретились.

 

Ответ: через 2 часа

Задачи на равномерное движение.

 

Решая задачи на равномерное движение, полезно делать наглядную схему, иллюстрируя сюжет задачи. Помимо традиционно использующихся в задачах величин: скорость, время и расстояние – необходимо уметь выражать скорости сближения или удаления объектов. Надо различать 4 типа задач:

 

1)                 встречное движение:            V1                                                                                           V2

 АВ = s

А                                                                        В

                                                                        через t часов Vсближения = V1 + V2 =  𝑠.

𝑡

 

2)                 движение удаления: 

 АВ = s

А                                                              В

через t часов

Vудаления = V1 + V2 =  𝑠.

𝑡

 

3)                 движение вдогонку: 

   А                                   В

АВ = s                                                                                                    через t часов

 

Vсближения = V1 - V2 =  𝑠.

𝑡

 

4)                 движение обгона:                                               V₂                        V₁ 

А      s       В    через t часов

Vудаления = V1 - V2 =  𝑠.

𝑡

При решении необходимо разбить её на типовые задачи, для каждой из которых нетрудно составить уравнение.

В задачах на движение по реке (в потоке воздуха, на эскалаторе и т.д.) полезно

помнить формулы:

 

Vпо течению = Vсобств. + Vтечения

 

V_{собств.} = Vпо течению+Vпротив течения   

2

 

 

Vпротив течения = Vсобств. - Vтечения

 

V_{течения.} =  𝑉по течению− Vпротив течения  .

2

 

 

Решение неравенств и систем неравенств.

 

Линейное неравенство с одной переменной x  – это неравенство вида a ⋅ x + b > 0, когда

вместо >  используется любой знак неравенства <,   ≤,   ≥,   а и b  являются действительными числами, где a ≠ 0.

Решить неравенство – значит найти все значения переменной, при которых неравенство обращается в верное числовое неравенство.

Свойство 1. Если a > b и b > c, то  a > c.

Свойство 2. Если a  > b, то  a + c > b + c.

Если к левой и правой частям неравенства прибавить одинаковое число, то знак неравенства не изменится.

Свойство 3. Если a > b и k > 0, то ak > bk.

При умножении левой и правой частей неравенства на одинаковое положительное число знак неравенства не изменяется.

Свойство 4. Если a > b и k < 0, то ak < bk.

При умножении обеих частей неравенства на одно и то же отрицательное число знак неравенства нужно заменить (< на >, >  на  <).

1 Деление на число k можно заменить умножением на дробь .

𝑘

Пример 1.

 3x + 12 ≤ 0

3x ≤ −12

(3x) : 3 ≤ (−12) : 3  x ≤ − 4

Ответ: (−∞, −4].  Пример 2. 

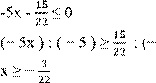5 ) 

Ответ: [

Пример 3.

5·(x + 3) + x ≤ - 6·(x − 3) - 1 

5x  + 15 + x ≤ - 6x + 18 - 1 

6x + 15 ≤ - 6x +17 

6x + 6x ≤ 17 -15  

12x ≤ 2

х  

Ответ: .

Пример 4.

5·(x + 3) + x ≤ 6·(x − 3) + 1 

5x  + 15 + x ≤ 6x - 18 + 1 

6x + 15 ≤ 6x - 17 

6x - 6x ≤ - 17 -15   0x ≤ - 32

Ответ: нет решений.

Система линейных неравенств.

Системой линейных неравенств – называют несколько линейных неравенств, которые должны выполняться одновременно.

Чтобы решить систему неравенств мы должны найти значения переменной, которые подойдут всем неравенствам в системе, т.е. пересечение множеств решений этих неравенств. Пример1.

 

x > 4 x ≤ 7

Решением первого неравенства являются все значения х из интервала (4;∞), а  второго неравенства - значения х из промежутка (−∞;7]. Поэтому решением неравенств системы является пересечение  обоих промежутков, т.е. множество (4;7].

Ответ: (4; 7].

Как вы могли заметить для пересечения решений неравенств в системе удобно использовать числовые оси.

Если в системе находятся требующие преобразований неравенства, то при решении системы каждое неравенство независимо от других преобразовывается к одному из видов: x < c, x > c, x ≤ c, x ≥ c. И только после этого находят общее решение - пересечение решений неравенств на числовой оси.

Пример 2.    

 

 

Решение: 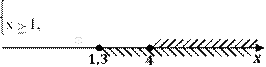 x ≥ 4

Ответ: [4; +∞).

 

Пример 3.   

4(x − 1) < 3x + 1 −3x + 7 ≥ 4(1 − x) Решение: 

4x – 4 < 3x + 1              4x − 3x < 1 + 4            x < 5

−3x + 7≥ 4 − 4x            −3x + 4x ≥ 4 − 7           x ≥ −3

 

 

Ответ: [−3;5)

Системы линейных неравенств и двойные неравенства

 

Помимо рассмотренных выше примеров, есть особый вид систем линейных неравенств: двойные неравенства. Они притворяются, что совсем не системы, но на самом деле ещё какие системы!

 

Например.  Неравенство 3 < x − 1 < 7 можно записать как  систему двух неравенств

x – 1 > 3   x – 1 < 7; неравенство 2x – 5 <  3x + 7  ≤  8x можно записать как 

2x – 5 <  3x + 7 

3x + 7 ≤  8x  

Первое неравенство удобнее решать в виде двойного, из-за того, что в левой и правой части нет переменных. А вот второе лучше решать как систему, т.к. переменные содержатся во всех трех частях неравенства.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Арифметический квадратный корень и его свойства.

Арифметическим квадратным корнем из числа a называется неотрицательное число, квадрат которого равен данному числу a.

Обозначается:  

Читается: квадратный корень из a.

Число a называется подкоренным числом.

4, т. к.4² = 16.

Обратите  внимание!

Квадратный корень из отрицательных чисел не существует.

Например, не имеет смысла, т. к. нет такого действительного числа a, которое в квадрате равно отрицательному числу: a² ≠ −16. 

Чтобы найти квадратный корень из числа, необходимо хорошо знать квадраты чисел.

 

Часто используемые квадраты целых чисел:

 

Значит   и т. д.

Обрати внимание!   

Если подкоренное число — десятичная дробь, то необходимо обращать внимание на количество цифр после запятой:

√0,09 = 0,3, т.к.0,3² =0,3·0,3 = 0,09;  √0,16 = 0,04;  √0,0009 = 0,03.

√0,4 устно вычислить невозможно, т. к. результатом является бесконечная десятичная дробь. 

Если подкоренное число заканчивается нулями, то необходимо обращать внимание на их количество:

;

  устно вычислить невозможно, т. к. результатом является бесконечная десятичная дробь (проверь с помощью калькулятора). 

Если выражение  имеет смысл, то.

В выражениях         16 нерационально сначала извлекать корень из 16, а затем результат возводить в квадрат.

 

Свойства арифметического квадратного корня.

1.

2. 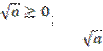                                                                               Выражение  имеет смысл только при , при  выражение  не имеет смысла;

3.                                                                                ;

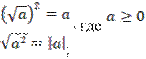4.

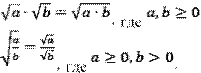5. ;

6.

 

Пример 1. Упростить выражение: √х⁸ Решение.

Степень подкоренного выражения четная, поэтому, во-первых, оно всегда будет неотрицательным и корень всегда будет определен (можем не беспокоиться об ОДЗ):  х⁸ ≥ 0 при всех  х, а, во-вторых, воспользовавшись свойством степени , можем записать: . Используем определение квадратного корня

(не забываем про модуль, т. к. мы пока не знаем, какой знак будет у полученного выражения):   

 

В   роли a тут      выступает х⁴.             При     любых            значениях х выражение       под       модулем неотрицательно, поэтому:

 

Ответ: х⁴.

Основная идея: выделить под корнем квадрат некоторого выражения и воспользоваться свойством корня (эквивалентным определением).

 Пример 2. Упростить выражение:

Решение.

Мы не можем подобрать такое целое число, которое при возведении в квадрат равно  48. Но можем сделать следующее упрощение: представим число 48  так: 48 = 16· 3. Тогда:

 

Воспользуемся тем, что корень из произведения – это произведение корней:

 

Поэтому:

 

Значение  мы можем вычислить: т.к. 4² = 16, то  

Тогда:

 

Или, в таких случаях знак умножения обычно опускают и записывают просто как:

 

Ответ: .

Основная идея: разложить подкоренное выражение на множители так, чтобы один или несколько из них являлись квадратами некоторого выражения:  

Такое упрощение называется вынесение множителя из-под знака корня.

Пример 3. Сравнить значения выражений:  

 

Решение:

Если мы представим    в виде корня из некоторого числа, то сравнить будет легко: где число под корнем больше, там больше и значение. Чтобы это сделать, сначала представим  3  в виде корня: .  Тогда: .

Воспользуемся тем, что произведение корней – корень из произведения:

 

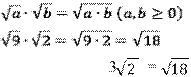        Получаем, что:                     . Поэтому  

Ответ: . 

Основная идея: представить множитель перед корнем в виде квадратного корня из некоторого выражения:

 

Такое преобразование называется внесение множителя под знак корня.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Преобразование выражений, содержащих квадратные корни.

Пример 1. Найти значение выражения √64 ∙ 0,04.

Для нахождения значения выражения, воспользуемся теоремой о корне из произведения:

  

Пример 2. Вычислить значение выражения  .

При вычислении значения выражения необходимо: во-первых, определить, можно ли применить теорему о корне из произведения, то есть можно ли извлечь корень из каждого множителя, если нет, то, во-вторых, следует подкоренное выражение представить в виде произведения множителей, каждый из которых является квадратом целого числа и применить теорему о корне из произведения.

 

Пример 3. Найти значение выражения .

По свойству частного квадратных корней имеем:

  

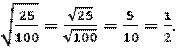
Пример 4. Найти значение выражения.

         Применим тождество:  .

Получим:  

Пример 5. Найти значение выражения . 

Применим тождество  

Получим:  

Пример 6. Упростить выражение .

        Представим степень m¹² в виде (m⁶)²  и воспользуемся тождеством = |x|, получим:

.

Так как m⁶ ≥ 0  при любом m, то |m⁶| = m⁶. Итак,.

Также можно воспользоваться равенством .

Пример:.  Говоря простым языком, если под корнем степень с четным показателем, то при извлечении квадратного корня из этой степени, получаем степень с показателем в 2 раза меньшим.

Пример 7. Вычислить.

Решение.

1  способ:  

Возведем в квадрат каждое число, из полученного уменьшаемого вычтем вычитаемое

 

 

2  способ: 

Воспользуемся формулой сокращенного умножения a² – b² = (a – b)(a + b).

 

Пример 8. Вычислить  , не используя таблицу квадратов чисел и микрокалькулятор. Решение.

Разложим подкоренное число на простые множители:

Значит,

 . 

Получаем,

  

Пример 9. Упростить выражение .

Приведем к наименьшему общему знаменателю дроби, применим формулы сокращенного умножения:

 

 

 

 

 

 

 

 

Формулы корней квадратного уравнения. Решение квадратных уравнений. Уравнения, сводящиеся к квадратным.

 

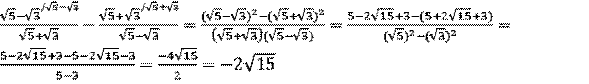
Уравнения вида ax² + bx + c = 0, где a, b, c – некоторые числа называется квадратным,  где  а ≠ 0.

Для решения квадратных уравнений используется такое понятие как дискриминант.

Дискриминантом квадратного уравнения называется число  D= b² - 4ас. Справедливы следующие утверждения:

1. Если D < 0, то уравнение не имеет решений. 2. Если D = 0, то уравнение имеет единственное решение x = − ^𝑏 .

2𝑎

3. Если D > 0, то уравнение имеет два решения:

.

 

Пример 1.

 x² − 2x − 3 = 0  ⇒ a = 1; b = −2; c = −3; D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. 

 

 

Ответ: -1; 3.

Пример 2.

15 − 2x − x² = 0 . –х² – 2х + 15 = 0;  a = −1; b = −2; c = 15; D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. 

 х

Ответ: -5; 1,5

Пример 3. 

x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36; D = 122 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. 

 

х

Ответ: -6.

 

 

 

 

 

Неполное квадратное уравнение.

 

Уравнение ax² + bx + c =0 называется неполным квадратным уравнением, если b =0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю. Если оба коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Если b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

 

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при

                                                                                                           с          

.

a Вывод:

1.      Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство  ^с корней будет два. Формула дана выше;

,

𝑎

2.      Если же (− ^с) < 0 , то корней нет.

𝑎

Если в уравнении с = 0, то уравнение имеет вид  ax² + bx = 0. Такое уравнение имеет два корня.  Достаточно разложить многочлен на множители:

.

 

Биквадратное уравнение.

 

Уравнение вида ax⁴ + bx² + c = 0, где a ≠ 0,  называется биквадратным.

Решение биквадратных уравнений сводится сначала к замене переменной, а потом решению квадратного уравнения: x²  = t, t ≥ 0

 

Получаем квадратное уравнение at² + bt + c = 0, где x и t — переменные, a, b, c - числовые коэффициенты.

Пример 1.

x⁴ − 5x² + 6 = 0

Пусть, x² = t, t ≥ 0, тогда t² − 5t + 6 = 0,

D = b² − 4ac = (−5)² − 4·1·6 = 25 – 24 = 1,

Дискриминант больше нуля, следовательно, два корня, найдем их:

t.

Делаем обратную замену: x²=3 и х² = 2. 

Если x²=3, то  х_;

Если х² = 2, то х.

Ответ: -,

Решение уравнений, сводящихся к квадратным.

Теорема Виета и обратная теорема, обратная теореме Виета.

 

Приведённое квадратное уравнение. Теорема Виета.

 

Квадратное уравнение вида x² + bx + c = 0 называется приведенным, т.к. коэффициент при x² равен 1. Никаких других ограничений на коэффициенты не накладывается. Примеры: x² + 7x + 12 = 0,  x² − 5x + 6 = 0 — это приведенные квадратные уравнения.

 

Теорема Виета.

Рассмотрим приведенное квадратное уравнение вида x² + px + q = 0. 

Если приведённое квадратное уравнение имеет действительные корни x1 и x2,  то верны следующие утверждения:

1.      x1 + x2 = −p, т.е. сумма корней приведенного квадратного уравнения равна коэффициенту при переменной x, взятому с противоположным знаком;

2.      x1 · x2 = q,  т.е. произведение корней квадратного уравнения равно свободному коэффициенту.

 

Теорема, обратная теореме Виета.

 

Если x₁ + x₂ = −p, а x₁ · x₂ = q, то х₁ и х₂ – корни приведённого уравнения x² + px + q = 0.

Пример 1. 

Используя теорему, обратную теореме Виета, найти корни уравнения x² − 9x + 20 = 0. Решение:

x₁ + x₂ = −p    x₁ = 4, x₁ · x₂ = q       x₂ = 5.

Ответ: 4; 5.

Пример 2. Составить квадратное уравнение по его корням: x1 = -3,    x2 = 6.

Решение: 

Так как  x₁ = -3,  x₂ = 6  корни уравнения  x² + px + q = 0, то по теореме, обратной теореме Виета, составим уравнения: p = - (x₁ + x₂) = - (-3 + 6) = -3; q = x₁ · x₂ = -3 · 6 = -18. Следовательно, искомое уравнение: x² - 3x - 18 = 0.

Ответ:  x² - 3x - 18 = 0.

Пример 3. Не решая уравнение x² - 3x – 4 = 0, вычислите значение выражения  x1²+x2².

Решение. 

По теореме Виета сумма корней этого приведенного квадратного уравнения x1 + x2 = -p = 3, а произведение x₁ ∙ x₂ = q = -4.

Выражение x1² + x2²  получится, если возвести в квадрат обе части равенства x1 + x2 = -p; (x₁ + x₂)² = (-p)²;  раскрываем скобки: x₁² + 2x₁x₂ +  x₂² = p²;  выражаем искомую сумму:  x₁² + x₂² = p² - 2x₁x₂ = p²- 2q. Мы получили полезное равенство: x₁² + x₂² = p² - 2q. Поэтому x₁² + x₂² = 3² - 2· (-4) = 9 + 8 = 17.

Ответ: 17.

 

Решение уравнений, сводящихся к квадратным.

 

Пример 4. Решить уравнение (х + 7)⁴ – (х + 7)²  - 2 = 0.

Решение. Обозначим (х + 7)² = t, t ≥ 0, тогда уравнение принимает вид: t² – t – 2 = 0. t₁ + t₂ = 1   t₁ = -1 – не удовлетворяет условию t ≥ 0, t_{1 ·} t₂ = -2    t₂ = 2.

(х + 7)² = 2

х.

Ответ: -.

 

Дробно-рациональные уравнения.

Рациональные уравнения,  которые можно свести к дроби  ^𝑃(𝑥) = 0 называется дробно-

𝑄(𝑥)

рациональным уравнением, где P(x) и Q(x) – многочлены.

𝑃(𝑥)

Выражение   имеет смысл только в том случае, если выполняется условие Q(x) ≠ 0.

𝑄(𝑥)

Значит, рациональное уравнение имеет решение при условии P(x) = 0, Q(x) ≠ 0.

Пример 1. Решить уравнение    

Решение. Выполним тождественные преобразования уравнения.

1)  Перенесем все слагаемые из правой части уравнения в левую:

    

2)  Преобразуем левую часть уравнения к рациональной дроби:

 

3)  Применим условие равенства дроби нулю:

 

Ответ: 5.

Чтобы решить дробно-рациональное уравнение, нужно:

1.      Перенести все слагаемые из правой части уравнения в левую.

2.      Преобразовать левую часть уравнения к рациональной дроби.

3.      Применить условие равенства дроби нулю.

4.      Записать ответ.

Пример 2. Решите уравнение  

Решение:

  

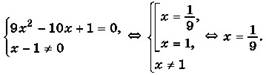
 Ответ: .

Пример 3. Решите уравнение  

Решение:

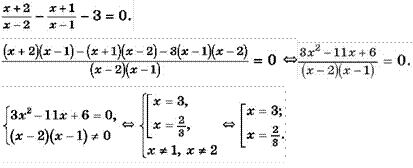
Ответ: ; 3.

Пример 4. Решите уравнение  

Решение:

  

  

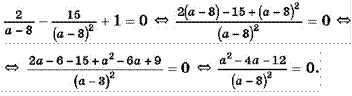
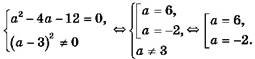
 Ответ: -2; 6.

 

Пример 5. Решите уравнение   

Решение:

Выполним замену переменной

  

и получим уравнение

  

которое  является дробно-рациональным. Решим его, применив алгоритм:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение систем уравнений второй степени.

Системой уравнений второй степени с двумя переменными называются такие системы уравнений с двумя переменными, что хотя бы одно из этих уравнений – уравнение второй степени, а второе – не выше второй степени.

Решением системы называется такой набор значений переменных,  при котором каждое уравнение системы обращается в верное равенство.

Решить систему уравнений – значит найти все её решения или доказать, что их нет.

 

Метод подстановки.

1)  Из оного уравнения выражается  одна переменная через другую;

2)  Полученное выражение подставляется во  второе уравнение, 

3)  Решается получившееся уравнение с одной переменной;

4)  Полученное значение переменной подставляется в выражение из пункта 1);

4) Решая уравнение, полученное после подстановки в выражение из пункта 1), находят соответствующие значения второй переменной.

 

Пример 1. Решим систему уравнений

 

Выразим из второго уравнения переменную х через у: х = 1 - 2у. Подставим в первое уравнение вместо х выражение 1 - 2у, получим уравнение с переменной у:

(1 - 2у)² - 3(1 - 2у)у - 2у² = 2.

После упрощения получим равносильное уравнение: 8у² - 7у - 1 = 0.

  

Соответствующие значения х можно найти, подставив найденные значения у в одно из уравнений системы, например во второе уравнение. Удобнее, однако, воспользоваться формулой х = 1 - 2у.

Подставив в выражение х = 1 - 2у значение y1 = -   ,  получим x1 = 1/ Подставив в формулу х = 1 - 2у значение у2 = 1, получим x2 = -1.

Ответ: (1  ; − ) , (−1; 1).

Пример 2. Решим систему уравнений

 

Воспользовавшись тем, что х ≠ 0, выразим из второго уравнения переменную у через х:

6

𝑦 =  и подставим в первое уравнение вместо y. Получим уравнение  

x

В результате решения получим корни  х1 = -3, х2 = 3. Если х₁ = -3, то y₁ = ⁶ = -2; если х₂ = 3, y₂ = 2.  Ответ: (-3; -2), (3; 2). 

−3

 

Метод алгебраического сложения.

Пример 3. Решить систему способом алгебраического сложения:

 

Домножим первое уравнение системы на число, противоположное коэффициенту при переменной y во втором уравнении. В данном случае:

 

Выполним покомпонентное сложение двух уравнений:

 

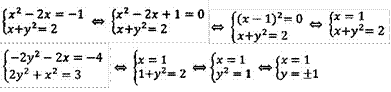
Ответ: (1; 1) и (1; -1).

Метод введения новой переменной.

Пример 4. Решить систему уравнений способом введения новой переменной:

 

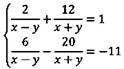
Введем новую переменную:

 

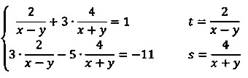
Решим данную систему:

 

 

Теперь выполним обратную подстановку:

 

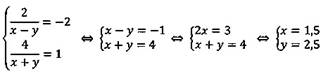
Ответ:  (1,5; 2,5).

 

 

Пример 5. Решить  систему  уравнений:

х² у² ху 32,



ху 2(ху)  26.     

 Решение. 

 Пусть х + у = u,  ху = v, тогда  х² + у² =( х + у)² - 2ху = u² - 2v  и система  примет  вид:

u² 2vu32



           v2u26            

Решим  полученную  систему  методом  подстановки. Выразим  из второго  уравнения v  через  u: v = 26 – 2u и подставим в первое уравнение: 

u² – 2(26 – 2u) + u = 32 u² +5u – 52 – 32 = 0 u² +5u – 84 =0 u₁ = 7, u₂ = -12.

Если u₁ = 7, то v₁ = 26 – 2 · 7 = 12=>          х + у = 7

 =>    ху = 12 => x₁ = 3,  y₁ = 4 или x₁ =4, y₁ = 3.

Если u₂ = -12, то v₂ = 50 =>     х + у = -12

 =>    ху = 50 => система не имеет решений. Ответ: (3;4), (4;3).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Квадратичная функция. Построение графиков квадратичной функции.

 

Функция вида  y = ax² + bx + c,  где  a, b, c  — реальные числа,  a ≠ 0, называется квадратичной функцией.

Графиком квадратичной функции является парабола. Область определения функции  D(y) = (-∞; +∞).

 

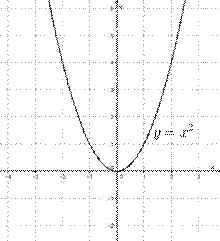
Функция y = x² (a = 1, b = c = 0).

Составим таблицу значений и построим график функции

x	-2	-1	0	1	2
y = x2	4	1	0	1	4

 

D(y) = (-∞; +∞);

 

E(y) = [0;+∞), так как x² ≥ 0 при любом действительном значении x;

 

Функция  y = x²  убывает при x ∈ (-∞; 0] и возрастает при x ∈ (0; +∞).

 

Рис.1 

 

График  функции y = -x² имеет вид:

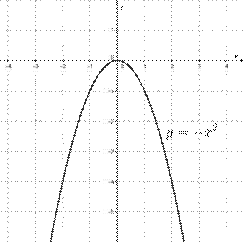Рис.2  Для нахождения координат базовых точек составим таблицу:

x	-2	-1	0	1	2
y = -x2	-4	-1	0	-1	-4

 

График функции y = -x² симметричен графику функции y = x² относительно оси Оx. Наименьшее значение функции y = x² равно 0 при x = 0.

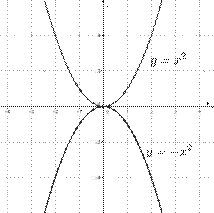Рис.3

Точка пересечения параболы с её осью симметрии называется вершиной параболы.

 

 

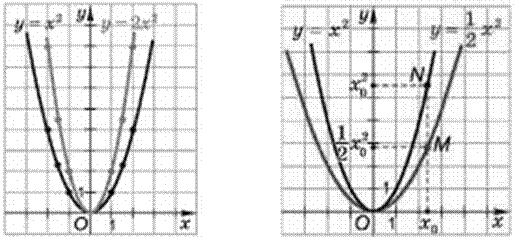
Функция y = ax²  (b = c = 0)  и её график

 y = 2x2                                                                                  y = ^𝟏x2  

𝟐

                

 

 

 

 

 

 

 

 

 

 

 

 

 

D(y) = (-∞; +∞)

1) a > 0

E(y) = [0;+∞),так как x² ≥ 0 при любом x ∈ D(y). График функции y=ax²  получается из графика y = x² сжатием к оси Ох, если 0 < a < 1, или растяжением, если а > 1.

Функция y = ax²  убывает при x ∈ (-∞; 0] и возрастает при x ∈ (0; +∞).

Наименьшее значение функции у(0) = 0 достигается в вершине параболы – точке с координатами (0;0).

При а > 0 ветви параболы направлены вверх, ось Оу является осью симметрии параболы.

2) a < 0

E(y) = (−∞; 0). График функции y = ax²  получается из графика y =|а|x²  осевой симметрией относительно оси Ох (см. рис. 3).

Функция y = ax²  возрастает при x ∈ (-∞; 0] и убывает при x ∈ (0; +∞). При  a < 0 ветви параболы направлены вниз. 

 

График функции y = ax² + bx + c

 

Графиком любой квадратичной функции y = ax² + bx + c, где a ≠ 0, является парабола с вершиной в некоторой точке с координатами (х0; у0) и осью симметрии, проходящей через точку х0 параллельно оси Оу.

Рассмотрим для примера две квадратичные функции.

Пример 1.  Построить график функции y = x²−2x−1 (рис. 1).

Пример 2. Построить график функции y = −2x²+4x (рис. 2).

         Область значений функции E(y) считывается с графика, она зависит от координаты y, вершины параболы и направления ветвей параболы.            Пример 1. E(у) = [−2;+∞); так как  a > 0, то ветви направлены вверх (см. рис. 1);  параметр c указывает, в какой точке парабола пересекает ось Oy.

 

x	2	3	4
y	−1	2	7

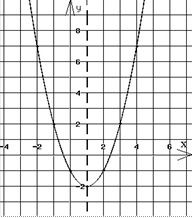         x₀ = - ^𝑏 =2:2=1;  y₀=1²−2·1−1=−2.                                     

 Ветви параболы направлены вверх, т. к.2𝑎                         а = 1 > 0.     

 Парабола пересекает ось Oy в точке (0;−1). 

  

Симметрично строим левую сторону параболы 

 

 

                                                                                                                                   Рис. 1. График²−2x −1функции               

y=x

 

Чтобы построить график квадратичной функции, необходимо:

1)  вычислить координаты вершины параболы: x0 = - ^𝑏 и y0 — которую находят, подставив

2𝑎

значение x0  в формулу функции;

2)  отметить вершину параболы на координатной плоскости, провести ось симметрии параболы;

3)  определить направление ветвей параболы;

4)  отметить точку пересечения параболы с осью Oy;

5)  составить таблицу значений, выбрав необходимые значения аргумента x.

Решив квадратное уравнение ax²+bx+c=0, получаем точки пересечения параболы с осью Ox, или корни функции (если дискриминант D>0); если D<0, то точек пересечения параболы с осью Ox не существует; если D=0, то вершина параболы находится на оси Ox.

Но не всегда точки пересечения с осью Ox являются рациональными числами; если невозможно точно вычислить корень из D, то такие точки не используют для построения графика.

 

Пример 2.   E(у) = (−∞;2];  так как  a < 0, то ветви направлены вниз (см. рис. 2).

  

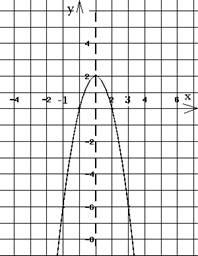В данном случае легко вычислить корни:

−2x²+4x=0; x(−2x+4)=0; x=0, или −2x+4=0;  x=2;  x₁=0;x₂=2.

Координаты вершины параболы: x      1;

                    2𝑎                        2∙(−2)

y₀= −2⋅12 + 4⋅1 = 2.

 

В таблице достаточно одного значения:

если x=3, то y = −2⋅(3)² + 4⋅3 = −18 + 12 = −6.

  

        Симметрично, если x = −1, то y = −6                           Рис. 2. График  функции y=−2x2+4x

Квадратные неравенства

 

 Квадратное неравенство – это неравенство вида ax²+ bx + c < 0 (вместо знака < может быть любой другой знак неравенства ≤, >, ≥), где a, b и c – некоторые числа, причем a ≠ 0, а x – переменная (переменная может быть обозначена и любой другой буквой).

Графический способ решения квадратных неравенств

Графический способ решения квадратных неравенств ax²+ bx + c < 0  (≤, >, ≥) заключается в анализе графика квадратичной функции y = ax²+ bx + c для нахождения промежутков, в которых указанная функция принимает отрицательные, положительные, неположительные или неотрицательные значения. Эти промежутки и составляют решения квадратных неравенств ax²+ bx + c < 0, ax²+ bx + c > 0, ax²+ bx + c ≤ 0 и ax²+ bx + c ≥ 0  соответственно.

Пример 1. Решить неравенство: x² + 2x - 48 < 0.

Решение. Введем функцию y = x² + 2x - 48.

Графиком этой функции является парабола, ветви которой направлены вверх, так как a =

1.

Выясним, как расположен график этой функции относительно оси x. Для этого решим квадратное уравнение x² + 2x - 48 = 0. Это уравнение имеет два корня: x₁ = -8 и x₂ = 6.

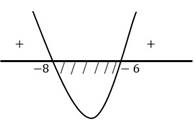Значит, парабола  y = x² + 2x - 48 пересекает ось x в двух точках, абсциссы которых равны -8 и 6. Схематично изобразим эту параболу.

 

 

 

 

Ответ: x ϵ (−8; 6)

Пример 2. Решить неравенство  – x² + 2x + 15 < 0.

Решение. График функции y = -x² + 2x + 15 – это парабола, ветви которой направлены вниз, так как a < 0.

Выясним, как расположен график функции y = -x² + 2x + 15 в координатной плоскости, пересекает ли он ось x и в каких точках. Для этого решим уравнение:

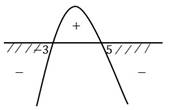-x² + 2x + 15 = 0 x₁=-3; x₂=5

Схематично изобразим эту параболу

 

Функция принимает отрицательные значения при x принадлежит (-∞; -3) или (5; +∞).

Ответ: x 𝜖 (-∞; -3) ∪ (5; +∞).

Решение квадратных неравенств методом интервалов

Суть метода интервалов, по отношению к решению квадратных неравенств  ax²+ bx + c < 0 (≤, >, ≥), состоит в определении знаков, которые имеют значения квадратного трехчлена ax²+ bx + c на промежутках, на которые разбивается координатная ось нулями этого трехчлена (при их наличии). Промежутки со знаками минус составляют решения квадратного неравенства ax² + bx + c < 0, со знаками плюс – неравенства ax²+ bx + c > 0, а при решении нестрогих неравенств к указанным промежуткам добавляются точки, отвечающие нулям трехчлена. 

Для примера возьмем трехчлен x² + 4x − 5. Корни этого трехчлена 1 и − 5  разбивают координатную ось на три промежутка (−∞, −5),  (−5, 1) и  (1, +∞). Начнем с промежутка (1, +∞). Для того, чтобы упростить себе задачу, примем х = 2. Получаем 2² + 4 ⋅ 2 − 5 = 7,  7  – положительное число. Это значит, что значения данного квадратного трехчлена на интервале  (1, +∞) положительные и его можно обозначить знаком «+». Для определения знака промежутка (−5, 1) примем  x = 0. Имеем  0² + 4 ⋅ 0 − 5 = − 5. Ставим над интервалом знак «−». Для промежутка  (−∞, −5) возьмем  x = − 6, получаем  (−6)² + 4·(−6) − 5 =

        7. Отмечаем                        этот                       интервал                       знаком                       «+».

         Намного быстрее определить знаки можно с учетом следующих фактов: если дискриминант положительный, то квадратный трехчлен с двумя корнями дает чередование знаков его значений на промежутках, на которые разбивается числовая ось корнями этого трехчлена. Это значит, что нам вовсе не обязательно определять знаки для каждого из интервалов. Достаточно провести вычисления для одного и проставить знаки для остальных, учитывая принцип чередования. При желании, можно и вовсе обойтись без вычислений, сделав выводы о знаках по значению старшего коэффициента. Если a > 0, то мы получаем последовательность знаков «+,  −,  +»,  а если  a < 0 – то «−,  +,  −». У квадратных трехчленов с одним корнем, когда дискриминант равен нулю, мы получаем два промежутка на координатной оси с одинаковыми знаками. Это значит, что мы определяем знак для одного из промежутков и для второго ставим такой же. Здесь также применим метод определения знака на основе значения коэффициента a a: если  a > 0, то будет « +, + », а если  a < 0, то   «  −, − ».  Если квадратный трехчлен не имеет корней, то знаки его значений для всей координатной прямой совпадают как со знаком старшего коэффициента  a, так и со знаком свободного члена  c.

Пример 1.  Решить неравенство 2х² + 5х – 3 >0.

Найдем корни уравнения 2х² + 5х – 3 =0 и получим х1 = -3 и х2 = 0,5. Нанесем точки х1 = -3 и х2 = 0,5 на числовую ось. Эти точки разбивают ось на три интервала (промежутка). Определим знак многочлена 2х² + 5х – 3 в любом промежутке, например в среднем. Подставим любую точку этого промежутка (не совпадающую с его концами), например х  = 0 в выражение 2х² + 5х – 3 и получим 0+0-3 = -3 < 0.  

Таким образом, в точках среднего интервала выражение 2х² + 5х – 3 отрицательно. 

 

Расставляем знаки на остальных интервалах в порядке чередования. Выписываем те промежутки, на которых стоит знак «+» и получаем решение неравенства 2х² + 5х – 3 >0;  х < -3;  х > 0,5.  Ответ: х < -3;  х > 0,5.

 

Пример 2. Решить неравенство х² - 4х + 3 < 0. По теореме Виета:

х₁ + х₂ = 4,  х₁ · х₂ = 3,  х₁ = 1, х₂ = 3.

Нанесем точки х1 = 1 и х2 = 3 на числовую ось. Эти точки разбивают ось на три интервала (промежутка).

 

Выписываем те промежутки, на которых стоит знак «-» и получаем решение неравенства х² - 4х + 3 < 0;   1< х < 3. Ответ: 1< х < 3.

 

Пример 3. 𝒙𝟐𝟐−𝟏𝟎𝒙+𝟐𝟓 ≤ 𝟎

𝒙 −𝟑𝒙−𝟏𝟖

Приравниваем к нулю левую часть. Получаем:

   

Поскольку в ходе решения уравнения x² - 10x + 25 = 0 получили дискриминант, равный нулю, в соответствующей точке x = 5  — «петля». Отмечаем полученные точки на числовой прямой:

 

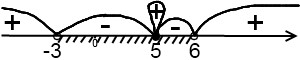
Знак неравенства — меньше либо равно, поэтому выбираем промежутки со знаком « - ». Точка х = 5 — закрашенная, поэтому ее включаем в ответ (то есть разрывать промежуток от -3 до 6 не нужно). Ответ: х∈ (-3;6).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список литературы

 

1.      Виленкин Н.Я. и др. Алгебра 8 (учебное пособие для учащихся 8 класса), Москва, 2009

2.      Галицкий М.Л. и др. Сборник Задач по алгебре 8-9; Москва, 2006

3.      Шестакова С.А. и др. Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы, 9 класс; Москва, 2007

4.      Аверьянов Д.И., Алтынов и др. Большой справочник для школьников; Москва. 1998

5.      Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре 8 класс; Москва, 2002

6.      Интернет-ресурсы:  http://fizmat.by/math/inequality/square_inequality https://zaochnik.com/ https://www.uznateshe.ru/ https://100ballov.kz/

https://ik-ptz.ru/social-studies/