Совместные действия над алгебраическими дробями

Конспект урока

Тема урока: Совместные действия над алгебраическими дробями.

Тип урока: Урок обобщения и систематизации знаний.

Учебная задача урока: обобщить и систематизировать знания и умения учащихся по действиям с алгебраическими дробями.

Диагностируемые цели урока:

В результате урока ученик

знает:

- определение алгебраической дроби

- формулировки правил выполнения различных действий над алгебраическими дробями

- виды задач, решаемых на основе изученной теории

умеет: 

- выполнять различные виды заданий на различные действия над алгебраическими дробями

понимает:

- взаимосвязь между дидактическими единицами темы

Учебные действия, формируемые на уроке:

• Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом должна осуществляться осмысленная организация собственной деятельности ученика.
• Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что ещё неизвестно, планирование - определение последовательности промежуточных целей с учётом конечного результата, оценка - выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения, волевая саморегуляция как способность к мобилизации сил и энергии,  способность к волевому усилию к выбору в ситуации мотивационного конфликта и  к преодолению препятствий.
• Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т. е. определение цели сотрудничества, функций участников, способов взаимодействияспособов взаимодействия, в том числе совершенствование навыков работы в группе, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и  условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение.
• Познавательные: анализ объектов  с целью выделения признаков (существенных, несущественных); построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей,структурирование знаний,выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.

Методы обучения: эвристическая беседа, репродуктивный, частично-поисковые, УДЕ.

Форма работы: фронтальная, парная, групповая.

Средства обучения: традиционные, презентация, карточки с заданиями, канва-таблица.

Структура урока:

I.                   Мотивационно-ориентировочная часть (10 минут).

1.1.          Актуализация полученных знаний.

1.2.          Мотивация.

1.3.          Постановка учебной задачи (цели) урока.

II.                Операционно-познавательная часть (33 минуты).

2.1. Обобщение и систематизация знаний о совместных действиях с алгебраическими дробями

III.             Рефлексивно-оценочная часть (2 минуты).

3.1. Подведение итогов урока.

 

Ход урока

I. Мотивационно-ориентировочная часть

1.1. Актуализация полученных знаний.

Работа фронтальная со всем классом с записями в тетради.

- Выберите из предложенных выражений алгебраические дроби

А)

Б)

В)

Г)

(Ответ: А, В)

- Что называется алгебраической дробью?

(Алгебраической дробью называется выражение вида , где P и Q – многочлены, P – числитель алгебраической дроби, Q – знаменатель алгебраической дроби, Q¹0)

Работа в парах (5 мин)

1 ученик

Выполнить действия:

1)  

2)  

3)   

(Решение: 1) =

2)

3) )

2 ученик

1)

2)

3)

(Решение: 1)

2)

3))

Сдают заполненные карточки с решениями

Проверка правильности решения по слайду презентации

- Какие правила вы использовали при решении заданий?

(Алгоритм сложения (вычитания) алгебраических дробей с разными знаменателями:

Чтобы сложить (вычесть) алгебраические дроби, нужно:

1.Привести  дроби к общему знаменателю;

2.Выполнить сложение (вычитание) полученных дробей с одинаковыми знаменателями, т.е. сложить (вычесть) их числители, а знаменатель оставить без изменений.

Алгоритм приведения алгебраических дробей к общему знаменателю:

Чтобы привести алгебраические дроби к наименьшему общему знаменателю, нужно:

1. Найти наименьший общий знаменатель дробей.

2. Найти дополнительные множители для каждой дроби, разделив наименьший общий знаменатель дробей на знаменатель дроби.

3.Числитель и знаменатель каждой дроби умножить на её дополнительный множитель

Правило умножения алгебраических дробей:

Чтобы умножить одну алгебраическую дробь на другую, надо:  

1.     перемножить их числители и результат записать в числитель, 

2.     перемножить их знаменатели и результат записать в знаменатель

Правило деления алгебраических дробей:

Чтобы выполнить деление алгебраических дробей, надо первую дробь умножить на дробь, обратную второй)

1. 2. Мотивация

-Итак, в главе «Алгебраические дроби» вы изучили определение алгебраической дроби и различные правила выполнения действий над алгебраическими дробями. На следующем уроке вы пишите контрольную работу по данной теме.

1.3. Постановка учебной задачи (цели) урока.

- Поэтому, целью сегодняшнего урока будет проведение обобщения и систематизации изученного вами материала по теме «Совместные действия над алгебраическими дробями».

II. Операционно-познавательная часть.

Тема урока «Совместные действия над алгебраическими дробями» (у учителя она появляется на презентации, ученики записывают в тетрадь)

- Итак, вспомним основной теоретический материал по теме, заполняя канву-таблицу

Незаполненная канва-таблица

Определение: Алгебраической дробью называется                      , где

Основное свойство дроби Если                                    алгебраической дроби на один и тот же многочлен, то получится             ей алгебраическая дробь.

Приведение алгебраических дробей к общему знаменателю Чтобы привести алгебраические дроби к наименьшему общему знаменателю, нужно: 1. Найти                                                             дробей. 2. Найти                            для каждой дроби,    3.Числитель и знаменатель каждой дроби               на её

Действия с алгебраическим дробями

- сложение (вычитание) алгебраических дробей с одинаковыми знаменателями Чтобы сложить (вычесть) алгебраические дроби с одинаковыми знаменателями, нужно сложить (вычесть)                       , а               без изменений.

- сложение (вычитание) алгебраических дробей с разными знаменателями Чтобы сложить (вычесть) алгебраические дроби с разными знаменателями, нужно: 1. Привести  дроби к 2.Выполнить                            полученных дробей с

- умножение алгебраических дробей Чтобы умножить одну алгебраическую дробь на другую, надо:   1.      перемножить их             и результат записать в  2.      перемножить их                 и результат записать в

- деление алгебраических дробей Чтобы выполнить деление алгебраических дробей, надо  умножить на дробь,

 

 

 

 

Заполненная канва-таблица

Определение: Алгебраической дробью называется выражение вида , где P и Q – многочлены, P – числитель алгебраической дроби, Q – знаменатель алгебраической дроби, Q¹0

Основное свойство дроби Если числитель и знаменатель алгебраической дроби умножить или разделить на один и тот же ненулевой многочлен, то получится равная ей алгебраическая дробь.

Приведение алгебраических дробей к общему знаменателю Чтобы привести алгебраические дроби к наименьшему общему знаменателю, нужно: 1. Найти наименьший общий знаменатель дробей. 2. Найти дополнительные множители для каждой дроби, разделив наименьший общий знаменатель дробей на знаменатель дроби. 3.Числитель и знаменатель каждой дроби умножить на её дополнительный множитель

Действия с алгебраическим дробями

- сложение (вычитание) алгебраических дробей с одинаковыми знаменателями Чтобы сложить (вычесть) алгебраические дроби с одинаковыми знаменателями, нужно сложить (вычесть) их числители, а знаменатель оставить без изменений.

- сложение (вычитание) алгебраических дробей с разными знаменателями Чтобы сложить (вычесть) алгебраические дроби с разными знаменателями, нужно: 1.Привести  дроби к общему знаменателю; 2.Выполнить сложение (вычитание) полученных дробей с одинаковыми знаменателями.

- умножение алгебраических дробей Чтобы умножить одну алгебраическую дробь на другую, надо:   1.перемножить их числители и результат записать в числитель,  2.перемножить их знаменатели и результат записать в знаменатель

- деление алгебраических дробей Чтобы выполнить деление алгебраических дробей, надо первую дробь умножить на дробь, обратную второй.

 

(Учитель вызывает одного ученика к доске, остальные решают в тетради)

Упр. 1. Найдите допустимые значения букв, входящих в дробь

а)

б)

в)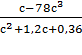

(Решение: Допустимыми значениями значения букв, входящих в дробь, называют те значения, при которых знаменатель дроби не обращается в 0.

а) для дроби  допустимыми значениями значения букв, входящих в дробь, будут все значения a и b, кроме а+2=0, a=-2, т.е. ответ: а≠-2

б) для дроби  допустимыми значениями значения букв, входящих в дробь, будут все значения a, кроме =0, a=0 и a=1, т.е. ответ: a¹0, a¹1.

в) для дроби 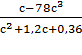 допустимыми значениями значения букв, входящих в дробь, будут все значения c, кроме . Решим это уравнение: ,

В левой части уравнения мы можем выражение свернуть по формуле квадрат суммы -  и получим - , т.е. ответ: c¹-0,6).

Упр.2. Сократите дробь:

А)

Б)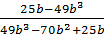

(Решение: А)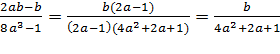

Б))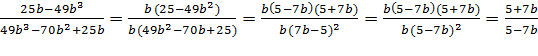

Упр. 3. Упростите выражение

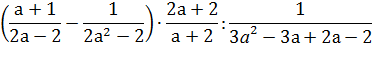
-Прежде чем начать выполнять упражнение, что мы должны сначала сделать?

(расставить порядок действий)

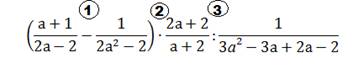
1)

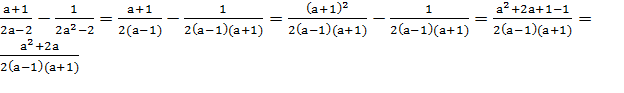
2)

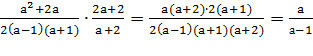
3))

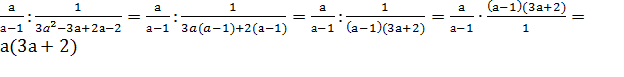Упр. 4. Найдите значение выражения:

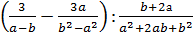при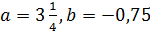

(Решение:

Упростим выражение перед тем как подставить данные значения букв:

1)

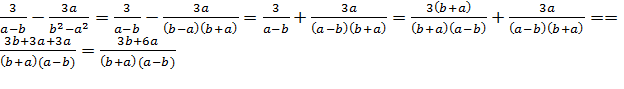
2)

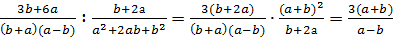
Подставим 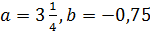в полученное выражение:.

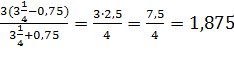Работа по группам

Примерные задания для групп

Упр. 1. Найдите допустимые значения букв, входящих в дробь

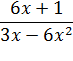
(Решение: для дроби  допустимыми значениями значения букв, входящих в дробь, будут все значения x, кроме , 3x(1-2x)=0, x=0, x= т.е. ответ: x¹0, x¹).

Упр.2. Сократите дробь:

А)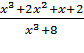

Б)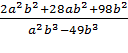

(Решение: А)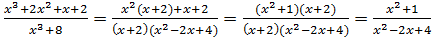

Б))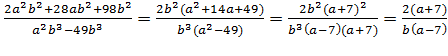

№ 3. Упростите выражение: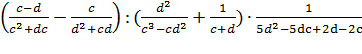

(Решение: 1)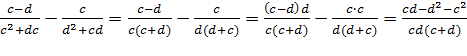

2)

3)

4))

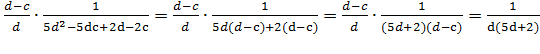№ 4. Найдите значение выражения: 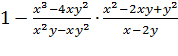при

(Решение: Упростим выражение перед тем как подставить данные значения: 1)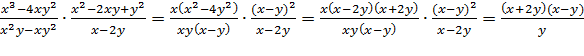

2)

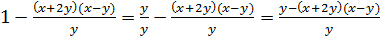
Подставим  в полученное выражение: .)

III. Рефлексивно-оценочная часть.

- Какова была цель урока? (проведение обобщения и систематизации изученного материала по теме «Совместные действия над алгебраическими дробями»)

- Достигли ли мы цель? (Да)

- Как мы её достигли? Какие виды задач решали? (Повторили определение алгебраической дроби, правила выполнения различных действий над алгебраическими дробями, решали задачи на нахождение допустимых значений букв, входящих в дробь, сокращение алгебраических дробей, на упрощение выражений, на нахождение значения выражения)

Домашнее задание:

№ № 502(2,4), 503(2), 504, 512(2)

 

Скачано с www.znanio.ru