СТОЛБЧАТЫЕ И КРУГОВЫЕ ДИАГРАММЫ

Интервальные ряды

Цели: ввести понятия интервального ряда, характеристик выборочного исследования; формировать умения использовать данные понятия при решении задач.

Ход урока

I. Организационный момент.

II. Устная работа.

Для упорядоченных рядов найдите размах, среднее арифметическое, моду и медиану:

а) 0; 0; 1; 2; 3;

б) 1; 2; 2; 2; 3; 3;

в) 1; 2; 3; 4; 5; 5.

III. Проверочная работа.

В а р и а н т  1

1. В таблице приведён возраст сотрудников одного из отделов:

Найдите размах, моду, медиану и среднее арифметическое этого ряда.

2*. Постройте ряд из четырёх чисел, у которого размах равен 2, а среднее арифметическое равно моде.

В а р и а н т  2

1. В таблице приведены количество очков, набранных в чемпионате некоторыми стрелками:

Найдите размах, моду, медиану и среднее арифметическое этого ряда.

2*. Постройте ряд из четырёх чисел, у которого размах равен 2, а среднее арифметическое равно медиане.

IV. Проверка домашнего задания.

№ 1034.

Р е ш е н и е

Среднее арифметическое находим по формуле:

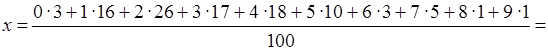
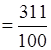 = 3,11.

Среднее арифметическое характеризует уровень наблюдаемых значений, а при известном п = 100 позволяет сразу определить общее число сорных семян во всех пакетах:

3,11 · 100 = 311.

Мода М = 2 показывает, что больше всего пакетов, в которых содержится по 2 семени сорняка.

О т в е т: 3,11; 2.

V. Объяснение нового материала.

Объяснение проводить согласно пункту учебника.

1. Запись статистической информации в форме простого ряда имеет два наиболее существенных недостатка: громоздкость и труднообозримость (закономерности ряда не бросаются в глаза). В этих случаях для анализа данных строят интервальный ряд. Для этого разность между наибольшим  и  наименьшим  значениями  делят  на  несколько  равных  частей (примерно 5–10) и, округляя полученный результат, определяют длину интервала. За начало первого интервала часто выбирают наименьшее данное или ближайшее к нему целое число, его не превосходящее. Для каждого интервала указывают число данных, попадающих в этот интервал, или выраженное в процентах отношение этого числа к общей численности данных. При этом граничное число обычно считают относящимся к последующему интервалу.

Рассмотреть пример со с. 217 учебника.

2. Вводится понятие выборочного исследования и выборочной совокупности (выборки), которая подвергается исследованию.

Репрезентативность выборки рассматривается на примере со с. 218 учебника.

VI. Формирование умений и навыков.

1. № 1035.

Р е ш е н и е

Для построения интервального ряда находим наименьшее и наибольшее значение результатов наблюдения:

х_min  = 15, х_max = 39.

Определяем количество частичных интервалов:

.

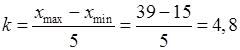Мы увеличим х_max = 39 до х'_max = 40, чтобы получить целое k. Так можно сделать, поскольку при этом мы не теряем ни одного наблюдавшееся значение и не допускаем никаких посторонних значений в результаты.

.

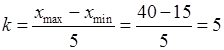Строим таблицу распределения интервального ряда.

Поскольку х_min  = 15 мин попало на границу первого интервала, и мы включили это значение в интервал, то и во всех случаях попадания значений  на  границу  интервалов  будем  включать  эти  значения  в  правый интервал.

2. В таблице показано распределение призывников района по росту:

По данным таблицы составьте новую таблицу с интервалом в 10 см.

Р е ш е н и е

В таблице весь размах значений наблюдаемой величины (от 155 до 195 см) разбит на k = 8 частичных интервалов шириной h = 5 см. Объединим каждые два соседних интервала, начиная с первого, и просуммируем частоты соседних интервалов; получаем новую таблицу распределения с интервалом h₁ = 10 см и числом интервалов k = 4:

3. Имеются следующие данные о распределении участников похода по возрасту:

Заменив каждый интервал его серединой, найдите средний возраст участников похода.

Р е ш е н и е

Середины интервалов имеют значения 20, 24, 28, 32 (лет).

Объём выборки п = 25 + 18 + 5 + 2 = 50.

Средний возраст участников похода:

Т_ср = 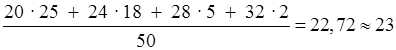 года.

Полученное значение является приблизительным, так как вместо реальных наблюдавшихся значений мы осредняли середины интервалов ряда распределения.

О т в е т: ≈23 года.

4. № 1037.

Р е ш е н и е

а) Не является, так как примерно половина восьмиклассников – мальчики, у них есть свои особенности, а их не опрашивали.

б) Не является, так как время на выполнение уроков зависит от расписания, которое меняется по дням недели. В четверг готовят уроки на пятницу, а в пятницу могут быть уроки, не требующие большой подготовки.

в) Не является, так как гимназии и лицеи – это меньшая часть общеобразовательных учреждений со специальным отбором учащихся и специфическими особенностями учебных программ и перечня изучаемых предметов. Время на выполнение уроков в гимназиях и лицеях может отличаться от времени, затрачиваемого учениками обычных школ.

О т в е т: а) нет; б) нет; в) нет.

VII. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– В каком случае таблица частот не является удобной для анализа статистических данных?

– Что из себя представляет интервальный ряд?

– Чем выборочное исследование отличается от сплошного?

– В каком случае выборка является репрезентативной? Приведите примеры.

Домашнее задание: № 1036, № 1038, № 1097.

Скачано с www.znanio.ru