Управление образования Администрации городского округа город Уфа Республики Башкортостан

МАОУ ДО «Научно-информационно-методический центр» 

Городской фестиваль науки 

 «Познаем. Исследуем. Проектируем»

 

 

Направление: «Инновации в нашей жизни»

 

 

Тема научно–исследовательской работы (проекта)

Тайна последней цифры степени

 

 

Омелина Виолетта Артемовна

учащегося  6Е  класса

Муниципальное автономное  общеобразовательное учреждение 

«Центр образования№ 51  имени В.М.Паращенко»   городского округа 

г. Уфа РБ 

 

Научный руководитель:

 Егорова Нурия Талгатовна, 

Учитель математики, МАОУ

«Центр образования№ 51  имени В.М.Паращенко»   городского округа 

г. Уфа РБ 

 

 

 

 

 

г. Уфа 2024 год

 

Содержание:

 

1.          Введение. 

2.          Последняя цифра степени однозначных чисел.

2.1.          Последняя цифра квадратов чисел от 0 до 9.

2.2.          Последняя цифра кубов чисел от 0 до 9.

2.3.          Последняя цифра четвертой степени   чисел от 0 до 9.  

2.4.          Алгоритм нахождения последней цифры степени.

3.          Последние две цифры степени.

3.1.          Таблица последних двух цифр степени  для чисел от 1 до 100.

3.2.          Программа на языке программирования PYTHON  для вычисления степени числа.

4.          Практическое применение работы.

4.1.          Олимпиадные  и занимательные задачи.

4.2.Математический фокус.

4.          3.Авторские задачи для самостоятельного решения.

5.          Заключение.

6.          Использованная литература.

 

 

 

1. Введение.

   На внеурочном занятии по математике учительница нам предложила следующие  задачи: 

1.     Делится ли число 46⁷+35⁵ на 10? 

2.     Найти последнюю цифру степени   24²⁵ .

    После долгих вычислений, мы задумались, может, есть легче способ решить подобные задачи? Нас очень заинтересовала эта тема, и мы решили подробнее изучить тему Степени, и выбрать тему исследовательской работы:  «Тайна последней цифры степени». В своей научно-исследовательской работе мы решили составить таблицу степеней для однозначных и двузначных чисел, и  отыскать  алгоритмы нахождения последней цифры степени.  Актуальность. Выбранная нами тема исследования имеет широкое применение при решении олимпиадных задач по математики, также при подготовке к ВПР и ЕГЭ.  В своей исследовательской работе мы выдвинули следующее предположение: существует ли алгоритм нахождения  последней цифры степени числа (кроме последовательного умножения). На основании вышесказанного мы поставили  перед собой следующую цель:  раскрыть тайны нахождения последней цифры степени. Для реализации поставленной цели нами были выдвинуты задачи: 

1)   Изучить соответствующую математическую литературу.

2)   Расширить знания о степенях, составить таблицу степеней.

3)   Написать программу на языке программирования PASCAL для составления таблицы степеней.

4)   Разработать алгоритм нахождения последней цифры степени для однозначных и для двузначных чисел.

5)   Показать практическое применение данной темы.

6)   Разработать справочник для учащихся.

     Данная исследовательская работа реализуется в предметных рамках математики и алгебры, также можно использовать на уроках физики.

Справочник для учащихся может быть использовано для внеурочной деятельности и при подготовке к Олимпиаде по математике и к ЕГЭ.

 

 

 

 

 

2.1.Последняя цифра квадратов чисел от 0 до 9      Составим таблицу квадратов однозначных чисел

Изучая таблицу, можно заметить  некоторые закономерности: 

•      Запись числа,  являющегося полным квадратом числа, может оканчиваться только на цифры 0, 1, 4, 5, 6, 9.

•      Если запись числа оканчивается цифрой 2, 3 ,7, 8, то это число не является квадратом числа.

•      Если запись числа оканчивается цифрой 0, 1 ,4, 5, 9, то квадрат числа также оканчивается цифрой 0, 1, 4, 5, 9 соответственно.

•      Если запись числа оканчивается цифрой 2 или цифрой 8, то квадрат числа оканчивается цифрой 4.

•      Если запись числа оканчивается цифрой 3 или цифрой 7, то квадрат числа оканчивается цифрой 9.

 

 

 

 

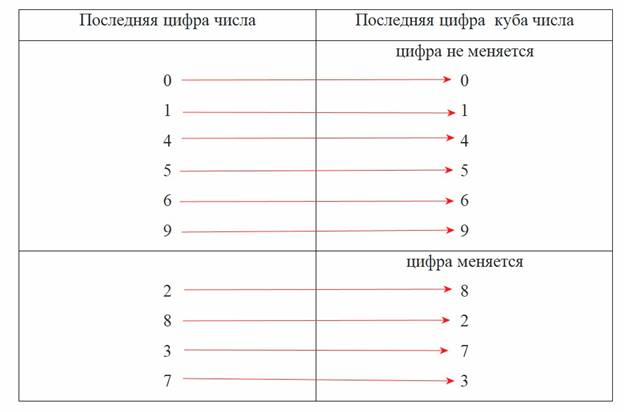
2.2. Последняя цифра кубов чисел от 0 до 9.

Используя определение степени aⁿ  = a ∙ a ∙ a ∙ ∙ ∙ a  (n = 3),  составим таблицу кубов однозначных чисел

n	0	1	2	3	4	5	6	7	8	9
n3	0	1	8	27	64	125	216	343	512	729

Изучая таблицу, можно заметить  некоторые закономерности: 

•      Запись числа,  являющегося кубом числа, может оканчиваться на любую цифру от 0 до 9.

•      Если запись числа оканчивается цифрой 0, 1, 4, 5, 6, 9,  то возведение в третью  степень не изменит последние цифры.

•      У кубов чисел 2, 3, 7, 8 последняя цифра равна разности десяти и числа, которое возводилось в куб.  Например, 7³ = 343, последняя цифра 3 может быть получена как 10 – 7.

 

 

 

 

 

2.3. Последняя цифра четвертой степени чисел от 0 до 9.    Используя определение степени aⁿ  = a ∙ a ∙ a ∙ ∙ ∙ a  (n = 4), составим таблицу 4 степени однозначных чисел

n          0          1          2          3          4          5          6          7          8          9

n⁴               0          1          16        81        256      625      1296    2401    4096      6561

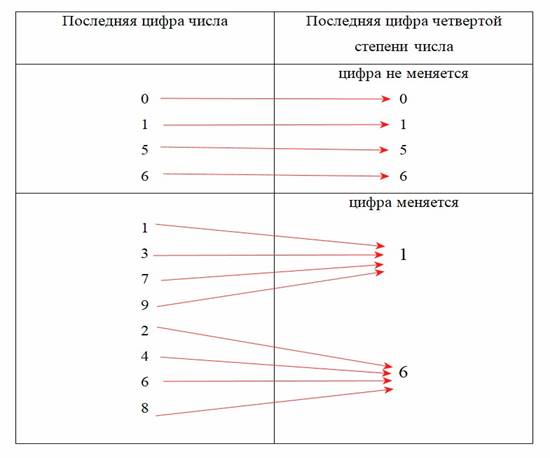
Изучая таблицу, можно заметить  некоторые закономерности: 

•      Запись числа,  являющегося четвертой  степени числа, может оканчиваться только на цифры 0, 1, 5, 6.

•      Если запись числа оканчивается цифрой 0, 1, 5, 6,  то  запись 4 степени  числа также оканчивается цифрой 0, 1, 5, 6  соответственно.

•      Если запись числа оканчивается нечетной цифрой 1, 3, 7, 9,  то четвертая степень числа оканчивается цифрой 1.

•      Если запись числа оканчивается четной цифрой 2, 4, 6, 8,  то четвертая степень числа оканчивается цифрой 6.

 

2.4. Алгоритм нахождения последней цифры степени.  

Используя определение степени aⁿ  = a ∙ a ∙ a ∙ ∙ ∙ a  (n раз), составим таблицу  степени однозначных чисел до 10 степени

n	1		2	3	4	5	6	7	8	9		10
1n	1		1	1	1	1	1	1	1	1		1
2n	2		4	8	16	32	64	128	256	512		1024
3n	3		9	27	81	243	729	2187	6561	19683		59049
4n	4		16	64	256	1024	4096	16384	65536	262144		1048576
5n	5		25	125	625	3125	15625	78125	390625	1953125		9765625
6n	6		36	216	1296	7776	46656	279936	1679616	10077696		60466176
7n	7		49	343	2401	16807	117649	823543	5764801	40353607		282475249
8n	8		64	512	4096	32768	262144	2097152	16777216	134217728		1073741824
9n	9		81	729	6561	59049	531441	4782969	43046721	387420489		3486784401
10n	10		100	1000	10000	100000	1000000	10000000	100000000	1000000000		10000000000
		Изучая таблицу, можно заметить  некоторые закономерности:

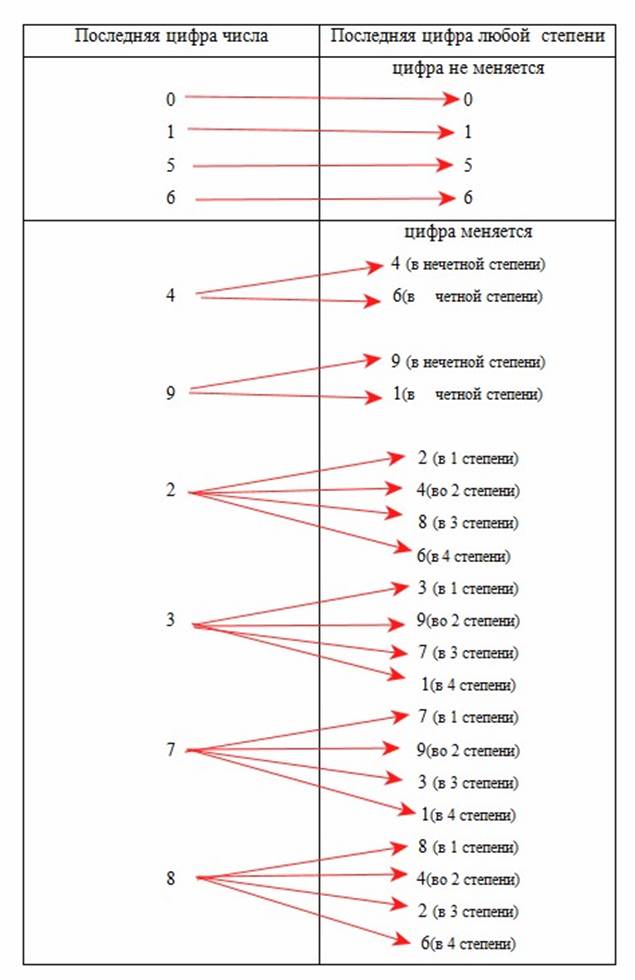
•      Если запись числа оканчивается цифрой 0, 1, 5, 6,  то возведение в любую степень не изменит последние цифры.

•      При возведении любого числа в пятую степень его последняя цифра не изменится.

•      Если запись натурального числа оканчивается цифрой 4, то при возведении в нечетную степень последняя цифра не изменится, будет также 4, а при возведении в четную степень изменится, будет 6.

•      Если запись натурального числа оканчивается цифрой 9, то при возведении в нечетную степень последняя цифра не изменится, будет также 9, а при возведении в четную степень изменится, будет 1.

•      Если запись натурального числа оканчивается цифрой 2, то при возведении в степень последняя цифра может быть 2, 4, 8, 6

•      Если запись натурального числа оканчивается цифрой 3, то при возведении в степень последняя цифра может быть 3, 9, 7, 1.

•      Если запись натурального числа оканчивается цифрой 7, то при возведении в степень последняя цифра может быть 7, 9, 3, 1.

•      Если запись натурального числа оканчивается цифрой 8, то при возведении в степень последняя цифра может быть 8, 4, 2, 6.

 

 

   Так как  при возведении любого числа в пятую степень его последняя цифра повторяется, то можно найти последние цифры степени по остатку от деления еѐ показателя на 4.

Алгоритм нахождения последней цифры степени

(при помощи деления показателя степени на число 4)

•      Если при делении  показателя степени на число 4 остаток равен 1, то последняя цифра степени будет равна последней цифре самого числа.    Пример  2⁹ = 512    9:4 = 2(остаток 1)

•      Если при делении  показателя степени на число 4  остаток равен 2, то последняя цифра степени будет равна последней цифре самого числа.   

Пример  3⁶ = 729    6:4 = 1(остаток 2)

•      Если при делении  показателя степени на число 4  остаток равен 3, то последняя цифра степени будет равна последней цифре самого числа.   

Пример  4⁷ = 16384     7:4 = 1(остаток 3)

•      Если показатель степени нацело делится на число 4, то последняя цифра степени будет равна последней цифре 4 степени числа.   Пример  6⁴ = 1296     4:4 = 1).

  Значит, чтобы найти последнюю цифру степени натурального числа с натуральным показателем, нужно найти остаток от деления показателя степени на 4. Последние цифры степеней чисел 2 , 12, 22 и т. д. (3, 13, 23 и т.д.) и т. д. будут совпадать.

Алгоритм нахождения последней степени числа  также можно объяснить  с помощью следующего свойства  степени:

am∙ an= aт+n

Показатель степени нужно разделить на 4 и представить степень в виде a^k  = a^4m+n = a^4m∙ aⁿ  (n = 0, 1, 2, 3)

Возможны случаи:

ak = a4m + 0 = a4m∙ a0 = a4m∙ 1 = a4m

a k = a4m + 1 = a4m_{∙ a}1 ak  = a4m + 2 = a4m∙ a2 ak = a4m + 3 = a4m∙ a3

На  нахождение последней цифры степени выражение    a^4m  не влияет. 

Последняя цифра степени будет такой же, какая будет последняя цифра степени  aⁿ  (n = 0, 1, 2, 3), точнее степени a¹, a², a³, a⁴.

    Например: 

                       19⁷⁶ = 19 ^{19∙ 4} (последняя цифра 1)

                        2⁴⁵ =  2^{44 + 1} =  2⁴⁴∙ 2¹ (последняя цифра 2)

                        13¹⁰² = 13^{100 + 2} =  13¹⁰⁰∙ 13² (последняя цифра 9)

                        106⁸⁷ = 106^{84 + 3} = 106⁸⁴∙ 106³ (последняя цифра 6)

 

3. Последние две цифры степени числа

3.1.Таблица последних двух цифр степеней чисел от 1 до 100

Мы составили   таблицу двух последних цифр степеней для чисел от 1 до 100  (ПРИЛОЖЕНИЕ 1). Изучая таблицу двух последних цифр чисел от 1 до 100, мы  пришли к выводу:

•      Две последние цифры начинают повторяться после возведения в некоторую степень. 

•      У некоторых чисел последние две цифры не повторяются. Но после некоторого периода начинает повторяться две последние цифры квадрата этого числа.

В следующих таблицах показано период повторения последних двух цифр степени для каждого числа или для квадрата  числа от 1 до 100:

Период повторения двух последних цифр		Число	Вывод
1		01	ответ всегда  1
2		24, 49, 51,99	закономерности нет
4		07,  32, 43, 57, 68, 93	закономерности нет
5		16, 21, 41, 56, 61, 81, 96	числа, оканчиваются на цифру 1 или 6 (но не все двузначные числа, нет 01, 11, 31, 26, 51, 76, 91)
10		04, 09, 11, 19, 29, 31, 44,  59, 64, 69, 71, 79, 84, 89, 91	числа, оканчиваются на цифру 1, 4, 9 (но не все двузначные числа)
12		39	только одно число
20		03, 08, 12, 13, 17, 23, 27, 28, 33, 37, 47, 48, 52, 53, 63, 67, 72, 73, 77,  83, 87, 88, 92, 97	числа оканчиваются цифрой 2,  3, 7 или  8
Период повторения двух последних цифр квадрата числа		Число	Вывод
1		05, 10, 20, 25, 26, 30, 40, 45, 50, 60, 65, 70, 75, 76, 80, 85, 90, 100	Закономерности нет:  все числа, оканчиваются на цифру 0        или       5        (исключение составляют числа 26 и 76)
2		15, 35,  55, 74, 95	закономерности нет
4		18, 82	закономерности        нет,           только два числа
5		06,  36, 46,  66,  86	числа, оканчиваются на цифру 6 (но не все двузначные числа)
10		14,  34, 54,  94	числа, оканчиваются на цифру 1, 4, 9 (но не все двузначные числа)
20		02,  22,  38, 42,  58, 62, 78,  98	числа оканчиваются цифрой 2  или  8

 

3.2. Программа на языке программирования PYTHON 

для вычисления степени числа

Для вычисления  степеней чисел мы составили программу на языке программирования PYTHON.. Язык программирования PYTHON можно

найти на сайте https://www.programiz.com/python-programming/online-compiler/.

 

Программа:

while True:

    # Ввод чисел x и y     x = float(input("Введите число x: "))     y = float(input("Введите степень y: "))

    # Вычисление x в степени y

    result = x ** y

    # Вывод результата без научной нотации     print("Результат: {:.0f}".format(result))

Примеры вычислений  с помощью этой программы приведены в приложении

(ПРИЛОЖЕНИЕ 2).

 

4.          Практическое применение работы

4.1.          Олимпиадные задачи 

 

    Мы изучили олимпиадные и занимательные задачи на нахождение последней цифры степени. В своей работе  показали  решения некоторых   нестандартных олимпиадных  и занимательных задач   на нахождение последней цифры степени при помощи алгоритма, которое мы разработали в своей исследовательской  работе (ПРИЛОЖЕНИЕ 3).

 

 

 

 

4.2.          Математический фокус

  Попросите кого - нибудь,  задумать двузначное число, возвести его в третью степень и продиктовать результат вычислений. Посмотрев на результат, ты сможешь сразу сообщить, какое число было задумано. 

Например, тебе показывают число 658503. Через секунду ты можешь сказать, что было задумано число 87.

Решение математического фокуса. К разгадыванию фокуса нужно подготовиться заранее. Прежде всего, нужно выписать и запомнить кубы чисел от 1 до 10:

1³ =1          2³ =8        3³ =27         4³ =64      5³ =125

6³ =216     7³ =343      8³ =512     9³ =729     10³ =1000

Замечаем, что все кубы этих чисел оканчиваются разными цифрами. При этом  если запись числа оканчивается цифрой 0, 1, 4, 5, 6, 9,  то возведение в третью  степень не изменит последние цифры. У кубов чисел 2, 3, 7, 8 последняя цифра равна разности десяти и числа, которое возводилось в куб.  Например, 7³ = 343, последняя цифра 3 может быть получена как 10 – 7. 

Таким образом, когда тебе сообщили число 658503, ты сразу можешь определить последнюю цифру задуманного двузначного числа. Это цифра 7.  Для того, чтобы определить первую цифру задуманного числа, поступают следующим образом. Отбрасывают последние три цифры полученного результата, и рассматривают оставшееся число, в нашем случае это число 658. Далее определяют, между кубами, каких чисел оно находится. Число 658 находится между кубами чисел 8 и 9. Меньшее из этих двух чисел даст первую цифру задуманного двузначного числа. Значит, в нашем случае было задумано число 87.

4.   3.Авторские задачи для самостоятельного решения  Мы составили подборку занимательных задач по теме «Последняя цифра степени»  для самостоятельного решения (ПРИЛОЖЕНИЕ 4)

 

 

 

5.   Заключение

   Математика, как никакая другая наука, развивает логическое мышление. По словам древнегреческого ученого Гиппократа «Все, что мы обретаем в мире математике, может рано или поздно пригодиться в будущем». А наш великий русский ученый Михаил Васильевич Ломоносов заметил, что «Пусть кто-нибудь вычеркнет из математики степени, и он увидит, что без них далеко не уедешь». Именно это мы попытались показать, изучая тему «Тайна последней цифры степени». В своей научно – исследовательской работе мы смогли разгадать тайну последней цифры степени числа. Изучив таблицы различных степеней чисел, мы смогли найти алгоритмы нахождения последней цифры любой степени. Увидели закономерности при возведении однозначных чисел в степени, нашли легкие способы нахождения последней цифры степени. Все алгоритмы нахождения последней цифры степени в своей работе мы оформили в виде таблиц и схем. Кроме этого, мы составили и изучили таблицу двух последних цифр степени для однозначных и двузначных чисел, и пробовали разгадать алгоритм нахождения последних двух цифр степени. Пришли к выводу, что  последние две цифры или последние две цифры квадрата числа после возведения в некоторую степень повторяются, но закономерности при этом нет. В нашей работе представлена программа на  языке программирования PYTHON для вычисления любой степени числа. В своей работе  показали  практические применения данной темы: при решении нестандартных олимпиадных и занимательных задач, при составлении математических фокусов. Олимпиадные и занимательные задачи по данной теме в работе  представлены с подробным решением. Также в работе включены авторские задачи для самостоятельного решения, и создан математический справочник для  учащихся по теме «Алгоритмы нахождения последней цифры степени» (ПРИЛОЖЕНИЕ 5). Наши планы на будущее составить таблицу для нахождения последних трех цифр степени.  Данная исследовательская работа реализуется в предметных рамках математики и алгебры, также можно использовать на уроках физики. Справочник для учащихся может быть использовано для внеурочной деятельности и при подготовке к Олимпиаде по математике и к ЕГЭ.

 

6.   Использованная литература.

1.     Интернет ресурсы.

2.     Лоповок Л.М. Тысяча проблемных задач по математике.

3.     Международный научный  журнал для школьников «Старт в науке».

4.     https://mmmf.msu.ru/archive/20122013/z6/21.html

5.     https://works.doklad.ru/view/mB02GvcQIQw/all.html.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 1

Таблица последних двух цифр степени  для чисел от 1 до 100

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	повтор
01n	01	01																					1
02n	02	04	08	16	32	64	28	56	12	24	48	96	92	84	68	36	72	44	88	76	52	04	20
03n	03	09	27	81	43	29	87	61	83	49	47	41	23	69	07	21	63	89	67	01	03		20
04n	04	16	64	56	24	96	84	36	44	76	04												10
05n	05	25	25																				1
06n	36	16	96	76	56	36																	5
07n	07	49	43	01	07																		4
08n	08	64	12	96	68	44	52	16	28	24	92	36	88	04	32	56	48	84	72	76	08		20
09n	09	81	29	61	49	41	69	21	89	01	09
10n	10	00	00
11n	11	21	31	41	51	61	71	81	91	01	11												10
12n	12	44	28	36	32	84	8	96	52	24	88	56	72	64	68	16	92	4	48	76	12		20
13n	13	69	97	61	93	9	17	21	73	49	37	81	53	89	57	41	33	29	77	01	13		20
14n	14	96	44	16	24	36	04	56	84	76	64	96											10
15n	15	25	75	25																			2
16n	16	56	96	36	76	16																	5
17n	17	89	13	21	57	69	73	41	97	49	33	61	37	29	93	81	77	9	53	01	17		20
18n	18	24	32	76	68	24																	4
19n	19	61	59	21	99	81	39	41	79	01	19												10
20n	20	00	00																				1
21n	21	41	61	81	01	21																	5
22n	22	84	48	56	32	4	88	36	92	24	28	16	52	44	68	96	12	64	08	76	72		20
23n	23	29	67	41	43	89	47	81	63	49	27	21	83	09	07	61	3	69	87	01	23		20
24n	24	76	24																				2
25n	25	25	25																				1
26n	26	76	76																				1
27n	27	29	83	41	07	89	3	81	87	49	23	21	67	09	43	61	47	69	63	01	27		20
28n	28	84	52	56	68	04	12	36	08	24	72	16	48	44	32	96	88	64	92	76	28		20
29n	29	41	89	81	49	21	9	61	69	01	29												10
30n	30	00	00																				1
31n	31	61	91	21	51	81	11	41	71	01	31												10

 

32n	32	24	68	76	32																		4
33n	33	89	37	21	93	69	77	41	53	49	17	61	13	29	57	81	73	09	97	01	33		20
34n	34	56	04	36	24	16	44	96	64	76	84	56											10
35n	35	25	75	25																			2
36n	36	96	56	16	76	36	96	56															5
37n	37	69	53	61	57	09	33	21	77	49	13	81	97	89	93	41	17	29	73	01	37		20
38n	38	44	72	36	68	84	92	96	48	24	12	56	28	64	32	16	8	4	52	76	88		20
39n	39	21	19	41	99	41	99	61	79	81	59	01	39										12
40n	40	00	00																				1
41n	41	81	21	61	01	41																	5
42n	42	64	88	96	32	44	48	16	72	24	08	36	12	04	68	56	52	84	28	76	92		20
43n	43	49	07	01	43																		4
44n	44	36	84	96	24	56	64	16	04	76	44												10
45n	45	25	25																				1
46n	46	16	36	56	76	96	16																5
47n	47	9	23	81	07	29	63	61	67	49	03	41	27	69	43	21	87	89	83	01	47		20
48n	48	04	92	16	68	64	72	56	88	24	52	96	8	84	32	36	28	44	12	76	48		20
49n	49	01	49																				2
50n	50	00	00																				1
51n	51	01	51																				2
52n	52	04	8	16	32	64	28	56	12	24	48	96	92	84	68	36	72	44	88	76	52		20
53n	53	09	77	81	93	29	37	61	33	49	97	41	73	69	57	21	13	89	17	01	53		20
54n	54	16	64	56	24	96	84	36	44	76	04	16											10
55n	55	25	75	25																			2
56n	56	36	16	96	76	56																	5
57n	57	49	93	01	57																		4
58n	58	64	12	96	68	44	52	16	28	24	92	36	88	04	32	56	48	85	72	76	08		20
59n	59	81	79	61	99	41	19	21	39	01	59												10
60n	60	00	00																				1
61n	61	21	81	41	01	61																	5
62n	62	44	28	36	32	84	08	96	52	24	88	56	72	64	68	16	92	04	48	76	12		20
63n	63	69	47	61	43	09	67	21	23	49	87	81	03	89	07	41	83	29	27	01	63		20
64n	64	96	44	16	24	36	4	56	84	76	64												10
65n	65	25	25																				1
66n	66	56	96	36	76	16	56																5
67n	67	89	63	21	07	69	23	41	47	49	83	61	87	29	43	81	27	09	03	01	67		9
68n	68	24	32	76	68																		4
69n	69	61	09	21	49	81	89	41	29	01	69												10
70n	70	00	00																				1
71n	71	41	11	81	51	21	91	61	31	01	71												10
72n	72	84	48	56	32	4	88	36	92	24	28	16	52	44	68	96	12	64	08	76	72		20
73n	73	29	17	41	93	89	97	81	13	49	77	21	33	09	57	61	53	69	37	01	73		20
74n	74	76	24	76																			2
75n	75	25	25																				1
76n	76	76	76																				1
77n	77	29	33	41	57	89	53	81	37	49	73	21	17	09	93	61	97	69	13	01	77		20
78n	78	84	52	56	68	04	12	36	8	24	72	16	48	44	32	96	88	64	92	76	28		20
79n	79	41	39	81	99	21	59	61	19	01	79												10
80n	80	00	00																				1
81n	81	61	41	21	01	81																	5
82n	82	24	68	76	32	24																	4
83n	83	89	87	21	43	69	27	41	03	49	67	61	63	29	07	81	23	09	47	01	83		20
84n	84	56	4	36	24	16	44	96	64	76	84												10
85n	85	25	25																				1
86n	86	96	56	16	76	36	96																5
87n	87	69	03	61	07	09	83	21	27	49	63	81	47	89	43	41	67	29	23	01	87		20
88n	88	44	72	36	68	84	92	96	04	24	12	56	28	64	32	16	08	04	52	76	88		20
89n	89	21	69	41	49	61	29	81	09	01	89												10
90n	90	00	00																				1
91n	91	81	71	61	51	41	31	21	11	01	91												10
92n	92	64	88	9	32	44	48	16	72	24	8	36	12	04	68	56	52	84	28	76	92		20
93n	93	49	57	01	93																		4
94n	94	36	84	96	24	56	64	16	04	76	44	36											10
95n	95	25	75	25																			2
96n	96	16	36	56	76	96																	5
97n	97	09	73	81	57	29	13	61	17	49	53	41	77	69	93	21	37	89	33	01	97		20
98n	98	04	92	16	68	64	72	56	88	24	52	96	08	04	32	36	28	44	12	76	04		20
99n	99	01	99																				2
100	0	0	0																				1

  

 

 

 

 

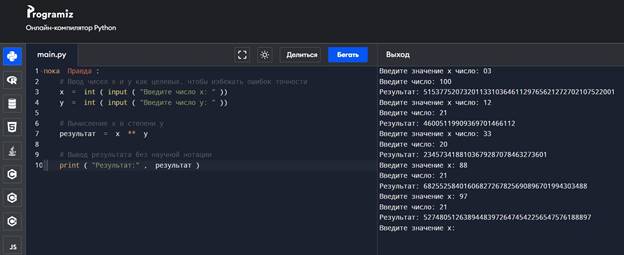
ПРИЛОЖЕНИЕ 2 Программа на языке программирования PYTHON  для вычисления степени числа

Примеры  вычислений

 

 

 

 

ПРИЛОЖЕНИЕ 3

Олимпиадные и занимательные задачи:

1.  Найти последнюю цифру числа: 

100       

А) 3

 Решение. 3100  = 325*4. 

Последняя цифра равна последней цифре числа 3⁴ = 81.

Ответ. 1

49    

Б) 549

 Решение. 549⁴⁹. Если запись натурального числа оканчивается цифрой 9, то при возведении в нечетную степень последняя цифра не изменится, будет также 9, а при возведении в четную степень изменится, будет 1.

Число 49 нечетное, значит, последняя цифра степени равна 9.  Ответ. 9

2024   

В) 2024

Решение.  Если запись натурального числа оканчивается цифрой 4, то при возведении в нечетную степень последняя цифра не изменится, будет также 4, а при возведении в четную степень изменится, будет 6.

Число 2024 четное, значит, последняя цифра степени равна 6.

Ответ. 6.

666

Г) 666

Решение. Если запись числа оканчивается цифрой 6,  то возведение в любую степень не изменит последние цифры.

Ответ. 6.

2.     В книге рекордов Гиннеса написано, что наибольшее известное

337 – 1. Не опечатка ли это? простое число равно 23021

Решение. Число 23021³³⁷ оканчивается цифрой 1 (цифра не меняется). Поэтому последняя цифра числа (23021³³⁷ – 1) равна 0, а это значит, что это число делится на 10, и поэтому оно не простое, а составное.

Ответ. Опечатка.

 

3.     Делится ли число 47³⁰ + 39⁵⁰ на 10?

Решение. Число 47³⁰ = 47²⁸⁺² = 47²⁸ ∙ 47² , поэтому оканчивается цифрой 9,также  как 7², а число 39⁵⁰ = 39⁴⁸⁺² = 39⁴⁸ ∙ 39² , поэтому оканчивается цифрой 1, также как 9². Значит, их сумма оканчивается  цифрой 0 и потому делится на 10.

Ответ. Делится.

4.     Найти последнюю цифру в произведении всех нечетных чисел от 1 до  2024.

Решение.  Это произведение делится на 5, но не делится на 2. Поэтому в силу признаков делимости на 2 и 5 оно может оканчиваться только цифрой 5.

Ответ. 5.

5.     Найти последнюю цифру числа .

Решение. Последние две цифры числа 7⁷= 823543  образуют число 43. Значит, 7⁷  делится на 4 с остатком 3. Если запись натурального числа оканчивается цифрой 7, то при возведении в степень последняя цифра может быть 7, 9, 3, 1. Так как остаток от деления показателя степени равна 3, значит, последняя цифра  степени равна 3.

Ответ. 3.

6.     Докажите, что число 4³⁴⁵ + 456⁴  является составным. 

Решение. Число 4³⁴⁵ оканчивается цифрой 4, так как, если запись натурального числа оканчивается цифрой 4, то при возведении в нечетную степень последняя цифра не изменится, будет также 4, а при возведении в четную степень изменится, будет 6. А число 456⁴ оканчивается цифрой 6, так как если запись числа оканчивается цифрой 6,  то возведение в любую степень не изменит последнюю цифру. Значит, их сумма оканчивается  цифрой 0 и потому делится на

10. Так как  число делится на 10, и поэтому оно, а составное.

 

 

                7.         Задача из книги «Тысяча проблемных задач по математике»:

Найти последнюю цифру суммы 

11989 + 21989+ 31989+ 41989+ 51989+ 61989+ 71989+ 81989_{+ … +1988}1989+ 19891989  

Ответ. 5

8.     Сейчас на часах 10:00. Какое время они будут показывать через 102938475 часов? 

Решение. У часов период повторения равен 24, значит число

102938475 разделить на 24 = 4289103,12… 102938475 – (4289103 *

24) = 3. Значит время которое часы будут показывать через 102938475 часов равно 10+3 = 13 часов. Ответ: через 102938475 часы будут показывать 13:00.  

ПРИЛОЖЕНИЕ 4

Авторские задачи для самостоятельного решения

1.     Найдите последнюю цифру числа:

А) 2024²⁰²⁰

Б) 2024²⁰²¹

В) 2024²⁰²²

Г) 2024²⁰²³

Д) 2024²⁰²⁴ Е) 2024²⁰²⁵

2.     Докажите, что среди квадратов любых пяти натуральных чисел всегда можно выбрать два, сумма или разность которых делится на 10.

Решение. Квадрат любого натурального числа оканчивается на 0, 1, 4, 5, 6 или 9. Если в наборе есть два квадрата, оканчивающиеся на две одинаковые цифры, при их вычитании получится число с нулѐм на конце, а значит, делящееся на 10. Если же все пять последних цифр квадратов в наборе различны, то среди них обязательно будет либо пара 4, 6, либо пара 1, 9. Тогда сложим эти квадраты и тоже получим число с нулѐм на конце, а значит, делящееся на 10.

3.     А) Докажите что число 3⁸²+2⁹¹ не делится на 5 без остатка.      Б)  Докажите что число 3⁸²+7⁹¹  четное.

     В)  Докажите что число 3⁸²+11⁹¹ делится на 10 без остатка.

     Г) Докажите что число 3⁸²+2⁹¹ делится на 4 без остатка.

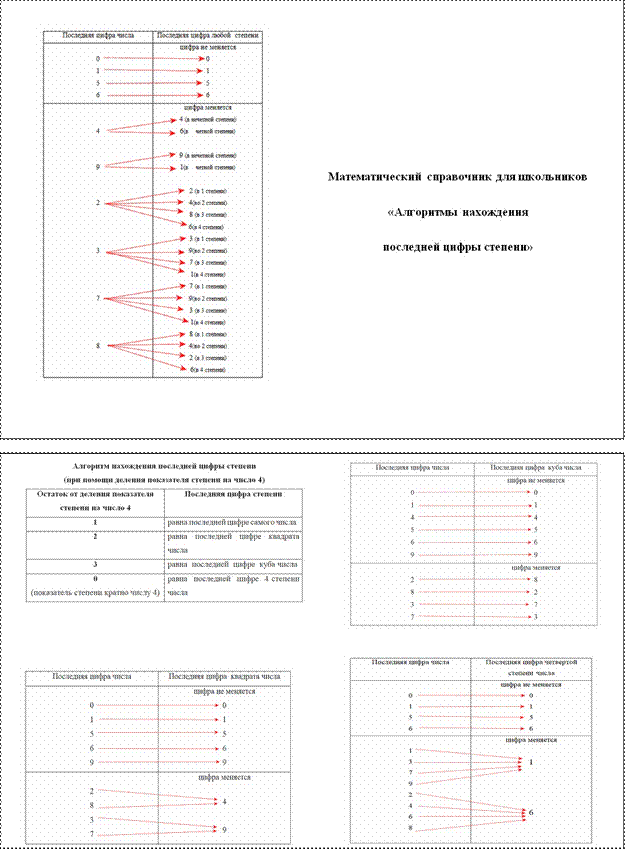
ПРИЛОЖЕНИЕ 5

Математический справочник для школьников 

«Алгоритмы нахождения последней цифры степени»