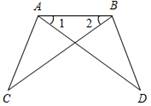
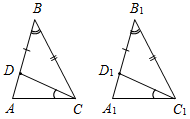
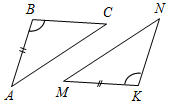
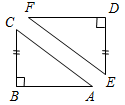
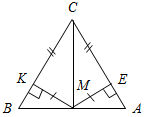
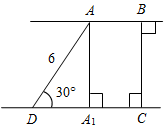
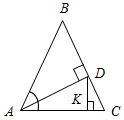
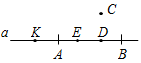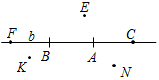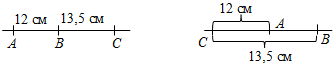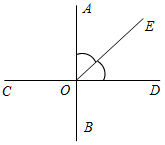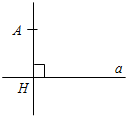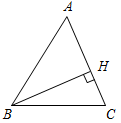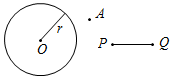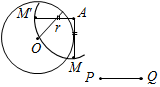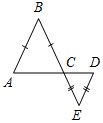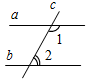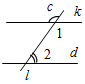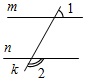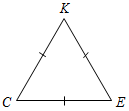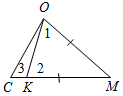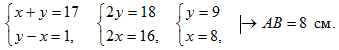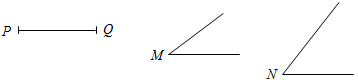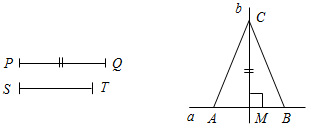Технологические карты уроков по геометрии для 7 класса( Л. С. Атанасян и др.)
Урок 1. Прямая и отрезок
|
Цель деятельности учителя |
Создать условия для систематизации знаний о взаимном расположении точек и прямых, ознакомления учащихся со свойством прямой (через любые две точки можно провести прямую и притом только одну), рассмотрения приема практического проведения прямых на плоскости (провешивание) |
|
|
Термины и понятия |
Отрезок, прямая, точка, плоскость |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления |
Познавательные: владеют первоначальными сведениями об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют находить в различных источниках информацию, необходимую для решения математических проблем. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Геометрия. 7–9 классы: учеб. для общеобразоват. организаций / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. М.: Просвещение, 2014*. • Задания для фронтальной и самостоятельной работы. • Сведения из истории возникновения и развития науки геометрии |
|
|
I этап. Вводная беседа |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Познакомить с предметом «геометрия» |
(Ф/И) Учитель рассказывает о науке «геометрия»; учащиеся слушают, задают уточняющие вопросы (см. Ресурсный материал) |
|
|
II этап. Учебно-познавательная деятельность. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Ввести основные понятия геометрии и основную символику |
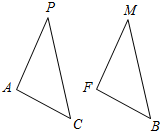
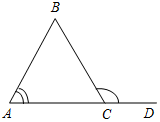
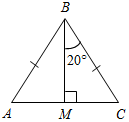
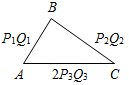
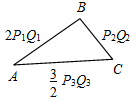
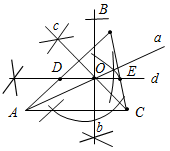
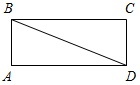
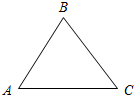
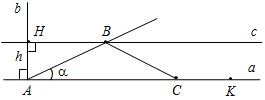
(Ф/И) К доске для выполнения заданий вызывается по одному учащемуся, остальные работают в тетрадях. Учитель читает задание и по мере необходимости вводит новые понятия, символы, делает необходимые записи на доске. 1) Начертите прямую. Как ее можно обозначить? (Прямая а или АВ.)
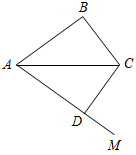
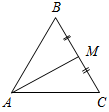
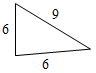
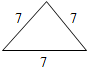
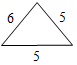
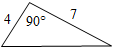
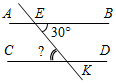
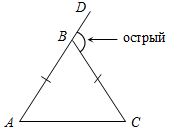
Рис. 1 2) Отметьте точку С, не лежащую на данной прямой, и точки D, Е, K, лежащие на прямой.
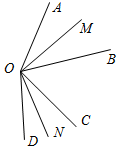
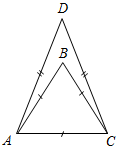
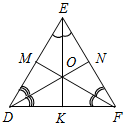
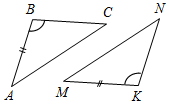
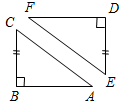
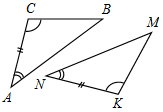
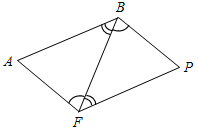
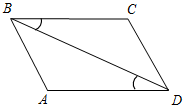
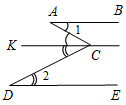
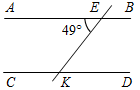
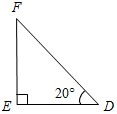
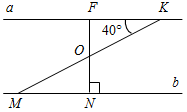
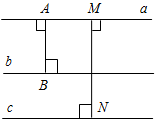
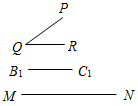
Рис. 2 – В математике существуют специальные символы, позволяющие кратко записать какое-либо утверждение. Символы Î и Ï означают соответственно «принадлежит» и «не принадлежит» и называются символами принадлежности. 3) Используя символы принадлежности, запишите предложение «Точка D принадлежит прямой АВ, а точка С не принадлежит прямой а». (D Î АВ, С Ï а.) 4) Используя рисунок и символы Î и Ï, запишите, какие точки принадлежат прямой b, а какие – нет. (F, В, А, С Î b; K, Е, N Ï b.)
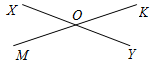
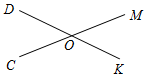
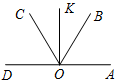
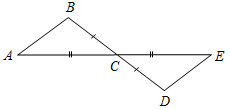
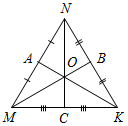
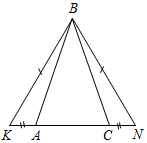
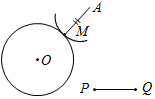
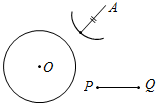
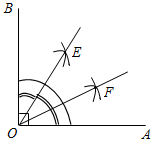
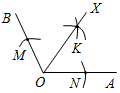
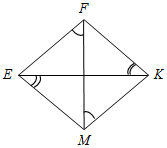
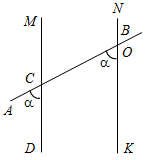
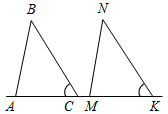
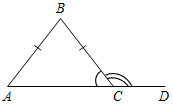
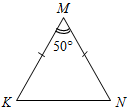
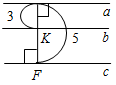
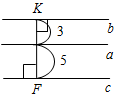
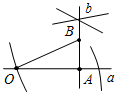
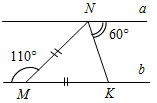
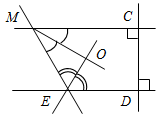
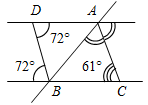
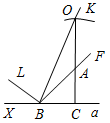
Рис. 3 – Сколько прямых можно провести через заданную точку А? (Через заданную точку А можно провести множество прямых.) – Сколько прямых можно провести через две точки? (Одну прямую.) – Через любые две точки можно провести прямую? (Да.) – Итак, через любые две точки можно провести прямую и притом только одну. Это утверждение назовем свойством прямой. 5) Начертите прямые XY и МK, пересекающиеся в точке О.
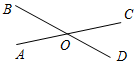
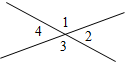
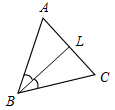
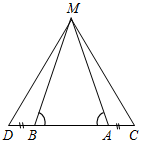
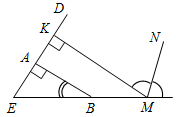
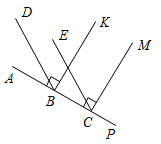
Рис. 4 – Для того чтобы кратко записать, что прямые ХY и МK пересекаются в точке О, используют символ Ç и записывают так: XYÇМK = О. – Сколько общих точек может быть у двух прямых? (Две прямые могут иметь или одну общую точку, или ни одной общей точки.) 6) На прямой а отметьте последовательно точки А, В, С, D. Запишите все получившиеся отрезки. (Получились отрезки АВ, ВС, CD, AC, AD, BD.)
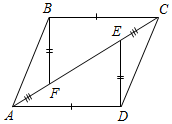
Рис. 5 |
|
|
III этап. Выполнение практических заданий |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Выявить уровень |
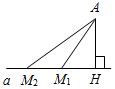
(Ф/И) 1. Выполнение практических заданий № 2, 3 на с. 7 учебника. 2. Вопросы к учащимся: – Могут ли прямые ОА и АВ быть различными, если точка О лежит на прямой АВ? (Прямые ОА и АВ не могут быть различными, так как обе они проходят через точки А и О, а через две точки проходит только одна прямая.) – Даны две прямые а и b, пересекающиеся в точке С, и точка D, отличная от точки С и лежащая на прямой а. Может ли точка D лежать на прямой b? (Точка D не может лежать на прямой b, так как две прямые не могут иметь двух общих точек.) 3. Введение понятия отрезка (используется рис. 7 учебника). 4. Самостоятельное выполнение учащимися задания № 5. 5. Изложение материала п. 2 «Провешивание прямой на местности» в виде беседы (по рис. 8 и 9 учебника) |
|
|
IV этап. Самостоятельная работа |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Выявить уровень сформированности теоретических знаний и практических умений учащихся |
(И) Самостоятельная работа проводится в форме диктанта на листках и сдается на проверку учителю. 1. Начертите прямую и обозначьте ее буквой b. 1) Отметьте точку М, лежащую на прямой b. 2) Отметьте точку D, не лежащую на прямой b. 3) Используя символы Î и Ï, запишите
предложение: «Точка М лежит на прямой b, а точка D не
лежит 2. Начертите прямые а и b, пересекающиеся в точке K. На прямой а отметьте точку С, отличную от точки K. 1) Являются ли прямые KС и а различными прямыми? Ответ обоснуйте. 2) Может ли прямая b проходить через точку С? Ответ обоснуйте. 3*. Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки. 4*. На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки |
|
|
V этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Что изучает предмет «геометрия»? – Когда он появился? – Зачем он нужен? |
(И) Домашнее задание: пункты 1, 2; ответить на вопросы 1–6 на с. 25 учебника; практические задания № 4, 6, 7 |
|
Ресурсный материал
Геометрия – это наука о свойствах геометрических фигур. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Такое название связано с применением геометрии для измерений на местности. Геометрия возникла в результате практической деятельности людей: нужно было сооружать жилища, храмы, проводить дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры. Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических знаний. За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические представления, которые формировались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построения прямых углов и т. д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории. Первым, кто начал получать новые геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI в. до н. э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и т. д., то есть то, что на современном геометрическом языке называется движением. Постепенно геометрия становится наукой, в которой большинство фактов устанавливается путем рассуждений, доказательств.
Попытки греческих ученых привести геометрические факты в систему начинаются уже в V в. до н. э. Наибольшее влияние на все последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III в. до н. э. Сочинение Евклида «Начала» почти 2000 лет служило основной книгой, по которой изучали геометрию. В «Началах» были систематизированы известные к тому времени геометрические сведения и геометрия впервые была представлена как математическая наука. Работа содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней подведен итог предшествующему развитию греческой математики и создан фундамент для дальнейшего развития этой науки. Книга была переведена на множество языков, а геометрия, изложенная в ней, стала называться евклидовой геометрией.

Сведения о самом Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в III веке до н. э. Евклид – первый математик александрийской школы, автор работ по астрономии, оптике, музыке и др. Из других его сочинений по математике стоит отметить работу «О делении фигур», сохранившуюся в арабском переводе, четыре книги «Конические сечения», материал которых вошел в произведение с таким же названием АполлонияПергского, а также «Поризмы», представление о которых можно получить из «Математического собрания» Филона Александрийского.
В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и т. д. Отвлекаясь от этих свойств и обращая внимание только на форму и размеры предметов, мы приходим к понятию геометрической фигуры.
На уроках математики вы познакомились с некоторыми геометрическими фигурами и представляете себе, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга. Вы знакомы и с такими фигурами, как треугольник, прямоугольник, круг (продемонстрировать модели фигур).
Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить.
Школьный курс геометрии делится на планиметрию и стереометрию. Такие фигуры, как отрезок, луч, прямая, угол, окружность, круг, треугольник, прямоугольник, являются плоскими, то есть целиком укладываются на плоскости. Раздел геометрии, изучающий свойства фигур на плоскости, называется планиметрией (от латинского слова «планум» – плоскостьи греческого «метрео» – измеряю). В стереометрии изучаются свойства фигур в пространстве, таких как параллелепипед, шар, цилиндр, пирамида (продемонстрировать модели). Мы начнем изучение геометрии с планиметрии.
Урок 2. Луч и угол
|
Цель деятельности учителя |
Создать условия для актуализации знаний учащихся о том, что такое луч и угол, введения на наглядном уровне понятий внутренней и внешней областей неразвернутого угла, ознакомления с различными обозначениями лучей и углов |
|
|
Термины и понятия |
Отрезок, прямая, точка, плоскость, луч, угол, внутренняя область угла, внешняя область угла |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления |
Познавательные: владеют первоначальными сведениями об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют находить в различных источниках информацию, необходимую для решения математических проблем. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для фронтальной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать |
(Ф/И) 1. Проверить правильность выполнения домашнего задания. Для этого к доске вызвать двоих учащихся, которые представляют свои решения. 2. Сообщить итоги математического диктанта |
|
|
II этап. Учебно-познавательная деятельность |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Ввести понятия угла |
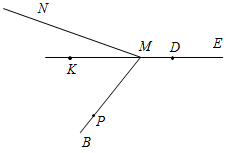
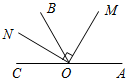
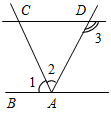
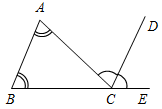
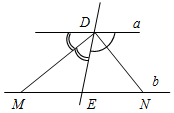
(Ф/И) 1. Введение понятия луча (использовать рис. 11 учебника). 2. Обозначение луча (рис. 12 а и б). 3. Выполнение практических заданий: 1) Проведите прямую а. а) Отметьте на ней точки А, В и С так, чтобы точка А лежала между точками В и С. б) Назовите лучи, исходящие из точки А. в) Отметьте на луче АВ точку D. 2) Укажите все лучи, изображенные на рисунке: а) исходящие из точек М и D; б) составляющие вместе с их общим началом одну прямую.
4. Самостоятельное выполнение практического задания № 8. 5. Объяснение темы «Угол». 1) На модели показывается, из каких элементов состоит данная фигура. 2) Дается определение угла. 3) Вводятся различные способы обозначения угла. 4) Вводятся понятия развернутого и неразвернутого угла (рис. 15 а и б) |
|
|
III этап. Решение задач |
||
|
Деятельность учителя |
Совместная деятельность |
|
|
Совершенствовать навыки решения задач |
(Ф/И) 1. Выполнение практических заданий № 9, 10 и 11 на доске и в тетрадях. 2. Выполнение заданий: 1) Начертить неразвернутый
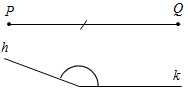
угол hk, заштриховать его внутреннюю область, провести луч l,
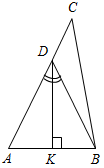
исходящий Учащиеся делают вывод, что если угол hk развернутый, то любой луч, исходящий из его вершины и не совпадающий с лучами h и k, также делит этот угол на два угла (рис. 16б). 2) Выполнить практическое задание № 14. 3) Устно решить задания № 15, 16 (по рис. 17) и задание № 17 (по рис. 18) |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какая геометрическая фигура называется углом? – Из каких элементов он состоит? – Составьте синквейн к уроку |
(И) Домашнее задание: изучить пункты 3, 4 из § 2; ответить на вопросы 4–6 на с. 25 учебника; выполнить практические задания № 12–13 |
|
Урок3. Сравнение отрезков и углов
|
Цель деятельности учителя |
Создать условия для введения одного из важнейших геометрических понятий – понятия равенства фигур, в частности равенства отрезков и углов; для обучения учащихся сравнению отрезков и углов, введения понятий середины отрезка и биссектрисы угла |
|
|
Термины и понятия |
Отрезок, прямая, точка, плоскость, луч, угол, биссектриса угла, середина отрезка |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления |
Познавательные: владеют первоначальными сведениями об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют находить в различных источниках информацию, необходимую для решения математических проблем. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для самостоятельной работы |
|
|
I этап. Актуализация опорных знаний. Вводное повторение |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать теоретический материал |
(Ф) Вопросы к учащимся: 1) Назовите основные геометрические фигуры на плоскости. 2) Что такое планиметрия? 3) Как можно обозначить прямую? 4) Что называется отрезком? 5) Сколько общих точек могут иметь две прямые? 6) Сколько прямых можно провести через любые две точки плоскости? 7) Объясните, что такое луч. Как обозначаются лучи? 8) Какая фигура называется углом? Объясните, что такое вершина и стороны угла. 9) Какой угол называется развернутым? 10) Сколько неразвернутых
углов образуется при пересечении трех прямых, проходящих через одну точку? |
|
|
II этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Ввести понятие биссектрисы угла |
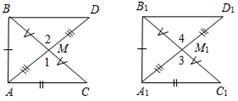
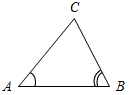
(Ф) Введение понятия равенства фигур. Вывод: две геометрические фигуры называются равными, если их можно совместить наложением. 1) Сравнение фигур. – Задача сравнения фигур (их форм и размеров) является одной из основных в геометрии. На практике сравнить наложением две небольшие плоские фигуры вполне возможно, а вот два очень больших стекла, а тем более два земельных участка практически невозможно. Это приводит к выводу о необходимости определенных правил сравнения двух фигур, позволяющих сравнить некоторые их размеры и по результатам этого сравнения сделать вывод о равенстве или неравенстве данных фигур. (Можно предложить учащимся сравнить некоторые фигуры наложением кальки.) 2) Работа по рис. 20 учебника. Запись в тетрадях: ВK = DМ (равные отрезки); АС <АВ. 3) Введение понятия середины отрезка (рис. 21). 4) Решение задач № 19 и 20 (по рис. 25). 5) Работа по рис. 22 и 23 учебника. 6) Выполнение задания № 21 на доске и в тетрадях. 7) Введение понятия биссектрисы угла (рис. 24). 8) Решение задачи № 22 (устно) |
|
|
III этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
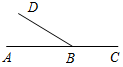
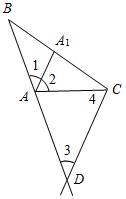
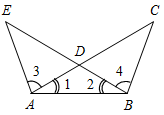
(Ф/И) 1. Самостоятельная работа в форме диктанта. 1) На луче h с началом в точке О отложите отрезки ОА и ОВ так, чтобы точка А лежала между точками О и В. Сравните отрезки ОА и ОВ и запишите результат сравнения. 2) Начертите неразвернутый угол АВС и проведите произвольный луч ВD, делящий этот угол на два угла. Сравните углы АВС и АВD, АВС и DВС и запишите результаты сравнения. 2. Решение задач. № 1. На прямой а от точки А
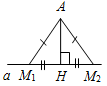
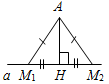
отложены два отрезка АВ и АС, причем АВ<АС<
1,99АВ. Сравните отрезки ВС и АВ
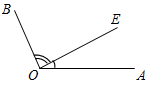
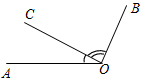
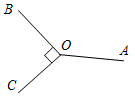
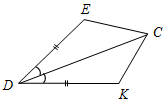
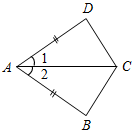
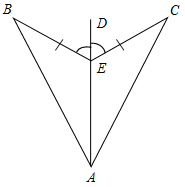
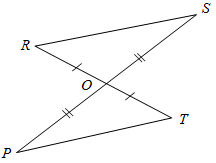
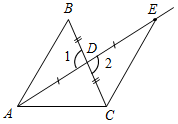
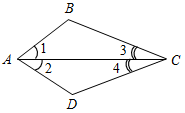
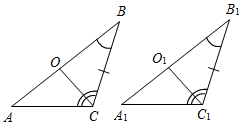
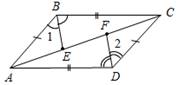
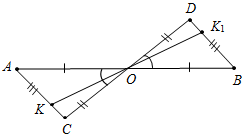
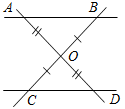
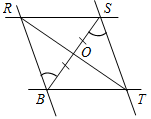
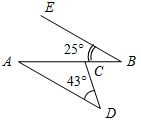
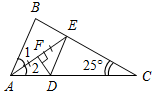
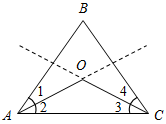
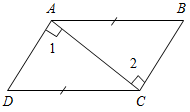
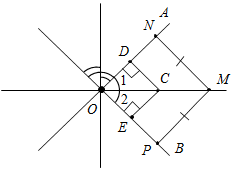
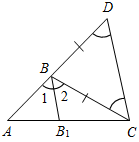
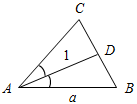
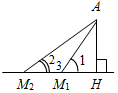
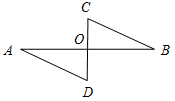
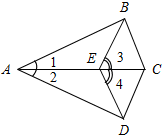
а) Рис. 1 б) № 2. ÐAOC = ÐBOD, ОМ и ON – биссектрисы углов АОВ и COD. Сравните углы MON и АОС. (ÐAOB = ÐCOD, так как ÐAOC = ÐBOD, a ÐВОС – общая часть углов АОС и BOD. Так как ОМ и ON – ÐAOC = ÐАОМ + ÐМОВ + ÐВОС, ÐMON = ÐМОВ + ÐВОС + ÐCONÞÐMON = ÐAOC.)
Рис. 2 |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какие фигуры называются равными? – Что такое биссектриса угла? – Задайте три вопроса по теме |
(И) Домашнее задание:
изучить пункты 5 и 6 из § 3; ответить на вопросы 7–11 |
|
Урок 4. Измерение отрезков
|
Цель деятельности учителя |
Создать условия для ознакомления учащихся с процедурой измерения отрезков, введения понятия длины отрезка и рассмотрения свойств длин отрезков, ознакомления с различными единицами измерения и инструментами для измерения отрезков |
||||
|
Термины и понятия |
Отрезок, прямая, точка, середина отрезка |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления |
Познавательные: владеют первоначальными сведениями об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение. Личностные: имеют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||||
|
Образовательные |
• Задания для фронтальной и самостоятельной работы |
||||
|
I этап. Актуализация опорных знаний |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Выявить трудности, возникшие при выполнении домашнего задания |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Проверить правильность решения домашней работы. Для этого вызвать к доске троих учащихся |
||||
|
II этап. Учебно-познавательная деятельность |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Способствовать изучению
новой темы, используя текст |
(Ф/И) Учащимся предлагается прочитать самостоятельно § 4 «Измерение отрезков» и ответить на вопросы,записанные на доске. – Какие основные единицы
измерения длины нам известны? А дополнительные? (Основные единицы
измерения длины отрезка: мм, см, дм, м, км; дополнительные единицы измерения
длины отрезка: световой год – Как найти длину отрезка, если точка делит его на два отрезка, длины которых известны? (Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков.) – Какими инструментами пользуются для измерения расстояний? (Для измерения расстояний используются масштабная миллиметровая линейка, штангенциркуль, рулетка.) |
||||
|
III этап. Решение задач |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Закрепить полученные знания |
(Ф/И) Учитель показывает оформление решения задачи на доске, объясняя, как из условия задачи выделить, что дано и что требуется найти или доказать. 1. Решить задачу № 32 (письменно; один ученик у доски, остальные – в тетрадях). 2. Решить задачи № 30, 31 (б) на доске и в тетрадях. 3. Выполнить задания и сделать необходимые краткие записи на доске и в тетрадях. 1) Дан луч h с началом в точке О; ВÎh, АÎh; точка В лежит между точками О и А. а) Какой из отрезков: ОВ или ОА – имеет бо́льшую длину? б) Найдите АВ, если ОА = 72 см, ОВ = 4,2 дм. 2) Начертите прямую а и отметьте точку А, не лежащую на этой прямой. С помощью масштабной линейки и циркуля отметьте на прямой а точку D, удаленную от точки А на расстояние 3 см. (Выяснить вместе с учащимися, что задача может иметь одно или два решения, а может и не иметь решений.) 4. Решить задачу № 29 учебника. 5. Выполнить задание. Начертите отрезок СD, равный 5 см. С помощью масштабной линейки отметьте на прямой СD точку В, такую, что СВ = 2 см. а) Сколько таких точек можно отметить на прямой СD? б) Какова длина отрезка ВD? Рассмотрите все возможные случаи |
(И)
№ 32. Дано: А, В, СÏа, АВ = 12 см, ВС = 13,5 см. Найти: АС. Решение: На прямой а отметим точки А, В, С. Возможны случаи: а) Точка В лежит
между точками А и С, тогда б) Точка А лежит
между точками В и С, тогда в) Точка С не может лежать между точками А и В, так как АВ<ВС.
а) б) Ответ: 25,5 см или 1,5 см |
|||
|
IV этап. Самостоятельная работа |
|||||
|
Цель деятельности |
Задания для самостоятельной работы |
||||
|
Проверить уровень сформированности теоретических знаний и практических навыков |
(И) Решить задачи № 28, 27, 31, 34 из учебника. Дополнительные задачи для тех, кто справился с работой. № 1. Длина отрезка АВ равна 14 см. Найдите на прямой все такие точки D, для которых DA = 3DB. Ответ: если DÎАВ, то AD = 10,5 см, DB = 3,5 см; если ВÎАD, то DB = 7 см, AD = 21 см. № 2. Точки А, В и С лежат на одной прямой, причем длина отрезка ВС больше длины отрезка АС в 3 раза, а длина АВ меньше длины ВС на 3,6 см. Найдите длину отрезка АС. Ответ: АС = 3,6 см |
||||
|
IV этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) – Как измерить отрезки и сравнить их? – Составьте синквейн к уроку |
(И) Домашнее задание: изучить пункты 7, 8 из § 4; ответить на вопросы 12 и 13, с. 25; решить задачи № 24, 25, 28, 33, 36 (решение задачи приведено в учебнике) |
||||
Урок5. Решение задач по теме «Измерение отрезков»
|
Цели деятельности |
Создать условия для обучения учащихся решению задач на нахождение длины части отрезка или всего отрезка; способствовать развитию логического мышления |
|
|
Термины и понятия |
Отрезок, прямая, точка, середина отрезка |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления |
Познавательные: имеют первоначальные сведения об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Чертежи к задачам. • Задания для самостоятельной работы |
|
|
I этап. Актуализация опорных знаний |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Выявить трудности, возникшие при выполнении домашнего задания |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Проверить правильность выполнения домашнего задания |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
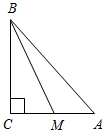
(Ф/И) 1. Решить задачи по рисункам (устно;рисунки подготовлены на доске заранее). а) Дано: ВС = 2,5 см. б) Дано: AD = 42 см, ВС = 11 см. в) Дано: АВ : АС = 4 : 5; АС = 12,5 дм. Найти: АС. Найти: АВ. Найти: АВ.
Рис. 1 Рис. 2 Рис. 3 Ответ: АС = 5 см. Ответ: АВ = 20 см. Ответ: АВ = 10 дм. 2. Решить задачи № 38, 40 (письменно). № 38. Дано: О, А, В лежат на одной прямой, ОА = 12 см, ОВ = 9 см. Найти: расстояние между серединами отрезков ОА и ОВ. Решение: Пусть М – середина отрезка ОА, N – середина отрезка ОВ. Возможны два случая:
а) Рис. 4 б) а) Если точка О лежит на отрезке АВ, то МО = АО : 2 = 6 см, NО = ВО : 2 = 4,5 см. Расстояние между серединами отрезков ОА и ОВ равно длине отрезка MN, a MN = МО + ON = 6 см + 4,5 см = 10,5 см. б) Если точка О не
лежит на отрезке АВ, то МО = АО : 2 = 6 см, NО = ВО
: 2 = 4,5 см, MN = МО – ON = Ответ: а) 10,5 см; б) 1,5 см. № 40 (предложить учащимся решить самостоятельно, а затем проверить решение задачи). Дано: АВ = 28 см; С, DÎАВ; М – середина AC; N – середина DB; MN = 16 см. Найти: CD.
Рис. 5 Решение: АВ = AM + MN + NB; АМ + NB = AB
– MN = 28 см – 16 см = 12 см. М – середина АС, значит, АМ
= MС; Так как АМ + NB
= 12 см, АМ = МС, BN = ND, то MC + DN
= 12 см. MN = МС + CD + DN = 16 см, Ответ: 4 см |
|
|
III этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Проверить уровень |
(И) Работа выполняется на листочках и сдается на проверку учителю. Вариант I 1. На отрезке АВ взяты точки С и D. Найдите длину отрезка CD, если АВ = 12 см, АС = 3 см, BD = 4 см. 2. На отрезке АВ длиной 36 см взята точка K. Найдите длину отрезков АK и ВK, если АK больше ВK на 4 см. 3. На прямой отмечены точки А, В, С так, что АВ = 27 м, АС = 11 м, ВС = 16 м. Какая из этих точек лежит между двумя другими? Вариант II 1. На отрезке АВ
взята точка С, а на отрезке СВ – точка D. Найдите длину
отрезка BD, если АВ = 15 см, 2. На отрезке АВ длиной 36 см взята точка K. Найдите длину отрезков АK и ВK, если АK больше ВK в 3 раза. 3. На прямой отмечены точки А, В, С так, что АВ = 7 м, АС = 21 м, ВС = 28 м. Какая из этих точек лежит между двумя другими? |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Оцените свою работу на уроке. – Какие задания вызвали у вас наибольшие затруднения? |
(И) Домашнее задание: решить задачи № 35, 37, 39 |
|
Урок6. Измерение углов
|
Цель деятельности учителя |
Создать условия для введения понятия градусной меры угла и рассмотрения свойств градусных мер углов, введения понятий острого, прямого и тупого углов, ознакомления учащихся с приборами для измерения углов на местности |
|
|
Термины и понятия |
Градус, минута, секунда, угол |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления |
Познавательные: выдвигают гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); коллективная (К) |
|
|
Образовательные |
• Задания для самостоятельной и фронтальной работы. • Вопросы для викторины |
|
|
I этап. Актуализация опорных знаний |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Систематизировать |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Самостоятельная работа на 10 минут с взаимопроверкой. Вариант I 1. На прямой b отмечены точки С, D и Е так, что СD = 6 см, DЕ = 8 см. Какой может быть длина отрезка СЕ? Ответ: СЕ = 14 см или СЕ = 2 см. 2. Точка М – середина отрезка АВ; МВ = 4,3 дм. Найдите длину отрезка АВ в миллиметрах. Вариант II 1. На прямой m отмечены точки А, В и С так, что АС = 12 см, АВ = 8 см. Какой может быть длина отрезка ВС? Ответ: ВС = 20 см или ВС = 4 см. 2. Точка Р – середина отрезка MN. Найдите длину отрезка PN в метрах, если MN = 14 дм |
||
|
II этап. Изучение нового материала. Учебно-познавательная деятельность |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ввести понятия единиц
измерения углов |
(Ф/К) 1. Понятия градуса,
градусной меры угла, развернутого и прямого углов были введены еще в 5
классе. Викторина: 1) Единица измерения углов. (Градус.) 2) Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле. (Градусная мера угла.) 3) 4) 5) 6) Градусная мера развернутого угла. (180°.) 7) Градусная мера прямого угла. (90°.) 8) Градусная мера неразвернутого угла. (Меньше 180°.) 9) Угол, градусная мера которого меньше 90°. (Острый.) 10) Угол, градусная мера которого больше 90°, но меньше 180°. (Тупой.) После того, как проверены ответы на вопросы викторины, можно перейти к рассмотрению свойств: • Равные углы имеют равные градусные меры. • Меньший угол имеет меньшую градусную меру. • Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов (рис. 34 учебника на с. 19). 2. Выполнение практических заданий № 41, 42, 43. 3. Решение задач № 45, 46 (устно). 4. Введение понятий прямого, острого и тупого углов с помощью рис. 35. 5. Решение задач № 51 (по рис. 38), 52 (по рис. 39) и 53 (устно) |
||
|
III этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решить задачи № 47 и 48. Решение записывается на доске и в тетрадях (объясняет учитель). 2. Решить задачи обучающего характера на доске и в тетрадях (учащиеся с помощью учителя делают на доске чертеж, записывают, что дано и что нужно найти, учатся оформлять решение задачи): 1) Луч ВD делит развернутый угол АВС на два угла, разность градусных мер которых равна 46°. Найдите образовавшиеся углы. 2) Луч СК делит прямой угол ВСМ на два угла, один из которых в 4 раза больше другого. Найдите образовавшиеся углы. 3) Луч DО делит прямой угол АDВ на два угла, градусные меры которых относятся как 5 : 4. Найдите угол между лучом DО и биссектрисой угла АDВ |
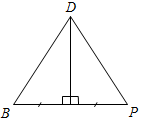
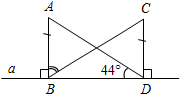
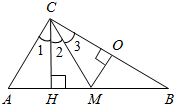
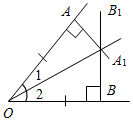
№ 47. Дано:ÐАОВ. а) ÐАОЕ = 44°, ÐЕОВ = 77°. б) ÐАОЕ = 12°37¢, ÐЕОВ = 108°25¢. Найти:ÐАОВ.
Рис. 1 Решение: а) ÐАОВ = ÐАОЕ + ÐЕОВ(свойство измерения углов). ÐАОВ = 44° + 77° ÐАОВ = 121° б) ÐАОВ = ÐАОЕ + ÐЕОВ ÐАОВ = 12°37¢ + 108°25¢ ÐАОВ = 120°62¢ = 121°02¢, так как 60¢ = 1°. Ответ: а) 121°; б) 121°02¢. № 48. Дано:ÐАОВ = 78°, ÐАОС меньше ÐВОС на 18°. Найти:ÐСОВ.
Рис. 2 Решение: Примем ÐАОС = х, следовательно, ÐСОВ = х + 18. Так как ÐАОВ = ÐАОС + ÐСОВ, то: 78 = х + х + 18 78 = 2х + 18 2х = 60 ÐАОС = 30°, ÐСОВ = 48°. Ответ: 48° |
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Составьте четверостишие с использованием слов «угол», «биссектриса», «градус», «развернутый угол», «прямой угол» |
(И) Домашнее задание: изучить пункты 9 и 10 (самостоятельно); ответить на вопросы 14–16 на с. 25–26; выполнить практическое задание № 44; решить задачи № 49, 50, 52 |
||
Урок7. Смежные и вертикальные углы
|
Цель деятельности |
Создать условия для введения понятий смежных и вертикальных углов, рассмотрения их свойств, введения понятия перпендикулярных прямых и демонстрации применения этих понятий при решении задач |
|
|
Термины и понятия |
Угол, смежные углы, вертикальные углы, перпендикулярные прямые |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления |
Познавательные: выдвигают гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); парная (П) |
|
|
Образовательные |
• Задания для самостоятельной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Систематизировать |
(И) Самостоятельная тестовая работа с последующей самопроверкой (см. Ресурсный материал) |
|
|
II этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Ввести понятия смежных углов, вертикальных углов и перпендикулярных прямых |
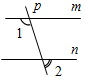
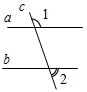
(Ф) 1. Ввести понятие смежных углов и ознакомить учащихся с их свойством: сумма смежных углов равна 180°. 2. Выполнить практическое задание № 55 (на доске и в тетрадях). 3. Решить задачи № 58, 59, 60, 63, 62 (по рис. 46 на с. 24) (устно). 4. Решить задачу № 61 (в, г) (письменно). Решение записывает на доске учитель. 5. Понятие вертикальных углов можно ввести во время выполнения следующего задания: – Начертите неразвернутый ÐАОВ и назовите лучи, являющиеся сторонами этого угла. – Проведите луч ОС, являющийся продолжением луча ОА, и луч ОD, являющийся продолжением луча ОВ. – Запишите в тетради: углы АОВ и СОD называются вертикальными. 6. Дать определение вертикальных углов (рис. 41 на с. 22). 7. Обоснование того факта, что вертикальные углы равны, вначале можно провести на конкретном примере, который фиксируется на доске и в тетрадях учащихся. Доказательство: ÐМОK + ÐDOM = 180°, так как ÐМОK и ÐDOM смежные и их сумма равна
180°, отсюда ÐМOK = ÐCOD + ÐDOM = 180°, так как ÐCOD и ÐDОM смежные и их сумма равна
180°, отсюда ÐCOD =
Рис. 1 Получили, что ÐМОK = 180° – ÐDОM и ÐCOD = 180° – ÐDOM, значит, ÐMOK = ÐCOD, а это вертикальные углы. Итак, вертикальные углы равны. 8. Решить задачу № 65 (устно). 9. Решить задачу № 67 по рис. 47 на с. 25 (устно). 10. Ввести понятие перпендикулярных прямых (рис. 42 на с. 22). 11. Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые. 12. Выполнить практическое задание № 57. 13. Провести беседу о построении прямых углов на местности (п. 13) |
|
|
III этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Отработать основные понятия при решении задач |
(Ф/И) Решить на доске и в тетрадях № 65 (а), 66 (а). (П) Решить № 64 (а), 66 (б), представить решение на доске и обсудить |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Оцените свою работу в парах и поставьте друг другу оценки. – Составьте синквейн к уроку |
(И) Домашнее задание:
изучить пункты 11–13 из § 6; ответить на вопросы 17–21 |
|
Ресурсный материал
Самостоятельная работа
Вариант I
1. Дано:ÐAOB = 122°, ÐAOD = 19°, ÐCOB = 23° (рис. 1).
Найти:ÐCOD.
а) 90°; б) 80°; в) 164°.
2. Дано: луч ОС проходит между сторонами угла АОВ, равного 120°.
Найти:ÐAOC, если ÐAOC меньше ÐСОВ в 2 раза.
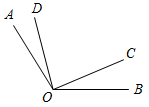
Рис. 1
а) 80°; б) 60°; в) 40°.
3. Может ли луч с проходить между сторонами угла ab, если Ðab = 130°, Ðac = 40°, Ðcb = 90°?
а) Да; б) нет; в) в условии не хватает данных.
Вариант II
1. Дано:ÐAOD = 22°, ÐDOC = 47°, ÐAOB = 132° (рис. 2).
Найти:ÐСОВ.
а) 63°; б) 53°; в) 157°.
2. Дано: луч ОС проходит между сторонами угла АОВ, равного 120°.
Найти:ÐСОВ, если ÐAOC на 30° больше ÐСОВ.
Рис. 2
а) 75°; б) 90°; в) 45°.
3. Может ли луч с проходить между сторонами Ðab, если Ðab = 50°, Ðac= 120°, Ðcb = 70°?
а) Да; б) нет; в) в условии не хватает данных.
Ответы:
|
№ |
Вариант I |
Вариант II |
|
1 |
б |
а |
|
2 |
в |
в |
|
3 |
а |
б |
Урок8. Перпендикулярные прямые
|
Цели деятельности |
Создать условия для повторения понятия перпендикулярных прямых, рассмотрения свойства перпендикулярных прямых; совершенствовать у учащихся умение решать задачи |
|
|
Термины и понятия |
Угол, смежные углы, вертикальные углы, перпендикулярные прямые |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
|
|
Образовательные |
• Чертежи к задачам. • Задания для парной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Выполнение задания: на каком рисунке изображены смежные углы?
а) б)
в) г) |
|
|
II этап. Решение задач по готовым чертежам |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
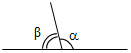
(П) Выполнение заданий и взаимопроверка. 1. Дано:a – β = 30°. 3. Дано: ОЕ – биссектриса ÐCOD; ÐDOE = 32°. Найти:a, β. Найти:ÐBOC, ÐAOF.
Рис. 1 Рис. 3 Ответ: a = 105°, β = 75°. Ответ: ÐBOC = 180° – ÐCOD = 116°; ÐAOF = ÐCOE = 32°. 2. Дано:ÐABD : ÐCBD = 1 : 5. 4. Дано:ÐАОВ = Найти:ÐAOB, ÐBOC.
Рис. 2 Рис. 4 Ответ: ÐABD = 30°, ÐCBD = 150°. Ответ: ÐAOB = |
|
|
III этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Ввести понятие перпендикулярных прямых |
(Ф/И) При изучении нового материала можно опираться на имеющиеся у учащихся знания по данной теме за курс математики 6 класса. – Какие прямые называются перпендикулярными? (Две прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла.) – Запишите, используя математические символы: «Прямая АВ перпендикулярна прямой CD». Выполните соответствующий рисунок и укажите все углы. – Пересекаются ли две прямые, перпендикулярные третьей? (Нет.) Учащиеся могут вспомнить, что такие прямые параллельны. – Две прямые, перпендикулярные третьей, не пересекаются – это свойство перпендикулярных прямых. Докажем это свойство (п. 12 учебника). (Доказывает учитель.) П. 13 «Построение прямых углов на местности» можно порекомендовать прочитать дома |
|
|
IV этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
(П) После выполнения заданий представить решение задач на доске. № 1. Два тупых угла имеют общую сторону, а две другие стороны взаимно перпендикулярны. Найдите величину тупых углов, если известно, что они равны. Решение: ÐAOB = ÐAOC. ВО^ОС, значит, ÐВОС = 90°. Так как ÐAOB = ÐAOC, то 2ÐАОВ = 360° – 90° = 270°, ÐАОВ = 135°.
Рис. 5 № 2. Из вершины развернутого угла проведены два луча, которые делят его на три равные части. Докажем, что биссектриса среднего угла перпендикулярна сторонам развернутого угла. Решение: ÐAOB = ÐВОС = ÐCOD = 60°. OK – биссектриса ÐВОС, тогда ÐCOK = ÐВОK = 30°, следовательно,
Рис. 6 № 3. Углы АОВ и DОС смежные, OМ – биссектриса ÐAOB, луч ON принадлежит внутренней области ÐВОС и перпендикулярен ОМ. Является ли ON биссектрисой ÐBOC? Почему?
Рис. 7 Решение: ÐAOB и ÐВОС смежные, значит, ÐAOB = 180° – ÐBOC, а так как ОМ –
биссектриса ÐАОВ, то ÐВОМ = |
|
|
V этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Оцените свою работу на
уроке и работу своих – Что нового узнали на уроке? |
(И) Домашнее задание: решить задачи № 66, 68 и дополнительные задачи. 1. Один из смежных углов составляет 0,2 другого. Найдите эти смежные углы. 2. Сумма трех углов, образовавшихся
при пересечении двух прямых, равна 325°. |
|
Урок9. Решение задач
|
Цели деятельности учителя |
Создать условия для повторения, закрепления материала главы I; совершенствовать навыки решения задач; подготовить учащихся к предстоящей контрольной работе |
|
|
Термины и понятия |
Угол, смежные углы, вертикальные углы, перпендикулярные прямые, биссектриса угла, луч, отрезок |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок: осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость изучения предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для самостоятельной работы. • Тест |
|
|
I этап. Актуализация знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить уровень сформированности теоретических знаний |
(Ф/И) Проверка домашнего задания. К доске вызываются двое учащихся. № 66. а) Если Ð2 + Ð4 = 220°, так как Ð2, Ð4 – вертикальные, то Ð2 = Ð4 = 220° : 2 = 110°. Ð1 = Ð3 = 70° (смежные с Ð2 и Ð4).
Рис. 1 Ответ: 70°, 110°, 70°, 110°. б) Если 3 · (Ð1 + Ð3) = Ð2 + Ð4, в) Если Ð2 – Ð1 = 30°. Примем Ð1 = х, следовательно: так как Ð1 = Ð3 = х, Ð2 = х + 30° то Ð2 = Ð4 = 180° – х подставим в условие: х + х + 30° = 180° 3 · (х + х) = 180° – х + 180° – х 2х = 150° 6х = 360° – 2х х = 75° 8х = 360° Ð1 = 75°, Ð2 = 105° х = 45° Ответ: 75°, 105°. Ð1 = Ð3 = 45°, Ð2 = Ð4 = 135° Ответ: 45°, 135°, 45°, 135°. № 68. Дано: ADÇBEÇFC = O, ÐAOB = 50°, ÐFOE = 70°. Найти:ÐАОС, ÐBOD, ÐCOE, ÐCOD.
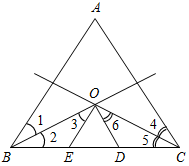
Рис. 2 Решение: 1) ÐEOD = ÐAOB = 50°. 2) ÐFOD = ÐFOE + ÐEOD = 70° + 50° = 120°. 3) ÐCOD = 180° – ÐFOD = 180° – 120° = 60°. 4) ÐAOB = 50° + 70° = 120°; ÐCOE = 60° + 50° = 110°; ÐBOD = 70° + 60° = 130°, ÐCOD = 60°. Ответ: 120°, 130°, 110°, 60° |
|
|
II этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Проверить уровень сформированности знаний при решении простейших задач |
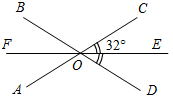
(И) Работа рассчитана на 10–15 минут. Далее осуществляется взаимопроверка. Вариант I 1. Смежные углы относятся как 1 : 2. Найдите эти смежные углы. 2. Один из углов, образовавшихся при пересечении двух прямых, равен 21°. Найдите остальные углы. 3. Дано:a = 30°, β = 140°. Найти:Ð1, Ð2, Ð3, Ð4.
Рис. 3 Вариант II 1. Один из смежных углов больше другого на 20°. Найдите эти смежные углы. 2. Один из углов, образовавшихся при пересечении двух прямых, равен 102°. Найдите остальные углы. 3. Дано:a = 20°, β = 130°. Найти:Ð1, Ð2, Ð3, Ð4.
Рис. 4 Решение: Вариант I 1. Так как Ð1 : Ð2 = 1 : 2, то Ð1 = х, Ð2 = 2х. Но Ð1 + Ð2 = 180°,тогда х + 2х = 180°, х = 60, значит, Ð1 = 60°, Ð2 = 120°.
Рис. 5 2. Пусть Ð1 = 21°, тогда Ð3 = Ð1, как вертикальные, и Ð3 = 21°. Ð1 и Ð2 – смежные и Ð1 + Ð2 = 180°. Тогда Ð2 = 180° – Ðl = 159°. Но Ð2 = Ð4, как вертикальные, значит, Ð4 = 159°.
Рис. 6 3. a = 30°, тогда Ð4 = 30°, так как Ð4 и угол с градусной мерой a – вертикальные. β = 140°, тогда Ð2 = 140°, так как Ð2 и угол с градусной мерой β – вертикальные. Ð2 + Ð3 + Ð4 = 180°, тогда Ð3 = 180° – (Ð2 + Ð4) = 10°. Ð3 и Ð1 – вертикальные, поэтому Ð3 = Ð1, Ð1 = 10°. Вариант II 1. Ð2 на 20° больше Ð1, тогда Ð1 = х, Ð2 = х + 20°. Но Ð1 + Ð2 = 180°, тогда х + х + 20° = 180°, х = 80°, значит, Ð1 = 80°, Ð2 = 100°.
Рис. 7 2. Пусть Ð1 = 102°, тогда Ð3 = Ð1, как вертикальные, и Ð3 = 102°. Ð1 и Ð2 – смежные и Ð1 + Ð2 = 180°, тогда Ð2 = 180° – Ð1 = 78°. Но Ð2 = Ð4, как вертикальные, значит, Ð4 = 78°.
Рис. 8 3. a = 20°, тогда Ð4 = 20°, так как Ð4 и угол с градусной мерой a – вертикальные. β = 130°, тогда Ð2 = 130°, так как Ð2 и угол с градусной мерой β – вертикальные. Ð2 + Ð3 + Ð4 = 180°, тогда Ð3 = 180° – (Ð2 + Ð4) = 30°. Ð3 и Ð1 – вертикальные, поэтому Ð3 = Ð1, Ð1 = 30° |
|
|
III этап. Тест |
||
|
Цель деятельности |
Тестовые задания |
|
|
Повторить теоретический материал |
(И) 1. Точка С лежит на луче АВ. Какая из точек А, В, С лежит между двумя другими? а) А; в) С; б) В или С; г) В. 2. Отрезок ХМ пересекает прямую а. Отрезок XD пересекает прямую а. Пересекает ли прямую а отрезок МD? а) Да; в) никогда не пересекает; б) может не пересекать; г) нет правильного ответа. 3. Один из углов, образованных при пересечении двух прямых, – прямой. Остальные углы… а) острые и прямой; в) прямые; б) тупые и прямой; г) нет правильного ответа. 4. Сумма двух углов, образованных при пересечении двух прямых, равна 180°. Эти углы… а) смежные; в) нет правильного ответа; б) вертикальные; г) могут быть смежными, могут быть вертикальными. 5. Если точка В принадлежит отрезку АС, то... а) АВ + ВС = АС; в) ВС + АС = АВ; б) АВ + АС = ВС; г) нет правильного ответа. 6. Если луч ОС проходит между сторонами угла АОВ, то... a) ÐAOC = ÐBOC; в) ÐAOB + ÐBOC = ÐAOC; б) ÐAOC + ÐBOC = ÐAOB; г) ÐAOC + ÐAOB = ÐBOC. 7. Если точка В – середина отрезка АС, то… а) АВ + ВС = АС; в) АВ = 2АС; б) АС = ВС; г) АС = 2АВ. 8. Если луч ОС – биссектриса ÐAOB, то… a) ÐAOB = ÐAOC + ÐBOC; в) ÐAOC = ÐBOC; б) ÐAOC = ÐAOB; г) ÐAOB ≠ ÐBOC. Ответы: 1 – б; 2 – г; 3 – в; 4 – г; 5 – а; 6 – б; 7 – г; 8 – в |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Оцените свою работу на уроке. – Какие понятия повторяли на уроке? |
(И) Домашнее задание: решить задачи № 74, 75, 80, 82 |
|
Урок10. Контрольная работа № 1
|
Цель деятельности учителя |
Создать условия для проверки знаний, умений навыков учащихся по теме «Измерение отрезков. Измерение углов. Смежные и вертикальные углы» |
|
|
Термины и понятия |
Угол, смежные углы, вертикальные углы, перпендикулярные прямые, биссектриса угла, луч, отрезок |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и контроль своей учебной деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают необходимость и важность изучения предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для контрольной работы |
|
|
I этап. Выполнение контрольной работы по вариантам |
||
|
Цель деятельности |
Задания для контрольной работы |
|
|
Проверить уровень знаний и умений по изученной теме |
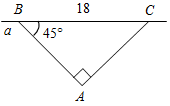
(И) Вариант I 1. Три точки В, С и D лежат на одной прямой. Известно, что ВD = 17 см, DС = 25 см. Какой может быть длина отрезка ВС? 2. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD. 3. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла. Вариант II 1. Три точки М, N и K лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МK? 2. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD. 3. С помощью транспортира начертите угол, равный 132°, и проведите биссектрису одного из смежных с ним углов. Вариант III (для более подготовленных учащихся) 1. Лежат ли точки M, N и P на одной прямой, если MP = 12 см, MN = 5 см, PN = 8 см? 2. Найдите неразвернутые углы, образованные при пересечении двух прямых, если разность двух из них равна 37°. 3. На рисунке АВ^СD, луч ОЕ – биссектриса угла АОD. Найдите угол СОЕ.
|
|
|
II этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Что выполняли на уроке? – Какие задания вызвали затруднения? Почему? – Как оцениваете свою работу на уроке? |
(И) Домашнее задание: повторить § 1–6 |
|
Урок11. Треугольник
|
Цели деятельности учителя |
Создать условия для введения понятий треугольника и его элементов, периметра треугольника, для обучения оформлению и решению задач; способствовать развитию логического мышления учащихся |
|||
|
Термины и понятия |
Треугольник, угол между двумя сторонами |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Задания для самостоятельной и фронтальной работы |
|||
|
I этап. Актуализация знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Провести анализ ошибок контрольной работы |
(Ф/И) 1. Сообщить результаты контрольной работы. 2. Прокомментировать основные ошибки. 3. Решить задачи, вызвавшие у учащихся наибольшие затруднения |
|||
|
II этап. Учебно-познавательная деятельность |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Повторить элементы треугольника |
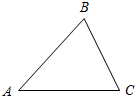
(Ф) При изучении темы необходимо учесть, что учащиеся имеют представление о треугольнике, его сторонах, углах и вершинах. Поэтому § 14 можно изучить в ходе выполнения следующих упражнений: 1. Начертите ∆ABC. Укажите: а) его стороны, вершины, углы; б) сторону, противолежащую ÐA, ÐВ, ÐС; в) между какими сторонами заключены ÐA, ÐВ, ÐС; г) углы, прилежащие стороне АВ, ВС, АС; д) угол, противолежащий стороне АВ, ВС, АС; е) периметр ∆АВС, если АВ = 5 см, ВС = 1 см, АС = 8 см; ж) формулу для вычисления периметра ∆АВС. 2. Решение задачи № 91 с оформлением на доске и в тетрадях учащихся. Дано:РАВС= 48 см, АС = 18 см, ВС – АВ = 4,6 см. Найти:АВ и ВС. Решение: Примем длину стороны АВ в сантиметрах за х, тогда ВС = (х + 4,6) см; 48 = АВ + АС + ВС = х + х + 4,6 + 18, отсюда: 2х = 25,4; х = 12,7. Значит, АВ = 12,7 см; ВС = 12,7 + 4,6 = 17,3 см. Ответ: 12,7 см и 17,3 см. 3. Сравнение треугольников. – Как выяснить, равны ли ∆АВС и ∆MNK? (Нужно ∆АВС наложить на ∆MNK; если они совместятся полностью, то ∆АВС= ∆MNK.) – Сравнение треугольников способом наложения – процесс не очень удобный. Нельзя ли каким-нибудь другим способом проверить, равны ли данные треугольники? (Нужно проверить, равны ли соответствующие элементы (стороны и углы) данных треугольников.) Записать на доске и в тетрадях: Если ∆ABC = ∆MNK, то АВ = MN, ВС = NK, АС = МK и ÐА = ÐM, ÐВ = ÐN, ÐC = ÐK |
|||
|
III этап. Закрепление изученной темы |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Научить решать задачи на применение изученного материала |
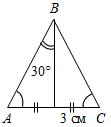
(И) 1. Учащиеся самостоятельно выполняют практическое задание № 89 (б, в). Учитель проверяет выполнение этого задания и исправляет ошибки. 2. Решение задачи № 90 (самостоятельно). 3. Решение задач (самостоятельно). 1) Дано: AB = AC = BC, AD = DC. 2) Дано: ∆ABD = ∆CBD, ÐFAB = 160°. РАВС = 36 см, РADC = 40 см. Найти:ÐBCD. Найти: стороны ∆ABC, ∆ADC.
Рис. 1 Рис. 2 Ответ: АВ = АС = ВС = 12 см, AD = DC = 14 см. Ответ: ÐBCD = 20° |
|||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Что повторили на уроке? – Что нового для себя открыли? |
(И) Домашнее задание: изучить п. 14 из § 1; ответить на вопросы 1 и 2 на с. 49; решить задачу № 156; выполнить практическое задание 89 (а) |
|||
Урок12. Первый признак равенства треугольников
|
Цель деятельности учителя |
Создать условия для разъяснения смысла слов «теорема» и «доказательство теоремы», формулировки и доказательства первого признака равенства треугольников |
|||
|
Термины и понятия |
Треугольник, угол между двумя сторонами, теорема, признак |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений |
Познавательные: выдвигают гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Задания для самостоятельной и фронтальной работы |
|||
|
I этап. Актуализация знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Систематизировать |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Повторение теории. 1) Повторить определение смежных углов и их свойство. 2) Повторить определение вертикальных углов и их свойство. 3) Вспомнить определение равных фигур, биссектрисы угла. 4) Вспомнить, какой угол называется острым, прямым, тупым. 5) Повторить определение треугольника, его элементов; определение периметра треугольника; определение равных треугольников |
|||
|
II этап. Мотивация к деятельности |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Совершенствовать навыки решения задач |
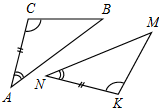
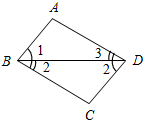
(И) 1. Дано: ∆АРС = ∆FMB, ÐP = ÐM, FB = 17 см, 2. Дано: ∆ABC = ∆ADC, ÐABC = 70°, ÐA = ÐF, PC = 23 см. AB = 10 см. Найти: AC, MB. Найти:ÐMDC, AD.
3. Дано: АВ = ВС = AC, AD = CD, РАВС = 36 м, РАDС = 40 см. Найти: стороны ∆ABC, ∆ADC.
Рис. 3 |
|||
|
III этап. Изучение новой темы |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Вывести первый признак равенства треугольников |
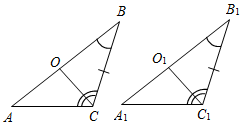
(Ф) Изучение темы осуществляется в форме беседы учителя с учащимися; теорему лучше доказать самому учителю. – Какие условия должны выполняться для
того, чтобы ∆АВС был равен ∆А1В1С1?
(АВ = А1В1, АС = А1С1, – Нельзя ли уменьшить количество условий для доказательства равенства двух треугольников? (Учащиеся высказывают свои предположения.) – Оказывается, не нужно проверять
равенство всех сторон и углов одного треугольника сторонам и углам другого
треугольника. Достаточно сравнить лишь три элемента одного треугольника с
тремя элементами другого. Сегодня мы изучим первый признак равенства треугольников, который гласит: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Это утверждение нам необходимо доказать. В математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы. – Какие теоремы нам уже известны? (Свойство смежных углов и свойство вертикальных углов.) – Любая теорема состоит из условия и заключения. Условие – это уже известные факты, о которых говорится в теореме, а заключение – это то, что нужно получить, доказать. – Выделите условие теоремы первого признака равенства треугольников. Выделите заключение. Итак, докажем первый признак равенства треугольников: Дано (условие): ∆ABC, ∆А1В1С1, АВ = А1В1, АС = А1С1, ÐA = ÐA1. Доказать (заключение): ∆АВС = ∆А1В1С1. Доказательство: см. п. 15 учебника. – Первый признак равенства треугольников удобнее называть признаком равенства треугольников по двум сторонам и углу между ними |
|||
|
IV этап. Решение задач |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Совершенствовать навыки в решении задач на изученную тему |
(Ф/И) 1. Найти пары равных треугольников:
Рис. 4 Рис. 5
Рис. 6 Рис. 7 2. Решить задачи № 96 и 97 на доске и в тетрадях |
|||
|
V этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Что нового узнали на уроке? – Что такое теорема? Из чего она состоит? |
(И) Домашнее задание: знать доказательство первого признака равенства треугольников (п. 15), решить задачи № 93, 94 и 95 |
|||
Урок13. Решение задач на применение первого признака
равенства треугольников
|
Цель деятельности |
Создать условия для совершенствования навыков решения задач на применение первого признака равенства треугольников, закрепления умения доказывать теоремы |
|||
|
Термины и понятия |
Треугольник, теорема, признак |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки; устанавливают причинно-следственные связи, строят логическое рассуждение, делают умозаключения. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Задания для фронтальной и самостоятельной работы |
|||
|
I этап. Актуализация знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Закрепить умение доказывать теорему |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Вызвать к доске учащегося для доказательства первого признака равенства треугольников. 3. Решить задачи по готовым чертежам (устно). 4. Найти равные треугольники:
Рис. 1 Рис. 2 Рис. 3 Рис. 4 |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Cовершенствовать навыки решения задач |
(Ф/И) 1. Решить задачу № 98 на доске и в тетрадях. 2. Решить задачи по готовым чертежам. Решение записать на доске и в тетрадях.
Рис. 5 Рис. 6 Рис. 7 |
|||
|
III этап. Самостоятельная работа |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Проверить уровень |
(И) Работа рассчитана на 10 минут. Решив ее, учащиеся сдают листки учителю. Вариант I Докажите равенство треугольников ADC и ABC, изображенных на рисунке, если AD = AB и Ð1 = Ð2. Найдите углы ADC и ACD, если ÐАВС = 108°, ÐАСВ = 32°.
Рис. 8 Вариант II Докажите равенство треугольников АВС
и ADC, изображенных на рисунке 53 учебника, если АВ = DC |
|||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Что повторили на уроке? – Оцените свою работу на уроке |
(И)Домашнее задание: решить № 97, 160 (а) |
|||
Урок14. Перпендикуляр к прямой.
Медианы, биссектрисы и высоты треугольника
|
Цель деятельности учителя |
Создать условия для введения понятий
перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника,
доказательства теоремы о перпендикуляре, обучения построению медианы,
биссектрисы и высоты |
|||
|
Термины и понятия |
Треугольник, медиана, биссектриса, высота, перпендикуляр |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют организовывать
учебное сотрудничество и совместную деятельность Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
|||
|
Образовательные |
• Задания для фронтальной работы |
|||
|
I этап. Актуализация знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить правильность выполнения |
(Ф/И) 1. Проверить правильность выполнения
домашнего задания. Для этого к доске вызываются двое учеников, 2. Проанализировать ошибки, допущенные в самостоятельной работе |
|||
|
II этап. Учебно-исследовательская деятельность |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Ввести понятия |
(Ф/И) 1. Выполнение практического задания (учитель это же задание выполняет на доске). – Начертите прямую а и отметьте точку А, не лежащую на прямой (рис. 1).
Рис. 1 – Через точку А проведите прямую, перпендикулярную прямой а. Точку пересечения прямых обозначьте Н. – Запишите в тетрадях: «Отрезок АН – перпендикуляр, проведенный из точки А к прямой а, если: 1) АН^а; 2) АÏа, НÎа». Теорема о перпендикуляре:Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и притом только один. Дано: а – прямая, точка АÏа. Доказать: 1) из точки А к прямой а можно провести перпендикуляр; 2) из точки А к прямой а можно провести единственный перпендикуляр. Доказательство: см. п. 16 учебника. 2. Определение: Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника. На доске и в тетрадях рисунок (рис. 2) и запись: AM – медиана ∆АВС, если МÎВС, ВМ = МС.
Рис. 2 – Начертите ∆MNK, постройте его медианы. (На доске это же задание выполняет один из учащихся по указанию учителя.) На доске и в тетрадях рисунок (рис. 3) и запись: MB, KA, NC – медианы ∆MNK. MBÇKAÇNC = О.
Рис. 3 3. Определение:Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. На доске и в тетрадях рисунок (рис. 4) и запись: BL – биссектриса ∆АВС, если LÎАС, ÐABL = ÐCBL.
Рис. 4 – Начертите ∆DEF,постройте его биссектрисы. (На доске это же задание выполняет один из учащихся по указанию учителя.) На доске и в тетрадях рисунок (рис. 5) и запись: DN, EK, FM – биссектрисы ∆DEF. DNÇЕKÇЕМ = О.
Рис. 5 4.Определение: Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника. На доске и в тетрадях рисунок (рис. 6) и запись: ВН – высота ∆АВС, если ВН^АС, НÎАС.
Рис. 6 – Начертите остроугольный, прямоугольный и тупоугольный треугольники и постройте их высоты.
Рис. 7 Рис. 8 Рис. 9 (К доске вызвать трех учеников, первый из них строит высоты для остроугольного треугольника, второй – для прямоугольного, третий – для тупоугольного.) |
|||
|
III этап. Решение задач на закрепление изученного материала |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать навыки построения медиан, биссектрис и высот |
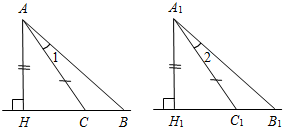
(П) Выполнить в парах (Ф/И) Выполнить на доске
|
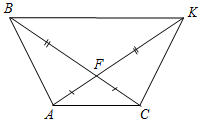
№ 105. Дано: А, С по одну сторону от а, АВ^а, CD^a, AB = CD, ÐADB = 44°. Доказать:ÐABD = ÐCDB. Найти:ÐАВС.
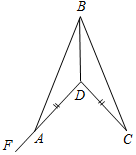
Рис. 10 Доказательство: 1) В DABD и DCDBBD – общая, AB = CD (по усл.). ÐВ = ÐD = 90° (так как АВ^а, CD^a). Таким образом, DABD = DCDB (по двум сторонам и углу между ними). 2) Из п. 1 следует, что ÐСВD = ÐADB = 44°, тогда ÐАВС = ÐABD – ÐCBD, ÐАВС = 90° – 44° = 46°. № 106. Дано: DАВС, AD – медиана, AD = DЕ, ÐAСD = 56°, ÐABD = 40°. Доказать:DABD = DЕCD. Найти:ÐАСЕ.
Рис. 11 Доказательство: 1) Рассмотрим DABD и DЕCD. BD = DC (по усл.), AD = DE (по усл.), Ð1 = Ð2 – вертикальные, DABD = DЕCD (по двум сторонам и углу между ними), тогда ÐABD = ÐЕCD (по определению равных треугольников), ÐЕCD = 40°. 2) ÐАСЕ = ÐAСD + ÐЕCD = 56° + 40° = 96° |
||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Какими свойствами обладают медианы, биссектрисы и высоты треугольника? – Составьте синквейн к уроку |
(И)Домашнее задание: изучить пункты 16 и
17; ответить на вопросы 5–9 на |
|||
Урок15. Свойства равнобедренного треугольника
|
Цель деятельности учителя |
Создать условия для введения понятий равнобедренного треугольника, равностороннего треугольника, рас-смотрения свойств равнобедренного треугольника и демонстрации их применения на практике |
||
|
Термины и понятия |
Равнобедренный треугольник, равносторонний треугольник, боковые стороны, основание, углы при основании |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение; понимают и используют математические средства наглядности. Регулятивные: осознают и принимают цели и задачи учебной деятельности. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||
|
Образовательные |
• Задания для самостоятельной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить правильность выполнения |
1. Обсуждение вопросов учащихся по домашнему заданию. 2. Теоретический опрос учащихся. 3. Самостоятельное решение тестовых заданий с последующей самопроверкой: 1) Дано: АО – медиана ∆АВС, АО = ОK, АВ = 6,3 см, ВС = 6,5 см, АС = 6,7 см. Найти: СK.
Рис. 1 а) 6,4 см; б) 6,7 см; в) 6,5 см; г) 6,3 см. 2) Дано: ОН и ON – высоты ∆МОK и ∆EOF, OH = ON, EN = 7,8 см, ОЕ = 8,6 см, НМ = 6,3 см.
Рис. 2 а) 13,9 см; б) 14,1 см; в) 14,9 см; г) 16,4 см. 3) В треугольниках ABC и KРМ проведены биссектрисы ВО и РЕ, причем ∆АВО = ∆KРЕ. Найдите отрезок ЕМ, если АС = 9 см, а ЕМ больше KЕ на 3,8 см. а) 6,4 см; б) 5,4 см; в) 2,6 см; г) 4,8 см. Ответы: 1 – г; 2 – б; 3 – а |
||
|
II этап. Учебно-познавательная деятельность |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ввести понятия равнобедренного и равносто-роннего
треугольников, дать представления |
(Ф/И) 1.Понятия равнобедренного и равностороннего треугольников.
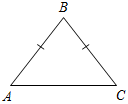
На доске и в тетрадях учащихся – рисунок и запись: ∆АВС – равнобедренный, так как АВ = ВС; АВ, ВС – боковые стороны равнобедренного ∆АВС; АС – основание равнобедренного ∆АВС; ÐA, ÐC – углы при основании равнобедренного ∆ABC; ÐB – угол при вершине равнобедренного ∆АВС.
Рис. 3 Определение:Треугольник, все стороны которого равны, называется равносторонним.
Теорема:В равнобедренном треугольнике углы при основании равны. Дано: ∆АВС, АВ = ВС. Доказать:ÐA = ÐC.
Рис. 4 Доказательство: Проведем биссектрису из вершины В к основанию АС.(Далее можно предложить учащимся продолжить доказательство самостоятельно, заслушать варианты, обсудить и записать в кратком виде ход доказательства.) (Г) 3. Свойство биссектрисы, проведенной к основанию равнобедренного треугольника. Можно предложить учащимся вывести это свойство самостоятельно, поставив перед ними проблему: «Как известно, биссектриса треугольника делит его угол пополам. Но в равнобедренном треугольнике биссектриса, проведенная к основанию, обладает еще одним очень важным свойством. В чем заключается это свойство?» Работа проводится в группах по 3–4 человека с последующим обсуждением этого свойства с доказательством. При обсуждении важно затронуть вопросы: – Каждая ли биссектриса равнобедренного треугольника является его высотой и медианой? – Является ли высота равнобедренного треугольника его биссектрисой и медианой? Если да, то какая из трех? |
||
|
III этап. Творческое задание |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Способствовать исследованию свойств медиан и высот равнобедренного треугольника в ходе выполнения заданий творческого характера |
(И) Вариант I Исследуйте медианы равнобедренного треугольника и перечислите все их особенности и свойства. Вариант II Исследуйте высоты равнобедренного треугольника и перечислите все их особенности и свойства. Далее проходит обсуждение свойств медианы и высоты равнобедренного треугольника |
||
|
IV этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать |
(Ф/И) 1. Решить задачи № 108 и 112 на доске и в тетрадях. 2. Решить № 116 (устно). 3. Решить задачу (устно). В равнобедренном треугольнике сумма всех углов равна 180º. Найдите углы этого треугольника, если известно, что: а) один из них равен 105º; б) один из них равен 38º (рассмотреть два случая) |
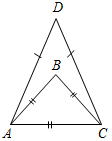
№ 108. Дано:DАВС, АВ = АС, РАВС = 40 см, DВСD, DB = DC = BC, PВCD = 45 см. Найти:ав и ВС.
Рис. 5 Решение: 1) РАВС = АВ + ВС + АС = ВС + 2АВ (так как DАВС равнобедренный),
2) PВCD = DB + ВС + CD = 3ВС (так как DDВС равносторонний), 45 = 3ВС, тогда ВС = 15 см. 40 = 15 + 2АВ. 2АВ = 25, тогда АВ = 12,5 см. Ответ: 12,5 см; ВС = 15 см.
Дано: АВ = ВС, Ð1 = 130°. Найти:Ð2.
Рис. 6 Решение: 1) Ð1 и ÐАСВ – смежные, значит, Ð1 + ÐАСВ = 180°, 2) Так как DАВС – равнобедренный, АВ = ВС
(по усл.), 3) Так как Ð2 = ÐВАС, как вертикальные, Ð2 = 50°. Ответ: 50° |
|
|
V этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Что узнали об углах равнобедренного треугольника? Равностороннего треугольника? – Перечислите свойства равнобедренного и равностороннего треугольников. – Задайте три вопроса по теме урока |
(И) Домашнее задание: изучить п. 18 с
доказательством теоремы на вопросы 10–12 на с. 50; решить задачи № 104, 107 и 117 |
||
Урок16. Свойства равнобедренного треугольника
|
Цели деятельности учителя |
Создать условия для закрепления теоретических знаний по изучаемой теме; совершенствовать навыки доказательства теорем, решения задач |
||
|
Термины и понятия |
Равнобедренный треугольник, равносторонний треугольник, боковые стороны, основание, углы при основании |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; устанавливают причинно-следственные связи, строят логическое рассуждение, умозаключение; понимают и используют математические средства наглядности. Регулятивные: принимают и сохраняют учебные задачи. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные |
• Задания для самостоятельной работы. • Чертежи к задачам |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить уровень |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Один учащийся на доске готовит доказательство теоремы о свойстве углов при основании равнобедренного треугольника. 3. Второй учащийся решает на доске задачу № 117 (по рис. 67). 4. Устно по готовым чертежам на доске учащиеся решают задачи. – Найдите ÐDВА.
Рис. 1 Рис. 2 Рис. 3 5. Теоретический тест (с последующей самопроверкой). (Ответы учащиеся записывают на двух листках, один из них сдают на проверку учителю, по другому проверяют правильность своих ответов. Ответы к тесту учитель записывает на доске после того, как учащиеся сдали работы.) 1) Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 2) Если треугольник равносторонний, то: а) он равнобедренный; б) все его углы равны; в) любая его высота является биссектрисой и медианой. 3) В каком треугольнике только одна его высота делит треугольник на два равных треугольника? а) В любом; б) в равнобедренном; в) в равностороннем. 4) Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 5) Если треугольник равнобедренный, то: а) он равносторонний; б) любая его медиана является биссектрисой и высотой; в) ответы а) и б) неверны. 6) В каком треугольнике любая его высота делит треугольник на два равных треугольника? а) В любом; б) в равнобедренном; в) в равностороннем. Ответы: 1 – б; 2 – а, б, в; 3 – б; 4 – а; 5 – в; 6 – в |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать |
(Ф/И) 1. Решение задач по готовым чертежам. Найти угол DВА.
Рис. 4 Рис. 5 Рис. 6 Рис. 7
Рис. 8 2. Решение № 119 и 120 (а) на доске и в тетрадях. 3. Самостоятельная работа на 10 минут. 1) Периметр равнобедренного треугольника 48 см, боковая сторона – 15 см. Найти основание треугольника. 2) Периметр равнобедренного треугольника равен 37 см. Основание меньше боковой стороны на 5 см. Найдите стороны этого треугольника |
||
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Оцените свою работу на уроке. – Закончите фразы: • Я научился… • У меня получилось… • Я смог… • Я попробую… |
(И) Домашнее задание: решить № 114, 118, 120 (б) |
||
Урок17. Второй признак равенства треугольников
|
Цели деятельности |
Создать условия для повторения и закрепления изученного ранее материала, изучения второго признака равенства треугольников и выработки навыков использования первого и второго признаков равенства треугольников при решении задач; способствовать развитию логического мышления учащихся |
||
|
Термины и понятия |
Треугольник, прилежащие углы |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию) |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют
организовывать учебное сотрудничество и совместную деятельность Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные |
• Чертежи к задачам. • Задания для фронтальной и индивидуальной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать навык решения задач по готовым чертежам с целью повторения первого признака равенства треугольников |
(Ф/И) 1. Проверка домашнего задания. 2. Решение задач (устно). 1) На рис. 1 DЕ = DK, Ð1 =Ð2. Найдите ЕС,ÐDСK и ÐDKС, если KС = 1,8 дм; ÐDСЕ = 45º,ÐDЕС =115º.
Рис. 1 2) ОВ = ОС, АО = DО; ÐАСВ = 42º, ÐDСF = 68º. Найдите ÐАВС.
Рис. 2 |
||
|
II этап. Изучение нового материала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Организовать выполнение
практической работы с целью подготовки к восприятию новой |
(Ф/И) Практическая работа. Начертите DMNK – такой, что ∆MNK = ∆ABC, если известно, что АВ = 4 см, ÐA = 54°, ÐВ = 46°. Построение: 1) отложить отрезок MN = 4 см, так как ∆MNK = ∆АВС, а значит, MN = AB; 2) построить ÐNMP = 54°; 3) построить ÐMNE = 46° по ту же сторону от прямой MN, что и ÐNMP; 4) МРÇNE = K, ∆MNK – искомый. (Идет обсуждение практического задания. Учитель задает вопросы, учащиеся отвечают на них.) – Будут ли равны ∆АВС и ∆MNK, если АВ = MN, ÐA = ÐM, ÐB = ÐN? (Да, ∆ABC = ∆MNK.) – Докажите равенство треугольников ABC и MNK. Дано: ∆ABC, ∆MNK, AB = MN, ÐA = ÐM, ÐB = ÐN. Доказать: ∆ABC = ∆MNK. Доказательство: Наложим ∆ABC на
∆MNK так, чтобы АВ совместилось с MN, а вершины С
и K лежали по одну сторону от MN. Так как по условию задачи АВ
= MN, то вершина А совместится с вершиной М, а вершина В
– с вершиной N. Луч АС совместится с лучом МK, так как ÐA = ÐМ, а луч ВС
совместится с лучом NK, так как ÐB = ÐN. – Итак, мы только что доказали второй признак равенства треугольников. Сформулируйте его и дайте ему название. Определение: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. – Второй признак равенства
треугольников можно назвать признаком равенства треугольников по стороне |
||
|
III этап. Решение задач на закрепление изученного материала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать навыки решения задач по изученной теме |
(Ф/И) 1. Решить задачи по готовым чертежам (устно).
Рис. 3 Рис. 4 Рис. 5
Рис. 6 Рис. 7 1) На рис. 3 Ð1 = Ð2 и Ð3 = Ð4. Докажите, что ∆АВС = ∆АDС. 2) На рис. 4 АС = СВ, ÐА = ÐВ. Докажите, что ∆ВСD = ∆АСЕ. 3) На рис. 5 АD – биссектриса угла ВАС, Ð1 = Ð2. Докажите, что ∆АВD = ∆АСD. 4) На рис. 6 ВО = ОС, Ð1 = Ð2. Укажите равные треугольники на этом рисунке. 5) На рис. 7 Ð1 = Ð2, ÐСАВ = ÐDВА. Укажите равные треугольники на этом рисунке. 2. Решить задачу № 121 (самостоятельно). 3. Решить задачу № 126 (по рис. 74 учебника на с. 40). 4. Решить задачу № 127 (записать решение этой более сложной задачи на доске и в тетрадях).
№ 127. Дано:DАВС, DА1В1С1, АВ = А1В1, ВС = В1С1, ÐВ = ÐВ1; DÎAB, D1ÎA1B1, ÐACD = ÐA1C1D1. Доказать:DBCD = DB1C1D1. Доказательство: 1) Рассмотрим DАВС и DА1В1С1: АВ = А1В1 (по
усл.), ВС = В1С1 (по усл.), ÐВ = ÐВ1 (по усл.), DАВС = DА1В1С1
Рис. 8 2) Рассмотрим DBCD и DB1C1D1, ВС = В1С1, ÐBCD = ÐB1C1D1 (так как ÐBCD = ÐС – ÐACD, ÐB1C1D1 = ÐВ = ÐВ1 (по усл.). DBCD = DB1C1D1 (по стороне и двум прилежащим углам), что и требовалось доказать |
||
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Что нового узнали на уроке? – Кто может повторить второй признак равенства треугольников? – Составьте синквейн по теме урока |
(И) Домашнее задание:
выучить доказательство теоремы из п. 19; решить задачи |
||
Урок18. Второй признак равенства треугольников
|
Цель деятельности учителя |
Совершенствовать навыки решения задач на применение второго признака равенства треугольников |
|||
|
Термины и понятия |
Треугольник, прилежащие углы |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию) |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: осознают важность и необходимость изучения предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|||
|
Образовательные |
• Тестовые задания |
|||
|
I этап. Актуализация опорных заданий учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить теоретический уровень усвоения материала |
(И) 1. Доказательство второго признака равенства треугольников. (К доске вызывается один из учащихся, ответ его заслушивается всем классом.) (Ф) 2. Фронтальная работа с классом – тестовые задания обучающего характера с последующей самопроверкой. 1) Для доказательства равенства треугольников ABC и MNK достаточно доказать, что: a) AC = MN; б) ÐC = ÐN; в) ВС = NK.
Рис. 1 2) Для доказательства равенства треугольников ABC и EDF достаточно доказать, что: a) AC = FE; б) ÐC = ÐE; в) ÐA = ÐF.
Рис. 2 3) Чтобы доказать равенство равносторонних треугольников ABC и MNK, достаточно доказать, что: a) ÐA = ÐM; б) AB = MN; в) РАВС = РMNK. 4) Чтобы доказать равенство двух равнобедренных треугольников TOS и DEF c основаниями TS и DF соответственно, достаточно доказать, что: a) ÐO = ÐE; б) TS = DF и ÐT = ÐD; в) TS = DF. 5) Выберите верное утверждение: a) BC = KМ; б) AB = KN; в) BC = NM.
Рис. 3 Ответы: 1 – в; 2 – б; 3 – б; 4 – б; 5 – а |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать |
(Г) Организует деятельность учащихся. Учащиеся распределяются в группы по 3–4
чело-века и решают задачи Учитель контролирует правильность
решения задач в группах, при необходимости консультирует как целые группы,
так Группы презентуют свои решения |
№ 130. Дано:DАВС и DА1В1С1, СО, С1О1 – медианы, ВС = В1С1, ÐВ = ÐВ1, ÐС = ÐС1. Доказать: 1) DАСО = DА1С1О1; 2) DВСО = DВ1С1О1.
Рис. 4 Доказательство: 1) Рассмотрим DАВС и DА1В1С1. ВС = В1С1 (по
усл.), ÐВ = ÐВ1 (по усл.), DАВС = DА1В1С1 (по сторонам и двум
углам). АВ = А1В1, ÐА = ÐА1, АС = А1С1 2) Рассмотрим DАОС = DА1О1С1. АС = А1С1 (из п. 1), ÐА = ÐА1 (из п. 1). АО = А1С1 DАОС = DА1О1С1 (по двум сторонам и углу между ними). 3) Рассмотрим DВСО = DВ1С1О1. ВС = В1С1 (по
усл.), ÐВ = ÐВ1 (по усл.), DВСО = DВ1С1О1 (по двум сторонам и углу между ними). № 131. Дано:DDEF и DMNP, EF = NP,
DF = MP, ÐF = ÐP, EE1, DD1
– биссектрисы, Доказать:ÐDOE = ÐMKN.
Рис. 5 Доказательство: 1) Рассмотрим DDEF и DMNP. EF = NP (по усл.), DF = MP (по
усл.),ÐF = ÐP 2) Рассмотрим DDOE и DMNK. DE = MN (из п. 1), ÐEDO = ÐNMK ÐDEO = ÐMNK DDOE = DMKN (по стороне и двум
прилежащим углам), тогда ÐDOE = ÐMKN № 133. Дано:DАВС, BD – биссектриса. Доказать:DАВС – равнобедренный.
Рис. 6 Доказательство: Рассмотрим DABD и DCBD: BD – общая, Ð1 = Ð2 (так как BD
– биссектриса), DABD = DCBD (по стороне и двум прилежащим углам). АВ = ВС (по определению равных треугольников), значит, DАВС – равнобедренный |
||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Оцените свою работу. – Оцените работу в группе |
(И) Домашнее задание: решить 129, 132, 134 |
|||
Урок18. Второй признак равенства треугольников
|
Цель деятельности учителя |
Совершенствовать навыки решения задач на применение второго признака равенства треугольников |
|||
|
Термины и понятия |
Треугольник, прилежащие углы |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию) |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: осознают важность и необходимость изучения предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|||
|
Образовательные |
• Тестовые задания |
|||
|
I этап. Актуализация опорных заданий учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить теоретический уровень усвоения материала |
(И) 1. Доказательство второго признака равенства треугольников. (К доске вызывается один из учащихся, ответ его заслушивается всем классом.) (Ф) 2. Фронтальная работа с классом – тестовые задания обучающего характера с последующей самопроверкой. 1) Для доказательства равенства треугольников ABC и MNK достаточно доказать, что: a) AC = MN; б) ÐC = ÐN; в) ВС = NK.
Рис. 1 2) Для доказательства равенства треугольников ABC и EDF достаточно доказать, что: a) AC = FE; б) ÐC = ÐE; в) ÐA = ÐF.
Рис. 2 3) Чтобы доказать равенство равносторонних треугольников ABC и MNK, достаточно доказать, что: a) ÐA = ÐM; б) AB = MN; в) РАВС = РMNK. 4) Чтобы доказать равенство двух равнобедренных треугольников TOS и DEF c основаниями TS и DF соответственно, достаточно доказать, что: a) ÐO = ÐE; б) TS = DF и ÐT = ÐD; в) TS = DF. 5) Выберите верное утверждение: a) BC = KМ; б) AB = KN; в) BC = NM.
Рис. 3 Ответы: 1 – в; 2 – б; 3 – б; 4 – б; 5 – а |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать |
(Г) Организует деятельность учащихся. Учащиеся распределяются в группы по 3–4
чело-века и решают задачи Учитель контролирует правильность
решения задач в группах, при необходимости консультирует как целые группы,
так Группы презентуют свои решения |
№ 130. Дано:DАВС и DА1В1С1, СО, С1О1 – медианы, ВС = В1С1, ÐВ = ÐВ1, ÐС = ÐС1. Доказать: 1) DАСО = DА1С1О1; 2) DВСО = DВ1С1О1.
Рис. 4 Доказательство: 1) Рассмотрим DАВС и DА1В1С1. ВС = В1С1 (по
усл.), ÐВ = ÐВ1 (по усл.), DАВС = DА1В1С1 (по сторонам и двум
углам). АВ = А1В1, ÐА = ÐА1, АС = А1С1 2) Рассмотрим DАОС = DА1О1С1. АС = А1С1 (из п. 1), ÐА = ÐА1 (из п. 1). АО = А1С1 DАОС = DА1О1С1 (по двум сторонам и углу между ними). 3) Рассмотрим DВСО = DВ1С1О1. ВС = В1С1 (по
усл.), ÐВ = ÐВ1 (по усл.), DВСО = DВ1С1О1 (по двум сторонам и углу между ними). № 131. Дано:DDEF и DMNP, EF = NP,
DF = MP, ÐF = ÐP, EE1, DD1
– биссектрисы, Доказать:ÐDOE = ÐMKN.
Рис. 5 Доказательство: 1) Рассмотрим DDEF и DMNP. EF = NP (по усл.), DF = MP (по
усл.),ÐF = ÐP 2) Рассмотрим DDOE и DMNK. DE = MN (из п. 1), ÐEDO = ÐNMK ÐDEO = ÐMNK DDOE = DMKN (по стороне и двум
прилежащим углам), тогда ÐDOE = ÐMKN № 133. Дано:DАВС, BD – биссектриса. Доказать:DАВС – равнобедренный.
Рис. 6 Доказательство: Рассмотрим DABD и DCBD: BD – общая, Ð1 = Ð2 (так как BD
– биссектриса), DABD = DCBD (по стороне и двум прилежащим углам). АВ = ВС (по определению равных треугольников), значит, DАВС – равнобедренный |
||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Оцените свою работу. – Оцените работу в группе |
(И) Домашнее задание: решить 129, 132, 134 |
|||
Урок19. Третий признак равенства треугольников
|
Цель деятельности |
Создать условия для изучения третьего признака равенства треугольников и его закрепления в ходе решения задач, отработки у учащихся умения применять изученные теоремы при решении задач |
|||
|
Термины и понятия |
Треугольник, углы, стороны |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию) |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Задания для фронтальной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить уровень |
(Ф/И) 1. Проверить домашнее задание. Для этого можно к доске вызвать троих учащихся. 2. У доски доказать второй признак равенства треугольников |
|||
|
II этап. Изучение новой темы |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Доказать третий признак равенства треугольников |
(Ф) Учитель сам читает формулировку третьего признака равенства треугольников и доказывает его до рассмотрения первого случая. Доказательство первого случая можно провести в виде беседы с учащимися. Третий признак равенства треугольников: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Дано: ∆ABC, ∆А1В1С1, АВ = А1В1, ВС = В1С1, АС = А1С1. Доказать: ∆АВС = ∆А1В1С1.
Рис. 1 Рис. 2 Рис. 3 Рис. 4 Доказательство: Приложим ∆АВС к DА1В1С1 (см. рис. 1), так чтобы сторона АВ совместилась со стороной А1В1 (они совместятся, так как по условию теоремы АВ = А1В1), а вершины С и С1, находились по разные стороны от прямой А1В1. Возможны три случая: 1) луч СС1 проходит внутри угла (рис. 2); 2) луч СС1 совпадает с одной из сторон угла В1С1А1(рис. 3); 3) луч СС1 проходит вне угла В1С1А1(рис. 4). Докажем первый случай. – Что вы можете сказать о треугольниках С1А1С и С1В1С? (Они равнобедренные.) – Равны ли углы А1С1В1
и АСВ? Почему? (ÐА1С1В1 = ÐАСВ, так как ÐА1С1В1 = ÐA1C1C + ÐB1C1C, ÐACB = – Равны ли ∆АВС и ∆А1В1С1?
(∆АВС = ∆А1В1С1
по двум сторонам и углу между ними, так как АС = А1С1,
– Итак, ∆АВС = ∆А1В1С1. Далее можно предложить учащимся доказать равенство треугольниковАВСиА1В1С1во втором или третьем случае, а оставшийся случай рассмотреть дома. Доказательство второго случая. ∆В1С1С – равнобедренный с основанием СС1, так как В1С1 = ВС = В1С по условию теоремы. В1А1 – медиана ∆В1С1С, так как С1А1 = АС по условию теоремы, а АС = А1С. Медиана, проведенная к основанию равнобедренного треугольника, является его биссектрисой, то есть ÐС1В1А1 = ÐСВА. ∆АВС = ∆А1В1С1
по двум сторонам и углу между ними (АВ = А1В1,
ВС = В1С1 по условию теоремы, ÐСАВ = Доказательство третьего случая. ∆В1С1С
– равнобедренный с основанием СС1, так как В1С1
= ВС по условию теоремы. ÐB1C1C = ÐВСС1, как углы при
основании равнобедренного треугольника. ∆А1С1С
– равнобедренный с основанием СС1, так как ÐВ1С1А1 = ÐВСА, так как ÐВ1С1А1 = ÐB1C1C – ÐA1C1C, ÐBCA = ÐBCC1 – ÐACC1, a ÐB1C1C = ÐBCC1 ∆ABC = ∆A1B1С, по двум сторонам и углу между ними (ВС = В1С1, АС = A1C1, ÐВСА = ÐB1C1A1). Далее можно ввести понятие жесткой
фигуры или предложить учащимся самостоятельно прочитать |
|||
|
III этап. Решение задач на закрепление изученной темы |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
На простых задачах отработать применение третьего признака равенства треугольников |
(Ф/И) 1. Найдите пары равных треугольников и докажите их равенство.
Рис. 5 Рис. 6 Рис. 7
Рис. 8 Рис. 9 Рис. 10 2. Решить № 135 (устно). 3. Решить № 138 на доске и в тетрадях |
|||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – С чем познакомились на уроке? – Задайте три вопроса по теме урока |
(И) Домашнее задание: повторить п. 15–19, изучить п. 20; решить № 134, 136, 137 |
|||
Урок 20. Решение задач
|
Цели деятельности учителя |
Создать условия для организации и проведения повторения и закрепления изученного материала в ходе решения задач, обучения учащихся умению применять изученные теоремы при решении задач; способствовать развитию логического мышления |
|||
|
Термины и понятия |
Треугольник, углы, стороны, признаки равенства |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию) |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Задания для самостоятельной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Задание для контрольной работы |
|||
|
Систематизировать |
(Ф/И) 1. Проверка выполнения домашнего задания. 2. Теоретический опрос. 3. Самостоятельная работа на 10–15 минут
(см. Ресурсный материал). Учащиеся решают работу на листках |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать |
(Ф/И) 1. Организовать решение № 139 2. Организовать решение № 169 Рассказать учащимся о способе измерения
ширины озера(отрезка АВ) по заранее изготовленной таблице: «Чтобы
измерить на местности расстояние между двумя точками А и В, из
которых одна (точка А) недоступна, провешивают направление отрезка АВ
и на его продолжении отмеряют на земле произвольный отрезок ВС.
Выбирают на местности точку О, из которой видна точка А и можно
пройти к точкам В и С. Провешивают прямые ВОЕ и СОD,
отмеряют на местности DО = ОС и ОЕ = Тогда FE равно искомому расстоянию. Расстояние FE измеряют на земле с помощью рулетки». 3. Организовать решение задачи |
№ 139. Дано:АВ = CD, AD = BC, BE – биссектриса ÐАВС, DF – биссектриса DADC. Доказать: 1) ÐАВЕ = ÐADF; 2) DАВЕ = DCDF.
Рис. 1 Доказательство: 1) Рассмотрим DАВС и DCDA. АВ = CD (по усл.), BC = AD (по
усл.), 2) ÐАВЕ = ÐADF = 3) Рассмотрим DАВЕ и DСDF: АВ = CD (по усл.), ÐВАС = ÐDCA (из п. 1). Ð1 = Ð2 (из пп. 1 и 2), таким образом, DАВЕ = DСDF (по стороне и двум прилежащим углам). № 176. Дано:DАВС и DА1В1С1, АВ = А1В1,
АС = А1С1, АМ = А1М1;
АМ, А1М1 – Доказать:DАВС = DА1В1С1.
Рис. 2 Доказательство: 1) Сделаем дополнительное построение:
проведем АМ и А1М1 за точки 2) Рассмотрим DАМС и DBMD. AM = MD (по постр.), BM = MC (по усл.), Ð1 = Ð2 (вертик.), DАМС = DBMD (по двум сторонам и углу между ними), тогда АС = BD
(по определению равных треугольников), так как 3) Рассмотрим DABD и DA1B1D1. АВ = А1В1 (по усл.), AD = A1D1 (так как АМ = А1М1),
BD = B1D1 (из п. 2); таким
образом, DABD = DA1B1D1 Так как ВМ = B1M1, то ВС = В1С1 (ВС = 2ВМ; В1С1 =2B1М1). 4) Рассмотрим DАВС и DА1В1С1. АВ = А1В1 (по усл.), АС = А1С1 (по усл.), ВС = В1С1 (из п. 3). Таким образом, DАВС = DА1В1С1 (по трем сторонам), что и требовалось доказать |
||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Перечислите признаки равенства треугольников. – Поразмышляйте на тему «Как бы мы доказывали равенство треугольников, если бы не знали признаков их равенства?» |
(И) Домашнее задание: повторить пункты 16–20 из § 2 и 3; решить задачи № 140, 172. Дополнительная задача: Два равнобедренных треугольника АВС и ADC имеют общее основание АС. Вершины В и D расположены по разные стороны от АС. Точка Е лежит на отрезке BD, но не лежит на отрезке АС. Докажите, что ÐEAC = ÐАСЕ |
|||
Ресурсный материал
Самостоятельная работа
![]() Вариант I
Вариант I
1. Дано: АВ = CD, BC = DA, ÐС = 40°.
Доказать: ∆ABD = ∆CDB.
Найти:ÐA.
2. На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – медиана треугольника.
Докажите, что MD = ND.
Вариант II
![]() 1. Дано:AD = AB, CD = CB, ÐD = 120°.
1. Дано:AD = AB, CD = CB, ÐD = 120°.
Доказать: ∆DAC = ∆BAC.
Найти:ÐВ.
2. На боковых сторонах равнобедренного треугольника ABC отложены равные отрезки ВМ и BN. BD – высота треугольника.
Докажите, что MD = ND.
Урок 21. Задачи на построение. Окружность
|
Цель деятельности учителя |
Создать условия для систематизации знаний об окружности и ее элементах, для отработки навыков решения задач по данной теме |
||
|
Термины и понятия |
Окружность, центр, радиус, диаметр, хорда |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют формулировать определение окружности, объяснять, что такое центр, радиус, диаметр, хорда окружности |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные |
• Задания для теста |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить правильность выполнения домашнего задания |
(Ф/И) 1. Сообщить результаты самостоятельной работы. 2. Проверить правильность выполнения домашнего задания |
||
|
II этап. Учебно-познавательная деятельность |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Ввести понятия окружности и ее элементов |
(И) Понятие окружности и ее элементов вводится в курсе математики пятого класса, поэтому изучение нового материала можно организовать следующим образом: 1. Прочитать самостоятельно § 21. 2. Выполнить задания теста (см. Ресурсный материал). (На каждую парту раздаются листки с тестовым заданием. Учитель читает задание, учащиеся предлагают верный ответ.) |
||
|
III этап. Закрепление изученного материала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Отработать навыки решения задач по изученной теме |
(Ф/И) 1. Решить задачу № 143 (устно). 2. Решить задачу № 144 на доске и в тетрадях. 3. Решить задачу № 146 на доске и в тетрадях. 4. Решить задачу № 147 на доске и в тетрадях. Указание: рекомендовать
учащимся после изображения окружности начертить прямой угол с вершиной |
||
|
IV этап. Самостоятельная работа |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Проверить уровень усвоения теоретического материала и умения его применять при решении задач |
(И) Вариант I Отрезки KМ и ЕF являются диаметрами окружности с центром О. Докажите, что: а) ÐFEM = ÐKМЕ; б) отрезки KЕ и МF равны. Вариант II Отрезки МЕ и РK являются диаметрами окружности с центром О. Докажите, что: а) ÐEMР = ÐМРK; б) отрезки МK и РЕ равны. Вариант III В окружности с центром О проведены диаметр АС и радиус ОВ так, что хорда ВС равна радиусу. Найти ÐАОВ, если ÐВСО = 60°. Вариант IV В окружности с центром О проведены хорды АВ и СD. Докажите, что АВ = СD, если ÐАОС = ÐВОD |
||
|
V этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Дайте определение окружности. – Перечислите все элементы окружности. – Составьте синквейн к уроку |
(И) Домашнее задание: изучить п. 21 из § 4; ответить на вопрос 16 на с. 49; решить задачи № 145, 162; принести на следующий урок циркули и линейки. Дополнительная задача: АВ и CD – два диаметра окружности с центром в точке О. Луч ОЕ – биссектриса угла АОС. ОЕ пересекает окружность в точке K, причем KЕ = KО. Периметр треугольника KСО в три раза больше радиуса окружности. Докажите, что точки Е, А, С и О лежат на одной окружности |
||
Ресурсный материал
Тест
1) Вычеркнуть ненужные слова текста в скобках.
а) Окружность – это (абстрактная, геометрическая, плоская) фигура, состоящая из (множества, всех) точек, расположенных на (одинаковом, заданном) расстоянии от (некоторой, центральной) точки.
б) Радиусом окружности называется (линия, прямая, отрезок), соединяющая центр окружности с (заданной, какой-либо) точкой окружности.
2) Закончить определение: диаметр окружности – это...
а) два радиуса, лежащие на одной прямой;
б) хорда, проходящая через центр окружности;
в) прямая, проходящая через две точки и центр окружности.
3) Закончить определение: центр окружности – это...
а) точка, куда ставится ножка циркуля при начертании окружности;
б) середина окружности;
в) точка, равноудаленная от всех точек окружности.
4) Закончить определение: дуга окружности – это...
а) часть окружности, выделенная точками;
б) часть окружности, ограниченная двумя точками;
в) часть окружности, ограниченная хордой.
5) Определить, на сколько дуг делят окружность две точки, лежащие на окружности:
а) на одну; б) на две.
6) Как изображается хорда на чертеже окружности? Выбрать правильный ответ:
а) прямой линией;
б) дугой окружности;
в) отрезком с концами, лежащими на окружности.
7) Как называется отрезок, соединяющий центр окружности с любой точкой окружности? Выбрать правильный ответ:
а) длина окружности;
б) радиус окружности;
в) половина диаметра окружности.
8) Найти на рисунке:
а) хорду (рис. 1);
б) диаметр (рис. 2).
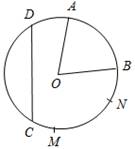
Рис. 1 Рис. 2
Урок22. Задачи на построение
|
Цель деятельности учителя |
Создать условия для формирования представления о новом классе задач – на построение геометрических фигур с помощью циркуля и линейки без масштабных делений, для рассмотрения основных (простейших) задач этого типа |
||
|
Термины и понятия |
Окружность, центр, радиус, диаметр, хорда, дуга окружности, перпендикуляр, биссектриса, отрезок, угол |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют решать простейшие задачи на построение |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||
|
Образовательные |
• Задания для фронтальной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить правильность выполнения домашнего задания |
(Ф/И) 1. Сообщить результаты самостоятельной работы и проанализировать основные ошибки. 2. Проверить решение дополнительной задачи.
1) ∆ОKА= ∆ОKС по двум сторонам и углу между ними (ОА = ОС, как радиусы одной окружности; ОK – общая сторона; ÐAOK = ÐСОK, так как ОЕ – биссектриса угла АОС). Отсюда KА = KС. 2) По условию задачи РKСО = 3R, где R – радиус окружности. ОK = R, ОС = R, следовательно, KС = R. 3) По условию задачи KЕ = KО, а так как KО = R, то KЕ = R. По доказанному KС = R,но KС = АK, следовательно, АK = R. Итак, получили, что KО = R, KE = R, KA = R, KC = R, то есть точки Е, А, С и О равноудалены от точки K и лежат на одной окружности |
||
|
II этап. Беседа |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ознакомить с этапами задачи на построение |
(Ф/И) – Мы уже имели дело с геометрическими построениями: проводили прямые, откладывали отрезки, равные данным, чертили углы, треугольники и другие фигуры с помощью различных инструментов. При построении отрезка заданной длины использовалась линейка с миллиметровыми делениями, а при построении угла заданной градусной меры – транспортир. Но, оказывается, многие построения в геометрии могут быть выполнены с помощью только циркуля и линейки без делений. В дальнейшем, говоря о задачах на построение, мы будем иметь в виду именно такие построения. Задачи на построение с помощью циркуля и линейки являются традиционным материалом, изучаемым в курсе планиметрии. Обычно эти задачи решаются по схеме, состоящей из четырех частей (см. с. 95–96 учебника). Сначала рисуют (чертят) искомую фигуру и устанавливают связи между данными задачи и искомыми элементами. Эта часть решения называется анализом. Она дает возможность составить план решения задачи. Затем по намеченному плану выполняется построение с помощью циркуля и линейки. После этого нужно доказать, что построенная фигура удовлетворяет условиям задачи. И наконец, необходимо исследовать, при любых ли данных задача имеет решение и если имеет, то сколько решений. В тех случаях когда задача достаточно простая, отдельные части, например анализ или исследование, можно опустить. В 7 классе мы будем решать простейшие задачи на построение с помощью циркуля и линейки |
||
|
III этап. Задачи на построение |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Отработать навыки |
(Г) Разделить весь класс на шесть групп,
каждая из которых готовит решение одной из задач на построение 1) На данном луче от его начала отложить отрезок, равный данному (§ 22). 2) Отложить от данного луча угол, равный данному (§ 23). 3) Построить биссектрису данного угла (§ 23). 4) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка (§ 23). 5) Построить середину данного отрезка (§ 23). 6) Через точку, не лежащую на прямой, построить прямую, перпендикулярную данной (задача № 153) |
||
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Из каких этапов состоит решение любой задачи на построение? – Перечислите задачи на построение. – Оцените свою работу на уроке |
(И) Домашнее задание: ответить на вопросы 17–21 на с. 49; решить задачи № 149, 154; повторить материал пунктов 11–21. Найти примеры задач на построение, которые нельзя решить только с помощью циркуля и линейки |
||
Урок23. Задачи на построение
|
Цель деятельности учителя |
Создать условия для закрепления у учащихся навыков решения простейших задач на построение, для обучения решению задач на построение |
|||
|
Термины и понятия |
Окружность, центр, радиус, диаметр, хорда, дуга окружности, перпендикуляр, биссектриса, отрезок, угол |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют решать простейшие задачи на построение |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Задания для индивидуальной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Задания для индивидуальной работы |
|||
|
Проверить уровень сформированности теоретических знаний по теме |
(И) Проверка усвоения теоретического материала (можно осуществить по вариантам). 1-й вариант: на данном луче от его начала отложить отрезок, равный данному. 2-й вариант: отложить от данного луча угол, равный данному. 3-й вариант: построить биссектрису данного угла. 4-й вариант: построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка. 5-й вариант: построить середину данного отрезка. 6-й вариант: через точку, не лежащую на прямой, построить прямую, перпендикулярную данной |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Отработать практичес-кие навыки решения задач на построение |
(Ф/И) Организует деятельность 1. Решить задачу № 150. 2. Решить задачи № 148, 151, 155 |
№ 150. Построить:МÎОкр. (О; r), такую, чтобы АМ = PQ.
Возможны 3 случая: 1) 2) 3)
AM = PQ, AM¢ = PQ. MA = PQ. Нет решения. (2 точки) (1 точка) № 148.
№ 151. Построение: 1) С помощью циркуля построим ÐYXQ, равныйÐВАС. 2) От луча XQ с помощью циркуля отложим ÐQXZ, равный ÐВАС. 3) Получим ÐYXZ = 2ÐВАС, что и требовалось построить.
Построение: 1) С помощью треугольника построим ÐАОВ = 90°. 2) Построим биссектрису ОЕ, получили ÐАОЕ = ÐВОЕ = 45°. 3) Построим OF – биссектрису ÐАОЕ, получим ÐАOF = ÐЕОF = 22°30¢
|
||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Зачем необходимо уметь решать задачи на построение? |
(И) Домашнее задание: написать эссе на
тему «Для чего мне нужно уметь |
|||
Урок24. Решение задач
|
Цель деятельности |
Создать условия для закрепления навыков решения задач на применение признаков равенства треугольников, на построение с помощью циркуля и линейки |
|||
|
Термины и понятия |
Треугольники, окружность, дуга окружности |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: умеют выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: умеют самостоятельно ставить цели, понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для письменной работы. • Чертежи к задачам |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить выполнение домашнего задания |
(Ф/И) 1. Проверка домашнего задания. 2.Понятие трисекции угла. – Трисекция
угла – задача о делении заданного угла на три равные
части построением с помощью циркуля 3. Письменная работа на проверку навыков решения задач на построение с помощью циркуля и линейки. Вариант I 1) Отложить от данного луча угол, равный данному. 2) Построить середину данного отрезка. Вариант II 1) Построить биссектрису данного неразвернутого угла. 2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать |
(Ф/И) Организует деятельность уча- 1. Решение задач по готовым чертежам.
Рис. 1
Рис. 2
Рис. 3 1) Рис. 1. а) Дано: АВ = АС, ÐACE = ÐABD. Доказать: ∆АСЕ = ∆ABD. б) Дано:АЕ = 15 см, ЕС =
10 см, Найти: стороны ∆ABD. 2) Рис. 2. Дано: АО = ОС, ÐВАО = ÐDCO. Доказать: АВ = CD. 3) Рис. 3. Дано:АВ = DC, AD
= ВС, РАВС = 15 см, Найти: АС. 2. Решение задач № 152 и 165 на доске |
№ 152. Построение: 1) Построим окружность с центром О и произвольным радиусом. Окружность пересечет стороны угла в точках М и N. 2) Построим 2 окружности с одинаковым радиусом больше половины длины отрезка МN. Одна окружность с центром М, а другая с центром N. Эти окружности пересекутся в точке K. 3) Соединим лучом О и K – это и есть искомый луч, который разделил ÐАОВ на ÐАОХ и ÐВОХ.
Рис. 4 № 165. Дано: АВÇCD = О. АО = ОВ, СО = ОD, KÎAC, K1ÎBD, AK = BK1. Доказать: a) OK = OK1; б) ОÎKK1.
Рис. 5 Доказательство: 1) Рассмотрим DАОС и DВОD. АО = ОВ (по усл.), СО = ОD (по
усл.), ÐАОС = ÐВОD (вертикальные), DАОС = DВОD (по двум сторонам 2) Рассмотрим DAKO и DBK1O. AK = BK1(по усл.), ÐА = ÐВ (из п. 1), DAKO и BK1O
(по двум сторонам и углу между ними), тогда ÐAOK = 3) АВ – отрезок по условию. ÐAOK = ÐBOK1 (из п. 2), тогда ÐAOK |
||
|
III этап. Самостоятельная работа |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Проверить уровень сформированности теоретических знаний |
(И) Работа выполняется на листках и сдается на проверку учителю. Вариант I 1. На рисунке АВ = АС и ÐACE = ÐABD.
Рис. 6 1) Докажите, что DACE = DABD. 2) Найдите стороны треугольника ABD, если АЕ = 15 см, ЕС = 10 см, АС = 7 см. 2. Известно, что в треугольниках АВС и А1В1С1ÐА = ÐА1, АВ = А1В1, АС = А1С1. На сторонах ВС и В1С1 отмечены точки K и K1, такие, что CK = C1K1. Докажите, что DABK = DA1B1K1. Вариант II 1. На рисунке АО = СО и ÐВАО = ÐDСО.
Рис. 7 1) Докажите, что DAОВ = DDСО. 2) Найдите углы DAОВ, если ÐОСD = 37°, ÐОDС = 63°, ÐСОD = 80°. 2. Известно, что в треугольниках АВС и А1В1С1ÐВ = ÐВ1, АВ = А1В1 и ВС = В1С1. На сторонах АС и А1С1 отмечены точки D и D1, так что АD = А1D1. Докажите, что DВDС = DВ1D1С1 |
|||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Что повторили на уроке? – Оцените свою работу на уроке |
(И) Домашнее задание: повторить материал п. 15–20; решить № 158, 166 |
|||
Урок25. Решение задач
|
Цель деятельности учителя |
Создать условия для закрепления навыков решения задач на применение признаков равенства треугольников, проверки знаний учащихся, подготовки учащихся к предстоящей контрольной работе |
||
|
Термины и понятия |
Треугольники, окружность |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют применять изученные понятия, результаты, методы для решения задач практического характера |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||
|
Образовательные |
• Карточки для устного опроса. • Задачи для фронтальной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить уровень сформированности теоретических знаний |
(И) 1.Анализ и сообщение результатов самостоятельной работы. 2. Устный опрос учащихся у доски по карточкам (см. Ресурсный материал) |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу. В равнобедренном треугольнике МDK длина основания МK относится к длине боковой стороны МD как 3 : 4. Найдите стороны этого треугольника, если периметр его равен 33 см. 2. Решить задачу самостоятельно. В равнобедренном треугольнике длина боковой стороны относится к длине основания как 2 : 3. Найдите стороны треугольника, если периметр его равен 28 см. (Г) 3. Решить № 175 с вынесением решения на доску и обсуждением. Описание способа построения биссектрисы угла с опорой на данную задачу. 1) Построить
окружность с центром 2) Построить
окружности с центрами 3) Построим отрезки АD = ВС. 4) Отрезки пересекутся в точке Е. 5) Соединим лучом вершину угла с точкой Е. Получим луч ОЕ – искомая биссектриса |
1. Решение: Пусть на одну часть приходится х см,
тогда МK = 3х см, По условию Р = 33 см, значит, 3х + 4х + 4х = 33; 11х = 33; х = 3. МK = 9 см, МD = DK = 12 см. Ответ: 9 см; 12 см; 12 см.
№ 175. Дано: ОА = ОВ, АС = BD. Доказать: ОЕ – биссектриса.
Доказательство: 1) Рассмотрим DAOD и DBCO. ÐО – общий, ОА =
ОВ (по усл.), êêêê ОС = ОА + АС). DADO = DВСО (по двум сторонам и
углу между ними), тогда 2) ÐOAD и Ð1 – смежные, значит, Ð1 = 180° – ÐOAD. ÐОВС 3) Рассмотрим DBЕD и DАЕС. Ð1 = Ð2 (из п. 2), ÐD = ÐС 4) Рассмотрим DOЕD и DОСЕ. ОЕ – общая, ОD = ОС (из п. 1), |
|
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Оцените свою работу на уроке. – Оцените свою работу в группе |
(И) Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 15–23; решить задачи № 170, 171 |
||
Ресурсный материал
Карточки для устного опроса
Вариант I
1. Сформулируйте первый признак равенства треугольников.
2. На рисунке 1 АВ = DВ, Ð1 = Ð2. Докажите, что ∆АВС = ∆DВС.
3. В треугольниках АВС и А1В1С1АВ = А1В1, АС = А1С1, ÐА = ÐА1. На сторонах АС и А1С1 отмечены точки D и D1 так, что СD = С1D1. Докажите, что ∆АВD = ∆А1В1D1.
Вариант II
1. Сформулируйте второй признак равенства треугольников.
2. На рисунке 2 Ð1 = Ð2, Ð3 = Ð4. Докажите, что ∆АВD = ∆СВD.
3. В треугольниках АВС и А1В1С1 проведены биссектрисы АD и А1D1. Докажите, что ∆АВС = ∆А1В1С1, если DС = = D1С1, ÐС = ÐС1, ÐАDС = ÐА1D1С1.
Вариант III
1. Сформулируйте третий признак равенства треугольников.
2. На рисунке 3 АВ = DС, ВС = АD. Докажите, что ∆АВС = ∆СDА.
3. На рисунке 4 АВ = DС, ВK = DМ, АМ = СK. Докажите, что ∆АDМ = ∆СВK.
Вариант IV
1. Сформулируйте свойство углов равнобедренного треугольника.
2. На рисунке 5 АВ = ВС, АD = DС. Докажите, что ∆ВАD = ∆ВСD.
3. В равнобедренном треугольнике АВС на основании АС взяты точки D и Е так, что АD = СЕ. Докажите, что треугольник DВЕ равнобедренный.
Вариант V
1. Сформулируйте свойство биссектрисы, проведенной к основанию равнобедренного треугольника.
2. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса ВD, ÐАВD = 37°, АС = 25 см. Найдите ÐВ,ÐВDС и DС.
3. В равнобедренном треугольнике СDЕ с основанием DЕ проведена биссектриса СF. Найдите СF, если периметр треугольника СDЕ равен 84 см, а периметр треугольника СFE равен 56 см.
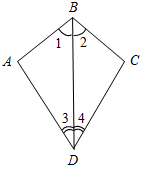
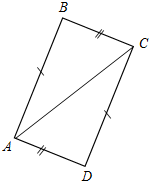
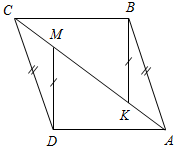
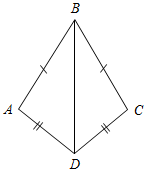
Рис. 1 Рис. 2 Рис. 3 Рис. 4 Рис. 5
\
Урок26. Решение задач. Подготовка к контрольной работе
|
Цель деятельности учителя |
Создать условия для закрепления навыков решения задач на применение признаков равенства треугольников, для проверки знаний учащихся, подготовки к предстоящей контрольной работе |
||
|
Термины и понятия |
Треугольники, окружность |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные |
• Чертежи к заданиям |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Повторить признаки равенства треугольников |
(Ф/И) 1. Обсудить вопросы учащихся по домашнему заданию. 2. Выполнить задание. Равносторонний треугольник изображен на рисунке…
а)б)в)г) 3. Выполнить задание.
Треугольники, изображенные на рисунке… а) равны по двум сторонам и углу между ними; б) равны по стороне и двум прилежащим к ней углам; в) равны по трем сторонам; г) не равны |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся: решение задач № 177, 178, 179 на доске и в тетрадях |
№ 177. Дано:DAВC, DA1В1C1, АВ = А1В1, АС = А1С1, ÐА = ÐА1, KÎАС, LÎВС, K1ÎА1С1, L1ÎВ1С1, АK = А1K1, LС = L1С1.
Рис. 1 Доказательство: 1) Рассмотрим DAВC и DA1В1C1. АВ = А1В1 (по
усл.), АС = А1С1 (по усл.), 2) Рассмотрим DLСK и DL1С1K1, LС = L1С1 (по усл.), ÐС = ÐС1 (из п. 1), KC = C1K1 (так как KC = АС – АK êêêê K1C1 = А1С1 – А1K1). DLСK = DL1С1K1 (по двум сторонам и углу между ними), тогда LK = L1K1 (по определению равных треугольников). 3) Рассмотрим DABL и DA1B1L1, АВ = А1В1 (по усл.), ÐВ = ÐВ1 (из п. 1), BL = B1L1 (так как BL = ВС – LС êêêê B1L1 = B1С1 – L1C1). DABL = DA1B1L1 (по двум сторонам и углу между ними), тогда AL = A1L1 (по определению равных треугольников), что и требовалось доказать. № 178.
Доказать: по крайней мере, два из трех отрезков AD, BD и CD не равны друг другу.
Рис. 2 Доказательство: 1) Предположим, что AD = BD = CD. 2) Следовательно, DAВD, DBDC и DADC – равнобедренные,
значит, Ð1 = Ð2, 3) Это противоречит теореме о том, что через точку, не лежащую на прямой, можно провести единственный перпендикуляр к данной прямой, а у нас получилось 3. 4) Вывод: наше предположение неверно,
следовательно, по крайней мере, два № 179. Дано:DAВC, АВ = АС, РÎАВ, QÎАС, ХÎВС, ВХ = ХС, ÐРХВ = ÐQXC. Доказать: BQ = CP.
Рис. 3 Доказательство: 1) Так как DAВC – равнобедренный, ÐВ = ÐС.
3) Рассмотрим DCQВ и DВРС. CQ = РВ (из п. 2), СВ – общая, ÐС = ÐВ (из п. 1), DСОВ = DВРС (по двум сторонам и углу между ними), тогда QB = CP, что и требовалось доказать |
|
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Какие трудности у вас возникали в процессе решения задач? – Составьте синквейн к уроку |
(И) Домашнее задание: решить № 180, 182, 184 |
||
Урок27. Контрольная работа № 2
|
Цель деятельности |
Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала |
|||
|
Термины и понятия |
Признаки равенства треугольников, равнобедренный треугольник, равносторонний треугольник, медианы, биссектрисы, высоты треугольника |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Задания для контрольной работы |
|||
|
I этап. Выполнение контрольной работы |
||||
|
Цель деятельности |
Задания для контрольной работы |
|||
|
Проверить уровень знаний, умений и навыков по изученному материалу |
(И) Учащиеся выполняют задания контрольной работы (см. Ресурсный материал) |
|||
|
II этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Что выполняли на уроке? – Какие задания вызвали затруднения? Почему? – Как оцениваете свою работу на уроке? |
(И) Домашнее задание: повторить материал пунктов 2–21 |
|||
![]() Ресурсный материал
Ресурсный материал
Контрольная работа
Вариант I
1. Дано: АО = ВО, СО = DO, СО = 5 см, ВО = 3 см, BD = 4 см (рис. 1).
Найти: периметр ∆САО.
Рис. 1
2. В равнобедренном треугольнике АВС точки K и М являются серединами боковых сторон АВ и ВС соответственно. BD – медиана треугольника. Докажите, что ∆BKD = ∆BMD.
3. Даны неразвернутый угол и отрезок. На сторонах данного угла постройте точки, удаленные от вершины угла на расстояние, равное половине данного отрезка.
4*. Прямая МK разбивает плоскость на две полуплоскости. Из точек М и K в разные полуплоскости проведены равные отрезки МА и KB, причем ÐАМK = ÐВKМ. Какие из высказываний верные?
![]() а) ∆АМВ = ∆АKВ;
б) ÐAKM = ÐBMK; в) ∆МKА = ∆KМВ; г) ÐAMB = ÐKМВ.
а) ∆АМВ = ∆АKВ;
б) ÐAKM = ÐBMK; в) ∆МKА = ∆KМВ; г) ÐAMB = ÐKМВ.
Вариант II
1. Дано: АВ = CD, BC = AD, AC = 1 см, AD = 6 см, АВ = 4 см (рис. 2).
Найти: периметр ∆ADC.
Рис. 2
2. В равнобедренном треугольнике АВС точки K и М являются серединами боковых сторон АВ и ВС соответственно. BD – медиана треугольника. Докажите, что ∆AKD = ∆CMD.
3. Даны неразвернутый угол и отрезок. На биссектрисе данного угла постройте точку, удаленную от вершины угла на расстояние, равное данному отрезку.
4*. Прямая АВ разбивает плоскость на две полуплоскости. Из точек А и Вв разные полуплоскости проведены равные отрезки AD и ВС, причем ÐBAD = ÐABC. Какие из высказываний верные?
a) ∆CAD = ∆BDA; б) ÐDBA = ÐCAB; в) ÐBAD = ÐBAC; г) ÐADB = ÐBCA.
Урок28. Работа над ошибками
|
Цели деятельности учителя |
Создать условия для устранения пробелов в знаниях учащихся; совершенствовать навыки решения задач по теме «Треугольники» |
||
|
Термины и понятия |
Треугольники, окружность |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют применять изученные понятия, результаты, методы для решения задач практического характера |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
||
|
Образовательные |
• Задания для парной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проанализировать затруднения, возникшие при решении контрольной работы |
(Ф/И) 1. Сообщить учащимся результаты контрольной работы. 2. Решить задачи, вызвавшие наибольшее затруднение |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать |
(П) Учащимся предлагается решить любые три
задачи из представленных. Учитель выступает в роли консуль- Задача 1. В равнобедренном треугольнике ABC с основанием АС проведены медианы АЕ и CD. Докажите, что: а) ∆АВЕ = ∆CBD; б) ∆DOE и ∆АОС – равнобедренные (О – точка пересечения АЕ и CD); в) ОВ – биссектриса ÐDOE. Задача 2. В равнобедренном ∆АВС с основанием АС на сторонах АВ и ВС отмечены соответственно точки М и N так, что ÐACM = ÐCAN. Докажите, что: а) ∆MBN – равнобедренный; б) ВО^MN (О – точка пересечения AN и CM). Задача 3. Треугольники АВС и DEF – равнобедренные и равные. Найти периметр ∆АВС, если DE = 4 см, EF = 5 см. Задача 4. Дано: АВ = АМ, АС = АK, ÐВАK = ÐСАМ.
Перечислите все пары равных треугольников с вершинами в точках А, В, K, С, М. Задача 5.
Докажите, что отрезки, соединяющие вершины равносторонних треугольников (отличные от вершин равнобедренного) с серединой основания равнобедренного треугольника, равны между собой |
||
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – В чем возникли затруднения? Почему? – Оцените свою работу и работу своего напарника |
(И) Домашнее задание: решить оставшиеся задачи |
||
Урок29. Определение параллельных прямых.
Признаки параллельности двух прямых
|
Цель деятельности |
Создать условия для введения понятия параллельных прямых, рассмотрения признака параллельности двух прямых, связанного с накрест лежащими углами |
|||
|
Термины и понятия |
Параллельные прямые, накрест лежащие углы, соответственные углы, односторонние углы |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Тест. • Задания для фронтальной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проанализировать ошибки, допущенные в контрольной работе |
(Ф/И) 1. Указать ошибки, допущенные учащимися при выполнении работы. 2. Решить задачи, вызвавшие затруднения у учащихся |
|||
|
II этап. Учебно-познавательная деятельность |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Ввести понятие параллельных прямых, накрест лежащих углов, соответственных, односторонних углов |
(Ф/И) 1. Тест (см. Ресурсный материал). Учащиеся решают
задания самостоятельно. Важно подчеркнуть, что за данный тест оценки в журнал
– Начертите прямые а и b и прямую с так, чтобы а и b пересекались с прямой с. – Сколько неразвернутых углов изображено на рисунке?
Рис. 1 – Запишите в тетрадях: с – секущая по отношению к прямым а и b. Ð3 и Ð5; Ð4 и Ð6 – накрест лежащие углы. Ð4 и Ð5; Ð3 и Ð6 – односторонние углы. Ð1 и Ð5; Ð2 и Ð6; Ð4 и Ð8; Ð3 и Ð7 – соответственные углы.
Рис. 2 – Назовите накрест лежащие углы при прямых а и b и секущей с. – Назовите односторонние углы при прямых b и с и секущей а. – Назовите соответственные углы при прямых а и с и секущей b.
Рис. 3 Докажите:Ð3 = Ð6; Ð3 = Ð7; Ð6 = Ð2; Ð4 + Ð6 = 180°; Ð5 + Ð2 = 180°. 4. Доказательство признаков параллельности прямых. Признак параллельности прямых, использующий накрест лежащие углы, можно доказать по учебнику |
|||
|
III этап. Закрепление изученного материала |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать навыки решения задач на закрепление изученного материала |
(Ф/И)Организует деятельность учащихся. 1. Решить задачу. Найти пары параллельных прямых
Рис. 4 Рис. 5
Рис. 6 2. Решить задачу № 191 на доске и в тетрадях |
№ 191. Дано:DАВС, ВK – биссектриса, ВМ = KМ.
Рис. 7 Доказательство: 1) Так как ВМ = KМ, то DВМK – равнобедренный, значит, 2) Ð1 = Ð2 (по усл.), Ð2 = Ð3 (из п. 1), Ð1 = Ð3, а так как |
||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – В чем заключается первый признак параллельности прямых? – Составьте синквейн к теме урока |
(И) Домашнее задание: изучить пункты
24–25 (первый признак); решить задачи |
|||
Ресурсный материал
Тест
1. Выбрать рисунки с пересекающимися прямыми.
а) 1а; б) 1б; в) 1в.
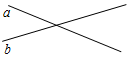
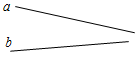
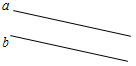
а) б) в)
Рис. 1
2. Завершить высказывание, выбрав нужный пункт.
Пересекающиеся прямые имеют...
а) на чертеже одну общую точку;
б) одну общую точку.
3. Указать номера рисунков, на которых изображены параллельные прямые.
а) 2а; б) 2б; в) 2в.
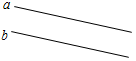
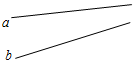
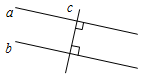
а) б) в)
Рис. 2
4. Указать неправильную концовку определения.
Две прямые на плоскости называются параллельными...
а) если они находятся на постоянном расстоянии друг от друга;
б) если они не пересекаются на плоскости;
в) если они обе перпендикулярны к третьей прямой;
г) если они не пересекаются на чертеже.
5. Указать рисунки, на которых изображены параллельные отрезки.
а) 3а; б) 3б; в) 3в; г) 3г.
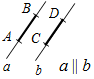
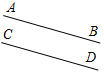
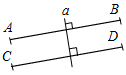
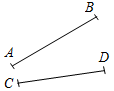
а) б) в) г)
Рис. 3
6. Указать правильную концовку определения.
Два отрезка называются параллельными, если они...
а) оба перпендикулярны третьей прямой;
б) лежат на параллельных прямых;
в) имеют одинаковое расстояние между концами;
г) не пересекаются на плоскости.
7. Указать рисунки, на которых изображены параллельные лучи.
а) 4а; б) 4б; в) 4в; г) 4г.
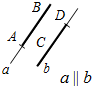
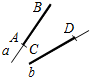
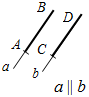
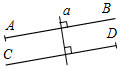
а) б) в) г)
Рис. 4
Ответы: 1 – a, б; 2 – б; 3 – в; 4 – г; 5 – а, в; 6 – б; 7 – а, в, г.
Урок30. Признаки параллельности двух прямых
|
Цель деятельности |
Создать условия для изучения признаков параллельности двух прямых, связанных с односторонними и соответственными углами, и демонстрации их применения при решении задач |
||||
|
Термины и понятия |
Параллельные прямые, накрест лежащие углы, соответственные углы, односторонние углы |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||||
|
Образовательные |
• Задания для фронтальной работы. • Тест |
||||
|
I этап. Активизация знаний учащихся |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Систематизировать |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Повторение доказательства признака параллельности двух прямых, использующего накрест лежащие углы, по готовому чертежу на доске. 3. Устная работа по готовым чертежам на доске. Задание: Найти пары параллельных прямых (отрезков) и доказать их параллельность.
Рис. 1 Рис. 2 Рис. 3 |
||||
|
II этап. Изучение новой темы |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Рассмотреть признаки параллельности
прямых, связанные |
(Ф) 1.По рисунку 102 учебника, заранее
начерченному на доске, учитель вместе с учащимися доказывает теорему 2. Учащиеся самостоятельно изучают признак параллельности прямых, связанный с соответственными углами, и записывают доказательство теоремы в тетрадях. 3. Решить задачи по готовым чертежам на заготовленных плакатах (устно). Задание: Найдите пары параллельных прямых и докажите их параллельность.
Рис. 4 Рис. 5 Рис. 6 |
||||
|
III этап. Тест |
|||||
|
Цель деятельности |
Тестовые задания |
||||
|
Проверить уровень сформированности теоретических знаний |
(И)Выполнить тест с самопроверкой (см. Ресурсный материал) |
||||
|
IV этап. Решение задач по готовым чертежам |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
На простейших задачах отработать признаки параллельности прямых |
(Ф/И) Решение задач (устно). 1) Параллельны ли прямые а и b? Почему?
а) б) в) Рис. 7 2) Доказать: АВ || DE. 3) Доказать:АВ || MN.
Рис. 8 Рис. 9 |
||||
|
V этап. Решение задач |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Совершенствовать навыки решения задач |
(Ф/И) Организует деятельность учащихся. 1. Решить № 192 на доске и в тетрадях. 2. Познакомиться с практическими
способами построения параллельных прямых (п. 26) 3. Выполнить задание |
№ 192. Дано:DАВС, ÐА = 40°, ÐВСЕ, ÐАСВ – смежные, ÐВСЕ = 80°, CK – биссектриса ÐВСЕ. Доказать:АВ || CK.
1) Так как CK – биссектриса ÐВСЕ, то ÐВCK = ÐKCЕ = 40°. 2) ÐВАС и ÐKCЕ – соответственные
при прямых АВ, CK и секущей АС, № 195. а || ВС, b || АВ
Рис. 11 |
|||
|
VI этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) – Перечислите признаки параллельности прямых. – Оцените свою работу на уроке. – Задайте три вопроса по теме урока |
(И) Домашнее задание: изучить пункты 24–26; ответить на вопросы 1–6 на с. 66; решить задачи № 193, 194 |
||||
Ресурсный материал
Тест
![]() 1. Выберите верные утверждения (по рис. 1):
1. Выберите верные утверждения (по рис. 1):
а) Ð1 и Ð3 – вертикальные; д) Ð2 и Ð4 – смежные;
б) Ð5 и Ð1 – односторонние; е) Ð7 и Ð1 – накрест лежащие;
в) Ð7 и Ð6 – соответственные; ж) Ð3 и Ð7 – односторонние.
г) Ð5 и Ð3 – накрест лежащие;
Рис. 1
2. Выберите верные утверждения (по рис.1).
Прямые а и b параллельны, если…
a) Ðl = Ð3; д) Ð5 = Ð3;
б) Ð8 + Ð5 = 180°; e) Ð2 = Ð6;
в) Ð7 = Ð6; ж) Ð1 + Ð4 = 180°;
г) Ð8 + Ð3 = 180°; и) Ð1 + Ð7 = 180°.
3. Укажите продолжения высказывания, не соответствующие действительности.
Прямые не параллельны, если при пересечении двух прямых секущей…
а) сумма односторонних углов не равна 180°;
б) сумма соответственных углов равна 180°;
в) вертикальные углы не равны;
г) накрест лежащие углы не равны;
д) сумма смежных углов не равна 180°;
е) соответственные углы не равны.
Ответы: 1 – а, в, г, д, ж; 2 – б, в, д, е, и; 3 – а, г, е.
Урок 31. Решение задач
на применение признаков параллельности прямых
|
Цели деятельности учителя |
Создать условия для закрепления и систематизации изученного материала, обучения применению признаков параллельности прямых при решении задач; способствовать развитию логического мышления учащихся; содействовать воспитанию аккуратности при построении чертежей на доске и в тетрадях |
|||
|
Термины и понятия |
Параллельные прямые, накрест лежащие углы, соответственные углы, односторонние углы |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют геометрическим языком, умеют его использовать для описания предметов окружающего мира, имеют достаточно высокий уровень пространственных представлений и изобразительных умений, владеют навыками геометрических построений |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать самостоятельно. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Чертежи к задачам. • Задания для самостоятельной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Систематизировать |
(Ф/И) 1. Проверить правильность выполнения домашнего задания. 2. Провести теоретический опрос по признакам параллельности прямых. 3. Решить задачи по готовым чертежам (устно). 1) Докажите, что а || b. 2) Докажите, что а || с. 3)Докажите, что а || b и т || п, если Ð1 = Ð2 = Ð3.
Рис. 1 Рис. 2 Рис. 3 4) Дано:Ð1 = 83°, Ð2 больше Ð1 на 14°. 5) Дано:Ð2 = 114°, Ð1 меньше Ð2 на 20°. Параллельны ли прямые MN и AB? Параллельны ли прямые СЕ и AB?
Рис. 4 Рис. 5
|
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 190 по рисунку 109 (на доске и в тетрадях). 2. Решить задачу № 213 по рисунку 121 (на доске и в тетрадях). 3. Решить задачу № 215 по рисунку 122 (устно). Указание: рисунок 122 заранее
перенести |
Дано:АВ = ВС, АD = DЕ, ÐС = 70°, ÐЕАС = 35°. Доказать:DЕ || АС.
Рис. 6 Доказательство: 1) Так как АВ = ВС, то ÐА = ÐС = 70° (свойство равнобедренного треугольника). 2) Так как ÐЕАС = 35°, ÐА = 70°, то ÐDАЕ = 35°. 3) Так как DАDЕ – равнобедренный, то ÐDАЕ = ÐDЕА = 35° (по свойству). 4) ÐDЕА = ÐЕАС = 35°. ÐDЕА и ÐЕАС – накрест лежащие при прямых DЕ и АС и секущей АЕ. DЕ || АС, что и требовалось доказать.
Дано: СЕ = ЕD, ВЕ = EF, KE || AD. Доказать: KE || BC.
Рис. 7 Доказательство: 1) Рассмотрим DВСF и DFDЕ. ВЕ = EF (по усл.), СЕ = ЕD (по
усл.), Ð1 = Ð2 2) ÐСВЕ = ÐDFЕ – накрест лежащие
при прямых BC и AD и секущей ВF, 3) KE || AD (по усл.), BC || AD (из п. 2), тогда KE || BC (свойство параллельных прямых), что и требовалось доказать |
||
|
III этап. Самостоятельная работа |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Проверить умение применять признаки параллельности при решении задач |
(И) Самостоятельная работа выполнятеся на листках и сдается на проверку учителю (см. Ресурсный материал) |
|||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Оцените свою работу на уроке. – Задайте три вопроса по теме |
(И) Домашнее задание: повторить материал пунктов 24–26; решить задачи № 214, 216 |
|||
Ресурсный материал
Самостоятельная работа
Вариант I
1. Параллельны ли прямые d и е, изображенные на рисунке 1?
2. На рисунке 2 точка О – середина отрезков EL и KF. Докажите, что EF || KL.
Вариант II
1. Параллельны ли прямые m и n, изображенные на рисунке 3?
2. На рисунке 4 точка F – середина отрезков MО и NP. Докажите, что MN || PO.
Вариант III
1. Какие из прямых, изображенных на рисунке 5(m, n и p), являются параллельными? Ответ обоснуйте.
2. В равнобедренных треугольниках СDЕ и FPK, изображенных на рисунке 6, Ð1 = Ð2. Докажите, что СD || PF.
Вариант IV
1. На рисунке 7 МD = NP, Ð1 = Ð2. Докажите, что MN || DP.
2. В равнобедренных треугольниках АВС и DЕF, изображенных на рисунке 8, Ð1 = Ð2. Докажите, что AB || EF.
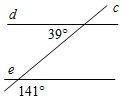
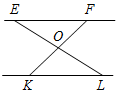
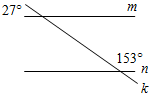
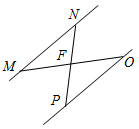
Рис. 1 Рис. 2 Рис. 3 Рис. 4
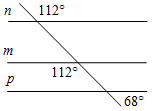
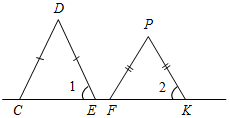

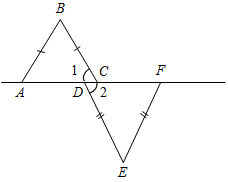
Рис. 5 Рис. 6 Рис. 7 Рис. 8
Урок 32. Об аксиомах геометрии.
Аксиома параллельности прямых
|
Цель деятельности учителя |
Создать условия для формирования представления об аксиомах геометрии, введения аксиомы параллельных прямых и следствия из нее |
||
|
Термины и понятия |
Параллельные прямые, аксиома |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Владеют геометрическим языком, умеют его использовать для описания предметов окружающего мира, имеют пространственные представления и достаточно высокий уровень развития изобразительных умений, навыков геометрических построений |
Познавательные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Регулятивные: умеют выдвигать
гипотезы при решении учебных задач и понимать необходимость Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные |
• Задания для фронтальной работы. • Историческая справка об аксиоме параллельных прямых |
||
|
I этап. Актуализация опорных знаний |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проанализировать ошибки, допущенные в самостоятельной работе |
(Ф/И) 1. Сообщить результаты самостоятельной работы. 2. Проверить правильность выполнения домашнего задания |
||
|
II этап. Беседа по новой теме |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ввести понятие аксиомы, рассмотреть аксиому параллельных прямых |
(Ф/И) 1. Беседа об аксиомах геометрии (см. пункт 27 и приложение 1 учебника). 2. Самостоятельное решение задачи с последующим обсуждением. Задание: Через точку А, не лежащую на прямой а, провести прямую, параллельную прямой а.
1) провести через точку А прямую b так, что a^b; 2) провести через точку А прямую с так, что b^с.
Рис. 1 Доказательство:Ð1 = Ð2 = 90°, то есть накрест лежащие углы при прямых а и с и секущей b равны, следовательно, а || с. Вопросыучащимся: 1) Всегда ли через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной? 2) Сколько прямых, параллельных данной, можно провести через точку, не лежащую на данной прямой? 3) Можно ли доказать, что через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной? – Математики с древних времен пытались доказать данное утверждение. В «Началах» Евклида оно называется пятым постулатом. Попытки доказать пятый постулат Евклида не увенчались успехом, и лишь в XIX веке было окончательно выяснено, что утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой. Огромную роль в решении этого вопроса сыграл русский математик Николай Иванович Лобачевский. Итак, аксиомапараллельных прямыхгласит: «Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной». – Является ли утверждение «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной» аксиомой? Почему? (Это утверждение не является аксиомой, так как оно доказывается.) – Чем отличаются вышеуказанные утверждения? (Аксиома параллельных прямых говорит о единственности такой прямой, а другое утверждение – о существовании такой прямой.) |
||
|
III этап. Закрепление изученного материала |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать навыки решения простейших задач |
(Ф/И) Организует деятельность учащихся. 1. Решить задачи № 196, 197 (устно). Указание: при решении задачи № 197 полезно показать учащимся на рисунке два возможных случая расположения прямых: 1) все четыре прямые пересекают прямую р; 2) одна из четырех прямых параллельна прямой р, а три другие прямые пересекают ее. Эти два случая иллюстрируют ответ на вопрос задачи: по крайней мере, три прямые пересекают прямую р. 2. Разъяснить смысл понятия Записать в тетрадях: «Следствиями называются утверждения, которые выводятся непосредственно из аксиом или теорем». 3. Рассмотреть следствия 1 и 2 4. Решить задачи № 198, 200, 218. 5. Решить задачу № 219 |
№ 218.
Можно ли построить прямую с, такую, что: 1) а || с; 2) сÇb?
Рис. 2 Доказательство: Возьмем любую точку МÏа. По аксиоме параллельных прямых, через точку М можно построить прямую с, параллельную а, и притом только одну. Так как а || с, аÇb, тогда сÇb. Значит, можно построить такую прямую, параллельную прямой а и пересекающую прямую b.
Дано:с Çа, сÇb, с – любая. Доказать: а || b.
Рис. 3 Доказательство: Пусть а || b. Проведем
прямую с || b; с Çа, но сÇb (по построению), |
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Что нового узнали на уроке? – В чем заключается аксиома Евклида? – Составьте синквейн к уроку |
(И) Домашнее задание: изучить пункты 27 и 28; ответить на вопросы 7–11 на с. 66–67 учебника; решить задачи № 217, 199 |
||
Урок33. Свойства параллельных прямых
|
Цель деятельности учителя |
Создать условия для рассмотрения свойств параллельных прямых, демонстрации применения свойств параллельных прямых, закрепления знаний, умений, навыков учащихся по теме «Аксиома параллельных прямых» |
|||||||||||||||
|
Термины и понятия |
Параллельные прямые, аксиома, свойства параллельных прямых |
|||||||||||||||
|
Планируемые результаты |
||||||||||||||||
|
Предметные умения |
Универсальные учебные действия |
|||||||||||||||
|
Владеют геометрическим языком, умеют его использовать для описания предметов окружающего мира, владеют достаточно высоким уровнем развития пространственных представлений и изобразительных умений, навыков геометрических построений |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: считаются с разными мнениями и стремятся к координации различных позиций в сотрудничестве; подбирают аргументы для доказательства своей позиции, формулируют выводы. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|||||||||||||||
|
Организация пространства |
||||||||||||||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||||||||||||||
|
Образовательные |
• Тест. • Таблица |
|||||||||||||||
|
I этап. Актуализация опорных знаний учащихся |
||||||||||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||||||||||
|
Систематизировать теоретический материал |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Тест с последующей самопроверкой (см. Ресурсный материал). (Задания 1 и 2 выполняются одновременно; 3 ученика работают у доски, остальные в тетрадях.) |
|||||||||||||||
|
II этап. Учебно-познавательная деятельность |
||||||||||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||||||||||
|
Ввести свойства параллельных прямых |
(Ф/И) 1. Решение задач. 1) Доказать:АВ || CD. 2) Дано: АВ || CD. Найти:ÐEKC.
Рис. 1 Рис. 2 Следует обратить внимание учащихся, что в первой задаче а || bпо первому признаку параллельности прямых, а вторая задача является обратной первой, и в этом случае мы не знаем, равны ли накрест лежащие углы, если прямые параллельны. Таким образом, перед учащимися поставлена проблема, которую необходимо разрешить. Условие. Пусть а || b, с – их секущая, Ð1 и Ð 2 – накрест лежащие углы, образованные данными прямыми. Требуется выяснить, равны ли Ð1 и Ð 2. Решение этой задачи можно построить так же, как доказательство свойства накрест лежащих углов при параллельных прямых и их секущей по учебнику. Вывод. Если две параллельные прямые пересечены третьей, то накрест лежащие углы равны. – Это утверждение называют свойством накрест лежащих углов при параллельных прямых и их секущей. 2. Информация для учащихся. – Во всякой теореме различают две части: условие и заключение. Условие теоремы – это то, что дано, а заключение – то, что требуется доказать. Вывод. Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы. 3. Беседа о методе доказательства от противного по учебнику. 4. Доказательства
следствия свойства накрест лежащих углов при параллельных прямых и их секущей
Можно предложить учащимся провести доказательства самостоятельно в ходе выполнения упражнений. – Докажите, что если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и другой. – Сформулируйте теорему, обратную признаку параллельности прямых, использующему соответственные углы. Дайте название полученной теореме и докажите ее. – Сформулируйте теорему, обратную признаку параллельности прямых, использующему односторонние углы. Дайте название полученной теореме и докажите ее. – Заполните таблицу.
– В чем заключается разница между этими теоремами? |
|||||||||||||||
|
III этап. Решение задач |
||||||||||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||||||||||
|
На простейших задачах отработать умение применять свойства параллельных прямых |
(Ф/И) Устно решить № 201, 205 по рисунку 117 и № 209 по рисунку 118 |
|||||||||||||||
|
IV этап. Итоги урока. Рефлексия |
||||||||||||||||
|
Деятельность учителя |
Деятельность учащихся |
|||||||||||||||
|
(Ф/И) – Перечислите свойства параллельных прямых. – Что такое доказательство методом от противного? – Оцените свою деятельность на уроке |
(И) Домашнее задание: изучить п. 29;
повторить пункты 15–28; ответить |
|||||||||||||||
Ресурсный материал
Тест
1. Вычеркнуть лишние слова в скобках.
Аксиома – это (очевидное, принятое, исходное) положение геометрии, не требующее (объяснений, доказательств, обоснований).
2. Выбрать окончание формулировки аксиомы параллельных прямых.
Через точку, не лежащую на данной прямой…
а) проходит только одна прямая, параллельная данной;
б) всегда проходит прямая, параллельная данной;
в) проходит только одна прямая, не пересекающаяся с данной.
3. Что может быть следствием аксиомы или теоремы? Указать неверные ответы.
а) Утверждение, не требующее доказательства.
б) Новая теорема, для доказательства которой использована аксиома или теорема.
в) Утверждение, непосредственно выводимое из аксиомы или теоремы.
4. Указать следствия аксиомы параллельных прямых.
а) Если отрезок или луч пересекает одну из параллельных прямых, то он пересекает и другую.
б) Если две прямые параллельны третьей прямой, то они параллельны друг другу.
в) Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
г) Если три прямые параллельны, то любые две из них параллельны друг другу.
д) Если две прямые не параллельны третьей прямой, то они не параллельны между собой.
е) Если прямая пересекает одну из параллельных прямых, то она не может не пересекать другую.
ж) Если две прямые параллельны третьей прямой, то они не могут быть не параллельны между собой.
5. Указать правильный ответ на вопрос.
Если через точку, лежащую вне прямой, проведено несколько прямых, то сколько из них пересекаются с исходной прямой?
а) Неизвестно, так как не сказано, сколько прямых проведено через точку.
б) Все, кроме параллельной прямой.
в) Все, которые имеют на рисунке точку пересечения с исходной прямой.
6. Почему если одна из прямых, проходящих через точку, лежащую вне заданной прямой, параллельна этой прямой, то другие прямые, проходящие через эту точку, не могут быть ей параллельны? Указать неправильный ответ на этот вопрос.
а) Это противоречит аксиоме параллельных прямых.
б) Любая другая прямая, если она также параллельна заданной, совпадет с первой.
в) Все другие прямые имеют точку пересечения с заданной прямой, хотя она может находиться на сколь угодно большом расстоянии от исходной точки.
Ответы: 1. Следует вычеркнуть слова: «очевидно», «принятые», «объяснений», «обоснований»; 2 – а; 3 – а, б; 4 – б, в, е, ж; 5 – б; 6 – в.
Урок34. Свойства параллельных прямых.
Решение задач
|
Цели деятельности учителя |
Создать условия для закрепления знания свойств параллельных прямых в ходе выполнения упражнений и решения задач, для систематизации знаний учащихся; способствовать развитию логического мышления учащихся |
||
|
Термины и понятия |
Параллельные прямые, аксиома, свойства параллельных прямых |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: считаются с разными мнениями и стремятся к координации различных позиций в сотрудничестве; подбирают аргументы для доказательства своей позиции, формулируют выводы. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); парная (П) |
||
|
Образовательные |
• Задания для индивидуальной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Выявить уровень сформированности теоретических знаний |
(Ф/И) 1. Проверка домашнего задания. (И) 2. Проверочная работа на 10 минут. Работа выполняется на листочках и сдается на проверку учителю. Вариант I 1. Сформулируйте аксиому параллельных прямых. 2. Какая теорема называется обратной данной теореме? Приведите примеры теорем, обратных данным. 3. Докажите, что при пересечении двух параллельных прямых секущей соответственные углы равны. ВариантII 1. Объясните, какие утверждения называются аксиомами. Приведите примеры аксиом. 2. Дайте определение параллельных прямых. Какие два отрезка называются параллельными? 3. Докажите, что при пересечении двух параллельных прямых секущей сумма односторонних углов равна 180° |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 203 (П) 2. Решить № 205. (Ф/И) 3. Решить № 220 по готовому чертежу (устно) |
Дано:а || b, с – секущая. а) Ð1 = 150°; б) Ð1 >Ð4 на 70°. Найти: величину углов.
Рис. 1 Решение: а) 1) Если Ð1 = 150° (по усл.), то Ð3 = Ð1 = 150° (как вертикальные); Ð5 = Ð1 = 150° (как накрест лежащие при а || b и секущей с); Ð7 = Ð5 = 150° (как вертикальные). 2) Ð1, Ð4 – смежные, значит, Ð1 + Ð4 = 180° (по свойству), Ð4 = 180° – 150° = 30°; Ð2 = Ð4 = 30° (как вертикальные), Ð8 = Ð4 = 30° (как накрест лежащие при а || b и секущей с); Ð6 = Ð8 = 30° (как вертикальные). Ответ: 30°, 150°, 30°, 150°, 30°, 150°, 30°. б) Если Ð1 >Ð4 на 70°, то примем Ð1 = х, следовательно, Ð4 = х – 70°; так как Ð1, Ð4 – смежные, то х + (х – 70) = 180 2х = 250 х = 125 Ð1 = 125°, Ð4 = 55° Рассуждая аналогично пункту (а), имеем: Ð1 = Ð3 = Ð5 = Ð7 = 125°, Ð2 = Ð4 = Ð6 = Ð8 = 55°.
№ 205. Найти:Ð1.
Рис. 2 Доказательство: 1) Ð2 – вертикальный с углом 73°, значит Ð2 = 73°. 2) Ð2, Ð3 – односторонние при прямых а, b и секущей с. Ð2 + Ð3 = 73° + 107° = 180°, тогда, а || b (по признаку). 3) Ð1, Ð4 – соответственные углы при прямых а || b и секущей d, значит, Ð1 = Ð4 = 92° (по свойству параллельных прямых). Ответ: 92° |
|
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Перечислите свойства параллельных прямых. – Перечислите признаки параллельных прямых. – Оцените свою работу на уроке и работу своего товарища |
(И)Домашнее задание: повторить изученный
материал пунктов 24–29; ответить на вопросы 1–15 на с. 66–67 учебника;
подготовиться к устному опросу; решить |
||
Урок35. Решение задач
|
Цель деятельности учителя |
Создать условия для приведения в систему знаний учащихся по данной теме, четкого понимания учащимися того, когда в задаче нужно применить признак параллельности двух прямых, а когда – свойство параллельных прямых |
|
|
Термины и понятия |
Параллельные прямые, аксиома, свойства параллельных прямых |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Карточки для устного опроса. • Чертежи к задачам |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать теоретические знания учащихся |
(Ф/И) 1. Обсуждение результатов проверочной работы и анализ допущенных ошибок. 2. Проверка правильности выполнения домашней работы. Для этого к доске вызываются трое учащихся и демонстрируют решения домашних задач. 3. Устный опрос учащихся по карточкам (см. Ресурсный материал) |
|
|
II этап. Решение задач по готовым чертежам |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
(И) 1. Решить задачи по готовым чертежам, сделав в тетрадях краткие записи (см. Ресурсный материал) (самостоятельно). (Ф/И) 2. Решить задачу (один ученик решает у доски, остальные в тетрадях). Дано:АВ || DE(рис. 1а). Доказать:Ð1 + Ð2 = Ð3.
а) Рис. 1 б) Подсказка: через точку С проведите прямую, параллельную АВ. Доказательство(см. рис. 1б): 1) Через точку С, не лежащую на прямой АВ, можно провести прямую, параллельную АВ, и притом только одну. 2) Так как KС || АВ, а АВ || DE по условию задачи, то KС || DE. 3) Ð1 = ÐACK, как накрест лежащие при параллельных прямых АВ и KС и секущей АС. 4) Ð2 = ÐKСD, как накрест лежащие при параллельных прямых KС и DE и секущей DС. Так как Ð1 = ÐАСK, Ð2 = ÐKСD, a Ð3 = ÐАСK + ÐKСD, то Ð3 = Ð1 + Ð2, что и требовалось доказать |
|
|
III этап. Самостоятельное решение задач |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Совершенствовать |
(И) Учащимся предложены задачи двух
уровней сложности (см. Ресурсный материал). Они сами выбирают, |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Что повторили на уроке? – Оцените свою работу на уроке |
(И)Домашнее задание: решить № 207 |
|
Ресурсный материал
Карточки для устного опроса
Вариант I
1. Сформулируйте один из признаков параллельности двух прямых.
2. Докажите, что прямые а и b, изображенные на рисунке 1, параллельны, если Ð1 = 36°; Ð8 = 144°.
3. На рисунке 2 прямые АD и ВK параллельны, луч ВD – биссектриса угла АВK, ÐАВK = 80°.
Найдите углы треугольника АВD.
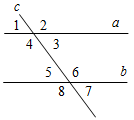
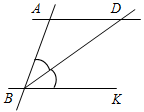
Рис. 1 Рис. 2
Вариант II
1. Сформулируйте аксиому параллельных прямых.
2. Дан треугольник СDЕ. Сколько прямых, параллельных стороне СЕ, можно провести через вершину D?
3. На рисунке 3 отрезки АВ и СD пересекаются в их общей середине М. Через точку В проведена прямая а, параллельная прямой АD. Докажите, что прямая а проходит через точку С.
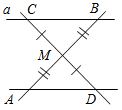
Рис. 3
Вариант III
1. Сформулируйте одно из свойств параллельных прямых.
2. На рисунке 4 прямые а и b параллельны; Ð2 = 132°. Найдите Ð7.
3. На рисунке 5 АВ = ВС; ВF || АС. Докажите, что луч ВF – биссектриса угла СВD.
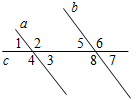
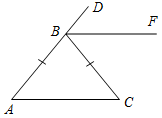
Рис. 4 Рис. 5
Задачи на готовых чертежах для самостоятельного решения
Вариант I
1) Дано: a || b, Ð1 больше Ð2 в 2 раза. 2) Дано: а || b, Ð1 + Ð2 = 122°.
Найти:Ð1, Ð2. Найти:Ð3, Ð4, Ð5, Ð6, Ð7, Ð8.
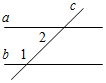
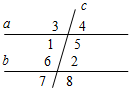
Рис. 1 Рис. 2
3) Дано: AD || BC, Ð1 = 50°, Ð2 = 65°.
Найти:ÐАВС.
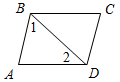
Рис. 3
Вариант II
1) Дано: m || n, Ð2 больше Ð1 на 30°. 2) Дано: a || b, Ð2 + Ð 5 = 240°.
Найти:Ðl, Ð2. Найти:Ðl, Ð3, Ð4, Ð6, Ð7, Ð8.
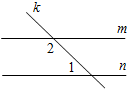
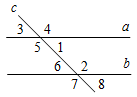
Рис. 4 Рис. 5
3) Дано: CD || EF, Ð1 = 40°, Ð2 = 75°.
Найти:ÐDEF.
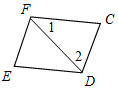
Рис. 6
Ответы для самопроверки:
Вариант I: 1) Ð2 = 60°, Ðl = 120°; 2) Ð4 = Ð7 = 61°, Ð3 = Ð5 = Ð6 = Ð8 = 119°; 3) ÐАВС = 115°.
Вариант II: 1) Ð1 = 75°, Ð2 = 105°; 2) Ð4 = Ð7 = 120°, Ðl = Ð3 = Ð6 = Ð8 = 60°; 3) ÐDEF = 115°.
Самостоятельная работа
I уровень
1) Дано:Ð1 = 60°, Ð2 = 20°, а || b.
Найти:Ð3.
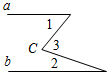
Рис. 1
Решение: через точку С провести прямую, параллельную прямой а, и доказать, что Ð3 = Ð1 + Ð2, Ð3 = 80°.
2) Дано:ÐАОР = 80°, ÐОРS = 80°, ÐESP = 40°. 3) Найти: х, у.
Найти:ÐOFK, ÐKFB.
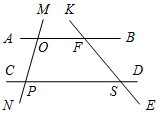
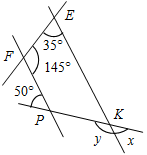
Рис. 2 Рис. 3
Решение:ÐAOP = ÐOPS, тогда АВ || СD, тогда ÐOFK = 40°, ÐKEB = 140°.
4) Дано: АЕ – биссектриса ÐBAD.
Найти:ÐABE, ÐВЕА.
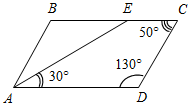
Рис. 4
II уровень
1) Найти: х, у.
Указание: докажите, что РЕ || KF из равенства углов, градусные меры которых 70°, тогда у = 52°, х = 128°.
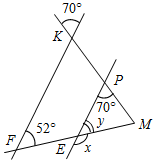
Рис. 5
2) Найти: х, если ÐАВЕ = ÐСВЕ.
Решение:
ÐC + ÐD = 180°, значит, ВС || АD, тогда ÐАЕВ = ÐЕВС = 52°. ÐАВЕ = ÐСВЕ, поэтому ÐАВС = 104°.
Так как ВС || AD, a ÐABC = 104°, то ÐВАЕ = 76°, то есть х = 76°.
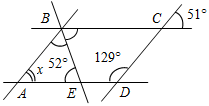
Рис. 6
3) Дано: РТ – биссектриса ÐkРМ.
Найти: х.
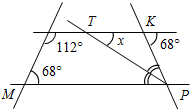
Рис. 7
4) Дано: а || b.
Доказать: ÐМОЕ = 90°.
Указание: Через точку О провести прямую, параллельную прямой МА, и доказать ÐMOE = ÐAMO + ÐOEB.
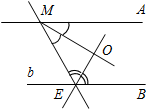
Рис. 8
Урок36. Решение задач
|
Цель деятельности учителя |
Создать условия для приведения в систему знаний учащихся по данной теме; для четкого понимания учащимися того, когда в задаче нужно применить признак параллельности двух прямых, а когда – свойство параллельных прямых; для подготовки к контрольной работе |
||
|
Термины и понятия |
Параллельные прямые, аксиома, свойства параллельных прямых |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию |
Познавательные: осуществляют логические действия. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки, осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные |
• Задания для фронтальной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Систематизировать |
(Ф/И) 1. Сообщить результаты проверочной работы и проанализировать основные ошибки. 2. Ответить на вопросы по домашнему заданию |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать |
(Ф/И) 1. Найти пары параллельных прямых и доказать их параллельность (устно). 1) 2) 3)
2. Решить задачи, сделав краткие записи в тетрадях. 1) Дано: a || b, c – секущая, Ð1 – Ð2 = 32°. 2) Дано: т || п, р – секущая, Ð1 : Ð2 = 3 : 2. Найти:Ð1, Ð2. Найти:Ð1, Ð2.
3) Дано: k || d, l
– секущая, Ð1 = 2,6Ð2. 4)
Дано: a || b, c – секущая, Ð2 = Найти:Ð1, Ð2. Найти:Ð1, Ð2.
5) Дано: т || п, k – секущая, Ð1 = 60 % от Ð2. 6) Дано: KP || NM, ÐNKP = 120°. Найти:Ð1, Ð2. Найти:ÐN, ÐМ.
7) Дано: АС || BK. 8) Дано: KN || MЕ. 9) Дано: AD || BE. Найти:ÐА, ÐАВС. Найти: ÐЕMN. Найти: ÐDCB.
10) Дано: CE || BA, Ð3 = 130°. 11) Дано: TF || RP. Найти:ÐАCD. Найти: ÐRPF,ÐSFT.
12) Найти: ÐKFE. 13) Дано:Ð1 = Ð2 = 30°, AB || DE. Найти:ÐАEB.
|
||
|
III этап. Итоги урока |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Оцените свою работу на уроке. – Составьте синквейн к уроку |
(И)Домашнее задание: повторить материал пунктов 24–29; подготовиться к контрольной работе, просмотрев решение задач по тетрадям; решить задачи, которые не успели выполнить в классе |
||
Урок37. Решение задач
|
Цель деятельности учителя |
Создать условия для приведения в систему знаний учащихся по изученной теме, для формирования у учащихся четкого понимания того, когда в задаче нужно применить признак параллельности двух прямых, а когда – свойство параллельных прямых; для подготовки к контрольной работе |
||
|
Термины и понятия |
Параллельные прямые, аксиома, свойства параллельных прямых |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию |
Познавательные: владеют логическими действиями. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки, осуществляют контроль по результату и способу действия на уровне произвольного внимания и вносят необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные |
• Тест. • Задания для домашней работы |
||
|
I этап. Активизация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Систематизировать |
(Ф/И) 1. Ответить на вопросы по домашнему заданию. 2. Решить тест (каждое из заданий № 1, 2 оценивается в 4 балла). 1) Выберите верные утверждения. а) Параллельные лучи лежат на параллельных прямых. б) Если накрест лежащие углы равны, то прямые параллельны. в) Если при пересечении двух прямых секущей соответственные углы равны 122°, то прямые параллельны.
2. По данным рисунка докажите, что прямые с и а параллельны.
Ответ: 1) а, б, в |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Тестовые задания |
||
|
Совершенствовать |
(Ф/И) Решить тест с самопроверкой (см. Ресурсный материал) |
||
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И). – Оцените свою работу на уроке. – Составьте синквейн к уроку |
1. Дано: АС || BD, CK || DM, ÐACK = 48°, ÐCDK в 3 раза больше ÐЕDМ. Найти:ÐKDE.
2. Дано: АЕ – биссектриса ∆АВС, AD = DE, AE = ЕС, ÐАСВ = 37°.
|
||
Ресурсный материал
Тест
Часть 1
![]() А1. На рисунке 1 секущей является прямая…
А1. На рисунке 1 секущей является прямая…
а) а; б) с; в) b; г) а или с.
Рис. 1
А2. Для угла 4 накрест лежащим будет угол…
а) 2; б) 5; в) 6; г) 7.
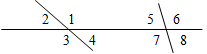
Рис. 2
А3. На рисунке 3 углы 1 и 2 являются…
а) односторонними; в) соответственными;
б) накрест лежащими; г) смежными.
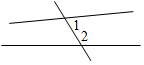
Рис. 3
А4. Дан равносторонний треугольник BCD. Через вершину D провести прямых, параллельных прямой ВС…
а) можно две; в) нельзя ни одной;
б) можно бесконечное множество; г) можно одну.
А5. На рисунке 4 Ð1 = 54°. Прямые а и b будут параллельными, если Ð2 равен…
а) 54°; б) 54° или 126°; в) 126°; г) 36°.
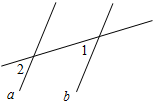
Рис. 4
А6. Прямые будут параллельными на рисунке:
а) 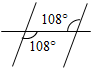 в)
в) 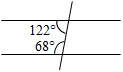
б) 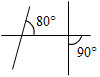 г)
г)
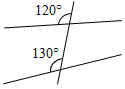
Рис. 5
А7. На рисунке а, b, с пересечены секущей d. Параллельными прямыми будут прямые…
а) а и b; б) b и с; в) а и с; г) а, b и с.
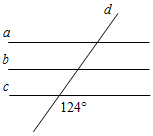
Рис. 6
А8. Верным является высказывание:
а) Если две параллельные прямые пересечены третьей, то сумма накрест лежащих углов равна 180°.
б) Если при пересечении двух прямых секущей накрест лежащие углы в сумме составляют 180°, то прямые параллельны.
в) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
г) Если две прямые параллельны третьей прямой, то они перпендикулярны.
Часть 2
В1. Прямые а и b, изображенные на рисунке, являются ______________________________________________
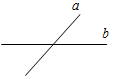
Рис. 7
В2. Из всех углов, изображенных на рисунке, односторонними углами являются углы _____________________
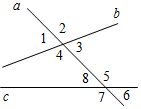
Рис. 8
В3. На рисунке Ð1 = 135°, Ð2 = 45°. Тогда прямые т и п будут ________________________________________
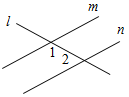
Рис. 9
В4. На рисунке а || b, Ð3 = 108°. Тогда Ð1 = ________________________________________________________
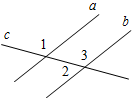
Рис. 10
В5. На рисунке а || b, Ð1 на 50° меньше Ð3. Тогда Ð2 = _______________________________________________
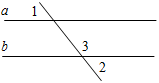
Рис. 11
В6. На рисунке прямые а и b – параллельны, Ð1 = 80°, Ð3 = 50°. Тогда Ð2 = _____________________________
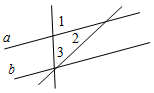
Рис. 12
В7. На рисунке через вершину С треугольника BCD проведена прямая KL, параллельная стороне треугольника BD. При этом ÐBCK = 56°, ÐDCL = 64°. Тогда средним углом треугольника будет угол ______________________
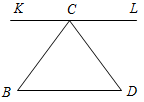
Рис. 13
Часть 3
С1. Отрезок DМ – биссектриса треугольника CDE. Через точку М проведена прямая, пересекающая сторону DE в точке N так, что DN = MN. Вычислите градусные меры углов треугольника DМN, если ÐCDE = 76°.
Ответы:
Часть 1
|
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
А8 |
|
в |
б |
а |
г |
а |
а |
г |
в |
Часть 2
|
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
|
Пересекающимися |
3 и 5, 4 и 8 |
Параллельными |
108° |
65° |
30° |
ÐС = 60° |
Часть 3
С1. Возможный вариант оформления решения задачи.
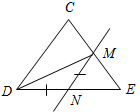
1) DМ – биссектриса треугольника, поэтому ÐCDМ = ÐМDЕ = 38°.
2) DN = MN, поэтому треугольник DNМ является равнобедренным, а значит, ÐМDN = ÐDМN = 38°.
3) Углы DМN и CDМ являются накрест лежащими углами при прямых CD и МN и секущей DМ, а так как внутренние накрест лежащие углы при прямых CD и МN и секущей DМ равны, то прямые DC и МN будут параллельны.
4) Углы CDN и МND являются односторонними при параллельных прямых CD и МN и секущей DЕ, поэтому сумма углов равна 180°. А значит, ÐDNМ = 180° – 76° = 104°.
5) Таким образом, углы треугольника DNМ будут равны 104°, 38°, 38°.
Урок38. Решение задач
|
Цель деятельности учителя |
Создать условия для подготовки к контрольной работе |
|||
|
Термины и понятия |
Параллельные прямые, аксиома, свойства параллельных прямых |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию |
Познавательные: осуществляют логические действия. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки, осуществляют контроль по результату и способу действия на уровне произвольного внимания и вносят необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
|||
|
Образовательные |
• Задания для парной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить правильность выполнения |
1. Ответить на вопросы учащихся по домашнему заданию и проверить правильность решения задач. 1) Так как AC || BD, CK || DM, то ÐACK = ÐВDМ = 48°. ÐCDK + ÐЕDМ = 180° – ÐВDМ. ÐСDK в 3 раза больше ÐЕDМ, тогда 3ÐЕDM + ÐЕDМ = 180° – 48°, 4ÐEDM = 132°, ÐEDM = 33°. Тогда ÐKDЕ = 48° + 33° = 81°.
Рис. 1 Ответ: ÐKDE = 81°. 2) АD = DЕ, тогда ÐDАЕ = ÐDEA. AC – биссектриса ∆ABC, тогда ÐDAE = ÐЕАC, значит, ÐEAC = ÐDEA, следовательно, DE || АС. ∆АЕС – равнобедренный (АЕ = ЕС), тогда ÐEAC = ÐАСЕ = 37°, следовательно, ÐDAC = 74°. DЕ || АС, ÐDАС = 74°, тогда ÐВDЕ = 74°.
Рис. 2 Ответ: ÐBDE = 74°. |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать |
(П) Предлагает учащимся решить пробный вариант контрольной работы. 1. Дано:Ð1 + Ð2 = 88°, а || b. Найти: все углы, образовавшиеся, при пересечении прямых а и b и секущей с.
Рис. 3 2. Дано:Ð1 + Ð2 = 180°, Ð3 = 48°. Найти:Ð4, Ð5, Ð6.
Рис. 4 3. Отрезок DM – биссектриса ∆CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DNM, если ÐCDE = 68°.
4. Прямая ЕK является секущей для АВ и CD (ЕÎАВ, KÎCD). ÐAEK = 49°. При какой величине ÐСKЕ прямые АВ и CD могут быть параллельными? |
1. а || b, тогда Ð1 = Ð2 = 44° (как
накрест лежащие углы при параллельных прямых а и b и секущей с);
Ð3 = Ð4 (как накрест лежащие); Ð1
= Ð3 – смежные, следовательно, Ð3
= Ð4 = 180° – 44° =
2. Ð1 и Ð2
– внутренние односторонние углы и по условию
CD || MN, тогда ÐNDC + ÐDNM = 180°. Значит, ÐDNM = 180° – ÐNDC = 112°.
Рис. 5 Ответ: ÐNDM = ÐNMD = 34°, ÐDNM = 112°. 4.
а) Рис. 6 б) Возможны два случая: а) ÐАЕK = ÐCKЕ, ÐСKЕ = 49°, так как АВ || CD. б) ÐАЕK + ÐСKЕ = 180°, так как АВ || СD, тогда ÐCKE = 131° |
||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Продолжите фразы: • Я научился… • Я понял… • Я смогу… |
(И) Домашнее задание: повторить теоретический материал, подготовиться к контрольной работе |
|||
Урок39. Контрольная работа № 3
|
Цель деятельности учителя |
Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала |
||
|
Термины и понятия |
Признаки параллельности прямых; свойства параллельных прямых |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость изучения предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные |
• Задания для контрольной работы |
||
|
I этап. Выполнение контрольной работы |
|||
|
Цель деятельности |
Задания для контрольной работы |
||
|
Проверить знания, по изученной теме |
(И) Учащиеся выполняют контрольную работу (см. Ресурсный материал) |
||
|
II этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Что выполняли на уроке? – Какие задания вызвали затруднения? Почему? – Как оцениваете свою работу на уроке? |
(И) Домашнее задание: повторить пункты 5–29 |
||
Ресурсный материал
Контрольная работа
![]() Вариант
I
Вариант
I
1. Дано: а || b, с – секущая, Ð1 + Ð2 = 102°.
Найти: все образовавшиеся углы.
![]()
2. Дано:Ðl = Ð2, Ð3 = 120°.
Найти:Ð4.
3. Отрезок AD – биссектриса треугольника ABC. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника ADF, если ÐВАС = 72°.
4*. Прямая ЕK является секущей для прямых CD и MN (ЕÎCD, K ÎMN). ÐDEK равен 65°. При каком значении угла NKE прямые CD и MN могут быть параллельными?
Вариант II
![]() 1. Дано: а || b, с – секущая, Ð1 – Ð2 = 102°.
1. Дано: а || b, с – секущая, Ð1 – Ð2 = 102°.
Найти: все образовавшиеся углы.
![]()
2. Дано:Ð1 = Ð2, Ð3 = 140°.
Найти:Ð4.
3. Отрезок АK – биссектриса треугольника САЕ. Через точку K проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если ÐСАЕ = 78°.
4*. Прямая MN является секущей для прямых АВ и CD (МÎАВ, NÎCD). Угол AMN равен 75°. При каком значении угла CNM прямые АВ и CD могут быть параллельными?
Урок40. Сумма углов треугольника
|
Цель деятельности учителя |
Создать условия для доказательства теоремы о сумме углов треугольника, следствия из нее; для введения понятий остроугольного, прямоугольного и тупоугольного треугольников; для рассмотрения задачи на применение доказанных утверждений |
|
|
Термины и понятия |
Треугольник, противолежащий угол, противолежащая сторона, прилежащий угол и сторона, остроугольный треугольник, тупоугольный, прямоугольный треугольник |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев; умеют отличать гипотезу от факта. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют критичность мышления |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Чертежи к задачам |
|
|
I этап. Анализ результатов контрольной работы |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проанализировать |
(Ф/И) 1. Проанализировать характерные ошибки, допущенные в контрольной работе. 2. Выполнить работу над ошибками |
|
|
II этап. Учебно-познавательная деятельность |
||
|
Цель деятельности |
Постановка учебной задачи |
|
|
Подготовить к восприятию нового материала |
(И) Решение задач по готовым чертежам. Учащимся дается 2–3 минуты на обдумывание, а затем обсуждаются возможные варианты решений. 1) Дано: AF || BD, AB = BF, ÐB = 30°. 2) Дано: DE || AC. Доказать: BD – биссектриса ÐCBF. Найти: сумму углов ∆АВС. Найти:ÐA, ÐF, сумму углов ∆ABF.
Рис. 1 Рис. 2 (Ф) После решения данных задач учитель задает вопрос, в обсуждении которого должен участвовать весь класс. – Случайно ли сумма углов треугольника АВС оказалась равной 180°, или этим свойством обладает любой треугольник? (У каждого треугольника сумма углов равна 180°.) – Это утверждение носит название теоремы о сумме углов треугольника. Итак, тема сегодняшнего урока – «Сумма углов треугольника» |
|
|
III этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Доказать теорему |
(Ф) 1. Доказательство теоремы о сумме углов треугольника (рис. 125 учебника). 2. Решение задач № 223 (а, б, г), 225, 226 (устно). 3. Перед введением классификации треугольников по углам (п. 31) учащимся задается вопрос: «Может ли треугольник иметь: а) два прямых угла; б) два тупых угла; в) один прямой и один тупой угол?». Ответы должны быть обоснованы с помощью теоремы о сумме углов треугольника. 4. Запись в тетрадях вывода из данных ответов (следствие из теоремы о сумме углов треугольника): в любом треугольнике либо все три угла острые, либо два угла острые, а третий – тупой или прямой. 5. Ввести понятия остроугольного, тупоугольного и прямоугольного треугольников и обратить внимание учащихся на названия сторон прямоугольного треугольника – гипотенуза и катет (рис. 126 учебника, модели треугольников) |
|
|
IV этап. Решение задач на закрепление изученного материала |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
При решении простейших задач отработать применение изученной теоремы |
(Ф/И) Организует деятельность учащихся. 1. Решить задачи № 227 2. Решить задачу № 228 (а, в) на доске и в тетрадях. 3. Решить задачу № 229 |
№ 227. а) Дано:DАВС, АВ = ВС, ÐА>ÐВв 2 раза. Найти:ÐА, ÐВ, ÐС.
Рис. 3 Решение: Примем ÐВ = х°, следовательно, ÐА = ÐС = 2х°. Так как ÐА + ÐВ + ÐС = 180°, то 2х + х
+ 2х = 180°, тогда 5х = 180°, ÐВ = 36°, ÐА = ÐС = 72°. б) Дано:DАВС, АВ = ВС, ÐС <ÐBCD в 3 раза. Найти:ÐА, ÐВ, ÐС.
Рис. 4 Решение: Примем ÐС = х°, следовательно,
ÐА = х°, ÐBCD = 3х°. Так как ÐBCD = ÐА + ÐВ + ÐС = 180°, тогда: х + 2х + х = 180°, 4х = 180°, х = 45°. ÐА = ÐС = 45°, ÐВ = 90°. № 224. Дано:DАВС, ÐА : ÐВ : ÐС = 2 : 3 : 4. Найти:ÐА, ÐВ, ÐС.
Рис. 5 Решение: Примем 1 часть – х°, следовательно, ÐА = 2х°, ÐВ = 3х°, ÐС = 4х°. Так как ÐА + ÐВ + ÐС = 180°, то 2х + 3х + 4х = 180°, тогда: 9х = 180°, х = 20°. 20° приходится на 1 часть. ÐА = 2 · 20° = 40°, ÐВ = 3 · 20° = 60°, ÐС = 4 · 20° = 80°. Ответ: 40°, 60°, 80°. № 228. 1) Рассмотрим два случая: а) Угол при основании равен
40°, тогда второй угол при основании равнобедренного треугольника тоже равен
40°; значит, угол при вершине равен б) Угол при вершине равен
40°, тогда углы при основании равны Ответ: 40°, 40°, 100° или 40°, 70°, 70°. 2) Опираемся на доказанное в задаче № 226 утверждение: углы при основании равнобедренного треугольника острые. Значит, угол при вершине равен 100°, а углы при основании равны (180° – 100°) : 2 = 40°. Ответ: 100°, 40° и 40°. № 229. Дано:DАВС, АВ = ВС, AD – биссектриса ÐА, ÐС = 50°. Найти:ÐАDС.
Рис. 6 Решение: 1) Так как DАВС – равнобедренный, то ÐА = ÐС = 50°. 2) Так как AD – биссектриса ÐА, то ÐВAD = ÐDАС = 25°. 3) Рассмотрим DАDС: ÐDАС + ÐАDС + ÐС = 180°, тогда: 25° + ÐАDС + 50° = 180°, ÐАDС = 180° – 75°, ÐАDС = 105°. Ответ: 105° |
|
V этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Что нового узнали на уроке? – Составьте синквейн к уроку |
(И)Домашнее задание: изучить
пункты 30–31; ответить на вопросы 1, 3, 4, 5 |
|
Урок 41. Внешний угол треугольника.
Теорема о внешнем угле треугольника
|
Цели деятельности |
Создать условия для закрепления знаний учащихся о сумме углов треугольника при решении задач, введения понятия внешнего угла треугольника, доказательства теоремы о внешнем угле треугольника, обучения решению задач |
|
|
Термины и понятия |
Треугольник, внешний угол, смежный угол |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий, умеют формулировать и доказывать теорему о внешнем угле треугольника |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Чертежи к задачам. • Задания для самостоятельной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить уровень сформированности теоретических знаний |
(Ф/И) 1. Один учащийся на доске доказывает теорему о сумме углов треугольника. 2. Второй учащийся решает на доске задачу из домашнего задания № 230. 3. Весь класс решает задачи по готовым чертежам (устно). – Вычислите все неизвестные углы треугольников.
Рис. 1 Рис. 2 Рис. 3 Рис. 4 Рис. 5
Рис. 6 Рис. 7 Рис. 8 |
|
|
II этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Ввести понятие внешнего угла и доказать сопутствующую теорему |
(Ф/И) 1. Ввести понятие внешнего угла треугольника. 2. Доказать теорему о внешнем угле треугольника (рис. 125 учебника). 3. Решить задачу (устно). В треугольнике АВС ÐВ = 110°. Чему равны: а) сумма остальных внутренних углов треугольника; б) внешний угол при вершине В? 4. По готовому чертежу на доске устно решить задачу. Найдите внутренние углы и внешний угол СDF треугольника KСD
Рис. 9 |
|
|
III этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
При решении простейших задач отработать изученный материал |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 232 под
руководством учителя на доске 2. Рассмотреть обратное утверждение: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основании. Действительно, этот внешний угол равен сумме двух углов при основании равнобедренного треугольника, а так как углы при основании равны, то данный внешний угол в два раза больше угла при основании треугольника. 3. Решить задачу № 234 на доске и в тетрадях (рассмотреть два случая) |
№ 232. Дано:DАВС, ÐВСD>ÐА в 2 раза. Доказать:DАВС – равнобедренный.
Рис. 10 Доказательство: Примем ÐА = х, тогда ÐВСD = 2х. По свойству внешнего угла: ÐВСD = ÐА + ÐВ, тогда 2х = х + ÐВ, тогда ÐВ = х, значит, ÐА = ÐВ, то есть DАВС – равнобедренный. Обратное утверждение верно. № 234. Дано:DАВС, АВ = ВС, ÐВСD = 115°. Найти:ÐА, ÐВ, ÐС.
Рис. 11 Решение: 1) ÐС, ÐВСD – смежные, значит, ÐС = 180° – 115° = 65°. 2) ÐА = ÐС = 65° (по свойству равнобедренного треугольника). 3) ÐВ = 180° – (ÐА + ÐС). ÐВ = 180° – 130° = 50°. Ответ: 65°, 65°, 50°. Дано:DАВС, АВ = ВС, ÐСВD = 115°. Найти:ÐА, ÐВ, ÐС.
Рис. 12 Решение: 1) ÐВ, ÐСВD – смежные, значит, ÐВ = 180° – 115° = 65°. 2) Так как ÐА = ÐС (по свойству
равнобедренного треугольника), Ответ: 65°, 57°30¢, 57°30¢ |
|
IV этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Совершенствовать навыки самостоятельного решения задач |
(И) Работа выполняется 15–20 минут. Вариант I 1. Один из углов равнобедренного треугольника равен 96°. Найдите два других угла треугольника. 2. В треугольнике СDЕ с углом ÐЕ = 32° проведена биссектриса CF, ÐСFD = 72°. Найдите ÐD. Вариант II 1. Один из углов равнобедренного треугольника равен 108°. Найдите два других угла треугольника. 2. В треугольнике СDЕ проведена биссектриса CF, ÐD = 68°, ÐЕ = 32°. Найдите ÐСFD. Вариант III 1. В равнобедренном треугольнике MNP c основанием МР и углом ÐN = 64° проведена высота МН. Найдите ÐРМН. 2. В треугольнике СDЕ
проведены биссектрисы CK и DР, пересекающиеся в точке F,
причем ÐDFK = 78°. Вариант IV 1. В равнобедренном треугольнике CDЕ c основанием СЕ и ÐD = 102° проведена высота СН. Найдите ÐDСН. 2. В треугольнике АВС
проведены биссектрисы АМ и ВN, пересекающиеся в точке K,
причем ÐАKN = 58°. |
|
|
V этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какой угол называется внешним углом треугольника? – Каким свойством обладает внешний угол равнобедренного треугольника? – Оцените свою работу на уроке. Поставьте себе оценку. Какие затруднения у вас возникли? |
(И)Домашнее задание: изучить
пункты 30–31; ответить на вопросы 1–5 |
|
Урок 42. Теорема о соотношениях
между сторонами и углами треугольника
|
Цель деятельности учителя |
Создать условия для рассмотрения теоремы о соотношениях между сторонами и углами треугольника, следствия из этих теорем; для обучения применению этих знаний при решении задач |
|
|
Термины и понятия |
Треугольник, противолежащий угол, сторона |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Чертежи к задачам |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Провести анализ ошибок, допущенных в самостоятельной работе |
(Ф/И) 1. Анализ результатов самостоятельной работы. 2. Обсуждение вопросов учащихся по домашнему заданию |
|
|
II этап. Учебно-познавательная деятельность |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Рассмотреть теоремы |
(Ф/И) 1. Решить подготовительную задачу. Дано: ∆МОС; KÎМС; KМ = ОМ. Доказать: 1) Ð1 >Ð3; 2) ÐМОС>Ð3.
Рис. 1 Доказательство: 1) Треугольник ОМK – равнобедренный с основанием ОK, поэтому Ð1 = Ð2. Угол 2 – внешний угол треугольника ОKС, поэтому Ð2 >Ð3. Значит, Ð1 = Ð2 и Ð2 >Ð3, следовательно, Ð1 >Ð3. 2) Так как точка K лежит на МС, то ÐМОС>Ð1, а так как Ð1 >Ð3, то ÐМОС>Ð3. 2. Сформулировать и доказать первое утверждение теоремы: в треугольнике против большей стороны лежит больший угол (по рис. 127 учебника). 3. Решить задачу № 236 (устно). 4. Перед доказательством второго утверждения теоремы (в треугольнике против большего угла лежит бо́льшая сторона) напомнить учащимся, какая теорема называется обратной данной, и предложить привести примеры обратных теорем, изученных ранее. 5. Сформулировать утверждение, обратное первому утверждению (самостоятельно). 6. Доказать обратное утверждение (методом от противного). После того как
сформулирована обратная теорема, записаны ее условие и заключение, полезно
вспомнить, 7. Решить задачу № 237 (устно). 8. Доказать следствие 1 (самостоятельно). 9. Доказать следствие 2, выражающее признак равнобедренного треугольника (с помощью учителя) |
|
|
III этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Научить применять |
(Ф/И) 1. Решить задачи по готовым чертежам.
Рис. 2 Рис. 3 Рис. 4 Рис. 5 1) Дано:ÐA = ÐВ(рис. 2). Доказать: ∆АВС – равнобедренный. 2) Сравните углы ∆АВС(рис. 3). 3) Укажите наибольшую и наименьшую стороны ∆АВС (рис. 4). 4) Сравните отрезки AD и DC (рис. 5). 2. Решить задачу № 240 на доске и в тетради. № 240. Дано:DАВС, АВ = ВС, АО – биссектриса ÐА, СО – биссектриса ÐС. Доказать:DАОС – равнобедренный.
Рис. 6 Доказательство: 1) Так как DАВС – равнобедренный, то ÐА = ÐС. 2) Так как АО, СО – биссектрисы соответственно равных углов, то Ð1 = Ð2 = Ð3 = Ð4. 3) Рассмотрим DАОС: Ð2 = Ð3, тогда АО = СО, значит, DАОС – равнобедренный по определению |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какие теоремы изучены на уроке? – Оцените свою работу на уроке. – Задайте три вопроса по теме урока |
(И) Домашнее задание: изучить п. 33; ответить на вопросы 6–8 на с. 88; решить задачи № 239, 241 |
|
Урок43. Теорема о соотношениях
между сторонами и углами треугольника.
Решение задач
|
Цель деятельности учителя |
Создать условия для рассмотрения теоремы о соотношениях между сторонами и углами треугольника, следствия из этих теорем; для обучения применению полученных знаний при решении задач |
|
|
Термины и понятия |
Треугольник, противолежащий угол, сторона |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для проверочной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить уровень |
(Ф/И) 1. Проверить правильность выполнения домашнего задания. 2. Провести проверочную работу (см. Ресурсный материал) |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать |
(Ф/И) Организует деятельность
учащихся: решение задач № 243, 246 у доски |
№ 243. Дано:DАВС, АА1 – биссектриса ÐА, СD || АА1, СDÇАВ = D. Доказать: АС = AD.
Рис. 1 Доказательство: 1) Так как СD || АА1,
то Ð1 = Ð3 (как соответственные), с другой стороны, 2) В DСАD: Ð3 + ÐСАD + Ð4 = 180° (свойство углов треугольников). Сравним два равенства и получим, что Ð4 = Ð2. 3) Ð1 = Ð2 (по
усл.), Ð1 = Ð3 (из п. 1), Ð2 = Ð4 (из п. 2), Ð3 = Ð4, значит, № 246. Дано:DАВС, ВО и ОС – биссектрисы, ОЕ || АВ, ОD || АС. Доказать:РОЕD = BC.
Рис. 2 Доказательство: 1) Так как ОЕ || АВ, то Ð1 = Ð3, как накрест лежащие, Ð1 = Ð2, так как ВО – биссектриса, Ð2 = Ð3, тогда ВЕ = ОЕ (свойство равнобедренного треугольника). 2) Так как ОD || АС, то Ð4 = Ð6, как накрест лежащие, Ð4 = Ð5, так как СО – биссектриса, Ð5 = Ð6, значит, CD = ОD (свойство равнобедренного треугольника). РОЕD = ОЕ + ЕD + DО || || || тогда РОЕD = BC, что и требовалось доказать ВС = ВЕ + ЕD + DС |
|
III этап. Итоги урока |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Оцените свою работу на уроке. – Задайте три вопроса по теме урока |
(И) Домашнее задание: решить задачи № 244, 245 |
|
Ресурсный материал
Проверочная работа
1. Сумма углов треугольника равна:
а) 360°; б) 180°; в) 270°; г) 90°.
2. На каком из рисунков изображен внешний угол треугольника?

а) б) в) г)
3. Если три угла треугольника острые, то треугольник называется …
4. Если один из углов треугольника тупой, то треугольник называется …
5. Если один из углов треугольника прямой, то треугольник называется …
Сторона такого треугольника, лежащая против прямого угла, называется … а две другие стороны – …
6. Впишите названия сторон ΔАВС.
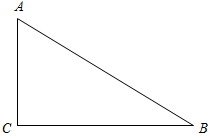
7. Чему равен ÐС в DАВС, если ÐВ = 57°, ÐА = 65°?
а) 58°; б) 148°; в) 238°; г) 78°.
8. В треугольнике против большей стороны лежит … угол; против большего угла лежит … сторона.
9. Из приведенных ниже утверждений выберите верные:
а) Каждая сторона треугольника больше суммы двух других сторон.
б) Каждая сторона треугольника равна сумме двух других сторон.
в) Каждая из сторон треугольника меньше суммы двух других сторон.
г) Для каждого из треугольников справедливы разные утверждения из приведенных выше.
Урок44. Неравенство треугольника
|
Цели деятельности учителя |
Создать условия для доказательства теоремы о неравенстве треугольника, для обучения решению задач с опорой на изученные теоремы и следствия из них; способствовать развитию логического мышления учащихся |
|
|
Термины и понятия |
Треугольник, противолежащий угол, сторона, неравенство треугольника |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для фронтальной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать теоретический материал |
(Ф/И) 1. Проверка усвоения изученного на предыдущем уроке материала. Фронтальный опрос. 2. Двое учащихся записывают на доске решения задач домашнего задания для последующей проверки с классом |
|
|
II этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Доказать теорему о неравенстве треугольника |
(Ф/И) 1. Доказательство теоремы о неравенстве треугольника (проводится учителем). 2. Решение задачи № 251 (см. на с. 75 учебника). После этого записать в
тетрадях вывод: Каждая сторона треугольника меньше суммы двух других
сторон, 3. Решение задачи № 248 (устно) |
|
|
III этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Учить решать задачи,
используя изученные |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 249. 2. Решить задачу № 250 (а) (самостоятельно). 3. Решить задачу № 253 на доске и в тетрадях |
№ 249. Дано:DАВС, АВ = ВС, а = 25 см, b = 10 см. Найти: какая из сторон является основанием?
Рис. 1 Решение: АС = 10 см, так как по неравенству треугольника АВ + ВС>АС,
25 + 25 > № 253. Дано:DАВС, АВ = ВС, РАВС = 25 см, АС – АВ = 4 см, ÐDВС – острый. Найти:АВ, ВС, АС.
Рис. 2 Решение: 1) Примем АВ = ВС = х см, следовательно, АС = х + 4 см. Так как РАВС = АВ + ВС + АС, то 25 = х + х + х + 4; 21 = 3х; х = 7. АВ = ВС = 7 см, следовательно, АС = 11 см |
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – При каком условии существует треугольник? – Составьте синквейн к уроку |
(И) Домашнее задание:
выучить материал пунктов 30–34; ответить |
|
Урок45. Решение задач.
Подготовка к контрольной работе
|
Цели деятельности учителя |
Совершенствовать навыки решения задач; создать условия для подготовки учащихся к предстоящей контрольной работе |
|
|
Термины и понятия |
Треугольник, противолежащий угол, сторона, неравенство треугольника |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют работать с геометрическим текстом, точно и грамотно
выражать свои мысли в устной и письменной речи |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Задания для фронтальной, самостоятельной работы. • Чертежи к задачам |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить уровень сформированности теоретических знаний |
(Ф/И) 1. Доказательство теоремы о соотношениях между сторонами и углами треугольника и теоремы о неравенстве треугольника. (Выполняют учащиеся у доски и за первыми партами – на листках. По окончании работы листки собрать и выслушать ответы учеников.) 2. Фронтальная работа с классом: 1) Ответить на вопросы 1–9 на с. 88. 2) Устно решить задачу. Существует ли треугольник со
сторонами 4 м, 5 м и 8 м; со сторонами 6 см, 12 см и 3 см; со сторонами 9 дм,
|
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
(Ф/И) 1. Решение задач по готовым чертежам. 1) Может ли длина АВ быть равной 27 см?
Рис. 1 2) Дано: R1 = 5 cм, R2 = 4 см. Каким может быть расстояние от точки О1 до точки О2?
Рис. 2 3) Доказать:ÐABС>ÐC. 4) Сравнить АС и ВС.
Рис. 3 Рис. 4 5) Доказать: ВС<ВМ<ВА. 6) Доказать: BD + DС>AD.
Рис. 5 Рис. 6 2. Решение задачи (один ученик решает у доски, остальные – в тетрадях). Дано: отрезок ЕK – биссектриса треугольника DEC. Доказать:KС<ЕС.
Рис. 7 Доказательство: ÐЕKС – внешний угол ∆DKE, значит, он больше Ð1, следовательно, ÐEKС>Ð2 (Ð1 = Ð2, так как ЕK – |
|
|
III этап. Самостоятельная работа |
||
|
Цель деятельности |
Задание для самостоятельной работы |
|
|
Проверить умение применять полученные знания при решении задач |
(И) Выполняют задания самостоятельной работы (см. Ресурсный материал) |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какие теоремы использовались при решении задач? – Оцените свою работу на уроке. – Какие трудности возникли у вас при решении задач? |
(И) Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 17–34; решить задачи № 244, 252, 297 |
|
Ресурсный материал
Самостоятельная работа
1. Дано:ÐBAE = 112°, ÐDBF = 68°, ВС = 9 см. 2. Дано:ÐCBM = ÐACF, РАВС = 34 см, ВС = 12 см.
Найти: АС. Найти: АВ.
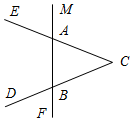
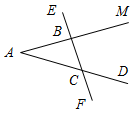
Рис. 1 Рис. 2
3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
4. В равнобедренном треугольнике биссектрисы углов при основании образуют при пересечении угол, равный 52°. Найдите угол при вершине этого треугольника.
5. В треугольнике ABCÐB = 70°, ÐC = 60°. Сравните стороны треугольника.
6. Дано:ÐC = 90°, ÐB = 27°, CD – высота ∆ABC, СK – биссектриса ∆АВС.
Найти:ÐDCK.
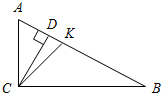
Рис. 3
Ответы и указания к задачам для самопроверки:
1. АС = 9 см, так как ∆АВС – равнобедренный (ÐABC = ÐBAС).
2. АВ = 11 см, так как ∆АВС – равнобедренный с основанием ВС (ÐABC = ÐACB).
3. 20 см, 20 см, 37 см.
4. Решение (см. рис. 4):
ÐAOC ≠ 52°, тогда Ð1 + Ð 2 = 128° и Ð3 + Ð4 = 128°, a ÐВАС + ÐВСА = 256°, чего быть не может, значит, ÐАОС1 = 52°, тогда Ð1 + Ð2 = 52°, Ð3 + Ð4 = 52°, a ÐВAC + ÐВСА = 104°, значит, ÐАВC = 76°.
Ответ: ÐABC = 76°.
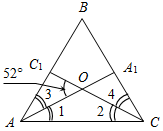
Рис. 4
5. ÐВ = 70°, ÐC = 60°, тогда ÐA = 50°. Следовательно, по теореме о соотношениях между сторонами и углами треугольника, ВС<АВ <АС.
Ответ: ВС<АВ<АС.
6. ÐACK = 45°, ÐBAC = 63°, тогда ÐАСD = 27°, ÐDCK = ÐАСK – ÐАСD = 45° – 27°= 18°.
Ответ: ÐDCK = 18°.
Урок46. Контрольная работа № 4
|
Цель деятельности учителя |
Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала |
|
|
Термины и понятия |
Треугольник, неравенство треугольника, соотношения между сторонами и углами треугольника |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость изучения предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для контрольной работы |
|
|
I этап. Выполнение контрольной работы |
||
|
Цель деятельности |
Задания для контрольной работы |
|
|
Проверить уровень усвоения изученного материала, развития навыков решения задач |
(И) Выполняют задания контрольной работы (см. Ресурсный материал) |
|
|
II этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Что выполняли на уроке? – Какие задания вызвали затруднения? Почему? – Как оцениваете свою работу на уроке? |
(И) Домашнее задание: повторить названия сторон прямоугольного треугольника |
|
Ресурсный материал
Контрольная работа
Вариант I
1. На рисунке 1 ÐАВЕ = 104°, ÐDСF = 76°, АС = 12 см. Найдите сторону АВ треугольника АВС.
2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем ÐСМD острый. Докажите, что DЕ >DМ.
3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
Вариант II
1. На рисунке 2 ÐВАЕ = 112°, ÐDВF = 68°, ВС = 9 см. Найдите сторону АС треугольника АВС.
2. В треугольнике MNP точка K лежит на стороне MN, причем ÐNKP острый. Докажите, что KР <МР.
3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
Вариант III
(для более подготовленных учащихся)
1. На рисунке 1 ÐСВМ = ÐАСF; РАВС= 34 см, ВС = 12 см. Найдите сторону АС треугольника АВС.
2. В треугольнике MNK ÐK = 37°, ÐМ = 69°, NP – биссектриса треугольника. Докажите, что МР <РK.
3. Периметр равнобедренного треугольника равен 45 см, а одна из его сторон больше другой на 12 см. Найдите стороны треугольника.
Вариант IV
(для более подготовленных учащихся)
1. На рисунке 2 ÐЕАМ = ÐDВF; ВС = 17 см, РАВС= 45 см. Найдите сторону АВ треугольника АВС.
2. В треугольнике СDЕ ÐЕ = 76°, ÐD = 66°, ЕK – биссектриса треугольника. Докажите, что KС >DK.
3. Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см меньше другой. Найдите стороны треугольника.
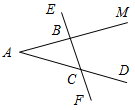
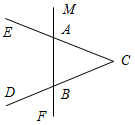
Рис. 1 Рис. 2
Урок47. Анализ ошибок контрольной работы
|
Цели деятельности учителя |
Создать условия для устранения пробелов в знаниях учащихся; совершенствовать навыки решения задач |
|
|
Термины и понятия |
Треугольник, противолежащий угол, сторона, неравенство треугольника |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные |
• Задания для групповой работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Сообщить результаты контрольной работы |
(Ф) 1. Сообщить общие результаты контрольной работы. 2. Объяснить задания, с которыми не справилось большинство учащихся, или заслушать тех, кто успешно справился с этими заданиями. 3. Продемонстрировать лучшие работы |
|
|
II этап. Работа над ошибками |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Устранить пробелы в знаниях учащихся |
(И/Г) 1. Учащиеся находят свои ошибки, используя указания учителя или ученика, справившегося с задачами контрольной работы (можно объединить детей в небольшие группы в зависимости от уровня и варианта контрольной работы, в этом случае им будет легче находить свои ошибки). 2. Учащиеся решают другой
вариант контрольной работы или переходят к решению задач следующего уровня 3. Более подготовленным учащимся можно предложить решить дополнительные задачи. Задача 1. На сторонах угла А,
равного 127°, отмечены точки В и С, а внутри угла – точка D
так, что ÐABD = 25°, Найти угол BDC.
Рис. 1 Задача 2. Треугольники ABC и ADC
имеют общую сторону АС. Отрезок BD пересекает отрезок АС.
Докажите, что ∆ADC является тупоугольным, если ÐABC = 130°.
Рис. 2 Задача 3. В равнобедренном
треугольнике АВС угол В равен 100°. Внутри треугольника взята
такая точка М,
Рис. 3 |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Задайте три вопроса по задачам. – Оцените свою работу. – Какие трудности у вас возникли? |
(И) Домашнее задание: можно предложить учащимся на выбор поменяться вариантами контрольной работы или решить дополнительные задачи |
|
Урок48. Некоторые свойства прямоугольных треугольников
|
Цель деятельности учителя |
Создать условия для рассмотрения свойств прямоугольных треугольников, обучения решению задач на применение свойств прямоугольных треугольников |
|
|
Термины и понятия |
Треугольник, противолежащий угол, катеты, гипотенуза |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные |
• Задания для самостоятельной, групповой работы. • Чертежи к задачам |
|
|
I этап. Мотивация к деятельности |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Подготовить учащихся к
восприятию новой |
(Ф/И) Организует деятельность учащихся. 1. Решить задачи по готовым чертежам. 1) Найти:ÐA, ÐC. 2)
Дано:ÐA : ÐB = 1 : 2. 3) Доказать: AD = Найти:ÐA, ÐB.
Рис. 1 Рис. 2 Рис. 3 |
|
|
II этап. Учебно-познавательная деятельность |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Рассмотреть свойства прямоугольных тре-угольников |
(Ф/И) Можно сформулировать свойства прямоугольного треугольника в виде задач на доказательство и предложить учащимся решить их самостоятельно. (Задачу 1 можно предложить менее подготовленным учащимся, остальных детей разделить на два варианта и предложить варианту I решить задачу 2, варианту II – задачу 3. На решение задачи отводится 5–7 минут. Через 2–3 минуты от начала решения можно дать подсказку для решения задач 2 и 3: достройте свой треугольник до равностороннего с боковой стороной, равной гипотенузе.) Задача 1. Докажите, что в прямоугольном треугольнике сумма острых углов равна 90°. Задача 2. Докажите, что в прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы. Задача 3. Докажите, что если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°. Необходимо заслушать различные способы решения данных задач,
выбрать наиболее рациональный способ |
|
|
III этап. Решение задач на закрепление изученного материала |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Научить применять изученные свойства при решении задач |
(Ф/И) Организует деятельность учащихся. 1. Решить задачи по готовым чертежам на доске (устно). 1) Дано: ∆АВС. Найти: углы ∆АВС.
Рис. 6 2) Дано: а || b. Найти: углы ∆MON.
Рис. 7 2. Решить задачу № 254 3. Решить задачу № 255
4. Решить задачу № 257
(П) 5. Решить задачу № 260
(Г) 6. Решить задачи. Задача 1. Найти углы прямоугольного треугольника, если угол между биссектрисой и высотой, проведенными из вершины прямого угла, равен 15°.
Задача 2. В равнобедренном треугольнике один из углов равен 120°, а основание равно 4 см. Найдите высоту, проведенную к боковой стороне |
№ 254. Дано:DАВС – равнобедренный, ÐС = 90°, ÐА = ÐВ. Найти:ÐА, ÐВ.
Рис. 4 Решение: 1) ÐА + ÐВ = 90° (свойство прямоугольного треугольника), ÐА = ÐВ, следовательно, ÐА = ÐВ = 90° : 2 = 45°. Ответ: 45°, 45°. № 255. Дано:DCDЕ – равнобедренный, CD = DЕ, CF – высота, ÐD = 54°. Найти:ÐЕСF.
Рис. 5 Решение: 1) Так как CD = DЕ, то ÐС = ÐЕ.ÐС + ÐЕ = 180° – ÐD (по свойству суммы углов треугольника); ÐС + ÐЕ = 180° – 54°, ÐС = ÐЕ = 126° : 2 = 63°. 2) ÐFСD = 90° – ÐD (по свойству прямоугольного
треугольника); 3) ÐЕСF = ÐС – ÐFСD, ÐЕСF = 63° – 26° = 37°. Ответ: 37°. № 257. Дано:DАВС, ÐС = 90°, внешний угол при ÐА = 120°, АС + АВ = 18 см. Найти: АС, АВ.
Рис. 8 Решение: 1) По свойству смежных углов, ÐВАС = 180° – 120° = 60°. 2) ÐВ = 90° – ÐА (по свойству прямоугольного
треугольника), ÐВ = 90° – 60° = 3) АС + АВ = 18, АВ = 2АС, тогда АС + 2АС = 18, тогда АС = 6 см. АВ = 2 · 6 = 12 см. Ответ: 6 см, 12 см. № 260. Дано:DАВС – равнобедренный, АВ = ВС = 15,2 см, ВВ1 – высота, ВВ1 = 7,6 см. Найти: углы DАВС.
Рис. 9 Решение: 1) ВВ1 = 2) Так как DАВС – равнобедренный, то ÐВАС также 30°, а ÐАВС = 180° – Ответ: 30°, 30°, 120°.
Задача 1.
Рис. 10 Решение: CD – биссектриса, СН – высота, ÐDCH = 15°, ÐDCA = 45°, тогда ÐНСА = 30°. ∆НСА – прямоугольный, в нем ÐНСА = 30°, тогда ÐСАН = 60°. ∆АВС – прямоугольный, в нем ÐA = 60°, тогда ÐВ = 30°. Ответ: 30°, 60°, 90°. Задача 2.
Рис. 11 Решение: 120° – угол при вершине равнобедренного треугольника, тогда ÐA = ÐC = 30°. АН – высота ∆АВС, тогда ∆АНС –
прямоугольный, в нем ÐC = 30°, значит, Ответ: 2 см |
|
IV этап. Итоги урока |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какие свойства прямоугольных треугольников узнали на уроке? – Оцените свою работу на уроке и работу своих товарищей в группе |
(И) Домашнее задание: выучить материал пунктов 30–35; ответить на вопросы 1–9 на с. 88; решить задачи № 242, 250 (б, в) |
|
Урок49. Некоторые свойства прямоугольных треугольников.
Решение задач
|
Цели деятельности учителя |
Создать условия для закрепления основных свойств прямоугольных треугольников, рассмотрения признака прямоугольного треугольника и свойства медианы прямоугольного треугольника; совершенствовать навыки решения задач на применение свойств прямоугольного треугольника |
|
|
Термины и понятия |
Треугольник, противолежащий угол, катеты, гипотенуза |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные |
• Задания для фронтальной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить теоретическую подготовленность учащихся |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Заполнить пропуски в решении задач. 1) В равнобедренном треугольнике один из внешних углов равен 60°, высота, проведенная к боковой стороне, равна 5 см. Найдите основание треугольника.
Рис. 1 Решение: Так как внешний угол равен
60°, то смежный с ним внутренний угол равен ... Этот угол может быть только
углом, противолежащим основанию, так как он ... Так как ∆АВС –
равнобедренный с основанием AС, Так как АН – высота, то ∆АНС – ... В ∆АНСÐC = 30°, значит, АН = ... Так как АН = 5 см, то АС = ... Ответ: АС = ... 2) Высота и медиана, проведенные из одной вершины треугольника, разделили его угол на три равные части. Найдите углы треугольника.
Рис. 2 Решение: Пусть СН – высота, СМ – медиана ∆АВС, Ð1 = Ð2 = Ð3. Проведем ОМ^СВ, тогда ∆АСН = ∆МСН по ... ∆СМН = ∆СМО по ... Тогда АН = НМ
= МО = Ответ: ÐА = 60°, ÐB = 30°, ÐC = 90°. После обсуждения нужно отметить, что эти две задачи характеризуют дополнительные свойства прямоугольных треугольников: 1) Свойство медианы прямоугольного треугольника, проведенной из вершины прямого угла: В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине гипотенузы. 2) Признак прямоугольного треугольника: Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решение задачи с подробным обсуждением: Гипотенуза прямоугольного треугольника в четыре раза больше проведенной к ней высоты. Найдите острые углы треугольника. (Г) 2. Самостоятельное решение задач с последующей самопроверкой по готовым ответам. 1) Найти: ВС. 2) Найти: АВ.
Рис. 4 Рис. 5 3) Найти: АЕ. 4) Найти:ÐB, ÐD.
Рис. 6 Рис. 7 5) Найти:СЕ, РС. 6) Найти: СА1.
Рис. 8 Рис. 9 7) Найти:ÐMCA. 8) Найти:ÐA, ÐABC.
Рис. 10 Рис. 11 |
1. Рис. 3 Решение: СН – высота. Пусть СН = х, тогда АВ = 4х. Проведем медиану СМ, СМ
= В ∆СНМÐH = 90°, СН = х,
СМ = 2х, тогда ∆АМС – равнобедренный, тогда ÐA = ÐMCA = 15°. ∆ABC – прямоугольный, ÐA = 15°, тогда ÐB = 75°. Ответ: 15°, 75°.
2. Ответы для самопроверки. 1) ВС = 5. 2) АВ = 16. 3) АЕ = 14. 4) ÐВ = ÐD = 60°. 5) СЕ = 4,5, РС = 13,5. 6) СА1 = 10. 7) ÐMCA = 20°. 8) ÐА = 65°, ÐABC = 90° |
|
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Какие свойства прямоугольного треугольника узнали на уроке? – Сформулируйте признак прямоугольного треугольника. – Оцените свою работу в группе. – Какие затруднения возникли? |
(И)Домашнее задание (дано на карточке): решить задачи. 1) Найти:ÐCAD. 2) Найти: AD.
3) Найти: BF. 4) Найти: MD.
|
||
Урок50. Признаки равенства прямоугольных треугольников
|
Цели деятельности |
Создать условия для доказательства признаков равенства прямоугольных треугольников и демонстрации их применения при решении задач |
|
|
Термины и понятия |
Треугольник, противолежащий угол, катеты, гипотенуза |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы, понимать и использовать математические средства наглядности. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для фронтальной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить уровень усвоения теоретического материала |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Сформулировать свойства прямоугольных треугольников. 3. Вспомнить признаки равенства треугольников. 4. Решить задачу. Гипотенузы ВD и АС прямоугольных треугольников ВАD и АВС с общим катетом АВ и с равными катетами АD и ВС пересекаются в точке О. Докажите, что треугольник АОВ равнобедренный.
Рис. 1 5. Заполнить пропуски в решении задачи. Высота и медиана, проведенные из одной вершины треугольника, разделили его угол на три равные части. Найдите углы треугольника. Решение: Пусть СН – высота, СМ – медиана ÐАВС, Ð1 = Ð2 = Ð3. Проведем ОМ^СВ, тогда ∆АСН = ∆МСН по ... ∆СМН = ∆СМО по … Тогда АН = НМ
= МО =
Рис. 2 Ответ: ÐА = 60°, ÐB = 30°, ÐC = 90° |
|
|
II этап. Учебно-познавательная деятельность |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Рассмотреть и доказать
признаки равенства прямоугольных |
(Ф/И) 1. Доказательство признаков равенства прямоугольных треугольников по двум катетам, по катету и прилежащему острому углу, по гипотенузе и острому углу с опорой на признаки равенства треугольников (устно;самостоятельно). 2. Доказательство признака равенства прямоугольных треугольников по гипотенузе и острому углу по моделям равных прямоугольных треугольников (устно). 3. Доказательство признака равенства прямоугольных треугольников по гипотенузе и катету (по рис. 133 учебника) (проводит учитель, так как доказательство этого признака требует дополнительных построений и непростых логических рассуждений) |
|
|
III этап. Учебно-познавательная деятельность |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Научить применять |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 261 на
доске и в тет- 2. Сформулировать и доказать
признак равенства прямоугольных треугольников 3. Решить задачу № 269 на
доске и в тет- 4. Решить задачу. Докажите, что если треугольник прямоугольный, то медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
Рис. 4 Доказательство: DСВМ –
равнобедренный. 5. Решить задачу. Дано: СМ = ВМ = МА. Доказать: ∆АВС – прямоугольный.
Рис. 5 Доказательство: Пусть СМ ≠ МА и СМ ≠ MB. Для определенности пусть
СМ>МА, После обсуждения нужно
отметить, |
№ 261. Дано:DАВС – равнобедренный, АВ = ВС, АA1, СС1 – высоты. Доказать:АA1 = СС1.
Рис. 3 Доказательство: 1) ÐА1АС = 90° – ÐА1СА || || тогда ÐА1АС = ÐС1СА1. ÐССА = 90° – ÐС1АС 2) DА1АС и DС1СА: АС – общая, ÐА1АС = ÐС1СА (из п. 1), DА1АС = DС1СА (по стороне и двум прилежащим углам), тогда № 268. Дано:DАВС и DА1В1С1, ÐС = ÐС1 = 90°, ÐВ = ÐВ1, АС = А1С1. Доказать:DАВС = DА1В1С1.
Рис. 6 Доказательство: 1) ÐА = 90° – ÐВ || || тогда ÐА = ÐА1, ÐА1 = 90° –ÐВ1 2) Рассмотрим DАВС и DА1В1С1. АС = А1С1 (по
усл.), С = ÐС1 № 269. Дано:DАВС и DА1В1С1, ÐА = ÐА1, ÐВ = ÐВ1, ВН, В1Н1 – высоты, ВН = В1Н1. Доказать:DАВС = DА1В1С1.
Рис. 7 Доказательство: 1) Рассмотрим DАВН и DА1В1Н1. ВН = В1Н1, ÐА = ÐА1, следовательно, DАВН = DА1В1Н1 (по катету и острому углу), тогда АВ = А1В1,
2) Рассмотрим DАВС и DА1В1С1. АВ = А1В1, (из п.
1), ÐА = ÐА1 |
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Перечислите свойства прямоугольных треугольников. – Перечислите признаки равенства прямоугольных треугольников. – Оцените свою работу на уроке. – Составьте синквейн к уроку |
(И) Домашнее задание: изучить п. 36; ответить на вопросы 12–13 на с. 88–89; решить задачи № 262, 264 |
|
Урок 51. Решение задач
|
Цель деятельности учителя |
Создать условия для обучения применению признаков равенства прямоугольных треугольников и их свойств при решении задач, для выработки умения решать задачи; способствовать развитию умения логически мыслить |
|
|
Термины и понятия |
Треугольник, противолежащий угол, катеты, гипотенуза |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, методы для решения задач |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы; понимают и используют математические средства наглядности. Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, в парах, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
|
|
Образовательные |
• Чертежи к задачам. • Задания для самостоятельной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Сформулировать свойства прямоугольных треугольников. 3. Сформулировать признаки равенства прямоугольных треугольников. 4. Устно решить задачи по готовым чертежам. 1) На рисунке 1 ÐВ = ÐС =90°; Ð1 = Ð2. Докажите, что АВ = СD. 2) На рисунке 2 АВ = СD; ВС = АD, ÐАFВ = ÐСЕD = 90°. Докажите, что BF = ED; АF = EC. 3) На рисунке 3 Ð1 = Ð2 = 90°, АВ = DС. Докажите, что ВС = АD. 4) На рисунке 4 АН и А1Н1 – высоты треугольников АВС и А1В1С1; АС = А1С1; Ð1 = Ð2; АН = А1Н1. Докажите, что ∆АВС = ∆А1В1С1.
Рис. 1 Рис. 2 Рис. 3
Рис. 4 |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 263 на доске и в тетрадях. 2. Решить задачу № 267 на доске и в тетрадях. (П) 3. Решить задачи по готовым чертежам. 1) Доказать: ВС^CD.
Рис. 5 2) Найти:ÐАСЕ.
Рис. 6 3) Дано: ВН = 4 см. Найти: АН.
Рис. 7 4) Дано: АВ || CD. Найти: углы ∆CDO.
Рис. 8 5) Дано: О – общая середина АВ и CD, АВ^CD. Доказать: АС = DB.
Рис. 9 6) Доказать: МС – медиана ∆KMN.
Рис. 10 7) Дано: BD – биссектриса ÐАВС. Доказать: DB – биссектриса ÐADC.
Рис. 11 8) Дано: ВМ = 5 см. Найти: ME.
Рис. 12 |
№ 263. Дано:DАВС – равнобедренный, АВ
= АС; Найти:ÐА, ÐВ, ÐС.
Рис. 13 Решение: 1) По свойству смежных углов, 180° – 140° = ÐСМВ1. ÐСМВ1 = 40°, тогда ÐВ1СМ (ВСС1) = 90° – 40° = 50°. 2) ÐА = 90° – ÐВ1СС1 = 90° – 50° = 40°. 3) По свойству углов в треугольнике, ÐВ + ÐС = 180° – ÐА, ÐВ + ÐС = 180° – 40° = 140°. Так как ÐВ = ÐС (АВ = АС), то ÐВ = 70°, ÐС = 70°. Ответ: 40°, 70°, 70°. № 267. Дано:DAВC и DA1В1C1, СС2, ВВ2, С1М1,
В1N1 – высоты; Доказать:DAВC = DA1В1C1.
Рис. 14 Доказательство: 1) Рассмотрим DВ2ВС и DN1В1С1. ВС = В1C1 (по усл.), ВВ2 = В1N1 (по усл.), следовательно, DВ2ВС = DN1В1С1 (по гипотенузе и катету), тогда ÐС = ÐС1 (по определению равных треугольников). 2) Рассмотрим DС2ВС и DМ1В1С1. ВС = В1C1 (по усл.), СС2 = С1М1
(по усл.), следовательно, DС2ВС = DМ1В1С1, 3) Рассмотрим DAВC и DA1В1C1. ВС = В1C1 (по
усл.), |
|
III этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Проверить уровень |
(И) Учащиеся выполняют задания самостоятельной работы (см. Ресурсный материал) |
|
|
IV этап. Итог урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Перечислите свойства прямоугольного треугольника, которые применили при решении задач самостоятельной работы. – Оцените свою работу и работу своего напарника |
(И) Домашнее задание:
повторить п. 30–36, подготовиться |
|
Ресурсный материал
Самостоятельная работа
Вариант I
1. На рисунке 1 АD = DС; ЕD = DF; Ð1 = Ð2 = 90°. Докажите,что треугольник АВС равнобедренный.
2. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.
Вариант II
1. На рисунке 2 Ð1 = Ð2, Ð3 = Ð4 = 90°; ВD = DС. Докажите, что треугольник АВС равнобедренный.
2. Один из острых углов прямоугольного треугольника в два раза меньше другого, а разность гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу и меньший катет.
Вариант III
(для более подготовленных учащихся)
1. Через середину отрезка АВ проведена прямая а. Из точек А и В к прямой а проведены перпендикуляры АС и ВD. Докажите, что АС = ВD.
2. В прямоугольном треугольнике СDЕ с прямым углом Е проведена высота EF. Найдите CF и FD, если СD = 18 см, а ÐDСЕ = 30°.
Вариант IV
(для более подготовленных учащихся)
1. Из точки М биссектрисы неразвернутого угла О проведены перпендикуляры МА и МВ к сторонам этого угла. Докажите, что МА = МВ.
2. В прямоугольном треугольнике АВС с гипотенузой АВ и ÐА = 60° проведена высота СН. Найдите ВН, если АН = 6 см.
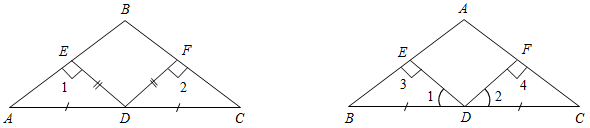
Рис. 1 Рис. 2
Урок52. Решение задач
|
Цель деятельности учителя |
Создать условия для повторения и систематизации ранее изученного материала, выработки навыков решения задач; способствовать развитию логического мышления учащихся |
|
|
Термины и понятия |
Треугольник, противолежащий угол, катеты, гипотенуза |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, результаты, методы для решения задач |
Познавательные: умеют
самостоятельно планировать альтернативные пути достижения целей, осознанно
выбирать наиболее эффективные способы решения учебных и познавательных задач;
понимают Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения, работать в группе. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные |
• Задания для индивидуальной, групповой работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проанализировать ошибки, допущенные в самостоятельной работе |
(Ф/И) 1. Указать ошибки, допущенные в самостоятельной работе. 2. Решить задачи, вызвавшие затруднения у учащихся |
|
|
II этап. Устный опрос |
||
|
Цель деятельности |
Задания для индивидуальной работы |
|
|
Привести в систему знания учащихся по теме «Прямоугольный тре-угольник» |
(Ф) К доске вызываются четверо учащихся, которые работают по карточкам (см. Ресурсный материал). Одновременно учитель проводит беседу с классом, задавая вопросы по теории |
|
|
III этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать |
(Г) Организует деятельность учащихся: решение задач № 299 и 311. Дополнительнаязадача: Через середину стороны АВ
треугольника АВС ВС = 24 см, периметр треугольника АЕС равен Выполнив задание в группах, учащиеся представляют свои решения, обсуждают и записывают в тетрадях |
№ 299. Дано: АВ = АС, АР = PQ = QR = RB = ВC. Найти:ÐА.
Решение: 1) Примем ÐС = ÐВ = х, так как DАВС равнобедренный. Примем ÐСВR = у. Рассмотрим DRQВ: ÐR + ÐQ + ÐВ = 180°. 180° –
х = 4у 2) Рассмотрим DАВС: ÐА + ÐВ + ÐС = 180°. 4у + 4у + у = 180° 9у = 180° у = 20°
Рис. 1 Ответ: ÐА = 20°. № 311. 1) Проведем биссектрисы
углов, образованных при пересечении двух прямых ОА DОDC = DОЕС по гипотенузе (ОС – общая гипотенуза) и острому углу (Ð1 = Ð2), следовательно, CD = СЕ.
Рис. 2 2) Проведем перпендикуляры MN и МР к прямым ОА и ОВ. DОNM = DОРМ по катету и гипотенузе (ОМ – общая гипотенуза, MN = МР, так как по условию точка М равноудалена от сторон ОА и ОВ). Следовательно, ÐNОM = ÐРОМ, то есть луч ОМ – биссектриса ÐАОВ. Из доказанных утверждений следует, что искомое множество точек состоит из двух прямых, содержащих биссектрисы углов, образованных при пересечении данных прямых. Дополнительная задача. Решение: ∆АЕМ = ∆ВЕМ по двум катетам, тогда АЕ = ВЕ. РАЕС = АС + АЕ + СЕ, но так как АЕ = BE,
то РАЕС = АС + (BE + СЕ) = АС +
СВ =
Рис. 3 Ответ: АС = 6 см |
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какие цели были поставлены на уроке? Добились мы их? – Оцените свою работу и работу группы |
(И) Домашнее задание: повторить пункты 15–36; решить задачи № 266, 297; принести циркули и линейки |
|
Ресурсный материал
Карточки для индивидуальной работы
Вариант I
1. Сформулируйте теорему о сумме углов треугольника.
2. Один из углов при основании равнобедренного треугольника равен 65°. Найдите остальные углы треугольника.
3. В треугольнике АВС ÐВ = 110°; биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС.
Вариант II
1. Сформулируйте свойство катета прямоугольного треугольника, лежащего против угла в 30°.
2. В прямоугольном треугольнике АВС ÐС = 90°; ÐВ = 60°, АВ = 15 см. Найдите ВС.
3. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.
Вариант III
1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету.
2. В треугольниках АВС и А1В1С1ÐВ =ÐВ1 = 90°; АВ = А1В1, АС = А1С1. Найдите углы А1 и С1 треугольника А1В1С1, если ÐА = 34°, ÐС = 54°.
3. На сторонах угла А отмечены точки В и С так, что АВ = АС. Через точки В и С проведены прямые, перпендикулярные соответственно сторонам АВ и АС данного угла и пересекающиеся в точке М. Докажите, что МВ = МС.
Вариант IV
1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и острому углу.
2. В треугольниках АВС и А1В1С1углы В и В1прямые, ÐА = ÐА1, АС = А1С1. Найдите стороны В1С1 и А1В1треугольника А1В1С1, если ВС = 17 см, АВ = 12 см.
3. Даны два равных прямоугольных треугольника АВС и А1В1С1, у которых ÐВ =ÐВ1 = 90°; ВН и В1Н1 – высоты. Докажите, что ΔВНС = ∆В1Н1С1.
Урок53. Расстояние от точки до прямой.
Расстояние между параллельными прямыми
|
Цель деятельности учителя |
Создать условия для введения понятия расстояния от точки до прямой и расстояния между параллельными прямыми, для демонстрации применения данных понятий при решении задач |
|
|
Термины и понятия |
Параллельные прямые, расстояние от точки до прямой, перпендикуляр, наклонная |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Знают, какой отрезок называется наклонной, проведенной |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; понимают и используют математические средства наглядности. Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для фронтальной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить правильность
выполнения |
(Ф/И) Двое учеников по желанию выполняют на доске решение домашних задач. № 266. Дано:ÐО, ОА = ОВ, АА1 = ВВ1, АА1ÇВВ1 = С. Доказать: ОС – биссектриса.
Рис. 1 Доказательство: Рассмотрим DОАС и DОВС. ОС – общая, ОА = ОВ (по усл.), следовательно, DОАС = DОВС (по катету и гипотенузе), тогда Ð1 = Ð2 (по определению равных треугольников), тогда ОС – биссектриса. № 297. Дано:DАDС, BÎAD, ВВ1 – биссектриса, BD = ВС, ÐD = ÐВСD. Доказать:ВВ1 || DC.
Рис. 2 Доказательство: 1) ÐD + ÐBСD = 180° – ÐDВC || || ÐD + ÐС = Ð1 + Ð2. Ð1 + Ð2 = 180° – ÐDВC Так как ÐD = ÐС, Ð1 = Ð2, то ÐD = ÐС = Ð1 = Ð2. 2) ÐС и Ð2 – накрест лежащие при ВВ1 и DC и секущей ВС, тогда ВВ1 || DC, что и требовалось доказать |
|
|
II этап. Учебно-познавательная деятельность |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Ввести понятия расстояния от точки до прямой и расстояния между параллельными прямыми |
(Ф/И) 1. Ввести понятие расстояния от точки до прямой. 1) Понятие наклонной – отрезок АВ и ВD. 2) Перпендикуляр АС, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой. 3) Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.
Рис. 3 2. Рассмотреть рисунок 137 из учебника на с. 81. 3. Рассмотреть одно из важнейших свойств параллельных прямых: разобрать доказательство теоремы «Все точки каждой из двух параллельных прямых равноудалены от другой прямой» по рис. 138. 4. Ввести понятие расстояния
между параллельными прямыми: расстояние от произвольной точки одной 5. Рассмотреть утверждение, обратное доказанной теореме. Оно лежит в основе конструкции рейсмуса, применяемого в столярном деле для разметки прямых, параллельных краю бруска (см. рис. 139 учебника) |
|
|
III этап. Закрепление изученного материала |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Научить применять |
(Ф/И) Организует деятельность учащихся. 1. Решить задачи № 271, 275 на доске и в тетрадях. 2. Решить задачу № 278. 3. Решить задачи № 281, 282 по готовым чертежам (устно) |
№ 271. Дано:АВ^а, АС – наклонная, АВ + АС = 17 см, АС – АВ = 1 см. Найти:АВ.
Рис. 4 Решение:
Ответ: 8 см. № 275. Дано:DАВС, АС = СВ, МÎАВ, МЕ^АС, MK^ВС, МЕ = MK. Доказать:СМ ^АВ.
Рис. 5 Доказательство: 1) Рассмотрим DВKM и DАЕМ. KM = ЕМ (по
усл.), ÐВ = ÐА (так как DАВС – 2) Так как М – середина АВ, значит, СМ – медиана равнобедренного треугольника, опущенная на основание, тогда СМ ^АВ. № 278. Дано:АВ || СD, ÐАDС = 30°, АD = 6 см, ВС^АВ. Найти: ВС.
Рис. 6 Решение: 1) Рассмотрим DАА1D: ÐА1 = 90°, ÐD = 30°, так как АА1 лежит против угла 30°, то АА1
= 2) Так как АА1 = ВС, то ВС = 3 см. Ответ: 3 см |
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Что называется перпендикуляром, наклонной, расстоянием от точки до прямой, расстоянием между параллельными прямыми? – Составьте синквейн к уроку |
(И) Домашнее задание: изучить п. 38; ответить на вопросы 14–18 на с. 89 учебника; решить задачи № 272, 277, 283; принести циркули и линейки |
|
Урок54. Построение треугольника по трем элементам
|
Цели деятельности учителя |
Создать условия для рассмотрения задач на построение треугольника по трем элементам |
|
|
Термины и понятия |
Угол, окружность, дуга окружности, отрезок |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: умеют
самостоятельно планировать альтернативные пути достижения целей, осознанно
выбирать наиболее эффективные способы решения учебных и познавательных задач;
понимают Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные |
• Задания для групповой работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать |
(Ф/И) 1. Фронтальный опрос учащихся по изученному ранее материалу. 2. Обсуждение вопросов 14–18 на с. 89. 3. Проверка домашнего задания: двое учащихся на доске решают № 272, 277. № 272. Дано:DАВС, АВ = ВС = АС, АD – биссектриса ÐА, DK^AС, DK = 6 см. Найти:АD.
Рис. 1 Решение: 1) Так как DАВС – равносторонний, то: а) АD^ВС; б) ÐА = ÐВ = ÐС = 60°. 2) Рассмотрим DADK:ÐK = 90°, ÐDAK = 30°, DK = 6 см;
так как DK лежит против угла в 30°, то АD = 2DK; Ответ: 12 см. № 277. Дано:а || b, АВ^а, АВ = 3 см, а || с, MN ^а, MN = 5 см. Найти: расстояние между b и с.
Рис. 2 Решение: 1) Так как а || b (по усл.) а || с (по усл.), следовательно, b || с (свойство параллельных прямых). 2) KF = 5 – 3 = 2 см или KF = 5 + 3 = 8 см.
Ответ: 2 см или 8 см |
|
|
II этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Рассмотреть задачи |
(Г) 1. Напомнить учащимся, что
значит решить задачу на построение с помощью циркуля и линейки; можно
рас-сказать о том, что обычно задачи на построение решаются по схеме,
состоящей из четырех частей: 1) анализ; 2. Продолжить работу в группах. При выполнении задания учащиеся могут общаться друг с другом, обсуждать решение задачи. 1-я группа С помощью циркуля и линейки без делений построить ∆АВС такой, что АВ = PQ, ÐA = ÐМ, ÐВ = ÐN.
Рис. 3 2-я группа С помощью циркуля и линейки без делений построить ∆АВС такой, что АВ = MN, AC = RS, ÐA = ÐQ.
Рис. 4 3-я группа С помощью циркуля и линейки без делений построить ∆АВС такой, что АВ = MN, ВС = PQ, AC = RS.
Рис. 5 Когда группы будут готовы, заслушать решение каждой задачи, обсудить правильность решения. 3. Обсудить общий вопрос для всех групп: – Всегда ли можно построить такой ∆АВС, который удовлетворял бы всем условиям задачи? 4. Решить в тетради задачи (самостоятельно). 1) Построение треугольника по стороне и прилежащим к ней углам. 2) Построение треугольника по двум сторонам и углу между ними. 3) Построение треугольника по трем сторонам |
|
|
III этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 286. 2. Решить задачу № 284 |
№ 286. Дано: Построить:DАВС: АВ = а, ÐА = a, АD = l. Анализ:
Рис. 6 Ход построения: 1) отрезок АВ = а; 2) угол А = a; 3) биссектриса АD = l; 4) соединить В и D прямой; 5) ВDÇ сторону угла А в точке С; 6) DАВС – искомый |
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Что повторили на уроке? Что нового узнали? – Оцените свою работу и работу группы |
(И) Домашнее задание: изучить п. 39 (1 и 2); решить задачи № 274, 285 |
|
Урок55. Решение задач
|
Цели деятельности учителя |
Создать условия для обучения учащихся решению задач на построение с помощью циркуля и линейки |
|
|
Термины и понятия |
Угол, окружность, дуга окружности, отрезок |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Имеют
систематические знания о плоских фигурах и их свойствах, владеют умением
применять систематические знания |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Чертежи к задачам |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Систематизировать полученные знания |
(Ф/И) 1. Ответить на вопросы учащихся по выполнению домашнего задания. 2. Организовать решение
задач № 285, 291 (д) с последующим обсуждением |
№ 285. Построение: 1) Построим прямую l, перпендикулярную прямой b и проходящую через произвольную точку X прямой b. 2) Отложим от точки X на прямой l отрезок XY, равный PQ. 3) Построим прямую с, перпендикулярную прямой l и проходящую через точку Y. 4) Точку пересечения а и с обозначим А. Точка А прямой а удалена от прямой b на расстояние PQ, то есть А – искомая точка. Задача имеет два решения: отрезок XY на прямой l можно отложить в разные стороны от прямой b.
Рис. 1 № 291 (д). Дано: медиана PQ, проведенная к основанию; основание равнобедренного треугольника ST. Построение: Так как медиана, проведенная к основанию равнобедренного треугольника, является его высотой, то ход построения будет следующим: 1) На прямой а отложим отрезок АВ, равный ST. 2) Построим середину отрезка АВ – точку М. 3) Через точку М
построим прямую b, перпендикулярную прямой а, и отложим 4) Соединим точки А и С, В и С отрезками. ∆АВС – искомый. Задача имеет два решения: на прямой b от точки М можно отложить два отрезка, равных PQ.
Рис. 2 |
|
II этап. Учебно-познавательная деятельность |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Изучить новый мате- |
(Ф/И) 1. Разобрать решение задачи № 3 на доске и в тетрадях (с. 84–85). 2. Построить треугольник по трем сторонам (рис. 141 и решение задачи на с. 85 учебника). Провести исследование, всегда ли задача № 3 имеет решение |
|
|
III этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать навыки в решении задач |
(Ф/И) Организует
деятельность учащихся: решение |
№ 289. Дано: ПостроитьDАВС: АВ = PQ, ÐА = hk, ÐВ = Анализ:
Ход построения: 1) Отрезок АВ = PQ; 2) ÐА =hk; 3) ÐВ = 4) стороны ÐА и ÐВ пересекаются в точке С; 5) DАВС – искомый.
№ 290. а) Дано: ПостроитьDАВС: ÐС = 90°, АС = а, СВ = b. Анализ:
Ход построения: 1) Построить прямой угол С; 2) на одной стороне отложить отрезок АС = а, а на другой – СВ = b; 3) соединить отрезком А и В; 4) DАВС – искомый. б) Дано: ПостроитьDАВС: ÐС = 90°, ÐА = a, АС = а. Анализ:
Ход построения: 1) Построить прямой угол С; 2) отложить на стороне угла АС = а; 3) построить ÐА = a; 4) стороны ÐА и ÐС пересекаются в точке В; 5) DАВС – искомый. № 292. Дано: а) ПостроитьDАВС: АВ = P1Q1, ВС = P2Q2, АС = 2P3Q3. Анализ:
Ход построения: 1) Отрезок АВ = P1Q1; 2) окружность с центром А и R = P2Q2; 3) окружность с центром В и R = 2P3Q3; 4) эти две окружности пересекаются в точке С; 5) DАВС – искомый. б) ПостроитьDАВС: АВ = 2P1Q1,
ВС = P2Q2, АС = Анализ:
Ход построения: 1) ВС = P2Q2; 2) окружность с центром В и R = 2P1Q1; 3) окружность с центром С
и R = 4) окружности пересекаются в точке А; 5) DАВС – искомый. Указание: нужно помнить, что сумма длин двух сторон треугольника должна быть больше длины третьей стороны |
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Оцените свою работу на уроке. – Закончите фразы: • Я познакомился с... • Было непросто... • Я добился... • У меня получилось... • Хотелось бы... • Мне запомнилось... • Я попробую... |
(И) Домашнее задание: пункты
38–39; вопросы 14–20 на с. 89; решить задачи |
|
Урок56. Решение задач
|
Цель деятельности учителя |
Создать условия для обучения учащихся решению задач на построение с помощью циркуля и линейки |
|
|
Термины и понятия |
Угол, окружность, дуга окружности, отрезок, искомый треугольник |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Усваивают систематические
знания о плоских фигурах и их свойствах, владеют умениями применять
систематические знания о них для геометрических |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: осуществляют контроль по результату и по способу действия на уровне произвольного внимания и вносят необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для фронтальной работы. • Задания для самостоятельной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать |
(Ф/И) 1. Проверить выполнение домашней работы. 2. Решить задачи. 1) В треугольнике ABCÐС = 30°, АС = 10 см, ВС = 8 см. Через вершину А проведена прямая а, параллельная ВС. Найдите: а) расстояние от точки В до прямой АС; б) расстояние между прямыми а и ВС. 2) Постройте равносторонний треугольник, у которого сторона в два раза меньше данного отрезка |
|
|
II этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Проверить уровень владения умением решать задачи на построение |
(И) Работа выполняется на листках и в конце урока сдается на проверку учителю. Вариант I 1. Постройте прямоугольный треугольник по катету и прилежащему острому углу. 2. Даны отрезки PQ и P1Q1 и угол hk. Постройте треугольник СDЕ так, чтобы СЕ = PQ, ÐС = Ðhk, СF = P1Q1, где СF – высота треугольника. Вариант II 1. Постройте равнобедренный треугольник по основанию и медиане, проведенной к основанию. 2. Даны отрезки PQ, P1Q1
и P2Q2. Постройте треугольник ЕKF так,
чтобы ЕF = PQ, KF = P1Q1 и FD =
P2Q2, |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Почему было трудно? – Что открыли, узнали на уроке? – Оправдались ли ваши ожидания от урока? – Что вы взяли с сегодняшнего урока? |
(И) Домашнее задание: решить задачи № 294, 295 |
|
Урок57. Решение задач
|
Цели деятельности учителя |
Создать условия для обучения учащихся решению задач на построение с помощью циркуля и линейки, для подготовки к контрольной работе |
|
|
Термины и понятия |
Угол, окружность, дуга окружности, отрезок, искомый треугольник |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Закрепляют систематические
знания о плоских фигурах и их свойствах; владеют умениями применять
систематические знания о них для геометрических |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: осуществляют контроль по результату и по способу действия на уровне произвольного внимания и вносят необходимые коррективы; умеют контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, в группе. Личностные: осознают важность и необходимость изучения предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные |
• Задание для фронтальной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать |
(Ф/И) 1. Проверить выполнение домашнего задания. Для этого вызвать к доске двоих учащихся. № 294. Дано: ПостроитьDАВС: АВ = b, АС = а, CD = c, CD^AB. Анализ:
Ход построения: 1) Прямой угол D; 2) на одной стороне отложить отрезок DC = h; 3) окружность с центром в точке C и R = а; 4) окружность пересечет другую сторону прямого ÐD в точке А; 5) отложить АВ = b; 6) DАВС – искомый.
№ 295. Дано: Построить DАВС. Анализ:
Ход построения: 1) Отрезок АВ = а; 2) середина АВ – точка D; 3) окружность с центром в точке D и R = т и окружность с центром в точке А и R1 = b; 4) окружности пересекаются в точке С; 5) соединить отрезком точки В и С; 6) DАВС – искомый. 2. Сообщить результаты самостоятельной работы |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать |
(Г) Организует деятельность 1. Решить задачи по группам:
(Ф/И) 2. Построить прямоугольный треугольник по гипотенузе и внешнему углу при вершине острого угла. Решение: Начертим данные отрезок PQ
Рис. 1 Построение: 1) Проведем прямую, отметим 2) Отложим от луча ВD, являющегося продолжением луча ВС, угол DВМ, равный углу hk. 3) Построим прямую,
проходящую через точку С и перпендикулярную к прямой ВМ, и
обозначим
Рис. 2 Доказательство (устно): По построению треугольник АВС
– Указание:задача имеет решение только в том случае, когда данный угол hkтупой. Желательно, чтобы учащиеся сами обосновали справедливость этого утверждения |
№ 301. Дано: АН^а, АМ1, АМ2 – наклонные. а) Доказать:АМ1 = АМ2, если НМ1 = НМ2.
Рис. 3 Рассмотрим DАНМ1 и DАНМ2: АН – общая, НМ1
= НМ2 (по усл.), DАНМ1 = б) Доказать: АМ1<АМ2, если НМ1<НМ2.
Рис. 4 1) В DАНМ1: ÐН = 90°, значит, Ð1 – острый. 2) ВDАНМ2: ÐН = 90°, значит, Ð2 – острый. 3) В DАМ1М2: Ð2 – острый, Ð3 – тупой (как смежный с острым), значит АМ2>АМ1, что и требовалось доказать. № 302. Дано: АН^а, АМ1, АМ2 – наклонные. а) Доказать:НМ1 = НМ2, если АМ1 = АМ2.
Рис. 5 Рассмотрим DАНМ1 и DАНМ2: АН – общая, АМ1
= АМ2 (по усл.), DАНМ1 = б) Доказать:НМ1<НМ2, если АМ1<АМ2.
Рис. 6 1) Примем НМ1 не <НМ2, то есть НМ1>НМ2 или НМ1 = НМ2. 2) Если НМ1 = НМ2, то получим результат аналогично 301 (а), что противоречит условию АМ1<АМ2, значит, предположение НМ1 = НМ2 неверно. 3) Если НМ1>НМ2, то, по 301 (б), получим АМ1>АМ2, значит, предположение НМ1>НМ2 неверно. Вывод: НМ1<НМ2. № 308. Дано:DАВС – равнобедренный, АС = 37 см – основание, внешний угол при вершине В равен 60°. Найти: расстояние от вершины С до прямой АВ.
Рис. 7 Решение: 1) DАВС – равнобедренный; по задаче
232, 2ÐА = 60°, следовательно, 2) DСНА – прямоугольный (по
условию), ÐА = 30°, следовательно, № 315. Построить при помощи циркуля и линейки угол, равный: а) 30°; б) 60°; в) 15°; г) 120°; д) 150°; е) 135°; ж) 75°; и) 105.
Рис. 8 а) Ход построения: 1) Возьмем произвольную прямую а и произвольную точку АÎа; 2) строим прямую b так, чтобы АÎb и а^b (по задаче о построении перпендикулярных прямых); 3) находим точку В, чтобы ВÎb и АВ – произвольной длины; 4) строим окружность w с центром в точке В и радиусом, равным 2АВ; 5) окружность w пересекает прямую а в точке О; 6) DАВС – искомый. Доказательство: DАОВ – прямоугольный (по построению) и АВ = б) Угол в 60° построен в п. а) одновременно с углом в 30° (это ÐОВА). в) Построенный в п. а) угол
в 30° следует разделить пополам (по задаче г) Поскольку 120° = 180° – 60°, этот угол построен в п. а) – это угол, смежный ÐАВО. д) Поскольку 150° = 180° – 30°, этот угол построен в п. а) – это угол, смежный ÐАОВ. е) Поскольку 135° = 90° + 45°, следует построить две перпендикулярных прямых и один из полученных прямых углов разделить пополам (по задаче о построении биссектрисы угла). ж) Поскольку 165° = 180° –
15°, это угол, смежный построенному в п. в). и) Поскольку 105° = 90° + 15°, это другой из углов, полученных в п. ж). № 316. Дано:P1Q1 – сторона, P2Q2 – высота к P1Q1, P3Q3 – медиана. Построить:DАВС (СН = P2Q2, АМ = P3Q3, АВ = P1Q1). Ход построения: Строим две параллельные прямые, расположенные друг от друга на расстоянии, равном данной высоте треугольника. На одной из прямых отмечаем точку А и откладываем отрезок АВ, равный данной стороне треугольника. Строим окружность с центром А и радиусом, вдвое большим данной медианы треугольника. Строим середину М отрезка AD, где D – точка пересечения окружности и второй прямой, и проводим прямую ВМ до пересечения со второй из параллельных прямых в точке С. DАВС – искомый
Рис. 11 |
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Обычно мы заканчиваем
урок, оценивая свою работу |
(И) Домашнее задание: решить задачи № 314, 317; подготовиться к контрольной работе |
|
Урок58. Решение задач
|
Цели деятельности учителя |
Создать условия для обучения учащихся решению задач на построение с использованием циркуля и линейки, для подготовки к контрольной работе |
|
|
Термины и понятия |
Угол, окружность, дуга окружности, отрезок, искомый треугольник |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют систематическими
знаниями о плоских фигурах и их свойствах, умениями применять систематические
знания о них для решения геометрических |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, в группе. Личностные: осознают важность и необходимость геометрических знаний для жизни человека |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
|
|
Образовательные |
• Задания для парной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверитьвыполнениедомашнего задания |
(Ф/И) К доске вызывается учащийся для проверки решения № 317. № 317. Дано:DАВС. Построить: отрезок DE, такой, чтобы DE || AC, DÎAB, EÎBC, DE = AD + CE.
Рис. 1 Ход построения: 1) Строим прямую а – биссектрису ÐА (по задаче о построении биссектрисы угла); 2) строим прямую с – биссектрису ÐС (по задаче о построении биссектрисы угла); 3) аÇс в точке О; 4) строим прямую b, чтобы ОÎb и b^АС (по задаче 153); 5) строим прямую d, чтобы d^b и ОÎd (по задаче о построении перпендикулярных прямых); 6) dÇАВ в точке D, dÇВС в точке Е; 7) DE – искомый. Доказательство: В DАВСа – биссектриса ÐА, с – биссектриса ÐС (по построению), d^b, b^АС, следовательно, d ||
АС, |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
(П) Решение задач на готовых чертежах на повторение свойств прямоугольных треугольников, признаков равенства прямоугольных треугольников, понятий расстояния между параллельными прямыми и расстояния от точки до прямой (самостоятельно с последующей проверкой; в тетрадях записать только ответы; рисунки к задачам и их условия подготовить заранее, раздать на каждую парту). 1) Найти:ÐВЕА, СЕ, АС. 2) Найти: AD, AB. 3) Найти: АВ, ÐBCM, ÐAMC.
Рис. 2 Рис. 3 Рис. 4 4) Найти:ÐA, AB. 5) Найти: АС. 6) Найти: DC, AC.
Рис. 5 Рис. 6 Рис. 7 7) Дано: а || b. Найти: расстояние между прямыми а и b.
Рис. 8 8) Найти: расстояние от точки А до прямой а. 9) Найти: расстояние от точки K до прямой а.
Рис. 9 Рис. 10 10) Укажите равные треугольники. 11) Укажите равные треугольники. Найти:ÐBCD. Найти:ÐEAD, ÐAED.
Рис. 11 Рис. 12 12) Укажите равные треугольники. 13) Дано: CL – биссектриса. Найти: АВ. Найти:ÐA, ÐВ.
Рис. 13 Рис. 14 14) Дано: СМ – медиана. 15) Дано:Ð1 : Ð2 = 2 : 3. Найти:ÐA, ÐB. Найти:ÐA, ÐC.
Рис. 15 Рис. 16 Ответы: 1) ÐВЕА = 120°, СЕ = 3 см, АС = 9 см; 2) AD = 4 см, AB = 8 см; 3) АВ = 12 см, ÐВСМ = 40°, ÐAMC = 80°; 4) ÐA = 60°, АВ = 6 см; 5) АС = 8,5 см; 6) DC = 4 см, АС = 12 см; 7) 10 см; 8) 9 см; 9) 2 см; 10) ∆АВС = ∆ADC, ÐBCD = 130°; 11) ∆ABD = ∆DCA, ÐAED = 110°, ÐEAD = 35°; 12) ∆АВМ = ∆СВМ, АВ = 6 см; 13) ÐA = 25°, ÐB = 65°; 14) ÐA = 35°, ÐB = 55°; 15) ÐA = 72°, ÐB = 18° |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Оцените себя: насколько вы готовы к контрольной работе? – Какие возникли затруднения? |
(И) Домашнее задание: решить те задачи, которые не успели в классе |
|
Урок 59. Контрольная работа № 5
|
Цель деятельности учителя |
Создать условия для проверки
знаний, умений и навыков учащихся по усвоению и применению изученного |
|
|
Термины и понятия |
Треугольник, неравенство треугольника, соотношения между сторонами и углами треугольника |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость изучения предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для контрольной работы |
|
|
I этап. Выполнение контрольной работы |
||
|
Цель деятельности |
Задания для контрольной работы |
|
|
Проверить знания, умения и навыки по изученному материалу |
(И) Вариант I 1. Дано:ÐBAD = ÐBCD = 90°, ÐADB = 15°, ÐBDC = 75°. Доказать: AD || ВС.
Рис. 1 2. В треугольнике ABCÐC = 60°, ÐВ = 90°. Высота ВВ1 равна 2 см. Найдите АВ. 3. Постройте равнобедренный треугольник по основанию и высоте, проведенной к нему из вершины треугольника. 4*. С помощью циркуля и линейки постройте угол, равный 150°. Вариант II 1. Дано:ÐAOD = 90°, ÐOAD = 70°, ÐОСВ = 20°. Доказать: AD || ВС.
Рис. 2 2. В треугольнике ABCÐC = 90°, СС1 – высота, СС1 = 5 см, ВС = 10 см. Найдите ÐCAB. 3. Постройте равнобедренный треугольник по основанию и медиане, проведенной к нему из вершины треугольника. 4*. С помощью циркуля и линейки постройте угол, равный 120° |
|
|
II этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
– Что выполняли на уроке? – Какие задания вызвали затруднения? Почему? – Как оцениваете свою работу на уроке? |
(И) Домашнее задание: повторить пункты 1–14 на с. 5–29 учебника |
|
Урок60. Анализ ошибок контрольной работы
|
Цель деятельности учителя |
Совершенствовать навыки решения задач; развивать навыки самопроверки выполненных работ, умение находить свои ошибки; создать условия для устранения пробелов в знаниях учащихся |
|
|
Термины и понятия |
Треугольник, неравенство треугольника, соотношения между сторонами и углами треугольника |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость геометрических знаний в жизни человека |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для индивидуальной работы |
|
|
I этап. Общий анализ контрольной работы |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Устранение пробелов |
(Ф/И) 1. Общее впечатление о выполненной работе. 2. Решение (или обсуждение) задач, с которыми не справились большинство учащихся. 3. Демонстрация лучших работ |
|
|
II этап. Выполнение работы над ошибками |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
(Ф/И) 1. Найти свои ошибки в решениях задач и устранить их с помощью
учителя или ученика, справившегося 2. Решить задачи другого варианта. Если ученик выполнил
контрольную работу – решает дополнительные Дополнительные задачи. Задача 1. Через точку K, взятую на стороне АВ треугольника АВС, проведена прямая, перпендикулярная АВ и пересекающая сторону АС в точке D. Известно, что ÐKDB = ÐKDA, АС = 30 см, ВС = 15 см. Найдите периметр треугольника ВDС.
Рис. 1 Решение: ∆ADK = ∆BDK по катету и прилежащему к нему острому углу, следовательно, AD = BD. PBDC = BD + DC + CB = (AD + DС) + СВ = АС + СВ = 30 см + 15 см = 45 см. Ответ: РВDС = 45 cм. Задача 2. Докажите, что биссектриса угла А треугольника ABC проходит через точку пересечения прямых, содержащих биссектрисы внешних углов при вершинах В и С.
Рис. 2 Доказательство: ВО и СО – биссектрисы ÐМВС и ÐРСВ соответственно. Докажем, что АО – биссектриса ÐВАС. Проведем ОМ^АВ, ОK^ВС, ОР^АС, тогда ∆ВОМ = ∆ВОK, ∆СОK = ∆СОР по гипотенузе и острому углу. Следовательно, ОМ = ОK= ОР. ∆АОМ = ∆АОР по катету и гипотенузе, отсюда ∆МАО = ∆РАО, то есть АО – биссектриса ÐВАС. Задача 3. Дано: точки М и Т равноудалены от прямой РK, ÐKMT = ÐРТМ. Доказать: ∆РМK = ∆РKТ.
Рис. 3 Доказательство: ÐKMT = ÐРТМ, тогда ÐЕМK = ÐSTP, значит, ∆ЕМK = ∆STP по катету и прилежащему к нему острому углу, следовательно, ÐМKP = ÐТРK, а МK = ТР. ∆РМK= ∆KТР по двум сторонам и углу между ними |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какие темы вызвали у вас наибольшее затруднение? |
(И) Домашнее задание: повторить главу I, вопросы 1–21 |
|
Урок 61. Повторение. Начальные геометрические сведения
|
Цели деятельности учителя |
Создать условия для приведения в систему знаний, умений, навыков учащихся по теме; совершенствовать навыки решения задач |
|
|
Термины и понятия |
Признаки равенства треугольников, боковая сторона, основание, медиана, биссектриса, высота, углы при основании |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют познавательный интерес к изучению предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для игры |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Привести в систему знания по данной теме |
(Ф/И) 1. Класс разделить на 2 группы – теоретиков и практиков;теоретики выбирают теоретические вопросы и направляются к доске, готовят рисунки для ответов;практики выбирают задачу, решают на подписанном листке и передают для проверки жюри (учителю). 2. По мере освобождения места у доски группы меняются: практики становятся теоретиками, а теоретики – практиками. 3. Подведение итогов |
|
|
II этап. Игра |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Привести в систему
теоретические знания учащихся и совершенствовать навыки решения |
Учитель предлагает провести игру: ответить на вопросы и решить задачи (см. Ресурсный материал) |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) Учитель подводит итог игры. Чтобы знания были впрок Надо повторить урок. – Каким сегодня был урок (закрепление или открытие) и почему? – Что нам помогало на уроке? – Оцените свою работу на уроке |
(И)Домашнее задание: написать сочинение на тему «Зачем нужно знать геометрию?» |
|
Ресурсный материал
Игра
Теоретические вопросы.
1. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.
2. Что такое градусная мера угла?
3. Какой угол называется развернутым?
4. Луч ОС делит угол АОВ на два угла. Как найти градусную меру угла АОВ, если известны градусные меры углов АОС и СОВ?
5. Сколько прямых можно провести через две прямые точки?
6. Объясните, как сравнить два угла.
7. Какие фигуры называются равными?
8. Какой угол называется острым? прямым? тупым?
9. Сколько общих точек могут иметь две прямые?
10. Какой луч называется биссектрисой угла?
11. Объясните, как сравнить два отрезка.
12. Какие углы называются смежными? Чему равна сумма смежных углов?
13. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы?
14. Какие приборы применяют для построения прямых углов на местности?
15. Какая точка называется серединой отрезка?
16. Какие прямые называются перпендикулярными?
17. Объясните, что такое луч. Как обозначаются лучи?
18. Какими инструментами пользуются для измерения расстояний?
Задачи.
1. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 220°.
2. На прямой b отмечены точки С, D и Е, причем СD = 6 см, DЕ = 8 см. Какой может быть длина отрезка СЕ?
3. Три точки В, D и С лежат на одной прямой. Известно, что ВD = 17 см, DС = 25 см. Какой может быть длина отрезка ВС?
4. Один из смежных углов на 28° меньше другого. Найдите оба смежных угла.
5. Начертите угол 132° и проведите биссектрису смежного с ним угла.
6. Точка М – середина отрезка АВ, МВ = 4,3 дм. Найдите длину отрезка АВ.
7. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 300°.
8. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD.
9. Три точки М, N и K лежат на одной прямой. Известно, что МN = 15 см, NK = 18 см. Каким может быть расстояние МK?
10. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD.
11. Один из смежных углов в 11 раз больше другого. Найдите оба смежных угла.
12. Один из смежных углов в 8 раз больше другого. Найдите оба смежных угла.
13. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла.
14. Точка М – середина отрезка АВ, МВ = 2,5 см. Найдите длину отрезка АВ.
15. Один из смежных углов равен 52°. Найдите другой угол.
16. Один из вертикальных углов, образованный при пересечении двух прямых, равен 35°. Найдите другие неразвернутые углы.
17. Точки А, В, М лежат на одной прямой. Длина отрезка АВ = 7,3 см, АМ = 3 см. Какой может быть длина отрезка МВ?
18. ОС – биссектриса угла АОВ. Известно, что угол АОС равен 43°. Найдите градусную меру угла АОВ.
Урок62. Повторение. Признаки равенства треугольников.
Равнобедренный треугольник
|
Цели деятельности учителя |
Создать условия для
систематизации знаний, умений, навыков учащихся по данной теме;
совершенствовать |
|
|
Термины и понятия |
Признаки равенства треугольников, боковая сторона, основание, медиана, биссектриса, высота, углы при основании |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Применяют изученные понятия, результаты, методы для решения задач практического характера |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы, контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: осознают важность и необходимость изучения предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
|
|
Образовательные |
• Задания для фронтальной (парной) работы. • Тест |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Устранить пробелы |
(Ф/И) Заслушать сочинения учащихся |
|
|
II этап. Тест |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать |
(И) Учащиеся выполняют тестовые задания (см. Ресурсный материал) |
|
|
III этап. Решение задач по готовым чертежам |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
(Ф/И/П) Записать короткое решение к задачам по готовым чертежам. 1) Доказать: DB – биссектриса ÐADC. 2) Доказать: О – середина АВ.
Рис. 1 Рис. 2 3) Дано: С – середина АЕ, ВС + CD = 10 см. 4) Доказать: ВС = DC. Найти: ВС.
Рис. 3 Рис. 4 5) Доказать: ВЕ = АС, ED = DC. 6) Найти:ÐBFC.
Рис. 5 Рис. 6 7) Найти:ÐAFD. 8) Найти:ÐBAC. 9) Найти: АВ.
Рис. 7 Рис. 8 Рис. 9 |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
§ – Уточните алгоритм исправления ошибок. § – Назовите способы действий, вызвавшие затруднение. § – Оцените собственную деятельность на уроке |
(И) Домашнее задание: повторить главу III, вопросы 1–15; решить оставшиеся задачи. Дополнительные задачи: № 328–332 на выбор учащихся |
|
Ресурсный материал
Тест
1. Для доказательства равенства ∆АВС и ∆DEF (рис. 1) достаточно доказать, что:
а) AB = DF; б) AC = DE; в) AB = DE.
2. Для доказательства равенства ∆АВС и ∆EDF (рис. 2) достаточно доказать, что:
a) ÐA = ÐD; б)ÐB = ÐD; в)ÐA = ÐE.
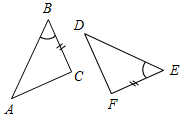
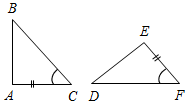
Рис. 1 Рис. 2
3. Из равенства ∆АВС и ∆FDE (рис. 3) следует, что:
a) AB = FD; б) AC = DF; в) AB = EF.
4. Из равенства ∆АВС и ∆DEF (рис. 4) следует, что:
a) ÐB = ÐD; б) ÐA = ÐE; в) ÐC = ÐF.
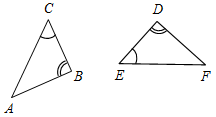
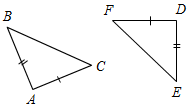
Рис. 3 Рис. 4
5. В ∆ABC все стороны равны, и в ∆DEF все стороны равны. Чтобы доказать равенство ∆АВС и ∆DEF, достаточно доказать, что:
a) ÐВ = ÐD; б) AB = DE; в) РАВС = PDEF.
6. «Медиана в равнобедренном треугольнике является биссектрисой и высотой». Это утверждение:
а) всегда верно; б) всегда неверно; в) может быть верно.
7. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом; б) равнобедренном; в) равностороннем.
8. Если в треугольнике два угла равны, то этот треугольник:
а) равнобедренный; б) равносторонний; в) прямоугольный.
9. Если треугольник равносторонний, то:
а) он равнобедренный; б) все его углы равны; в) любая его биссектриса является его медианой и высотой.
Ответы: 1 – в; 2 – в; 3 – а; 4 – в; 5 – б, в; 6 – в; 7 – б; 8 – а; 9 – а, б, в.
Урок63. Повторение. Признаки равенства треугольников.
Равнобедренный треугольник
|
Цели деятельности учителя |
Создать условия для систематизации знаний, умений, навыков учащихся по данной теме; совершенствовать навыки решения задач по теме «Признаки равенства треугольников. Равнобедренный треугольник» |
|
|
Термины и понятия |
Признаки равенства треугольников, боковая сторона, основание, медиана, биссектриса, высота, углы при основании |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, результаты, методы для решения задач практического характера |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в группе, в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют познавательный интерес к изучению предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные |
• Задания для теста. • Задания для групповой и домашней работы |
|
|
I этап. Тестовые задания |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Повторить теоретические сведения |
(И) Блицтест (10 мин). Тест сдается на проверку учителю. Задание № 1 (оценивается в 4 балла). Отрезки MN и KB пересекаются в точке А. Точка А является серединой этих отрезков. Докажите, что треугольники MKA и NBA равны (рис. 1).
Рис. 1 Задание № 2 (оценивается в 6 баллов). Луч АВ – биссектриса угла АОЕ, перпендикулярен отрезку ОЕ. Найдите длину отрезка АО, если АЕ = 5 см |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
(Г) Класс разбивается на 4 группы. Учащиеся 15 минут работают в группах, затем представляют свои решения, обсуждают задачи. 1) На рисунке 2 ВЕ и СF – высоты ∆АВС. При помощи только линейки постройте высоту АХ этого треугольника. Найдите длину ВС, если АХ = ВЕ, СХ = СЕ, АС = 17 дм.
Рис. 2 2) На рисунке 3 ∆АВС – равнобедренный, L – середина АС, АМ = СK. Доказать, что ML = LK.
Рис. 3 3) На рисунке 4 ÐНKN = ÐMNK, KО = ОN. Доказать, что ÐKHN = ÐKMN.
Рис. 4 |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какие свойства равнобедренного треугольника повторили? – Оцените свою работу и работу группы |
(И) Домашнее задание: решить тест. Каждое из заданий № 1, 2 оценивается в 4 балла. 1. Укажите номера верных утверждений. 1) Высота треугольника всегда лежит внутри треугольника. 2) Медиана – это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. 3) В равнобедренном треугольнике медиана совпадает с биссектрисой, проведенной из той же вершины. 4) В равностороннем треугольнике все углы равны. 2. Докажите, что биссектриса равностороннего треугольника разбивает его на два равных треугольника |
|
Урок64. Повторение. Параллельные прямые
|
Цели деятельности учителя |
Создать условия для приведения в систему знаний, умений, навыков по теме «Параллельные прямые»; совершенствовать навыки решения задач |
|
|
Термины и понятия |
Параллельные прямые, аксиома параллельности, накрест лежащие углы, соответственные углы, односторонние углы |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы, контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: осознают важность и необходимость изучения предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для теста. • Задания для фронтальной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Задания для математического диктанта |
|
|
Привести в систему |
(Ф/И) 1. Проверка домашнего задания. Обсуждение вопросов учащихся. (И) 2. Тест на проверку
теоретических знаний (самостоятельное выполнение с последующим
обсуждением) |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
(Ф/И) Решение задач (устно). 1. Найти: параллельные прямые. 2. Найти: параллельны ли прямые а и b?
Рис. 1 Рис. 2 Ответ: а || с. Ответ: да. 3. Найти: параллельны ли прямые а и b? 4. Дано: а || b. Найти:Ð1, Ð2.
Рис. 3 Рис. 4 Ответ: нет. Ответ: Ð1 = 100°, Ð2 = 80°. 5. Дано: а || b. 6. Найти:Ð1, Ð2. Найти:Ð1, Ð2.
Рис. 5 Рис. 6 Ответ: Ð1 = 50°, Ð2 = 130°. Ответ: Ð1 = 130°, Ð2 = 50°. 7. Найти:Ð1, Ð2. 8. Найти:Ð1.
Рис. 7 Рис. 8 Ответ: Ð1 = 70°, Ð2 = 70°. Ответ: Ð1 = 76°. 9. Найти:Ð1. 10. Найти:Ð3.
Рис. 9 Рис. 10 Ответ: Ð1 = 34°. Ответ: Ð3 = 80°. 11. Найти:ÐМОЕ. 12. Найти: параллельны ли АВ и СD?
Рис. 11 Рис. 12 Ответ: ÐМОЕ = 90°. Ответ: да. 13. Дано: а || b, DE – секущая, DE = 3,9 см. 14. Дано:Ð2 – Ð1 = 44°. Найти: MN. Найти:Ð1, Ð2.
Рис. 13 Рис. 14 Ответ: MN = 7,8 см. Ответ: Ð1 = 68°, Ð2 = 112°. 15. Найти:ÐABC. 16. Найти:ÐEMN.
Рис. 15 Рис. 16 Ответ: ÐABC = 58°. Ответ: ÐEMN = 106°. 17. Дано:ÐABD : ÐDBK = 1 : 2, DB || EC. 18. Найти:ÐACK. Найти:ÐECP.
Рис. 17 Рис. 18 Ответ: ÐECP = 150°. Ответ: ÐACK = 84° |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Сформулируйте аксиому параллельности. – Сформулируйте признаки параллельности прямых. – Оцените свою работу на уроке |
(И) Домашнее задание: повторить главу IV (§ 1, 2, 3), вопросы 1–18 (без доказательства); записать полное решение задач 1–18 (для выполнения этого задания можно класс разбить на варианты) |
|
Ресурсный материал
Тест
1. Если a^с, b^с, то:
а) а || b; б) a^b; в) ответы а) и б) неверны.
2. Если а || с, b || с, то:
a) a^b; б) а || b; в) ответы а) и б) неверны.
3. Рис. 1. Если а || b, с – секущая, то:
a) Ð2 + Ð3 = 180°; б) Ð5 = Ð2; в) Ð1 + Ð3 = 180°.
4. Рис. 2. Для того чтобы прямые а и b были параллельными, нужно, чтобы:
a) Ð1 + Ð4 = 180°; б) Ð1 = Ð2; в) Ð3 = Ð2.
5. Рис. 3. PR || QD, так как:
a) Ð3 = Ð7; б) Ð8 = Ð4; в) Ð2 = Ð6.
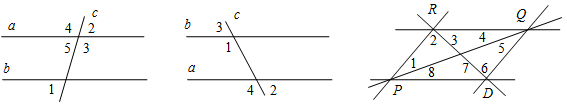
Рис. 1 Рис. 2 Рис. 3
6. Один из углов при пересечении двух параллельных прямых третьей равен 52°. Остальные углы равны:
а) 52° и 132°; б) 52° и 128°; в) 52°.
7. Известно, что M, N, PÎх, MN || x, NP || x. Тогда:
а) MN || NP; б) MN совпадает с NP; в) MNÇNP.
8. Прямая АВ пересекает параллельные прямые РK и MN (AÎРK, ВÎMN). Сумма углов РАВ и МВА равна 116°. Какие из следующих высказываний верны?
а) Точки K и М лежат в одной полуплоскости относительно прямой АВ.
б) Точки Р и N лежат в разных полуплоскостях относительно прямой АВ.
в) Сумма углов РАВ и NBA равна 180°.
9. Прямая MN является секущей для прямых АВ и CD (МÎАВ, NÎCD). Угол AMN равен 78°. При каком значении угла CNM прямые АВ и CD могут быть параллельны?
а) 102°; б) 12°; в) 78°; г) 78° и 102°.
Ответы: 1 – а; 2 – б; 3 – в; 4 – в; 5 – в; 6 – б; 7 – б; 8 – а, в; 9 – г.
Урок65. Повторение. Параллельные прямые
|
Цели деятельности |
Создать условия для приведения в систему знаний, умений, навыков по теме «Параллельные прямые»; совершенствовать навыки решения задач |
|
|
Термины и понятия |
Параллельные прямые, аксиома параллельности, накрест лежащие углы, соответственные углы, односторонние углы |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют познавательный интерес к изучению предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
|
|
Образовательные |
• Задания для проверочной работы. • Задания для теста. • Задания для домашней работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Задания для проверочной работы |
|
|
Привести в систему |
(И) Проверочная работа на 5–7 минут с взаимопроверкой. Каждое из заданий № 1, 2 оценивается в 4 балла. 1. Укажите номера верных утверждений. 1) Если прямая а параллельна прямой с, а прямая с параллельна прямой b, то прямые а и b параллельны. 2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 3) Если точка не лежит на
данной прямой, то через нее не всегда можно провести прямую, параллельную 4) Если прямая а
перпендикулярна прямой с, а прямая с перпендикулярна прямой b,
то прямые а и bпересе- 2. По данным рисунка докажите, что прямые с и а параллельны.
|
|
|
II этап. Тест |
||
|
Цель деятельности |
Тестовые задания |
|
|
Совершенствовать |
(П) Решают тест (см. Ресурсный материал),затем проверяют по готовым ответам |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Сформулируйте признаки параллельности прямых. – Сформулируйте свойства параллельных прямых. – Оцените свою работу в паре |
(И)Домашнее задание. Задание № 1 (оценивается в 4 балла). 1. Прямые а и b параллельны, с – секущая. По данным рисунка найдите все неизвестные углы.
Задание № 2 (оценивается в 6 баллов). По данным рисунка найдите х.
|
|
Ресурсный материал
Тест
Часть 1
А1. На рисунке секущей является прямая…
а) b; б) a; в) c; г) b или с.
А2. Для угла 4 односторонним будет угол…
а) 1; б) 8; в) 5; г) 3.
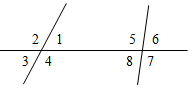
А3. На рисунке углы 1 и 2 являются…
а) односторонними; в) накрест лежащими;
б) смежными; г) соответственными.
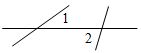
А4. Дан тупоугольный треугольник АВС с тупым углом В. Через вершину В прямых, параллельных АС, провести…
а) можно бесконечное множество; в) можно две;
б) можно одну; г) нельзя ни одной.
А5. На рисунке Ð1 = 112°. Прямые т и п будут параллельными, если Ð2 равен…
а) 68°; б) 112°; в) 58°; г) 68° или 112°.
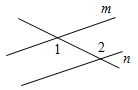
А6. Прямые будут параллельными на рисунке:
а) 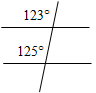 в)
в) 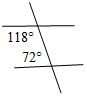
б) 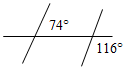 г)
г)
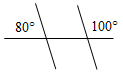
А7. На рисунке прямые т, п, k пересечены секущей р. Параллельными прямыми будут…
а) т и п; б) т и k; в) п и k; г) т, п и k.
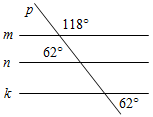
А8. Верным является высказывание:
а) Если при пересечении двух параллельных прямых секущей соответственные углы равны, то прямые параллельны.
б) Если прямая пересекает одну из параллельных прямых, то она перпендикулярна другой.
в) Если две параллельные прямые пересечены секущей, то сумма соответственных углов равна 180°.
г) Если две параллельные прямые пересечены секущей, то однородные углы равны.
Часть 2
В1. Прямые т и п, изображенные на рисунке, являются ______________________________________________
![]()
В2. Из всех углов, изображенных на рисунке, соответственными являются углы __________________________
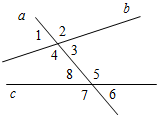
В3. Прямые т и п параллельны. Тогда сумма Ð2 и Ð3 будет равна ______________________________________
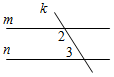
В4. На рисунке прямые т и п – параллельны, Ð3 = 112°. Тогда Ð1 = ____________________________________
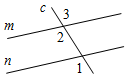
В5. На рисунке т || п, Ð2 на 40° меньше Ð3. Тогда Ð1 = ______________________________________________
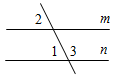
В6. На рисунке прямые с и d – параллельны, Ð2 = 50°, Ð3 = 84°. Тогда Ð1 = ______________________________
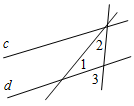
В7. На рисунке через вершину С треугольника АВС проведена прямая KL, параллельная стороне треугольника АВ. При этом ÐACK = 61°, ÐBCL = 63°. Тогда сумма углов треугольника АВС будет равна ____________________
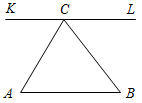
Часть 3
С1. Отрезок МР – биссектриса треугольника MNK. Через точку Р проведена прямая, параллельная стороне MN и пересекающая сторону MK в точке Е. Вычислите градусные меры углов треугольника МРЕ, если ÐNMK = 84°.
Ответы:
Часть 1
|
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
А8 |
|
б |
б |
в |
б |
б |
г |
г |
а |
Часть 2
|
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
|
Параллельными |
3 и 6, 2 и 5, 1 и 8, 4 и 7 |
180° |
68° |
70° |
34° |
180° |
Часть 3
Возможный вариант оформления решения задачи.
С1.
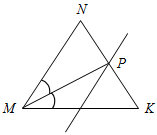
1. ÐMNK и ÐРЕМ являются односторонними при параллельных прямых MN и РЕ и секущей MK, поэтому сумма их равна 180°, а значит, ÐРЕМ = 96°.
2. МР – биссектриса треугольника, поэтому ÐNMР = ÐРMK = 42°.
3. ÐNMР = ÐМРЕ – накрест лежащие при параллельных прямых MN и РЕ и секущей MР, а так как внутренние накрест лежащие углы при параллельных прямых MN и РЕ равны, то ÐМРЕ = 42°.
4. Так образом, ÐМРЕ = ÐЕМР = 42°, ÐМЕР = 96°.
Урок66. Повторение.
Соотношения между сторонами и углами треугольника
|
Цели деятельности учителя |
Создать условия для приведения в систему знаний, умений, навыков по теме «Соотношения между сторонами и углами треугольника»; совершенствовать навыки решения задач |
|
|
Термины и понятия |
Параллельные прямые, аксиома параллельности, накрест лежащие углы, соответственные углы, односторонние углы |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы, контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: осознают важность и необходимость изучения предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для математического диктанта. • Тест |
|
|
I этап. Актуализация опорных знаний учащихся |
||||||||||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||||||||||
|
Ситематизировать |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Математический диктант с взаимопроверкой. Тексты раздаются каждому учащемуся. На работу дается 3 минуты. После этого на экран выводятся правильные ответы. – Закончите предложения. • Сумма углов треугольника равна … • Треугольник, у которого есть прямой угол, называется ... • Гипотенузой прямоугольного треугольника называется ... другие стороны называются ... • Треугольник, в котором все три угла острые, называется ... • Треугольник, в котором один угол тупой, называется ... • Угол, смежный с внутренним углом треугольника, называется ... • Внешний угол треугольника равен ... • В треугольнике против большего угла лежит ... сторона, а против большей стороны лежит ... угол. • В прямоугольном треугольнике ... больше катета. • Если два угла треугольника равны, то треугольник ... • Каждая сторона треугольника меньше ... • Сумма двух острых углов прямоугольного треугольника равна ... • Катет прямоугольного треугольника ... равен половине гипотенузы. • Если катет прямоугольного треугольника ... то угол ... равен 30° |
|||||||||||||||
|
II этап. Тест |
||||||||||||||||
|
Цель деятельности |
Тестовые задания |
|||||||||||||||
|
Проверить умение |
(И) Учащиеся выполняют тестовые задания (см. Ресурсный материал). Методические указания: Время на выполнение – 35–40 минут (если часть 3 не предлагается, то время уменьшить до 20–25 минут). Нормы отметок: «5» – 18–20 баллов; «4» – 15–17 баллов; «3» – 11–14 баллов; «2» – 0–10 баллов. Рекомендации по оцениванию решения задания С1 части 3:
|
|||||||||||||||
|
III этап. Итоги урока. Рефлексия |
||||||||||||||||
|
Деятельность учителя |
Деятельность учащихся |
|||||||||||||||
|
(Ф/И) – Оцените свою работу на уроке и работу своего товарища |
(И) Домашнее задание: решить № 335 |
|||||||||||||||
Ресурсный материал
Тест
Часть 1
А1. Тупоугольный треугольник изображен на рисунке:
а)  б)
б)  в)
в)  г)
г) 
А2. Гипотенузой треугольника АВС, изображенного на рисунке, является сторона…
а) АВ; б) ВС; в) АС; г) АВ и АС.
А3. В треугольнике MNK наибольшей стороной является…
а) MN; б) MK; в) KN; г) NK и MN.
А4. Равнобедренным является треугольник, изображенный на рисунке…
а)  б)
б) 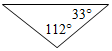 в)
в) 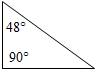 г)
г) 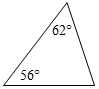
А5. Две стороны треугольника равны 2 см и 3 см. Тогда третья сторона треугольника может быть равна…
а) 6 см; б) 5 см; в) 3 см; г) 1 см.
А6. В треугольнике MNK один из углов тупой. Другие два угла треугольника могут быть…
а) только острыми; в) один тупым, другой острым;
б) один острым, другой прямым; г) один прямым, другой тупым.
Часть 2
В1. На рисунке прямоугольными являются треугольники _____________________________________________

В2. Меньшей стороной треугольника АВС является __________________________________________________
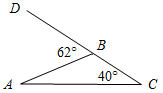
В3. На рисунке Ð1 = ___________________________________________________________________________
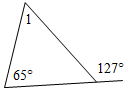
В4. Величина одного из углов равнобедренного треугольника равна 70°. Тогда другие углы треугольника будут равны _________________________________________________________________________________________
В5. На рисунке ÐАВЕ = 104°, ÐАСВ = 76°, АС = 12 см. Тогда сторона АВ треугольника АВС будет равна ______________________________________________________________________________________________________
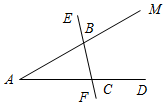
В6. В равностороннем треугольнике АВС проведены биссектрисы AD и BF, которые пересекаются в точке О. Тогда углы треугольника AOF будут равны ___________________________________________________________
В7. На чертеже величина угла С равна _____________________________________________________________
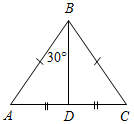
В8. В треугольнике АВС медиана ВD в 2 раза меньше стороны АС. Угол В треугольника АВС равен ___________
В9. В треугольнике АВС угол А больше угла В на 40°, а угол С меньше угла А на 20°. Тогда ÐВ = _____________
Часть 3
С1. В треугольнике АВС угол С равен 90°, а угол В равен 70°. На катете АС отложен отрезок CD, равный СВ. Найдите углы треугольника ABD.
Ответы:
Часть 1
|
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
|
а |
б |
в |
г |
в |
а |
Часть 2
|
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
В8 |
В9 |
|
KMN, HSL |
BC |
62° |
70°, 40° или 55°, 55° |
12 см |
30°, 30°, 120° |
60° |
90° |
40° |
Часть 3
Возможный вариант оформления решения задачи.
С1.
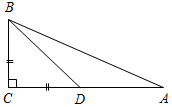
1. Так как в треугольнике АВС сумма углов равна 180°, то ÐА = 20°.
2. Так как ВС = CD, то прямоугольный треугольник BCD
является равнобедренным, поэтому ÐCBD = ÐCDB =
= 45°.
3. Углы BDC и АDB являются смежными, а так как сумма смежных углов равна 180°, то ÐBDА = 135°.
4. В треугольнике АBD: ÐBDА = 135°, ÐDАB = 20°, поэтому ÐАBD = 25°.
5. Таким образом, углы треугольника АBD будут равны: ÐBDА = 135°, ÐDАB = 20°, ÐАBD = 25°.
Урок67. Повторение.
Соотношения между сторонами и углами треугольника
|
Цели деятельности учителя |
Создать условия для приведения в систему знаний, умений, навыков по теме «Соотношения между сторонами и углами треугольника»; совершенствовать навыки решения задач |
|
|
Термины и понятия |
Параллельные прямые, аксиома параллельности, накрест лежащие углы, соответственные углы, односторонние углы |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, результаты, методы для решения задач практического характера |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют познавательный интерес к изучению предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И); групповая (Г) |
|
|
Образовательные |
• Чертежи к задачам |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Привести в систему знания по теме |
(Ф/И) Проверить правильность выполнения домашнего задания. № 335. Решение: а) В DАВС по условию ÐА + ÐВ> 90°, а так как ÐА + ÐВ + ÐС = 180°, то ÐС< 90°. Так же можно получить, что ÐА< 90°, ÐВ< 90°, то есть DАВС – остроугольный. б) В DАВС по условию ÐА<ÐВ + ÐС, а так как ÐВ + ÐС = 180° – ÐА, то ÐА< 180° – ÐА, ÐА< 90°. Аналогично можно получить, что ÐВ< 90°, ÐС < 90°, тогда DАВС – остроугольный
Рис. 1 |
|
|
II этап. Решение по готовым чертежам |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить умение применять теоретические знания в решении задач |
(П) Рисунки начертить в тетрадях и на них записать промежуточные результаты. Записать ответы. 1. Дано:ÐС = 50°, ÐА на 20° больше ÐВ. 2. Дано:ÐA : ÐB : ÐC = 11 : 4 : 3. Найти:ÐA, ÐB. Найти:ÐA, ÐB, ÐC.
Рис. 2 Рис. 3 Ответ: ÐA = 15°, ÐB = 55°. Ответ:ÐA = 110°, ÐB = 40°, ÐC = 30°. 3. Дано:ÐA в 1,5 раза меньше ÐВ. 4. Найти: ÐA, ÐC. Найти:ÐA, ÐВ.
Рис. 4 Рис. 5 Ответ: ÐA = 36°, ÐB = 54°. Ответ: ÐA = 65°, ÐC = 65°. 5. Найти:ÐACD. 6. Найти:ÐB. 7. Найти: АС.
Рис. 6 Рис. 7 Рис. 8 Ответ:ÐACD = 140°. Ответ: ÐB = 70°. Ответ: АС = 15. 8. Найти: АВ. 9. Дано: СЕ – биссектриса. 10. Дано: АВ = ВС. Найти:ÐA, ÐB. Найти:ÐB.
Рис. 9 Рис. 10 Рис. 11 Ответ: АВ = 16. Ответ: ÐA = 65°, ÐB = 25°. Ответ: ÐB = 40°. 11. Найти:ÐDFE. 12. Найти:ÐBAD. 13. Дано: СЕ – медиана. Найти:ÐA, ÐВ.
Рис. 12 Рис. 13 Рис. 14 Ответ:ÐDFE = 130°. Ответ:ÐBAD = 50°. Ответ: ÐA = 53°, ÐВ = 37°. 14. Найти:ÐВ. 15. Найти:ÐАВС.
Рис. 15 Рис. 16 Ответ: ÐB = 80°. Ответ: ÐАВС = 135° |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Оцените свою работу и работу своего соседа по парте. – Какие трудности возникли при решении задач? |
(И) Домашнее задание:
повторить § 4 (глава IV); прочитать тему «Задачи |
|
Урок68. Повторение. Задачи на построение
|
Цель деятельности учителя |
Создать условия для повторения основных задач на построение; совершенствовать навыки решения задач на построение |
|
|
Термины и понятия |
Построение угла, равного данному, построение биссектрисы угла, построение перпендикулярных прямых, середины отрезка |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, результаты, методы для решения задач практического характера |
Познавательные: умеют планировать и осуществлять деятельность, направленную на решение задач исследовательского характера. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют познавательный интерес к изучению предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для индивидуальной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Повторить основные |
(Ф/И) 1. Шесть учеников выполняют у доски следующие задания: 1) на данном луче от его начала отложить отрезок, равный данному; 2) отложить от данного луча угол, равный данному; 3) построить биссектрису данного неразвернутого угла; 4) построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка; 5) построить середину данного отрезка; 6) построить прямую, проходящую через данную точку и перпендикулярную к прямой, не проходящей через данную точку. 2. Пока учащиеся у доски готовятся, класс выполняет дифференцированные задания. Построить треугольник: 1) по двум сторонам и углу между ними; 2) по стороне и прилежащим к ней углам; 3) по трем сторонам |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 353 2. Решить самостоятельно
задачи № 354, 360, 362 |
№ 353. Анализ(см. рис.1):
Рис. 1 Пусть X – искомая
точка, то есть АХ = ХВ, тогда ∆АХВ –
равнобедренный и XY – План построения: 1) Построить точку Y – середину АВ. 2) Построить прямую, проходящую через Y и перпендикулярную АВ. 3) Прямая b пересекается с окружностью в точках Х и Z. Х и Z – искомые точки. Построение(см. рис. 2):
Рис. 2 Доказательство: ∆AYX = ∆BYX по двум катетам (они
прямоугольные, так как Исследование: Задача может иметь: а) два решения (см. план построения и построение); б) одно решение, если прямая b имеет одну общую точку с окружностью (касается ее) (рис. 3); в) ни одного решения, если прямая b не имеет общих точек с окружностью (рис. 4).
Рис. 3 Рис. 4 № 354. Соединяем точки А, В
и С. Находим середины отрезков АВ, ВС и АС,
соответственно K, L и М. Проводим перпендикуляры
(серединные перпендикуляры DАВС). Вокруг треугольника всегда можно описывать окружность, поэтому задача не имеет решения, лишь когда точки лежат на одной прямой.
Рис. 5 № 360.
Рис. 6 Проводим прямую а. Отмечаем на ней точку А – одну из вершин нашего треугольника, на прямой откладываем отрезок, равный периметру треугольника. На прямой b откладываем отрезок АН, равный высоте треугольника. Строим заданный Ða с вершиной в точке А. Проводим прямую с^b, Н^с. Обозначим точку пересечения с со стороной Ða – В. От точки K откладываем на прямой а отрезок, равный АВ – KC. Соединяем В и С. АВС – искомый треугольник. № 362.
а) Рис. 7 б) Пусть надо построить DАВС, и даны ÐPQR и отрезки В1С1,
равный стороне треугольника, и MN, равный сумме двух других сторон
треугольника (см. рис. а). Проведем произвольную прямую а,
отметим на ней точку В и точку Х(см. рис. б). ÐKAB = ÐАВС + ÐАСВ (как внешний). DKAB – равнобедренный (так как ÐBKA = ÐKBA по построению). Значит, ÐKBA = ÐKBС = ÐKBA + ÐАВС =
ÐLBC = 2ÐKBС = 180° + ÐАВС – ÐАСВ (так как BK – биссектриса угла LBC). ÐPQR = ÐXBL = 180° – ÐLBC = 180° – 180° – ÐАВС + ÐАСВ = ÐАСВ – ÐАВС. АВ = AK, так как DKBA – равнобедренный, значит, MN
= KA + АС = АВ + АС, |
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какой этап в задачах на построение у вас вызывает наибольшее затруднение? – Оцените свою работу на уроке |
(И) Домашнее задание: решить задачи № 352, 356, 361 (одну задачу решить по полной схеме) |
|
Уроки69–70. Итоговый контрольный тест
|
Цели деятельности учителя |
Создать условия для приведения в систему знаний, умений, навыков за курс геометрии 7 класса; совершенствовать навыки решения задач |
|
|
Термины и понятия |
Углы, равнобедренный треугольник, прямоугольный треугольник, высота, медиана, биссектриса, параллельные прямые |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость знаний в жизни человека |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные |
• Задания для теста |
|
|
I этап. Актуализация опорных знаний |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить правильность выполнения домашней работы |
(Ф/И) Ответить на вопросы по домашнему заданию |
|
|
II этап. Итоговый тест (с взаимопроверкой) |
||
|
Цель деятельности |
Тестовые задания |
|
|
Проверить уровень сформированности теоретических знаний учащихся за курс 7 класса и умение применять полученные знания при решении задач |
(И) Учащиеся выполняют тестовые задания (см. Ресурсный материал) |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
– Оцените работы. – Составьте синквейн к изученному за 7 класс материалу |
Домашнее задание: отработать
задачи, вызвавшие наибольшие затруднения |
|
Ресурсный материал
Тест
1. Прямые т и п параллельны, k – секущая. По данным рисунка 1 найдите значение у.
2. По данным рисунка 2 найдите PK, если расстояние между прямыми МK и РТ равно 10 см.
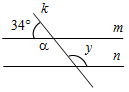
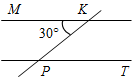
Рис. 1 Рис. 2
3. Отрезки MN и KB пересекаются в точке А. Точка А является серединой отрезка KB, и угол AKN равен углу АВМ. Найдите угол KNA, если угол ВМА равен 53°.
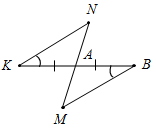
Рис. 3
4. (Задание оценивается в 4 балла.)
В равнобедренном треугольнике АВСАВ = АС. Прямая PF пересекает боковые стороны АВ и АС в точках P и F соответственно. Длина отрезка АР равна 31 дм. Угол В треугольника АВС равен углу АPF. Найдите длину отрезка АР.
5. (Задание оценивается в 5 баллов.)
Укажите номера верных утверждений.
1) Катет прямоугольного треугольника является высотой.
2) Вертикальные углы равны.
3) В треугольнике против угла в 87° лежит бо́льшая сторона.
4) Если даны две параллельные прямые, то третья прямая всегда их пересекает.
5) У любого треугольника больше одного острого угла.
6. (Задание оценивается в 6 баллов.)
В равнобедренном треугольнике MNK с основанием NM проведена медиана KD. Найдите углы треугольника KDМ и угол MKN, если внешний угол треугольника MNK при вершине N равен 130°.
Ответы: 1 – 146°; 2 – 20 см; 3 – 53°; 4 – 31 см; 5 – 1, 2, 5; 6 – 90°, 50°, 40°, 80°.
Пояснительная записка
Настоящая рабочая программа разработана в соответствии с основными положениями федерального государственного образовательного стандарта и требованиями Примерной образовательной программы основного общего образования, с учетом основных идей и положений Программы развития и формирования универсальных учебных действий и ориентирована на использование учебно-методического комплекта:
1. Геометрия. 7–9 классы : учеб. для общеобразоват. организаций / Л. С. Атанасян [и др.]. – М. : Просвещение, 2014.
2. Геометрия. 7 класс. Рабочая тетрадь : пособие для учащихся общеобразоват. организаций / Л. С. Атанасян [и др.]. – М. : Просвещение, 2014.
3. Геометрия. Сборник рабочих программ. 7–9 кл. / сост. Т. А. Бурмистрова. – М. : Просвещение, 2013.
4. Зив, Б. Г. Геометрия : дидактические материалы : 7 кл. / Б. Г. Зив, В. М. Мейлер. – М. : Просвещение, 2013.
5. Изучение геометрии в 7–9 классах : метод. рекомендации : кн. для учителя / Л. С. Атанасян [и др.]. – М. : Просвещение, 2011.
6. Мищенко, Т. М. Геометрия : тематические тесты : 7 кл. / Т. М. Мищенко, А. Д. Блинков. – М. : Просвещение, 2013.
Дополнительная литература для учителя:
7. Звавич, Л. И. Контрольные и проверочные работы по геометрии. 7–9 классы / Л. И. Звавич [и др.]. – М., 2001.
8. Зив, Б. Г. Задачи по геометрии : пособие для учащихся 7–11 классов общеобразоват. организаций / Б. Г. Зив, В. М. Мейлер, А. Г. Баханский. – М. : Просвещение, 2014.
9. Кукарцева, Г. И. Сборник задач по геометрии в рисунках и тестах. 7–9 классы / Г. И. Кукарцева. – М., 1999.
10. Саврасова, С. М. Упражнения по планиметрии на готовых чертежах / С. М. Саврасова, Г. А. Ястребинецкий. – М., 1987.
11. Фарков, А. В. Диагностические контрольные работы по геометрии. 7 класс / А. В. Фарков. – М., 2009.
Дополнительная литература для учащихся:
12. Шуба, М. Ю. Занимательные задания в обучении математике / М. Ю. Шуба. – М., 1997.
13. Энциклопедия для детей : в 15 т. Т. 11. Математика / под ред. М. Д. Аксенова. – М. : Аванта+, 1998.
При работе можно использовать также статьи из научно-теоретического и методического журнала «Математикав школе», из еженедельного учебно-методического приложения к газете «Первое сентября» «Математика».
Согласно действующему учебному плану рабочая программа предусматривает обучение в объеме 70 часов, 2 часа в неделю, втом числе для проведения:
– контрольных работ – 5 учебных часов;
– самостоятельных работ – 4 учебных часа;
– проектной деятельности – 5 учебных часов;
– исследовательской деятельности – 4 учебных часа.
С учетом уровневой специфики класса выстроена система учебных занятий (уроков), спроектированы цели, задачи, ожидаемые результаты обучения.
Требования к уровню подготовки учащихся 7
класса
(базовый уровень)
Должны знать:определение точки, прямой, отрезка, луча, угла; единицы измерения отрезка, угла; определение вертикальных и смежных углов, их свойства; определение перпендикулярных прямых; определение треугольника, виды треугольников, признаки равенства треугольников, свойства равнобедренного треугольника, определение медианы, биссектрисы, высоты; определение параллельных прямых, их свойства и признаки; соотношение между сторонами и углами треугольника, теорему о сумме углов треугольника; определение прямоугольного треугольника, его свойства и признаки.
Должны уметь: обозначать точки, отрезки и прямые на рисунке, сравнивать отрезки и углы, с помощью транспортира проводить биссектрисуугла; изображать прямой, острый, тупой и развернутый углы; изображать треугольники и находить их периметр; строить биссектрису, высоту и медиану треугольника; доказывать признаки равенства треугольников; показывать на рисунке пары накрест лежащих, соответственных, односторонних углов, доказывать признаки параллельности двух прямых; доказывать теорему о сумме углов треугольника; знать, какой угол называется внешним углом треугольника; применять признаки прямоугольных треугольников к решению задач; строить треугольники по трем элементам.
Должны владеть компетенциями:познавательной,коммуникативной, информационной и рефлексивной.
Способны решать следующие жизненно-практические задачи:самостоятельно приобретать и применять знания в различных ситуациях, работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов, пользоваться предметным указателем энциклопедий и справочником для нахождения информации, самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем.
Информационно-методическое
обеспечение
учебного процесса
1. Программно-педагогические средства, реализуемые с помощью компьютера.
1. CD «1С: Репетитор. Математика» (КиМ).
2. CD «Уроки геометрии. 7–9 классы» (в 2 ч.) (КиМ).
3. CD «ГЕОМЕТРИЯ не для отличников» (НИИ экономики авиационной промышленности).
4. CD «Математика. 5–11 классы. Практикум».
2. Цифровые образовательные ресурсы (ЦОР) для поддержки подготовки школьников.
1. Интернет-портал Всероссийской олимпиады школьников. – Режим доступа : http://www.rusolymp.ru
2. Всероссийские дистанционные эвристические олимпиады по математике. – Режим доступа : http://www.eidos.ru/olymp/mathem/index.htm
3. Информационно-поисковая система «Задачи». – Режим доступа : http://zadachi.mccme.ru/easy
4.Задачи: информационно-поисковая система задач по математике. – Режим доступа : http://zadachi.mccme.ru
5. Конкурсные задачи по математике: справочник и методы решения. – Режим доступа : http://mschool.kubsu.ru/cdo/shabitur/kniga/tit.htm
6. Материалы (полные тексты) свободно распространяемых книг по математике. – Режим доступа : http://www.mccme.ru/free-books
7. Математика для поступающих в вузы. – Режим доступа : http://www.matematika.agava.ru
8. Выпускные и вступительные экзамены по математике : варианты, методика. – Режим доступа : http://www.mathnet.spb.ru
9. Олимпиадные задачи по математике : база данных. – Режим доступа : http://zaba.ru
10. Московские математические олимпиады. – Режим доступа : http://www.mccme.ru/olympiads/mmo
11. Школьные и районные математические олимпиады в Новосибирске. – Режим доступа : http://aimakarov.chat.ru/school/school.html
12. Виртуальная школа юного математика. – Режим доступа : http://math.ournet.md/indexr.htm
13. Библиотека электронных учебных пособий по математике. – Режим доступа : http://mschool.kubsu.ru
14. Образовательный портал «Мир алгебры». – Режим доступа : http://www.algmir.org/index.html
15. Словари БСЭ различных авторов. – Режим доступа : http://slovari.yandex.ru
16. Этюды, выполненные с использованием современной компьютерной 3D-графики, увлекательно и интересно рассказывающие о математике и ее приложениях. – Режим доступа : http://www.etudes.ru
17. Заочная физико-математическая школа. – Режим доступа : http://ido.tsu.ru/schools/physmat/index.php
18. Министерство образования РФ. – Режим доступа : http://www.ed.gov.ru; http://www.edu.ru
19. Тестирование on-line. 5–11 классы. – Режим доступа : http://www.kokch.kts.ru/cdo
20. Архив учебных программ информационного образовательного портала «RusEdu!». – Режим доступа : http://www.rusedu.ru
21. Мегаэнциклопедия Кирилла и Мефодия. – Режим доступа : http://mega.km.ru
22. Сайты энциклопедий. – Режим доступа : http://www.rubricon.ru; http://www.encyclopedia.ru
23. Вся элементарная математика. – Режим доступа : http://www.bymath.net
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
|
Глава 1. Начальные геометрические сведения (12 часов) |
|
|
Модуль 1. Прямая, отрезок, луч |
|
|
Цели ученика: – овладение знанием основных понятий темы: прямая, отрезок, луч, длина отрезка, начало луча, равные отрезки, пересекающиеся прямые; – совершенствование умений чертить изучаемые фигуры, обозначать их, измерять длину отрезков, записывать результаты измерений; –
освоение навыка проведения сравнения математических объектов (сравнения
отрезков по величине) способом наложения |
Цели педагога: –
создание условий для систематизации и обобщения имеющихся – организация познавательной деятельности на уроках с целью овладения практическими навыками построения прямых, отрезков, лучей, способами их обозначения, навыками сравнения отрезков; – разработка заданий, позволяющих организовать деятельность учащихся по овладению общими приемами сравнения геометрических фигур (на примере сравнения простейших фигур – отрезков), формированию начальной геометрической культуры |
|
Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://mega.km.ru; самообразование и самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 1, вариант 1 (в рамках ЦДО) |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
Предмет «геометрия» (комбинированный) |
[1]*, п. 1, 2, вопросы 1–3 к гл. I, практич. задания № 1–7 |
Регулятивные: учитывать правило в планировании и контроле способа решения. Познавательные: использовать поиск необходимой информации для выполнения учебных заданий с использованием учебной ли-тературы. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве |
Знание: – основных понятий темы: прямая, отрезок, граничная точка отрезка (репродуктивно-алгоритмическое); – построения с помощью чертежной линейки
прямых и отрезков, называние их с помощью принятых условных обозначений (продуктивно-комбинаторное); Умение:задавать
вопросы Приобретенная компетентность: предметная, целостная |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Специально организованное общение |
Учебно-познавательная |
Фронтальная, индивидуальная |
Портреты ученых-математиков, демонстрационная линейка |
|
2 |
Прямая и отрезок (комбинированный) |
Традиционно-педагогическая. Объяснительно-ил-люстра- тивная |
Специально организованное общение |
Учебно-познавательная |
Фронтальная, индивидуальная |
[2] |
|||
|
3 |
Сравнение отрезков (комбинированный) |
[1], п. 6, 7, вопросы 12–13 |
Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок. Познавательные: строить
Коммуникативные: контролировать действия партнера |
Знание: – основных понятий темы: отрезок, граничная точка отрезка, длина отрезка, часть отрезка, единицы измерения длины (миллиметр, сантиметр, метр, километр) (репродуктивно-алгоритмическое); – построения с помощью чертежной линейки отрезков, измерения их длины, записи измерения с помощью принятых условных обозначений; перехода одной единицы измерения длины в другую, нахождения длины отрезка, если известны длины его частей (продуктивно-комбинаторное); – сведений, обобщенных в презентации, о различных единицах измерения длин, их эволюции (продуктивно-креативное). Умение: провести
исследо-вания несложных ситуаций Приобретенная компетентность: целостная, предметная, учебно-познавательная |
Развивающее образование. Поисковая |
Организация совместной учебной деятельности |
Учебно-познавательная |
Групповая |
Таблица «Единицы измерения длин», демонстрационная линейка, рулетка, штангенциркуль |
|
4 |
Измерение отрезков (комбинированный) |
Развивающее образование. Поисковая |
Учебно-познавательная |
Групповая |
[2]. [8] § 1, варианты 1–4. [8] § 2, задача № 1 |
||||
|
5 |
Измерение отрезков (применение и совершенствование знаний) |
[8] § 1, варианты 5–6. [1], п. 6, 7, вопросы 4–6 к гл. I, практические задания № 8–13 |
Регулятивные: различать способ и результат действия. Познавательные: ориентироваться
на разнообразие способов решения Коммуникативные: контролировать действия партнера |
Компетентностно-ориентированная. Исследовательская |
Лабораторно-графическая |
Учебно-познавательная |
Парная (взаимопроверка) |
Разноуровневые задания, ручки разного цвета (для взаимопроверки), бумага для черчения, линейки |
|
|
6 |
Луч (применение и совершенствование знаний) |
Знание: – основных понятий темы: луч, начало луча (репродуктивно-алгоритмическое); – построения с помощью чертежной линейки геометрической фигуры луч, называния их с помощью принятых условных обозначений (продуктивно-комбинаторное); – сведений, обобщенных в презентации, о возникновении и значении термина «луч» (продуктивно-креа- тивное). Умение:задавать вопросы к наблюдаемым фактам, обозначать свое понимание или непонимание изучаемого материала, овладевать азами графической культуры (построение лучей). Приобретенная компетентность: предметная, целостная |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Специально организованное общение |
Учебно-познавательная |
Фронтальная, индивидуальная |
Таблица «Луч». [8] § 2, задачи № 1 |
|
Глава 1. Начальные геометрические сведения |
|
|
Модуль 2. Угол |
|
|
Цели ученика: – овладение знанием основных понятий темы: угол, вершина угла, стороны угла, градусная мера угла, острый угол, тупой угол, развернутый угол, вертикальные углы, смежные углы, свойство смежных и вертикальных углов; – совершенствование умений чертить изучаемые фигуры, обозначать их, измерять градусную меру угла, записывать результаты измерений; – совершенствование навыка проведения сравнения математических объектов (сравнение углов по величине) способом наложения и с помощью измерений, классификации объектов по признакам, выделенным в определении геометрических фигур (на примере классификации углов по их видам) |
Цели педагога: – создание условий для систематизации и
обобщения имеющихся – организация познавательной деятельности на уроках с целью овладения практическими навыками построения углов, способами их обозначения, измерения градусной меры углов; – разработка заданий, позволяющих организовать деятельность учащихся по овладению общими приемами сравнения геометрических фигур (на примере сравнения углов), формированию начальной геометрической культуры |
|
Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://www.uic.ssu.samara.ru/~nauka/; самообразование и самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 1, вариант 2 (в рамках ЦДО) |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
7 |
Угол |
[1], п. 4, 6, 9, вопросы 5–6, 10–11 к гл. I, практические задания № 41–44 |
Регулятивные: различать способ и результат действия. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: угол, вершина угла, стороны угла, внутренняя область угла, биссектриса угла, равные фигуры (репродуктивно-алгоритмическое); – построения с помощью чертежной линейки углов, называния с помощью принятых условных обозначений сторон угла и вершины, сравнения углов наложением (продуктивно-комбинаторное); – сведений, обобщенных в презентации, о происхождении термина «биссектриса» (продуктивно-креа- тивное). Умение: проводить
исследования несложных ситуаций Приобретенная компетентность: целостная, предметная, учебно-познавательная |
Развивающее образование. Поисковая |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая |
[8] § 2, задачи № 2 |
|
8 |
Сравнение и измерение углов (комбинированный) |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Познавательная, информационно-коммуникационная |
Групповая |
[2]. [4] § 3, задачи № 1 |
||||
|
9 |
Измерение углов ствование знаний) |
[1], п. 9, 11, вопросы практические задания № 55–56 |
Регулятивные: различать способ и результат действия. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: градусная мера угла, острые, тупые, прямые, развернутые, смежные, вертикальные углы (репродуктивно-алгоритмическое); – построения с помощью чертежной линейки углов, измерения их величины с помощью транспортира, записи измерения с помощью принятых условных обозначений, построения углов заданной величины, определения вида угла, применения свойств смежных и вертикальных углов (продуктивно-комбинаторное). Умение: проводить измерительные работы, классификацию по выделенному признаку (на примере определения вида углов), сравнивать объект наблюдения (угол) с эталоном (прямым углом). Приобретенная компетентность: целостная, предметная, учебно-познавательная |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Специально организованное общение |
Учебно-познавательная |
Фронтальная, индивидуальная |
Демонстрационный транспортир. Таблица «Измерение углов». [8] § 4, задачи № 2 |
|
10 |
Смежные и вертикаль- ные углы (комбинированный) |
Компетентностно-ориентированная. Исследовательская |
Теоретическое исследование |
Учебно-познавательная |
Фронтальная, индивидуальная |
Упражнения по планимет- рии на готовых чертежах: [10], таблица № 1. [2] |
|||
|
11 |
Перпендикулярные прямые |
[1], п. 12, вопросы 18–21 к гл. I, практические задания № 57 |
Регулятивные: различать способ и результат действия. Познавательные: использовать
поиск необходимой информации для выполнения учебных заданий Коммуникативные: контролировать действия партнера |
Знание: – основных понятий темы: перпендикулярные прямые, способы построения перпендикулярных прямых на местности (репродуктивно-алгоритмическое); – построения с помощью чертежного угольника перпендикулярных прямых углов, записи факта перпендикулярности прямых с помощью принятых условных обозначе- ний(продуктивно-комбинаторное). Умение: переводить текстовую информацию в графический образ и математическую модель, решать комбинированные задачи с использованием 1–2 алгоритмов, запи-сывать решения с помощью принятых условных обозна-чений. Приобретенная компетентность: предметная |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Специально организованное общение |
Учебно-познавательная |
Фронтальная, индивидуальная |
Таблица [2] |
|
12 |
Контрольная работа по теме «Начальные геометрические сведения» (контроль и оценка знаний) |
Контрольно-оценочная. Поисковая |
Самостоятельное планирование
и проведение |
Рефлексивная |
Индивидуальная |
[8], контрольная работа № 1. Дифференцированный |
|
Глава 2. Треугольники (18 часов) |
|
|
Модуль 1. Первый признак равенства треугольников |
|
|
Цели ученика: – овладение знанием основных понятий темы: равные треугольники, теорема-признак, соответственные элементы, первый признак равенства треугольников; – освоение умения доказывать равенство треугольников с помощью первого признака равенства треугольников; – совершенствование умения пользоваться математической символикой при записи условия и доказательства теоремы, умения проводить доказательные рассуждения |
Цели педагога: – создание условий для формирования у учащихся представлений о понятии «теорема», «теорема-признак»; – организация познавательной деятельности на уроках с целью овладения алгоритмом выявления равных треугольников с помощью первого признака равенства треугольников; – разработка заданий, позволяющих организовать деятельность учащихся по овладению общими приемами доказательства теорем (умением выделять в теореме условие и заключение), умением проводить доказательные рассуждения |
|
Внеурочная деятельность:
поиск информации с использованием интернет-ресурсов: http://mega.km.ru;
http://www.rubricon.ru; |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
13 |
Треугольники (изучение нового материала) |
[1], п. 14, 15, вопросы 1–4 к гл. II, практические задания № 87–89 |
Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Познавательные: использовать поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы |
Знание: – основных понятий темы: треугольник, вершина, сторона, угол треугольника, периметр треугольника, равные треугольники, соответственные элементы, первый признак равенства треугольников (репродуктивно-алгоритмическое); – построения треугольников, проведения измерений его элементов, записи результатов измерений, нахождения периметра; – перевода текста (формулировки) первого признака равенства треугольников в графический образ, короткой записи, проведения доказательства, применения для решения задач на выявление равных треугольников (продуктивно-комбинаторное); – презентация «Треугольники вокруг нас» (продуктивно-креативное). Умение: – переводить текстовую информацию в графический образ и математическую модель, представлять информацию в сжатом виде – схематичной записи формулировки теоремы; – проводить доказательные рассуждения,
понимать специфику математического Приобретенная компетентность: предметная |
Развивающее образование. Поисковая |
Беседа, демонстрация |
Учебно-познавательная |
Фронтальная, индивидуальная |
Таблицы «Равные треугольники», «Признаки равенства треугольников» |
|
14 |
Первый признак равенства треугольников (комбинированный) |
Развивающее образование. Поисковая |
Проблемные задачи |
Учебно-познавательная |
Фронтальная, индивидуальная |
[2]. [8] § 7, вари- анты 1–3. Модели треугольников |
|||
|
15 |
Первый признак равенства треугольников (применение и совершенствование знаний) |
[1], п. 15– практические задания № 100– |
Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Познавательные: строить
Коммуникативные: контролировать действия партнера |
Традиционно-педагогическая. Поисковая |
Практикум |
Познавательная, информационно-коммуникационная |
Групповая |
Упражнения по планимет- рии на готовых чертежах: [4], таблица № 2. [8] § 7, вари- анты 4–8 |
|
|
16 |
Медиана, биссектриса и высота треугольника (изучение нового материала) |
Знание: – основных понятий темы: – построения с помощью чертежного угольника и транспортира медианы, высоты, биссектрисы прямоугольного треугольника (продуктивно-комбинаторное); – сведений, обобщенных Умение:грамотно выполнять алгоритмические предписания и инструкции (на примере построения медиан, высот, биссектрис треугольника), овладевать азами графической культуры. Приобретенная компетентность: предметная, учебно-познавательная |
Развивающее образование. Поисковая |
Лабораторно-графическая |
Учебно-познавательная |
Фронтальная, индивидуальная |
[8] § 8, задачи № 1. [2] |
||
|
17 |
Свойства равнобедренного треугольника (комбинированный) |
[1], п. 18, вопросы 10– практические задания № 104 |
Регулятивные: Познавательные: владеть
общим приемом решения задач; ориентироваться на разнообразие способов
решения Коммуникативные: договариваться
и приходить к общему решению в совместной деятельности, в том числе в
ситуации столкновения интересов; контролировать действия |
Знание: – основных понятий темы: равнобедренный треугольник, основание, боковые стороны, равносторонний треугольник (репродуктивно-алгоритмическое); – доказательства и применения при решении теоремы о свойствах равнобедренного треугольника (продуктивно-комбинаторное). Умение: проводить
исследования несложных ситуаций Приобретенная компетентность: целостная, предметная, учебно-познавательная |
Компетентностно-ориентированная. Исследовательская |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая |
Упражнения по планимет- рии на готовых чертежах: [10], таблица № 3. [8] § 8, задачи № 2 |
|
18 |
Свойства равнобедренного треугольника (комбинированный) |
Компетентностно-ориентированная. Исследовательская |
Познавательная, информационно-коммуникационная |
Групповая |
Упражнения по планимет- рии на готовых чертежах: [10], таблица № 4 |
|
Глава 2. Треугольники |
|
|
Модуль 2. Второй и третий признаки равенства треугольников |
|
|
Цели ученика: – овладение знанием основных понятий темы: равные треугольники, теорема-признак, соответственные элементы, углы, прилежащие к стороне, второй и третий признаки равенства треугольников; – освоение умения доказывать равенство треугольников с помощью второго и третьего признака равенства треугольников; – совершенствование умения пользоваться математической символикой при записи условия и доказательства теоремы, проводить доказательные рассуждения |
Цели педагога: – создание условий для формирования у учащихся представлений о понятии «теорема», «теорема-признак»; – организация познавательной деятельности на уроках с целью овладения алгоритмом выявления равных треугольников с помощью второго и третьего признаков равенства треугольников; – разработка заданий, позволяющих организовать деятельность учащихся по овладению общими приемами доказательства теорем (умением выделять в теореме условие и заключение), умением проводить доказательные рассуждения |
|
Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://mega.km.ru; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 2 (в рамках ЦДО) |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое обеспечение
педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
19 |
Второй признак равенства треугольников (изучение нового материала) |
[1], п. 19, вопрос 14 к |
Регулятивные: различать способ и результат действия. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: соответственные элементы, второй признак равенства треугольников (репродуктивно-алгоритмическое); – перевода текста (формулировки) второго признака равенства треугольников в графический образ, короткой записи, доказательства, применения для решения задач на выявление равных треугольников (продуктивно-комбинаторное). Умение:переводить текстовую информацию в графический образ и математическую модель, представлять информацию в сжатом виде – схематичной записи формулировки теоремы, проводить доказательные рассуждения, понимать специфику математического языка. Приобретенная компетентность: предметная |
Компетентностно-ориентированная. Исследовательская |
Теоретическое исследование |
Учебно-познавательная |
Фронтальная, индивидуальная |
Таблица «Признаки равенства треугольников» |
|
20 |
Второй признак равенства треугольников (комбинированный) |
Развивающее образование. Поисковая |
Проблемные задачи |
Познавательная, информационно-коммуникационная |
Групповая |
[8] § 9. [2] |
|||
|
21 |
Третий признак равенства треугольников (изучение нового материала) |
[1], п. 20, вопрос 15 к |
Регулятивные:различать способ и результат действия. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: соответственные элементы, третий признак равенства треугольников (репродуктивно-алгоритмическое); – перевода текста (формулировки) третьего признака равенства треугольников в графический образ, короткой записи, доказательства, применения для решения задач на выявление равных треугольников (продуктивно-комбинаторное). Умение: переводить текстовую информацию в графический образ и математическую модель, решать комбинированные задачи с использованием 1–2 алгоритмов, запи-сывать решения с помощью принятых условных обозна-чений. Приобретенная компетентность: предметная |
Компетентностно-ориентированная. Исследовательская |
Теоретическое исследование |
Учебно-познавательная |
Фронтальная, индивидуальная |
Таблица «Признаки равенства треугольников» |
|
22 |
Третий признак равенства треугольников (комбинированный) |
Развивающее образование. Поисковая |
Проблемные задачи |
Познавательная, информационно-коммуникационная |
Групповая |
[8] § 9. [2] |
|||
|
23 |
Решение задач на все признаки равенства
треугольников |
[1], п. 15, 19, 20; подготовка по вопросам к зачету |
Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок. Познавательные: проводить сравнение и классификацию по заданным критериям. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве |
Знание: – основных понятий темы: – перевода текста (формулировки) первого, второго, третьего признаков равенства треугольников в графический образ, короткой записи, доказательства, применения для решения задач на выявление равных треугольников (продуктивно-комбинаторное). Умение: переводить текстовую информацию в графический образ и математическую модель, решать задачи с использованием комбинирования 1–2 алгоритмов, записывать решения с помощью принятых условных обозначений. Приобретенная компетентность: предметная
|
Традиционно-педагогическая. Поисковая |
Практикум |
Учебно-познавательная |
Групповая |
[9] |
|
24 |
Зачет по теме «Признаки равенства треугольников» (контроль и оценка знаний) |
Контрольно-оценочная. Поисковая |
Проблемные задачи |
Рефлексивная |
Индивидуальная |
Дифференцированные карточки: [4],[8] |
|
Глава 2. Треугольники |
|
|
Модуль 3. Решение задач на построение |
|
|
Цели ученика: – определение содержания ключевого понятия «задача на построение», алгоритма построения биссектрисы угла, середины отрезка, перпендикуляра к прямой, угла, равного данному, с помощью циркуля и линейки; – овладение практическими навыками пользования геометрическими инструментами для построения заданных объектов, следуя пунктам инструкции (алгоритму), умением записать последовательность построений (последовательность собственных действий) |
Цели педагога: – создание условий для формирования у учащихся представлений о задачах на построение, алгоритмах построения биссектрисы угла, середины отрезка, перпендикуляра к прямой, угла, равного данному, с помощью циркуля и линейки; – организация познавательной деятельности на уроках с целью овладения практическими навыками пользования геометрическими инструментами для построения заданных объектов (учебно-познавательная компетентность) |
|
Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://mega.km.ru; http://www.rubricon.ru; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 13 (в рамках ЦДО) |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
25 |
Окружность (комбинированный) |
[1], п. 21, вопросы 16– |
Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Познавательные: ориентироваться
на разнообразие способов решения Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве |
Знание: – основных понятий темы: окружность, центр окружности, радиус, диаметр, хорда, дуга окружности (репродуктивно-алгоритмическое); – построения с помощью циркуля окружности заданного радиуса, элементов окружности, называния их с помощью принятых условных обозначений (продуктивно-комби- наторное); – подготовки презентации «Окружности
вокруг нас» Умение: – переводить текстовую информацию в
графический образ и математическую – составлять конспект математического текста, выделять главное, формулировать определения по описанию математических объектов. Приобретенная компетентность: учебно-познавательная, информационная |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Работа с текстом учебника |
Учебно-познавательная |
Фронтальная, индивидуальная |
Демонстрационный циркуль, линейка |
|
26 |
Построение циркулем и линейкой (комбинированный) |
Традиционно-педагогическая. Объяснительно-ил- люстративная |
Беседа, демонстрация |
Познавательная, информационно-коммуникационная |
[2] |
||||
|
27 |
Задачи |
[1], п. 22, 23, вопросы 19–21 к гл. II |
Регулятивные: различать способ и результат действия. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – определения содержания ключевого
понятия «задача на построение», способов решения задач на построение ческое); – построения с помощью чертежной линейки и циркуля угла, равного данному, биссектрисы угла, середины отрезка, называния их с помощью принятых условных обозначений (продуктивно-комбинаторное); – подбора информации кмини-проекту «Построения на песке, или как построить пирамиду» (продуктивно-креативное). Умение: выполнять алгоритмические предписания и инструкции (на примере построения биссектрисы, перпендикуляра, середины отрезка), овладевать азами графической культуры. Приобретенная компетентность: предметная, учебно-познавательная |
Развивающее образование. Поисковая |
Лабораторно-графическая |
Учебно-познавательная |
Фронтальная, индивидуальная |
[4] § 9, рабочие листы кой работе |
|
28 |
Задачи |
Развивающее образование. Поисковая |
Лабораторно-графическая |
Учебно-познавательная |
Фронтальная, индивидуальная |
[8] § 9 |
|||
|
29 |
Решение
задач ствование знаний) |
[1], п.
21– к гл. II |
Регулятивные: Познавательные:
владеть
общим приемом решения задач; ориентироваться на разнообразие способов
решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов; контролировать дей-ствия партнера |
Знание: – алгоритмов ключевых задач по всей теме, в том числе и на построение (репродуктивно-алгоритмическое); – способов решения задачи на определение вида треугольника, вычисления неизвестных элементов треугольника, записи решения с помощью принятых условных обозначений (продуктивно-комбинаторное); –
презентациимини-проекта «Построения на песке, или как построить пирамиду» Умение: переводить текстовую информацию в графический образ и математическую модель, решать комбинированные задачи с использованием 1–2 алгоритмов, запи-сывать решения с помощью принятых условных обозна-чений. Приобретенная компетентность: предметная |
Традиционно-педагогическая. Частично-поисковая |
Практикум |
Познавательная, информационно-коммуникационная |
Групповая |
[9] |
|
30 |
Контрольная работа по теме «Признаки равенства треугольников» (контроль и оценка знаний) |
Контрольно-оценочная. Поисковая |
Самостоятельное планирование и проведение решения |
Рефлексивная |
Индивидуальная |
[8], контрольная работа № 2. Дифференцированный раздаточный материал: [7], [11] |
|
Глава 3. Параллельные прямые (12 часов) |
|
|
Модуль 1. Признаки параллельности прямых |
|
|
Цели ученика: – овладение умением читать, записывать (в схематичном виде) признаки параллельности двух прямых; – освоение способов выявления параллельных прямых среди данных, умения доказывать свои предположения по поводу параллельности прямых с помощью изученных теорем-признаков; – совершенствование умения использовать математическую символику при записи решения задач на доказательство параллельности прямых |
Цели педагога: – создание условий для формирования у учащихся представлений о параллельности прямых; – организация познавательной деятельности по развитию умений различать факт, гипотезу, проводить доказательные рассуждения в ходе решения исследовательских задач по выявлению признаков параллельности двух прямых и способов их доказательства; – разработка практических заданий, позволяющих формировать у учащихся понимание специфики математического языка и навыки работы с математической символикой |
|
Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://www.uic.ssu.samara.ru/~nauka; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 15 (в рамках ЦДО) |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
31 |
Параллельные прямые (комбинированный) |
[1], п. 24– к гл. III |
Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: – накрест лежащих, односторонних, соответственных углов, перевода текста (формулировки) признаков параллельности в графический образ (продуктивно-комбинаторное). Умение: – передавать содержание прослушанного
материала – структурировать материал, понимать специфику математического языка и работы с математической символикой. Приобретенная компетентность: предметная, целостная |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Лекция, демонстрация |
Учебно-познавательная |
Учебно-познавательная |
Таблица «Признаки |
|
32 |
Признаки параллельности двух прямых (изучение нового материала) |
Развивающее образование. Поисковая |
Проблемное изложение |
Учебно-познавательная |
Фронтальная, индивидуальная |
Упражнения по планимет- |
|||
|
33 |
Признаки параллельности двух прямых (комбинированный) |
[1], п. 25, вопросы 4–6 |
Регулятивные: различать способ и результат действия. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: параллельные прямые, секущая, названия углов, образованных при пересечении двух прямых секущей (репродуктивно-алгоритмическое); – накрест лежащих, односторонних, соответственных углов, параллельности прямых на основе признаков параллельности, записи решения с помощью принятых обозначений (продуктивно-комбинаторное). Умение: – работать с готовыми предметными, знаковыми и графическими моделями для описания свойств и качеств изучаемых объектов; – проводить классификацию объектов (параллельные, непараллельные прямые) по заданным признакам. Приобретенная компетентность: предметная, целостная |
Развивающее образование. Поисковая |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая |
[8] § 13. [2] |
|
34 |
Признаки параллельности двух прямых (применение и совершенствование знаний) |
Развивающее образование. Поисковая |
Познавательная, информационно-коммуникационная |
Групповая |
[9] |
||||
|
35 |
Практические способы постро- ения параллельных прямых (комбинированный) |
[1], п. 25– к гл. III |
Регулятивные: шения. Познавательные: использовать
поиск необходимой информации для выполнения учебных заданий Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве |
Знание: – общего способа действий по построению параллельных прямых (репродуктивно-алгоритмическое); – построения параллельных прямых по выработанному алгоритму, записи выполняемых действий с помощью принятых обозначений, доказательства параллельности построенных прямых (продуктивно-комбинаторное). Умение:использовать соответствующие инструменты для решения практических задач, точно выполнять инструкции. Приобретенная компетентность: предметная |
Развивающее образование. Поисковая |
Беседа, демонстрация, графическая |
Познавательная, информационно-коммуникационная |
Фронтальная, парная (взаимопроверка) |
Демонстрационный чертежный треугольник, раздаточный материал для графической работы, цветные ручки для взаимопроверки |
|
36 |
Зачет по теме «Признаки параллельности двух прямых» (контроль и оценка знаний) |
Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок. Познавательные: строить
Коммуникативные: контролировать действия партнера |
Знание: – признаков параллельности прямых и их
доказательства – построения параллельных прямых, способов решения задач по теме (продуктивно-комбинаторное). Умение: распределить свою работу, оценить уровень владения материалом. Приобретенная компетентность: целостная |
Контрольно-оценочная. Поисковая |
Выполнение зачетных заданий |
Рефлексивная |
Индивидуальная |
Карточки |
|
Глава 3. Параллельные прямые |
|
|
Модуль 2. Аксиома параллельных прямых |
|
|
Цели ученика: – овладение умением определять содержание ключевого понятия «теорема, обратная к данной»; – освоение умения находить неизвестные углы, образованные двумя параллельными прямыми и секущей; – осваивание умений различать факт, гипотезу, развивать способность проводить доказательные рассуждения |
Цели педагога: – организация познавательной деятельности по решению поисковых задач на основе изученных теорем; – создание условий для формирования у учащихся представлений о понятии «теорема, обратная к данной» на примере теорем об углах, образованных двумя параллельными прямыми и секущей; – разработка заданий, позволяющих организовать деятельность учащихся по развитию умения различать факт, гипотезу, проводить доказательство в ходе изучения теорем по данной теме |
|
Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://mega.km.ru; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тесты № 16, 17 (в рамках ЦДО) |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
37 |
Аксиома параллельных прямых |
[1], п. 27– к гл. III |
Регулятивные: различать способ и результат действия. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – содержания ключевых понятий: аксиома, аксиоматический подход в геометрии, теорема, обратная к данной, теорема-следствие (репродуктивно-алгоритмическое); – формулировки аксиомы параллельных прямых, следствий из аксиомы параллельных прямых, определения параллельности прямых на основе нового признака параллельности, записи решения с помощью принятых обозначений (продуктивно-комбинаторное). Умение: работать с готовыми графическими моделями для описания свойств и качеств изучаемых объектов, проводить классификацию объектов (углов, полученных при пересечении двух прямых) по заданным признакам. Приобретенная компетентность: предметная, целостная |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Работа с текстом учебника |
Учебно-познавательная |
Фронтальная, индивидуальная |
Портреты ученых (Евклид, Лобачевский) |
|
38 |
Теоремы об углах, образованных двумя параллельными прямыми и секущей (комбинированный) |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Практикум |
Учебно-познавательная |
Фронтальная, индивидуальная |
[2]. [8] § 14. Таблица «Углы, образованные двумя параллельными прямыми и секущей» |
|||
|
39 |
Теоремы об углах, образованных двумя
параллельными прямыми и секущей |
[1], п. 29, вопросы 11–15 к гл. III |
Регулятивные: вносить необходимые коррективы в действие после его завершения на основе его и учета характера сделанных ошибок. Познавательные: строить
Коммуникативные: контролировать действия партнера |
Знание: – основных понятий темы: – способов решения задач на вычисление углов, образованных двумя параллельными прямыми и секущей, записи решения с помощью принятых обозначений (продуктивно-комбинаторное). Умение: переводить текстовую информацию в графический образ и математическую модель, представлять информацию в сжатом виде – схематичная запись формулировки теоремы, проводить доказательные рассуждения, понимать специфику математического языка. Приобретенная компетентность: предметная |
Компетентностно-ориентированная. Исследовательская |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая |
Упражнения по планимет- рии на готовых чертежах: [10], таблица № 7 |
|
40 |
Теоремы об углах, образованных двумя параллельными прямыми и секущей (комбинированный) |
Компетентностно-ориентированная. Исследовательская |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая |
[8] § 15, 16 |
|||
|
41 |
Теоремы об углах, образованных двумя параллельными пря- мыми |
[1], п. 24–29. Повторение всей |
Регулятивные: Познавательные: строить речевое высказывание в устной и письменной форме. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: – способов решения задач Умение: объяснять
изученные положения на самостоятельно подобранных примерах, проводить
классификацию (на примере видов углов при двух параллельных и секущей) по
выделенным признакам, доказательные Приобретенная компетентность: предметная, целостная |
Фронтальная. Индивидуальная |
Специально организованное общение |
Учебно-познавательная |
Фронтальная, индивидуальная |
[2] |
|
42 |
Контрольная работа по теме
«Параллельность |
Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок. Познавательные: строить
Коммуникативные: контролировать действия партнера |
Контрольно-оценочная. Поисковая |
Разноуровневые задания |
Рефлексивная |
Индивидуальная |
[8], контрольная работа № 3. Дифференцированный |
|
Глава 4. Соотношения между сторонами и углами треугольника (18 часов) |
|
|
Модуль 1. Соотношение между сторонами и углами треугольника |
|
|
Цели ученика: – формирование представлений о соотношении между сторонами и углами треугольника; – овладение умением различать факт, гипотезу, проводить доказательные рассуждения в ходе решения исследовательских задач на выявление соотношений сторон и углов в треугольнике |
Цели учителя: – создание условий для формирования у учащихся представлений о соотношении между сторонами и углами треугольника; – организация познавательной деятельности по развитию умения различать факт, гипотезу, проводить доказательные рассуждения в ходе решения исследовательских задач на выявление соотношений сторон и углов в треугольнике; – усвоения навыков доказательства соотношений сторон и углов в треугольнике; – формирования умений применять полученные знания в учебной деятельности |
|
Внеурочная деятельность:
поиск информации с использованием интернет-ресурсов: http://mega.km.ru;
http://www.rubricon.ru; |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
43 |
Сумма углов треугольника (изучение нового материала) |
[1], п. 30– к гл. IV |
Регулятивные: Познавательные: ориентироваться
на разнообразие способов решения Коммуникативные: учитывать
разные мнения и стремиться |
Знание: – содержания ключевых понятий: внутренний угол треугольника, внешний угол треугольника, сумма углов треугольника (репродуктивно-алгоритмическое); – теорем о сумме углов треугольника и
свойстве внешнего угла треугольника, способов их доказательства, алгоритмов
решения задач на нахождение углов треугольника, записи решения с помощью
принятых обозначений Умение: проводить
исследования несложных ситуаций Приобретенная компетентность: целостная, учебно-познавательная |
Компетентностно-ориентированная. Исследовательская |
Теоретическое исследование |
Познавательная, информационно-коммуникационная |
Групповая |
[8] § 17. Наборы треугольников, транспортир, рабочие листы с заданием для работы группы |
|
44 |
Сумма углов треугольника (изучение нового материала) |
Компетентностно-ориентированная. Исследовательская |
Теоретическое исследование |
Познавательная, информационно-коммуникационная |
Групповая |
Упражнения по планимет- рии на готовых чертежах: [10], таблица № 8, 9 |
|||
|
45 |
Соотношение между сторонами и углами треугольника (комбинированный) |
[1], п. 32, вопросы 6–11 к гл. IV |
Регулятивные: различать способ и результат действия. Познавательные: проводить
сравнение, сериацию и классификацию Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов
|
Знание: – содержания ключевых понятий: угол, противолежащий стороне, неравенство треугольников (репродуктивно-алгоритмическое); – теорем о соотношении между сторонами и углами треугольника, их доказательства и способов применения в решении задач, записи решения с помощью принятых обозначений (продуктивно-комбинаторное). Умение: – составлять конспект математического текста, выделять главное, формулировать определения по описанию математических объектов; – осуществлять перевод понятий из печатного (текст) в графический образ (чертеж). Приобретенная компетентность: учебно-познавательная, информационная |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Работа |
Учебно-познавательная |
Фронтальная, индивидуальная |
[2]. [8] § 18, 19 |
|
46 |
Соотношение между сторонами и углами треугольника (комбинированный) |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Практикум |
Учебно-познавательная |
Фронтальная, индивидуальная |
[9] |
|||
|
47 |
Соотношение между сторонами и углами треугольника (обобщающий) |
[1], п. 33– к гл. IV |
Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Познавательные: строить
Коммуникативные: контролировать действия партнера |
Знание: – содержания ключевых понятий: внутренний угол треугольника, внешний угол треугольника, сумма углов треугольника, неравенство треугольников (репродуктивно-алгоритмическое); – теорем о сумме углов треугольника и
свойстве внешнего угла треугольника, способов их доказательства, алгоритмов
решения задач на нахождение углов треугольника, записи решения с помощью
принятых обозначений Умение:приводить примеры, подбирать аргументы, вступать в речевое общение, участвовать в коллективной деятельности, оценивать работы других. Приобретенная компетентность: целостная, учебно-познавательная |
Развивающее образование. Поисковая |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая |
[2] |
|
48 |
Контрольная работа по теме «Сумма углов
треугольника» |
Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве |
Контрольно-оценочная. Поисковая |
Разноуровневые задания |
Рефлексивная |
Индивидуальная |
Дифференцированный раздаточный материал: [7], [11] |
|
Глава 4. Соотношения между сторонами и углами треугольника |
|
|
Модуль 2. Прямоугольные треугольники |
|
|
Цели ученика: – формирование представлений о признаках равенства прямоугольных треугольников; – овладение общими приемами решения поисковых задач; – совершенствование умения использовать для познания окружающего мира различные методы (наблюдение, измерение, моделирование), работать с полученной моделью |
Цели педагога: – создание условий для формирования у учащихся представлений о признаках равенства прямоугольных треугольников; – организация познавательной деятельности по решению поисковых задач на основе изученных теорем; – разработка заданий, позволяющих совершенствовать умение использовать для познания окружающего мира различные методы (наблюдение, измерение, моделирование) и умение работать с полученной моделью |
|
Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://www.uic.ssu.samara.ru/~nauka; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тесты № 19, 20, 22 (в рамках ЦДО) |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
49 |
Прямоугольные треугольники (комбинированный) |
[1], п. 35, вопросы 9–11 к гл. IV |
Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок. Познавательные: использовать
поиск необходимой информации для выполнения учебных заданий Коммуникативные: контролировать действия партнера |
Знание: – основных понятий темы: прямоугольный
треугольник, катет, гипотенуза, свойство острых углов треугольника, свойство
прямоугольного – доказательств свойств прямоугольного треугольника, применения их при решении поисковых задач (продуктивно-комбинаторное). Умение: различать факт, гипотезу, проводить доказательные рассуждения в ходе решения исследовательских задач на выявление соотношений углов прямоугольного треугольника. Приобретенная компетентность: предметная, целостная |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Специально организованное общение |
Учебно-познавательная |
Фронтальная, индивидуальная |
Таблица «Свойства прямоуголь-ного треугольника» |
|
50 |
Прямоугольные треугольники (комбинированный) |
Развивающее образование. Поисковая |
Проблемные задания |
Учебно-познавательная |
Фронтальная, индивидуальная |
[2]. [8] § 13 |
|||
|
51 |
Прямоугольные треугольники (применение и совершенствование знаний) |
[1], п. 35, 36, вопросы 12–13 к гл. IV |
Регулятивные: различать способ и результат действия. Познавательные: проводить сравнение, классификацию по заданным критериям. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: прямоугольный треугольник, катет, гипотенуза, признаки равенства прямоугольных треугольников (репродуктивно-алгоритмическое); – доказательств признаков равенства прямоугольных треугольников, способов решения задач на доказательство равенства прямоугольных треугольников, записи доказательства с помощью специальной символики (продуктивно-комбинаторное). Умение: проводить
исследования несложных ситуаций Приобретенная компетентность: целостная, предметная, учебно-познавательная |
Развивающее образование. Поисковая |
Теоретическое исследование |
Познавательная, информационно-коммуникационная |
Групповая |
Таблица «Признаки равенства прямоугольных треугольников» |
|
52 |
Прямоугольные треугольники (применение и совершенствование знаний) |
Развивающее образование. Поисковая |
Проблемные задания |
Познавательная, информационно-коммуникационная |
Групповая |
[9] |
|||
|
53 |
Решение задач ствование знаний) |
[1], п. 34– к гл. IV |
Регулятивные:
вносить необходимые коррективы в действие после его завершения на основе
учета характера сделанных ошибок; оценивать правильность выполнения действия Познавательные: владеть
общим приемом решения Коммуникативные: договариваться
и приходить к общему решению в со-вместной деятельности, |
Знание: – основных понятий темы: прямоугольный треугольник, катет, гипотенуза, признаки равенства прямоугольных треугольников (репродуктивно-алгоритмическое); – доказательств признаков равенства прямоугольных треугольников, способов решения задач на доказательство равенства прямоугольных треугольников, записи доказательства с помощью специальной символики (продуктивно-комбинаторное). Умение: переводить текстовую информацию в графический образ и математическую модель, решать комбинированные задачи с использованием 2–3 алгоритмов, проводить доказательные рассуждения в ходе презентации решения задач, составлять обобщающие таблицы. Приобретенная компетентность: предметная |
Компетентностно-ориентированная. Исследовательская |
Организация совместной учебной деятельности |
Учебно-познавательная |
Групповая (группы сменного состава) |
Дифференцированный раздаточный материал |
|
54 |
Решение задач ствование знаний) |
Компетентностно-ориентированная. Исследовательская |
Организация совместной учебной деятельности |
Учебно-познавательная |
Групповая (группы сменного состава) |
Дифференцированный раздаточный материал |
|
Глава 4. Соотношения между сторонами и углами треугольника |
|
|
Модуль 3. Построение треугольника по трем элементам |
|
|
Цели ученика: – формирование представлений о способах построения треугольников по трем заданным элементам; – овладение общими приемами решения задач на построение; – освоение практических навыков пользования геометрическими инструментами для построения заданных объектов, следуя пунктам инструкции (алгоритму), умения записывать последовательность построений (последовательность собственных действий) |
Цели педагога: – создание условий для формирования у учащихся представлений о способах построения треугольников по трем заданным элементам; – организация познавательной деятельности по овладению общими приемами решения задач на построение, практическими навыками пользования геометрическими инструментами для построения заданных объектов, следуя пунктам инструкции (алгоритму), умением записывать последовательность построений (последовательность собственных действий) |
|
Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://mega.km.ru; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 21 (в рамках ЦДО) |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
55 |
Расстояние от точки до прямой (комбинированный) |
[1], п. 38, вопросы 16–18 к гл. IV |
Регулятивные: различать способ и результат действия. Познавательные: проводить сравнение, классификацию по заданным критериям. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: перпендикуляр, расстояние от данной точки до прямой, расстояние между параллельными прямыми (репродуктивно-алгоритмическое); – способов действия по нахождению (построению) расстояния от точки до прямой и между параллельными прямыми, записи решения с помощью принятых условных обозначений (продуктивно-комбинаторное). Умение: – составлять конспект математического текста, выделять главное, формулировать определения по описанию математических объектов; – осуществлять перевод понятий из текстовой формы в графическую. Приобретенная компетентность: учебно-познава- |
Традиционно-педагогическая. Объяснительно-иллюстративная |
Работа |
Учебно-познавательная |
Фронтальная, индивидуальная |
Демонстрационный чертежный угольник |
|
56 |
Расстояние между параллельными прямыми (комбинированный) |
Традиционно-педагогическая. Частично- поисковая |
Проблемные задания |
Учебно-познавательная |
Фронтальная, индивидуальная |
[8] § 22. [9] |
|||
|
57 |
Построе- ние треугольника по трем элементам (комбинированный) |
[1], п. 39, вопросы 19–20, к гл. IV |
Коммуникативные: учитывать
разные мнения и стремиться |
Знание: – основных понятий темы: треугольник, равный данному, признаки равенства треугольников, задача на построение (репродуктивно-алгоритмическое); – построения с помощью циркуля и линейки треугольника по трем заданным элементам, называния их с помощью принятых условных обозначений, доказательства, что построен треугольник, равный заданному (продуктивно-комбинаторное). Умение: грамотно
выполнять алгоритмические пред-писания и инструкции Приобретенная компетентность: предметная, учебно-познавательная |
Развивающее образование. Поисковая |
Лабораторно-графическая |
Учебно-познавательная |
Фронтальная, индивидуальная |
[8] § 24, 25 |
|
58 |
Построе- ние треугольника по трем элементам (применение
и совершенствование |
Развивающее образование. Поисковая |
Лабораторно-графическая |
Учебно-познавательная |
Фронтальная, индивидуальная |
[2] |
|||
|
59 |
Решение задач (применение и совершенствование знаний) |
|
Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Познавательные: использовать
поиск необходимой информации для выполнения учебных заданий |
Знание: – основных понятий темы: сумма углов
треугольника, свойство внешнего угла – способов решения поисковых задач на соотношение сторон и углов в треугольнике, на построение треугольников (продуктивно-комби- наторное). Умение: переводить текстовую информацию в графический образ и математическую модель, решать комбинированные задачи с использованием 2–3 алгоритмов, проводить доказательные рассуждения в ходе презентации решения задач, составлять обобщающие таблицы. Приобретенная компетентность: предметная |
Компетентностно-ориентированная. Исследовательская |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая (группы сменного состава) |
[9] |
|
60 |
Контрольная работа по теме «Соотношение между сторонами и углами треугольника» (контроль и оценка знаний) |
Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок. Познавательные: строить
Коммуникативные: контролировать действия партнера |
Контрольно-оценочная. Поисковая |
Самостоятельное планирование и проведение решения |
Рефлексивная |
Индивидуальная |
[8], контрольная работа № 4. Дифференцированный |
|
Обобщающее повторение (8 часов) |
|
|
Цели ученика: систематизация имеющихся представлений об изученных планиметрических фигурах, их признаках, свойствах и способах решения планиметрических задач |
Цели педагога: организация познавательной деятельности, позволяющей учащимся систематизировать имеющиеся у них представления об изученных планиметрических фигурах, их признаках, свойствах и способах решения планиметрических задач |
|
Внеурочная деятельность: самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тесты № 1–21 (в рамках ЦДО) |
|
|
№ |
Тема |
Самостоятельная работа |
Универсальные учебные действия (УУД) |
Планируемые предметные |
Вид педагогической |
Педагогические средства |
Ведущая деятельность, осваиваемая в системе занятости |
Формы организации совзаимодействия на уроке |
Информационно-методическое
обеспечение педагогической системы урочной |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
61 |
Простейшие фигуры планиметрии: прямая, луч, угол (обобщение и систематизация знаний) |
[1], п. 1–13, вопросы к гл. I |
Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: прямая, луч, перпендикулярные прямые, градусная мера угла, острые, тупые, прямые, развернутые, смежные, вертикальные углы (репродуктивно-алгоритмическое); – построения с помощью чертежной линейки углов, измерения их величины с помощью транспортира, записи измерений с помощью принятых условных обозначений, построения углов заданной величины, определения вида угла, применения свойств смежных и вертикальных углов (продуктивно-комбина- торное). Умение: проводить
исследования несложных ситуаций Приобретенная компетентность: целостная, предметная, учебно-познавательная |
Компетентностно-ориентированная. Исследовательская |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая |
[8]. Итоговое повторение |
|
62 |
Простейшие фигуры планиметрии: прямая, луч, угол (обобщение и систематизация |
Компетентностно-ориентированная. Исследовательская |
Познавательная, информационно-коммуникационная |
Групповая |
[8] § 26, варианты 1–2 |
||||
|
63 |
Треугольники |
[1], п. 14– к гл. II |
Регулятивные: различать способ и результат действия. Познавательные: проводить сравнение, классификацию по заданным критериям. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: треугольник
равнобедренный, прямоугольный, равносторонний треугольник, первый, второй,
третий признаки равенства треугольников – применения признаков равенства треугольников для выявления равных треугольников, определения вида данного треугольника, способов решений задач на сумму углов треугольника (продуктивно-комбинаторное). Умение:переводить текстовую информацию в графический образ и математическую модель, решать комбинированные задачи с использованием 1–2 алгоритмов, запи-сывать решения с помощью принятых условных обозна-чений. Приобретенная компетентность: предметная |
Компетентностно-ориентированная. Исследовательская |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая |
Таблица «Признаки равенства треугольников» [8] § 26, варианты 3–5 |
|
64 |
Треугольники (обобщение и систематизация |
Компетентностно-ориентированная. Исследовательская |
Познавательная, информационно-коммуникационная |
Групповая |
[8]. Итоговое повторение |
||||
|
65 |
Параллельные прямые (обобщение и систематизация |
[1], п. 24– к гл. III |
Регулятивные: различать способ и результат действия. Познавательные: проводить сравнение, классификацию по заданным критериям. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Знание: – основных понятий темы: – накрест лежащих, односторонних, соответственных углов, определения парал-лельности прямых на основе признаков параллельности, записи способов решения с помощью принятых обозначений (продуктивно-комбинаторное). Умение: работать с готовыми предметными, знаковыми и графическими моделями для описания свойств и качеств изучаемых объектов, проводить классификацию объектов (параллельные, непараллельные прямые) по заданным признакам. Приобретенная компетентность: учебно-познава- |
Компетентностно-ориентированная. Исследовательская |
Организация совместной учебной деятельности |
Познавательная, информационно-коммуникационная |
Групповая |
[8] Итоговое повторение |
|
66 |
Параллельные прямые (обобщение и систематизация |
Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Познавательные: владеть
общим приемом решения Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов |
Групповая |
[8] Итоговое повторение |
|||||
|
67– |
Итоговая контрольная работа (контроль и оценка знаний) |
[1], п. 24– к гл. III |
Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве |
Знание: – основных понятий курса геометрии 7 класса (репродуктивно-алгоритмическое); – способов решения поисковых задач по всему курсу, записи решения с помощью принятых обозначений (продуктивно-комбинаторное). Умение: владеть навыками распределения своей работы, оценивать уровень владения материалом |
Контрольно-оценочная. Поисковая |
Самостоятельное планирование и проведение решения |
Рефлексивная |
Индивидуальная |
[8] Итоговая контрольная работа |
Скачано с www.znanio.ru
© ООО «Знанио»
С вами с 2009 года.
![]()