
РЕЙТЕР КИРИЛЛ АЛЕКСАНДРОВИЧ
к.ф.н., доцент, ЗДН АЕ, член-кор. Академии Естествознания
«ТЕРМОДИНАМИКА, ТЕПЛОПЕРЕДАЧА И ГИДРАВЛИКА»
УЧЕБНИК
для программы подготовки специалистов среднего звена по специальностям:
20.02.04 Пожарная безопасность
20.02.02 Защита в чрезвычайных ситуациях
Тема 1.1. Основы гидростатики
Тема 1.2. Основы гидродинамики
Тема 1.3. Движение реальных жидкостей
Тема 1.4. Истечение жидкостей
Тема 1.5. Трубопроводы
Тема 2.1. Основы термодинамики
Тема 2.2. Законы термодинамики
Тема 2.3. Идеальные газы
Тема 2.4. Термодинамические процессы и циклы
Тема 2.5. Термодинамика потоков
Тема 2.6. Термодинамический анализ теплотехнических устройств
Тема 3.1. Теплопроводность
Тема 3.2. Конвективный теплообмен Тема 3.3. Процессы теплопередачи
Раздел 1. Гидравлика
Тема 1.1. Основы гидростатики
Гидравликой называется прикладная наука, в которой изучаются законы движения и равновесия жидкости и даются способы приложения этих законов к решению конкретных технических задач.
Гидравлика – одна из самых древних наук в мире. Результаты археологических исследований показывают, что еще за 5000 лет до н.э. в Китае и других странах Древнего мира уже существовали оросительные каналы и были известны простейшие устройства для подъема воды. В Риме сохранились остатки древнего водопровода, построенного за шесть веков до начала нашей эры.
Гидравлика (греч. «хюдор» - вода и «аулос» - труба, канал, струя) – прикладная наука, изучающая законы равновесия и движения жидкости и разрабатывающая на основе теории и эксперимента способы применения этих законов к решению различных задач инженерной практики. Гидравлика – очень древняя наука. За несколько тысяч лет до нашей эры в Индии, Китае, в Египте, странах Ближнего и Среднего востока уже строились различные гидротехнические сооружения: каналы, платины, водяные колеса. Первым научным трудом в области гидравлики считается написанный примерно за 250 лет до н.э. трактат Архимеда «О плавающих телах», в котором величайший ученый древности сформулировал закон о давлении жидкости на погруженное в нее тело. Особое развитие гидравлика получила в средние века. В XV веке Леонардо да Винчи написал труд «О движении и измерении воды в тесных сооружениях», опубликованный через 307 лет после его смерти в 1826 году. В 1586 году голландский ученый Симон Стевин опубликовал работу «Начало гидростатики». В XVI – XVII веках Г. Галилей, Э. Таричелли, Б. Паскаль и И. Ньютон проводили исследования, позволившие разработать основы гидромеханики. В 1755 – 1756 годах выходят в свет работы Л.П. Эйлера, где впервые приводится полная система дифференциальных уравнений равновесия и движения идеальной ж. Основоположниками гидравлики как самостоятельной науки являются члены Петербургской академии наук М.В. Ломоносова, Д.И. Бернулли, Л.П. Эйлер. В 1738 году была опубликована работа Д. Бернулли «Гидравлика или записки о силах движения жидкости», в которой установлена зависимость между давлением и скоростью в элементарной струйке идеальной жидкости. Представляют интерес такие работы Шизе, Вентури, Вейсбаха, Дарси, Базена и Рейнольдса. Труды этих ученых посвящены главным образом изучению турбулентности потоков и установлению общих законов сопротивления движению вязких жидкостей, а также исследованию движения жидкости в трубах, каналах и на водосливах. Большое внимание уделено в них также разработке теории размерности и подобия и постановке лабораторных экспериментов.
В 1791 году вышла в свет первое русское руководство по гидравлике А. Колмакова «Карманная книжка для вычисления количества воды, вытекающей через трубы, отверстие или по желобам, также и силы, какой они ударяют, стремясь с данной скоростью».
Большой вклад в развитие гидравлики принесли советские ученые: А.Н. Колмогоров (теория турбулентности), Н.Н Павловский (теория фильтрации, равномерное и неравномерное движение жидкости), И.Н. Куколевский (теория машиностроительной гидравлики), С.А. Христианович (неустановившиеся движения жидкости) и многое другие.
Все вещества в природе имеют молекулярное строение. По характеру межмолекулярных связей жидкости занимают промежуточное положение между твердыми телами и газами. Свойства жидкостей при высоких температурах и низких давлениях ближе к свойствам газов, а при низких температурах и высоких давлениях – к свойствам твердых тел.
Гипотеза сплошности. Жидкость в целом рассматривают как сплошную среду, непрерывно заполняющую пространство, т.е. принимают, что в жидкости нет пустот или разрывов, что все характеристики жидкости являются непрерывными функциями, имеющими непрерывные частные производные по всем своим аргументам.
Рассмотрим следующие свойства и понятия:
• плотность
• удельный вес
• удельный объем
• сжимаемость (модуль упругости, скорость звука)
• температурное расширение
• вязкость (закон Ньютона, вискозиметр, текучесть)
• сопротивление растяжению
• поверхностное натяжение (капиллярность)
• растворимость газов в жидкостях (закон Генри, кавитация)
• понятие об идеальной жидкости
Замечание о системах единиц
Исторически сложилось так, что одновременно используются 3 системы единиц.
Международная система единиц измерения СИ (система интернациональная) – рекомендована к применению, однако учебники, инструкции и приборы не всегда ей соответствуют. СИ (метр, килограмм массы, секунда)
Физическая СГС (сантиметр, грамм, секунда)
Техническая МКГСС (метр, килограмм силы, секунда)
1. Плотность – масса единицы объема
Плотность характеризует
распределение массы жидкости m
по объему V .
В произвольной точке A
жидкости плотность A Vlim0 ![]() Vm ,
Vm ,
где m – масса, заключенная в объеме V , стягиваемом в точку A.
Плотность однородной жидкости равна отношению массы m жидкости к ее объему m кг
![]() V : V
V : V![]() . Единица измерения
м3 .
. Единица измерения
м3 .
Все жидкости кроме воды характеризуются уменьшением плотности при увеличении температуры. Плотность воды максимальна при 4С воды1000 кг/м3 и уменьшается как с уменьшением, так и с увеличением температуры. В этом проявляется одно из аномальных свойств воды. В гидравлических расчетах можно принимать плотность воды неизменной 1000 кг/м3.
2. ![]() Удельный вес – вес единицы
объема. g Запомнить: g
Удельный вес – вес единицы
объема. g Запомнить: g
Единица измерения в системе СИ н/м3 . воды 9810 н/м3.
В гидравлических расчетах можно принимать g=9.81 м/c2.
Точная константа для перевода единиц измерения 9,80665.
3. ![]() Удельный объем – объем
единицы массы V
1
Удельный объем – объем
единицы массы V
1
По определению величина обратная плотности; единица измерения м3/кг.
4. Сжимаемость – способность жидкости изменять объем при изменении давления.
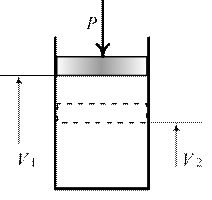
Рис. 1.1. Объемное сжатие
Характеризуется коэффициентом объемного сжатия p , Па-1, представляющим относительное изменение объема жидкости V при изменении давления p на единицу (при постоянной температуре).
dV
p ![]() . Знак «минус» в формуле указывает, что при увеличении давления
. Знак «минус» в формуле указывает, что при увеличении давления
V dp
объем жидкости уменьшается.
Величина обратная коэффициенту объемного сжатия – модуль (объемной) упругости
1
жидкости (не следует называть «жесткость», как в физике). E ![]() . Eводы2,1103
. Eводы2,1103
МПа, Eстали 2,1105 МПа.
Сжимаемость воды весьма незначительна. При увеличении давления на 100 кПа (примерно 1 кг/см2) объем воды уменьшится на 1 / 20 000. В гидравлических расчетах можно считать воду несжимаемой средой. Однако это справедливо лишь при небольших давлениях. Так, если бы вода в Мировом океане была абсолютно несжимаема, то уровень воды поднялся бы на 30 метров. Учитывать сжимаемость надо в гидравлических следящих приводах и в теории гидроудара.
В безграничной однородной жидкости или в объеме, ограниченном абсолютно жест-
E
![]() кими
стенками, скорость распространения звука c .
кими
стенками, скорость распространения звука c .
Для воды при 10С c=1425 м/с.
5. Температурное расширение – свойство жидкостей изменять объем при изменении температуры.
Характеризуется коэффициентом температурного расширения t , С –1, представляющим относительное изменение объема жидкости при изменении температуры на 1С (при постоянном давлении).
![]() dV (знак «плюс», т.к. при
увеличении температуры объем увеличивается).
dV (знак «плюс», т.к. при
увеличении температуры объем увеличивается).
t V dt
Величина t для воды меняется в зависимости от температуры. Из сказанного ранее следует, что для воды при 0С t =0. Удельный объем воды при различных температурах и давлениях могут быть посчитаны по специальным формулам и приводится в таблицах (см. Ривкин, Александров)
6. Вязкость – это свойство жидкости оказывать сопротивление относительному сдвигу ее слоев.
Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхности их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения или силами вязкости.
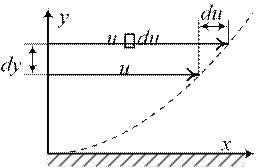
Рис. 1.2. График движения жидкости вдоль стенки
Рассмотрим движение жидкости вдоль стенки. Слой жидкости, непосредственно прилегающий к стенке, прилипает к ней. Существует разность скоростей между соседними слоями и возникает взаимное скольжение слоев, которое приводит к возникновению силы du
внутреннего трения.Сила трения T F . Касательное напряжение сдвига есть dy
сила, отнесенная к площади действия. По закону Ньютона для вязкого трения касательное напряжение du
, ЗАКОН НЬЮТОНА (закон внутреннего трения Ньютона) dy du
где ![]() – градиент
скорости в направлении, перпендикулярном движущимся слоям dy жидкости.
– градиент
скорости в направлении, перпендикулярном движущимся слоям dy жидкости.
Напомним: напряжение это сила, приходящаяся на единицу площади, следовательно силу вязкого трения T между слоями жидкости площадью F можно найти: du
T F F
dy
(Коэффициент пропорциональности есть динамический коэффициент вязкости жидкости (иногда называют абсолютной вязкостью в отличие от кинематического коэффициента вязкости, который отнесен к плотности). Знак в формуле выбирают в зависимости от направления оси и знака градиента скорости так, чтобы касательное напряжение было положительным (ибо отрицательным оно быть не может – всегда тормозит слой с большей скоростью).
Единица измерения динамического коэффициента вязкости в системе СИ Пас.
Единица «пуаз» (в память французского ученого Пуазейля, обозначается П) в 10 раз меньше, т.е. 1 Пас =10 П.
н кг м кг г
![]() Для
справки: Пас м2 с с2м2 с м с , П
Для
справки: Пас м2 с с2м2 с м с , П
![]() смс .
смс .
В гидравлических расчетах кроме динамической вязкости широко используют кинематический коэффициент вязкости (обозначается буквой – «ню», греч.), равную отношению динамической вязкости к плотности жидкости
![]()
м2
Единица измерения кинематической вязкости в системе СИ ![]() . с
. с
Единица «стокс» (в память английского ученого Стокса, обозначается Ст) равна см2/с, следовательно 1 м2/с=104 Ст. В справочниках используется «сантистокс», 100 сСт=1 Ст.
С повышением температуры кинематическая вязкость газов увеличивается, а вязкость капельных жидкостей уменьшается.
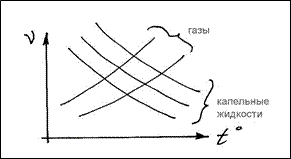
Рис 1.3. Иллюстрация увеличения кинематическая вязкости газов и уменьшения вязкость капельных жидкостей при увеличении температуры.
|
Для воды и воздуха , Ст |
С |
температура, |
Вода |
воздух |
|
|
0 С |
0,0179 |
0,133 |
|
|
|
20 С |
0,0101 |
0,151 |
Поэтому с целью уменьшения потерь при транспортировке вязкие жидкости, например мазут, нагревают, а воздуховоды и газопроводы охлаждают.
Для воды вязкость (до 60 С) 1![]() 0,0337t 0,000221t2 (Киселев, стр. 13)
0,0337t 0,000221t2 (Киселев, стр. 13)
Измерение вязкости производят с помощью приборов различных типов и конструкций, называемых вискозиметрами.
Вискозиметр Энглера. Термостат с сосудом объемом 200 см3 с отверстием в дне диаметром 3 мм. Вязкость измеряется в градусах Энглера (обозначается Е). Градусом Энглера называется отношение времени истечения 200 см3 исследуемой жидкости к времени истечения такого же объема дистиллированной воды (примерно 50с) при температуре 20С. Для перехода от вязкости жидкости, выраженной в градусах Энглера, к кинематическому коэффициенту вязкости можно пользоваться эмпирической формулой Фогеля
0,0731oE ![]() 0,o0631,
см2/с .
0,o0631,
см2/с .
E
С свойством вязкости связано свойство текучести.
Текучесть – способность существенно изменять форму под действием слабых внешних воздействий, в частности под действием силы тяжести.
Текучесть свойственна жидкостям и газам в которых частицы легкоподвижны и нет касательных напряжений между слоями в состоянии покоя. Численно текучесть – величина обратная вязкости.
7. Сопротивление растяжению жидкости не сопротивляются растягивающим напряжениям. При снижении давления до давления насыщенных паров жидкости при данной температуре в жидкости образуются пустоты, заполненные паром. Нарушается целостность жидкости. Если давление повысить, то пустоты исчезнут, пар снова перейдет в жидкость.
8. Поверхностное натяжение жидкости под действием внутренних сил стремится уменьшить свою поверхность, если ей в этом не препятствуют какие-либо силы. Коэффициент поверхностного натяжения («сигма», греч.) численно равен работе, которую нужно затратить для увеличения поверхности жидкости на единицу площади. Другое определение: коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность.
Для воды =0,074 н/м.
Из-за поверхностного натяжения давление в капле воды радиуса r больше давления в
окружающей
среде на величину p ![]() . На ту же величину больше давление в пузырьке r
. На ту же величину больше давление в пузырьке r
воздуха в толще жидкости.
Капиллярность – способность жидкости подниматься или опускаться под действием сил поверхностного натяжения в трубках малого диаметра.
 Жидкость может
смачивать поверхность твердого тела (вода – стекло) или не смачивать
(ртуть–стекло).
Жидкость может
смачивать поверхность твердого тела (вода – стекло) или не смачивать
(ртуть–стекло).
Внутренний диаметр трубок пьезометров не должен быть меньше 5 мм, чтобы не было искажения показаний.
9. Адгезия – способность молекул жидкости прилипать к поверхности твердого тела.
10. ![]() Растворимость газов в жидкостях подчиняется
закону Генри Vг
k p , при-
Растворимость газов в жидкостях подчиняется
закону Генри Vг
k p , при-
Vж po
чем k f (to) . Растворенный в воде при нормальных условиях воздух составляет 2% по объему. Коэффициент растворимости воды k=0,016 при Н.У. (101 кПа, 15С), для масла k=0,08.
Кавитация – процесс образования паро-воздушных пузырьков в области пониженного давления и их захлопывание в области повышенного давления.
Газ как сжимаемая жидкость
В газах расстояния между молекулами больше, а межмолекулярные силы меньше, чем в жидкостях и твердых телах, поэтому газы отличаются от жидкостей и твердых тел обладают большей сжимаемостью.
Плотность газов существенно зависит от температуры и давления и может быть определена с использованием закона Менделеева – Клапейрона
pv RT , где p – абсолютное давление; v – удельный объем газа; R
=287,1 Дж/кгК– универсальная газовая постоянная; T – абсолютная температура К p
(С+273,15).
Учитывая, что 1/v имеем: ![]() . RT
. RT
Жидкость и основные понятия гидравлики
Жидкость – тело, обладающее свойством текучести, т.е. способное сколь угодно сильно изменять свою форму под действием сколь угодно малых сил. В отличие от газа весьма мало изменяет свою плотность при изменении давления.
Жидкая частица – выбранный для рассмотрения бесконечно малый объем жидкости, сохраняющий все ее свойства.
Жидкая частица – часть жидкости, малая по сравнению с объемом рассматриваемой жидкости, и в то же время объем частицы велик по сравнению с объемом молекулы жидкости.
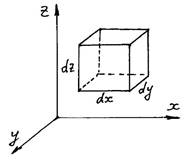 Обычно в жидкости
выделяют для рассмотрения прямоугольный параллелепипед («кубик») с ребрами dx,dy,dz , ориентированными по
координатным осям.
Обычно в жидкости
выделяют для рассмотрения прямоугольный параллелепипед («кубик») с ребрами dx,dy,dz , ориентированными по
координатным осям.
Тогда объем жидкой частицы («элементарный объем»)
dV dx dy dz , масса частицы
dm dV dx dy dz .
Эти очевидные соотношения в дальнейшем будут неоднократно использоваться без пояснений.
Идеальная жидкость – это воображаемая жидкость абсолютно несжимаемая и невязкая.
Невязкая – при движении не возникает касательных напряжений.
Реальная жидкость( «вязкая жидкость») – жидкость действительная, обладающая всеми характерными для нее физическими свойствами (обычно противопоставляется термину «идеальная жидкость»).
Капельная жидкость – образует капли, так как на поверхности раздела жидкости и газа действуют силы поверхностного натяжения.
В гидравлике рассматриваются только капельные жидкости, т.е. обладающие свойством текучести, но в отличие от газа крайне мало изменяющие свою плотность при изменении давления.
К покоящейся жидкости не могут быть приложены сосредоточенные силы, а только распределенные по объему(массовые) или по поверхности (поверхностные).
1. Массовые силы:
Плотность распределения массовой силы есть сила, отнесенная к массе.
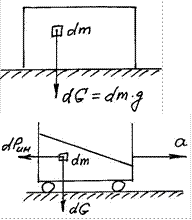 Сила тяжести
– обусловлена Земным притяжением На элементарную массу dm действует сила dG.
Сила тяжести
– обусловлена Земным притяжением На элементарную массу dm действует сила dG.
dG
Плотность распределения силы ![]()
g (ускорение
dm
g (ускорение
dm
свободного падения).
Сила инерции – обусловлена движением с ускорением a0. dPин dma .
![]() Плотность распределения
силы инерции dPин a
Плотность распределения
силы инерции dPин a
dm
(ускорение).
Направление скорости безразлично.
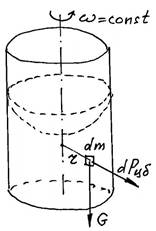 Центробежная сила
– обусловлена движением с ускорением при вращении. (фактически сила инерции)
Центробежная сила
– обусловлена движением с ускорением при вращении. (фактически сила инерции)
2
2 u
dPцб dm r dm ![]() , где –
угловая скорость
, где –
угловая скорость
r
вращения; r – радиус, на котором находится масса dm ; u – линейная скорость.
Плотность распределения центробежной силы
![]() dPцб 2
r (ускорение) dm
dPцб 2
r (ускорение) dm
Силы, действующие на каждый элемент поверхностей, ограничивающих жидкость, и на каждый элемент поверхностей, проведенных произвольно внутри жидкости, называют поверхностными.
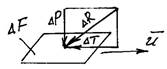 Сила dR, действующая на
площадку площадью F , представляется как сумма силы нормального
напряжения Pи силы касательного
напряжения T .
Сила dR, действующая на
площадку площадью F , представляется как сумма силы нормального
напряжения Pи силы касательного
напряжения T .
Плотность распределения поверхностной силы есть сила, отнесенная к площади действия.
Плотность распределения нормальных сил p ![]() называют нормальным напряжением
называют нормальным напряжением
(давлением). Плотность распределения касательных сил ![]() называют касательным
называют касательным
напряжением.
Массовые и поверхностные силы могут быть внешними и внутренними.
Внешние силы действуют на рассматриваемую массу и поверхность жидкости извне и приложены соответственно к каждой частице жидкости, составляющей массу, и к каждому элементу поверхности, ограничивающей жидкость. Внутренние силы представляют собой взаимодействие частиц жидкости. Они являются парными, их сумма в данном объеме жидкости всегда равна нулю.
Гидростатика – раздел гидравлики, изучающий законы равновесия жидкостей в состоянии покоя.
Абсолютный покой – все частицы жидкости неподвижны относительно Земли (в общем случае – относительно неинерциальной системы отсчета)
Относительный покой – частицы жидкости неподвижны по отношению к резервуару, который движется с ускорением относительно Земли.
P
Нормальное напряжение –
плотность распределения нормальных сил p ![]() .
.
F
 Это нормальное усилие
отнесенное к величине этой площади.
Это нормальное усилие
отнесенное к величине этой площади.
![]() P
P
F0 F
Нормальное напряжение – вектор.
Свойства нормального напряжения
1. Нормальное напряжение действует по внутренней нормали к пощади действия (является сжимающим напряжением).
Доказательство. Покажем, что сила P действует по внутренней нормали к площадке F . Доказательство от противного. а) Если бы сила была направлена не по нормали, то ее можно было бы разложить на нормальную и касательную составляющие. Из-за текучести жидкости касательная составляющая привела бы жидкость в движение, т.е. в этом случае равновесие жидкости было бы невозможно. Значит сила направлена по нормали. б) Так как жидкость не сопротивляется растягивающим напряжениям, то сила P может быть только сжимающей.
2. В покоящейся жидкости значение (модуль) нормального напряжения не зависит от ориентации площадки.
Доказательство.
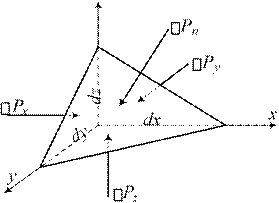 z Выделим
в покоящейся жидкости элементарную частицу в форме тетраэдра с ребрами x , y , z, выбранными вдоль
координатных осей. Площадь основания
z Выделим
в покоящейся жидкости элементарную частицу в форме тетраэдра с ребрами x , y , z, выбранными вдоль
координатных осей. Площадь основания ![]() xy , высота z, объем (одна треть
xy , высота z, объем (одна треть
площади основания на высоту)
1 V ![]() x y z .
x y z .
6
Отбросим окружающую тетраэдр жидкость и для сохранения равновесия приложим к каждой грани тетраэдра поверхностные силы Px , Py , Pz по направлениям осей и Pn
, действующую на наклонную грань по направлению нормали к ней n . Кроме поверхностных на жидкость, заключенную в тетраэдре, действует массовая сила, проекции плотности распределения которой на оси координат обозначим X , Y , Z .
Массовая сила равна произведению массы на плотность распределения силы. В направлении оси x действует массовая сила V X .
Уравнение равновесия жидкости, заключенной в тетраэдре (сумма сил равна нулю), в проекции на ось x :
Px V X Pn cos(n,x) , здесь (n, x) –угол между нормалью к наклонной грани и осью координат.
Разделим обе части уравнения на площадь грани, перпендикулярной оси x :
![]() Px V X
Pn cos(n,x)
Px V X
Pn cos(n,x)
Fx Fx Fx
Упростим, учитывая что Fx Fn cos(n.x) ![]() yz
yz
![]() Px
xX
Pn . Стягиваем
тетраэдр в точку, второе слагаемое обращается в 0,
Px
xX
Pn . Стягиваем
тетраэдр в точку, второе слагаемое обращается в 0,
Fx 3 Fn
имеем: px pn . Проекции уравнения равновесия на другие оси приведут к выводам: py pn и pz pn .
Следовательно px py pz pn . Таким образом доказано, что величина нормального напряжения в любой точке покоящейся жидкости не зависит от направления действия.
p2 p1 Это позволяет характеризовать напряженное состояние по-коящейся жидкости в каждой точке скалярной величиной,
 представляющей значение нормального напряжения в этой
представляющей значение нормального напряжения в этой
12 точке и называемой гидростатическое давление (в даль-
нейшем слово «гидростатическое» опускается).
Давление может быть неодинаковым в разных точках покоящейся жидкости:
p f (x, y,z) .
Единицы измерения давления:
p
![]() н2 =Па (Паскаль)
1 кПа=103Па; 1 МПа=106 Па; 1 бар=105 Па м
н2 =Па (Паскаль)
1 кПа=103Па; 1 МПа=106 Па; 1 бар=105 Па м
2
см
Единицы столба жидкости (мм рт.ст; м вод.ст.)
Рассмотрим жидкость, находящуюся в покое относительно неинерциальной системы координат x, y, z . Выделим в этой жидкости элементарный параллелепипед с ребрами dx,dy,dz , параллельными соответствующим осям координат. Объем параллелепипеда
dV dxdydz , масса dmdV dxdydz .
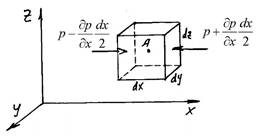 Отбросим жидкость,
окружающую параллелепипед, и заменим действие отброшенной жидкости силами. Это
будут сжимающие поверхностные силы давления.
Отбросим жидкость,
окружающую параллелепипед, и заменим действие отброшенной жидкости силами. Это
будут сжимающие поверхностные силы давления.
Кроме них на жидкость действуют массовые силы, проекции плотности распределения которых на оси координат X,Y,Z .
Массовая сила в направлении оси x составит X dm Xdxdydz
Пусть давление в центре выделенного объема равно p . Давление непрерывная функ-
ция координат, градиент давления в направлении оси x составит ![]() (ограничимся
первой
(ограничимся
первой
производной). Тогда давление на левой грани p ![]() , давление на правой грани
, давление на правой грани
p dx
p ![]() . Составим уравнение равновесия жидкости, заключенной в параллелепипед
. Составим уравнение равновесия жидкости, заключенной в параллелепипед
x 2
(сумма сил равна 0). В проекции на ось x получим
p dx p dx 0
X dxdydzp ![]() dydzp
dydzp ![]() dydz
dydz
x 2 x 2
Раскроем скобки и разделим на массу dmdxdydz . Тогда, с учетом проекций на другие
|
оси, имеем: |
|
|
1 p X
x 1 p Y
y 1 p Z
z
|
(*) Дифференциальные уравнения равновесия жидкости Эйлера.
|
Умножим дифференциальные уравнения равновесия жидкости Эйлера на dx, dy, dz соответственно и сложим (по размерности имеем: Х – сила, действующая на единичную массу, dx– путь, результат умножения – работа)
![]() XdxYdyZdz
xdx
XdxYdyZdz
xdx![]() ydy
ydy ![]() z dz0
z dz0
Давление p зависит от координат, т.е. p f (x, y, z) .
p p p
![]() Полный
дифференциал давления (из математики): dp dx dy dz.
Полный
дифференциал давления (из математики): dp dx dy dz.
x y z
Имеем: dp(XdxYdyZdz) – уравнение равновесия жидкости Эйлера в объединенном виде.
Воспользуемся полученным уравнением для частного случая, когда из массовых сил на жидкость действует только сила тяжести. На элементарную массу dm действует сила веса G dm g в направлении, противоположном оси z. Потенциал массовых сил (отношение сил к массе) в проекциях на оси координат: X 0, Y 0, Z g .
Подставляем в объединенное уравнение Эйлера dp gdz или dz ![]() dp 0
dp 0
g
После интегрирования получаем основное уравнение гидростатики. Для всех точек покоящейся жидкости сумма геометрического и пьезометрического напоров есть величина p
постоянная z
![]()
const
Hг – гидростатический
напор.
const
Hг – гидростатический
напор.
g
На поверхности Земли действует атмосферное давление. Все тела находятся под действием давления столба воздуха. На поверхность жидкости в открытом сосуде всегда действует атмосферное давление, в закрытом сосуде давление может быть, как больше атмосферного (избыточное давление) так и меньше атмосферного (вакуумметрическое давление).
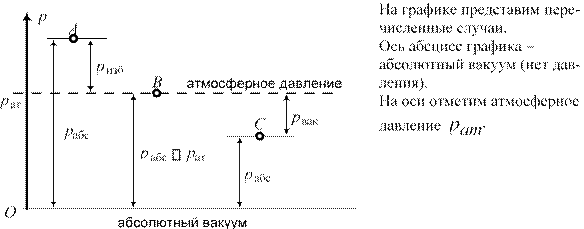
Точка А – абсолютное давление выше атмосферного, избыточное характеризует превышение абсолютного давления над атмосферным, иногда называется манометрическим.
Точка В – абсолютное давление равно атмосферному. Избыточное равно нулю.
Точка С – абсолютное давление меньше атмосферного (вакуум). Вакуумметрическое давление характеризует на сколько абсолютное давление меньше атмосферного. (избыточное давление отсутствует, формально оно отрицательно).
Определения.
Давление абсолютное – характеризует интенсивность напряженного состояния жидкости, отсчитывается от абсолютного нуля давления. (редко : фактическое, реальное).
Давление атмосферное – давление воздуха на поверхности Земли. Принимается равным 1 кг/см2 – техническая атмосфера (98,0665 кПа, 735,559 мм рт. ст.). Редко используется физическая атмосфера = 760 мм рт.ст.
Давление избыточное (манометрическое) – превышение над атмосферным.
pизб p pат .
Давление вакуумметрическое (вакуум) – недостаток до атмосферного. pвак pат p.
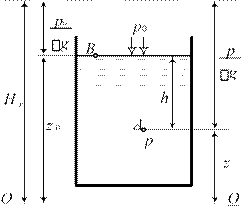 С С На рисунке
изображен сосуд с жидкостью в состоянии покоя.
С С На рисунке
изображен сосуд с жидкостью в состоянии покоя.
Давление на свободной поверхности p0 равно атмосферному давлению. p0 pат .
Точка А выбрана на глубине h , а точка В на свободной поверхности. Положение точек от плоскости сравнения z и z0. Давление в точке А равно p , а в точке В равно давлению на свободной поверхности p0.
![]() Запишем основное
уравнение гидростатики для выбранных точек p p0 или
Запишем основное
уравнение гидростатики для выбранных точек p p0 или
z z0
g g
p p0 g(z0 z).
Заметим, что z0 z h – глубина погружения точки А.
Окончательно формула для определения гидростатического давления в точке p p0 gh.
здесь p0– абсолютное или избыточное давление на поверхности жидкости;
p – соответственно абсолютное или избыточное давление в точке на глубине h жид-
кости плотности в поле силы тяжести. Слагаемое gh называют весовым давлением, т.к. это вес столба жидкости единичной площади высотой h плотностью . Повторим:
если p0 взять абсолютное, то и p (результат) будет абсолютное. Если избыточное, то и результат избыточное. Так если в частном случае на поверхности жидкости давление равно атмосферному, то это значит, что избыточное давление на поверхности равно нулю. Тогда избыточное давление в точке на глубине p gh.
В сосудах находится жидкость, для определенности вода, в состоянии покоя.
Рассмотрим три случая: давление на поверхности равно, больше и меньше атмосферного.
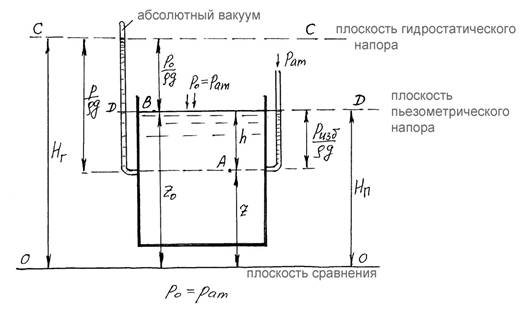
Сосуд с жидкостью под атмосферным давлением
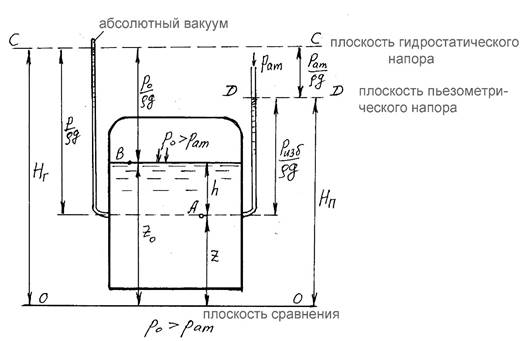
Сосуд с жидкостью под давлением больше атмосферного
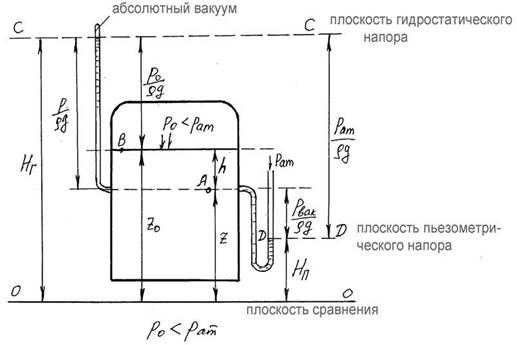
Сосуд с жидкостью под давлением меньше атмосферного
В первом случае сосуд открыт, во втором и третьем случаях сосуды закрыты.
Точка А везде выбрана на некоторой глубине h от поверхности воды, точка В на свободной поверхности. Положение точек А и В относительно плоскости сравнения 0-0 z и z0 . На высоте точки А установлены водяные манометры – запаянные трубки из которых удален воздух (на рисунках слева). Вода в них поднимается на высоту, определяемую абсоp
лютным
давлением ![]() .
Эта высота плюс высота положения точки А составляют гидростаg
.
Эта высота плюс высота положения точки А составляют гидростаg
![]() тический напор Hг , который постоянен для
всех точек покоящейся жидкости (основное p p0 Hг . Геометрическое место
полученных выуравнение гидростатики) z z0
тический напор Hг , который постоянен для
всех точек покоящейся жидкости (основное p p0 Hг . Геометрическое место
полученных выуравнение гидростатики) z z0
g g
сот есть плоскость гидростатического напора С-С.
На высоте точки А установлены также пьезометры – трубки с открытым верхним концом, так что на жидкости в них действует атмосферное давление (на рисунках справа). Вода
в них поднимается на высоту pизб относительно точки А (если давление в точке А меньше ρg
pвак
атмосферного, то уровень воды будет ниже на величину ). Эта высота называется ρg
пьезометрической высотой. Вместе с высотой положения она составляет пьезометрический напор. Геометрическое место полученных высот есть плоскость пьезометрического напора D-D, которая всегда расположена ниже плоскости гидростатического напора на высоту pат . ρg
Основное уравнение гидростатики может быть записано для абсолютного и для избыточного давлений. В обоих случаях геометрическая высота точек, отсчитанная от плоскости сравнения, называется «геометрический напор».
Рассматриваем абсолютные давления. Тогда второе слагаемое – высота, определяемая абсолютным давлением, условно назовем «абсолютный напор». Оба слагаемые дают гидростатический напор.
Рассматриваем избыточные давления. Тогда второе слагаемое – «пьезометрическая высота». В случае вакуума это «вакуумметрическая высота». Вместе с геометрическим напором образуют «пьезометрический напор».
Определения
Плоскость сравнения – горизонтальная плоскость для сравнения высот положения точек жидкости. Положение выбирается исходя из удобства измерений. Обязательное требование – горизонтальность.
Геометрический напор – высота точки от плоскости сравнения.
Пьезометрический напор – высота подъема воды в пьезометре. Определяется избыточным давлением.
Геометрический смысл основного уравнения гидростатики:
для любой точки покоящейся жидкости :
• сумма геометрического напора и напора, соответствующего абсолютному давлению в этой точке, есть величина постоянная, равная гидростатическому напору;
• сумма геометрического напора и пьезометрической высоты есть величина постоянная, равная пьезометрическому напору.
Основное
уравнение гидростатики z ![]() const.
Слагаемые уравнения отнесены g
const.
Слагаемые уравнения отнесены g
к весу единицы объема жидкости, т.е. поделены на g . Поэтому их называют «удельными», т.е. отнесенными к единице (в данном случае к единице веса).
Чтобы перейти к величинам,
отнесенным к элементарной частице жидкости, достаточно умножить на ее вес dm g : p dmg z
dmg ![]()
const
const
g
Первое слагаемое есть сила веса частицы умноженная на высоту ее положения, т. е.
работа, необходимая для поднятия частицы на указанную высоту. Это потенциальная энергия положения.
Второе слагаемое после очевидных сокращений dV p есть работа, необходимая для
«создания» частицы, т.е. высвобождения занимаемого ею объема dV при сопротивлении силы, обусловленной давлением жидкости. Второе слагаемое – «потенциальная энергия давления».
(Подробно поясним это важное замечание: пусть объем частицы изменился от нуля до dV . Для этого граница частицы площадью dydz должна пройти против сил давления, равных произведению давления на ее площадь pdydz путь dx; совершенная работа есть произведение силы на путь pdydzdx pdV . Эту работу иногда называют «работа вытеснения»)
Сумма двух слагаемых есть полная потенциальная энергия частицы.
Переходя вновь к удельным величинам имеем:
Удельная потенциальная энергия положения и удельная потенциальная энергия давления составляют полную удельную потенциальную энергию, называемую гидростатический напор.
1.1.6. Закон Паскаля[2] Сначала приведем полную формулировку закона.
Внешнее давление, производимое на пограничную поверхность жидкости, находящейся в равновесии в замкнутом сосуде, передается во внутрь жидкости одинаково всем ее частицам.
Другая формулировка (более общая)
Изменение давления в любой точке покоящейся жидкости передается в остальные ее точки без изменений.
Применим основное уравнение гидростатики к двум точкам покоящейся жидкости z1 p1 z2 p2 . Изменим давление в первой точке на p1, не нарушая равнове-
g g
сия жидкости. Тогда во второй точке давление должно измениться на некоторое значение p2. Из основного уравнения гидростатики следует, что
z1 p1 p1 z2 p2 p2 или p1 p2, ч. т .д.
g g
Уравнение равновесия жидкости Эйлера в объединенном виде dp (Xdx Ydy Zdz)
Равенство имеет смысл лишь в том случае, если правая его часть также есть полный дифференциал какой-то функции. Обозначим эту функцию через U U(x, y,z). Тогда
U U U
![]() полный дифференциал ее будет dU dx dy dz.
полный дифференциал ее будет dU dx dy dz.
x y z
Примем dp dU .
U U u
Тогда имеем X ![]() , Y
, Y
![]() , Z
, Z ![]() .
.
x dy z
Функцию U U(x, y,z) называют потенциальной функцией, а силы, для которых эта функция существует, – силами, имеющими потенциал.
Отсюда вывод: Жидкость может находится в равновесии только под действием массовых сил, имеющих потенциал, так как только такие силы удовлетворяют уравнениям равновесия Эйлера.
Поверхностью равного давления называют такую выделенную в жидкости поверхность, гидростатическое давление во всех точках которой одно и то же. Очевидно, что для такой поверхности dp 0 и p const. Учитывая dp dU получим dU 0 и U const. Поверхности равного давления и равного потенциала совпадают.
Для жидкости, находящейся в покое под действием силы тяжести уравнение поверхностей равного давления z С (или h C ).
1.1.7. Относительное равновесие
При равновесии в движущемся сосуде жидкость движется вместе с сосудом как единое целое, т.е. находится в состоянии относительного покоя.
Рассмотрим равновесие жидкости, находящейся в сосуде, перемещающемся горизонтально с постоянным положительным ускорением a .
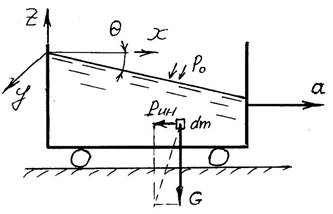
В том случае из массовых сил действуют сила тяжести G dmg и сила инерции Pин dma , направление которой противоположно направлению ускорения.
Проекция плотности распределения силы тяжести Z g , а силы инерции X a
.
Применим уравнение равновесия жидкости Эйлера в объединенном виде dp (Xdx Ydy Zdz) dp adx g dz
После интегрирования p a x g z C
При x y z 0 имеем C p0, окончательно p p0 ax gz.
Уравнение поверхностей равного давления из условия ax gz C получим a a
z
![]() x C. Для свободной
поверхности z
x C. Для свободной
поверхности z
![]() x . Тангенс угла наклона
поверхностей g g
x . Тангенс угла наклона
поверхностей g g
a
равного
давления tg
![]() (не зависит от ).
g
(не зависит от ).
g
Как распределено давление по глубине ? Обозначим h – глубину точки, отсчитанную a
по вертикали от свободной поверхности. Тогда z
![]() x h . Подставим в выражение
для
x h . Подставим в выражение
для
g
давления p p0 ax gz
p0 ax ![]() gag x gh
p0
gh . Распределение
gag x gh
p0
gh . Распределение
давления по глубине подчиняется гидростатическому закону.
В этом случае положительные значения ускорения a соответствуют ускорению, направленному вверх (по оси z), а отрицательные –когда ускорение направлено вниз.
Уравнение поверхностей равного давления z C.
Давление p p0 (g a)h .
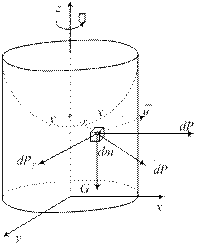 Рассмотрим
цилиндрический сосуд, заполненный до некоторого уровня жидкостью плотностью
и приведенный во вращение с постоянной угловой скоростью
относительно вертикальной оси. Через некоторое время после начала вращения
сосуда жидкость под действием сил трения будет вращаться с той же скоростью,
что и сосуд.
Рассмотрим
цилиндрический сосуд, заполненный до некоторого уровня жидкостью плотностью
и приведенный во вращение с постоянной угловой скоростью
относительно вертикальной оси. Через некоторое время после начала вращения
сосуда жидкость под действием сил трения будет вращаться с той же скоростью,
что и сосуд.
x На элементарную массу dm, расположенную от оси на расстоянии r , действуют силы веса
G dmg и центробежная сила инерции, направ-
2 . ленная вдоль радиуса и равная dPцб dm r Ее проекции на оси координат (из подобия треугольников)
x 2
dPцбx
dPцб ![]() dm
x ,
dm
x ,
r
y 2
dPцбy
dPцб ![]() dm
y
dm
y
r
Проекции вектора плотности распределения массовых сил при этом:
• от силы тяжести X 0, Y 0, Z g
• от центробежной силы инерции X 2x , Y 2y , Z 0.
Применим уравнение равновесия жидкости Эйлера в объединенном виде dp (Xdx Ydy Zdz) dp (2xdx 2ydy g dz)
Для нахождения формы поверхностей равного давления произведем интегрирование при условии dp 0.
2 ![]() (x2 y2) gz C или, поскольку x2 y2 r2, 2
(x2 y2) gz C или, поскольку x2 y2 r2, 2
2 2 2
![]() r
gz
C ,
окончательно z
r
gz
C ,
окончательно z ![]() r2 C1
r2 C1
2 2g
Из полученной формулы ясно, что поверхности равного давления представляют собой семейство конгруэнтных параболоидов вращения с вертикальной осью. Свободная поверхность – частный случай поверхности равного давления, во всех точках которой давление равно внешнему давлению p0. Координаты вершины параболоида x 0, y 0, r 0,
z z0. С1 z0.
2
2
Уравнение свободной поверхности zсв
z0 ![]() r
r
Закон распределения давлений. Используем ранее полученное дифференциальное
2 2
уравнение равновесия жидкости dp ( xdx ydy g dz) . После интегрирования имеем:
p
![]() 22r2 gzC2. Из условий на вершине
параболоида r
0, z z0 ,
22r2 gzC2. Из условий на вершине
параболоида r
0, z z0 ,
p p0 найдем C2 p0 gz0, после подстановки
2 2
r
p p0 ![]() gz0 z
gz0 z
2
Установим, как распределяется давление по вертикали. Для этого подставим в полу-
2 2 r
ченное уравнение выражение из уравнения свободной
поверхности ![]()
zсв
z0. 2g
zсв
z0. 2g
p p0 g(zсв z0) g(z0 z) p0 g(zсв z) p0 gh, где h z св z – глубина погружения точки под свободной поверхностью.
Таким образом, в жидкости, покоящейся в равномерно вращающемся сосуде, давление по вертикали распределяется по гидростатическому закону.
Гидростатическое давление – модуль сжимающего напряжения, возникающего в покоящейся жидкости.
Свойства:
1) направлено всегда по внутренней нормали к площадке, на которую оно действует; 2) в любой точке жидкости по всем направлениям одинаково.
Приборы для измерения давления
Классификация:
По характеру измеряемой величины:
• Барометры – для измерения атмосферного давления pат .
• Манометры – для измерения избыточного давления
• (разницы между абсолютным и атмосферным давлением, т.е. pизб p pат ).
• Вакуумметры – для измерения вакуумметрического давления (разницы между атмосферным давлением и абсолютным, т.е. pвак pат p).
• Дифференциальные манометры – для измерения разности давлений. Микроманометры – для измерения малых давлений и малых перепадов давления.
По принципу действия различают приборы жидкостные, пружинные, поршневые, электрические, комбинированные и др.
По классу точности образцовые, контрольные и рабочие.
Класс точности численно равен
отношению допустимой абсолютной ошибки измерения прибора
к верхнему пределу измерения pмакс в процентах K
![]() pмакс 100 .
pмакс 100 .
К = 0.25 ; 0.4 ; 0.6 – образцовые и контрольные; К = 1.0 ; 1.5 ; 2.4 ; 4.0 – рабочие.
К жидкостным приборам для измерения давления относятся пьезометры, манометры, вакуумметры, дифференциальные манометры.
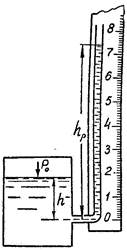 Пьезометры применяются
для измерения избыточного и вакуумметрического давления.
Пьезометры применяются
для измерения избыточного и вакуумметрического давления.
Верхний конец пьезометра (стеклянной трубки) сообщается с атмосферой. Избыточное давление определяется по формуле pизб ghр , где hр - высота поднятия жидкости над изме-
ряемой точкой.
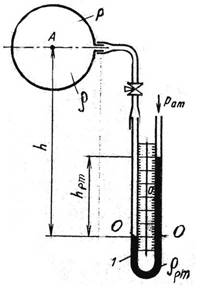 U – образный
манометр представляет собой U – образную стеклянную трубку, заполненную
рабочей жидкостью. Обычно в качестве рабочих жидкостей используют воду, спирт,
ртуть, тетрабромэтан, бромистый этилен, бромистый этил. (глицерин, ЛР№4)
U – образный
манометр представляет собой U – образную стеклянную трубку, заполненную
рабочей жидкостью. Обычно в качестве рабочих жидкостей используют воду, спирт,
ртуть, тетрабромэтан, бромистый этилен, бромистый этил. (глицерин, ЛР№4)
Давление на плоскости 0-0, называемой плоскостью сравнения, обозначим p* слева: p* pАабс gh справа: p* pат ртghрт
Избыточное давление в сосуде
pАизб pAабс pат ртghрт gh.
Здесь – плотность жидкости в сосуде, заполняющей
левое колено диффманометра. Если это воздух, плот-
ность которого в 800 раз меньше плотности воды, то ею можно пренебречь. Тогда pAизб ртghрт.
Замечание. Использование ртути запрещено не только в учебных учреждениях, но и на производстве.
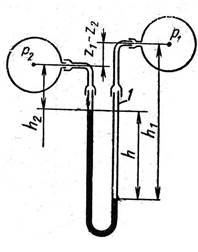 Дифференциальные
манометры применяются для измерения разности давлений в двух точках
покоящейся и движущейся жидкости.
Дифференциальные
манометры применяются для измерения разности давлений в двух точках
покоящейся и движущейся жидкости.
слева p* p2 gh2 ртghрт справа p* p1g(hрт h2 z1 z2)
p1 p2 ghртрт gz1 z2.
Разность одинакова для абсолютных и избыточных давлений.
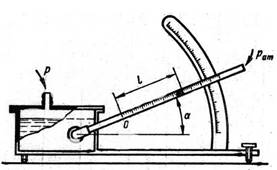 Микроманометры
с наклонной трубкой и наклонной шкалой позволяют измерять с большей точностью
малые давления газов. Избыточное давление на поверхности жидкости в чашке равно
Микроманометры
с наклонной трубкой и наклонной шкалой позволяют измерять с большей точностью
малые давления газов. Избыточное давление на поверхности жидкости в чашке равно
pизб жglsin,
где ж - плотность жидкости;
- угол наклона трубки к горизонту.
Основными преимуществами жидкостные приборов является простота устройства и высокая точность измерений.
Принцип действия пружинных приборов основан на упругой деформации упругого элемента (трубчатой пружины, мембраны или сильфона) под действием давления. Деформация элемента пропорциональна величине измеряемого давления.
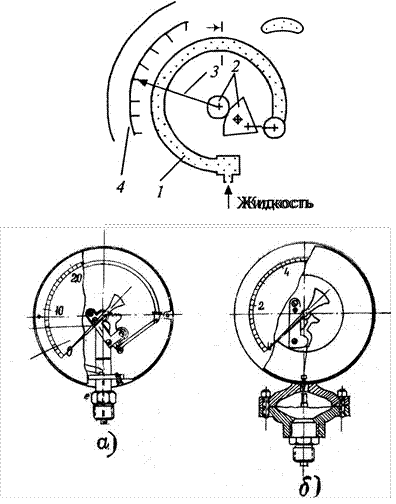
Пружинный манометр:
а – с трубчатой пружиной; б – с мембраной
Из металлических приборов наиболее распространенным на практике является пружинный манометр (см. рис.), принцип действия которого следующий.
Под действием давления жидкости полая пружина 1 частично распрямляется и посредством зубчатого механизма 2 приводит в движение стрелку 3, перемещающуюся относительно шкалы 4. Принцип действия пружинного манометра основан на уравновешивании силы давления жидкости упругой силой пружины. Пружинный манометр показывает избыточное давление.
Основной деталью прибора является согнутая по дуге окружности полая трубка, имеющая в сечении овальную форму (трубка Бурдона). Один из концов трубки запаян. Под действием давления свободный конец трубки поворачивается на некоторый угол, пропорциональный измеряемому давлению. При этом с помощью поводка поворачивается зубчатый сектор, который поворачивает шестеренку, с осью которой жестко связана стрелка.
Недопустимо подавать на манометры с упругим элементом давление больше максимально допустимого по паспорту прибора (и меньше – вакуум). Остаточная деформация упругого элемента неустранима, прибор испорчен.
В грузопоршневых приборах величина давления определяется по весу грузов, помещаемых на рабочей площадке поршня, под которым создано измеряемое давление.
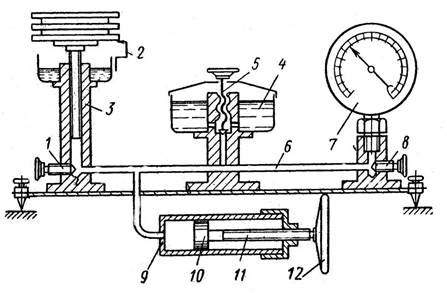
Грузопоршневой манометр
Установка для поверки пружинных манометров по образцовому пружинному манометру вместо цилиндра 3 содержит устройство для присоединения образцового прибора. При поверке любого прибора сравнивают показания поверяемого прибора с показаниями образцового.
Приемным элементом электрических приборов, преобразующим величину деформации упругого элемента, пропорциональную давлению, в тот или иной электрический сигнал, является датчик давления.
Используются датчики:
• индуктивные (дифференциальный трансформатор с подвижн. сердечником),
• емкостные,
• пьезоэлектрические, полупроводниковые
• датчики сопротивления.
Важно для использования в системах управления и защиты – выходной сигнал электрический.
Точность механических и электрических манометров достигает 0,1 % максимального значения шкалы.
Эпюра гидростатического давления – графическое изображение закона распределения нормального гидростатического напряжения по поверхности. Давление можно рассматривать абсолютное, избыточное и весовое (только за счет жидкости). Если давление на поверхности жидкости совпадает с атмосферным давлением, то избыточное и весовое давления совпадают. Эпюры могут быть построены для всех перечисленных давлений, однако на практике строят обычно эпюры избыточного давления, принимая во внимание, что с другой стороны стенки также действует атмосферное давление.
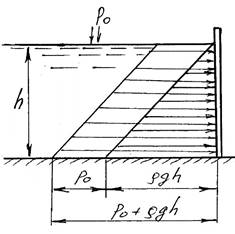 Эпюру всегда следует
строить со стороны жидкости, помня о направлении действия нормальных напряжений
в покоящейся жидкости (по внутренней нормали).
Эпюру всегда следует
строить со стороны жидкости, помня о направлении действия нормальных напряжений
в покоящейся жидкости (по внутренней нормали).
На свободной поверхности имеем pабс p0, pизб 0 . На глубине h
pабс p0 gh, pизб gh
1. Поверхность горизонтальна
Все точки горизонтальной площадки находятся на одинаковой глубине и испытывают одинаковое давление со стороны покоящейся жидкости. Если свободная поверхность жидкости открыта в атмосферу ( p0 pат), то сила избыточного давления на площадку площади F определяется по формуле Pизб ghF , т.е. численно равна весу жидкости, заключенной в вертикальной призме с основанием F и высотой h .
Сила Pизб направлена со стороны жидкости перпендикулярно стенке. Линия действия силы пересекает площадку F в центре тяжести, так как давление распределено по площадке равномерно. При равенстве p0, плотностей , площадей оснований F и глубин h независимо от формы сосуда сила давления на горизонтальное дно будет одной и той же. Так в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, в цилиндрических – они одинаковы, а в сужающихся кверху – сила давления больше веса заключенной в сосуд жидкости. Это явление, парадоксальное с точки зрения житейских представлений, носит название «гидростатический парадокс». (Б. Паскаль).
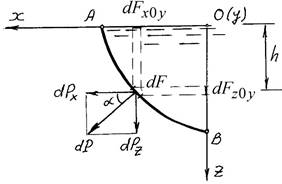
2. Поверхность наклонна
 Рассмотрим плоскую
фигуру площадью F (часть
наклонной стенки). На рисунке эта фигура условно развернута. Выделим
элементарную площадку dF ,расположенную
на глубине h , на
которую действует элементарная сила dP pdF
p0 ghdF со стороны жидкости по
нормали к площадке. Сила, действующая на всю площадь F , направлена также по
Рассмотрим плоскую
фигуру площадью F (часть
наклонной стенки). На рисунке эта фигура условно развернута. Выделим
элементарную площадку dF ,расположенную
на глубине h , на
которую действует элементарная сила dP pdF
p0 ghdF со стороны жидкости по
нормали к площадке. Сила, действующая на всю площадь F , направлена также по
нормали.
F F
Очевидно h ysin, причем sinвеличина постоянная, выносится за знак интеграла.
Известно, что интеграл ydF S0x ycF есть статический момент плоской фиF
гуры относительно оси 0x и равен произведению координаты центра тяжести плоской фигуры на ее площадь.
P p0dF ghdF p0 dF gsinydF p0F gsinycF
F F F F
Воспользуемся соотношениями yc sin hc и pc p0 ghc :
P p0 ghc F pcF .
Сила, действующая на плоскую стенку со стороны жидкости, равна произведению давления в центре тяжести на площадь. Центр давления – точка приложения равнодействующей силы давления жидкости на плоскую поверхность (точка d ).
Для нахождения координаты yd воспользуемся теоремой Вариньона[3] рассматривая момент сил относительно оси 0x (на рисунке точка 0).
ydP ydP Отсюда находим yd : F
2
![]() ydP
y(p0 gh)dF p0 ydF gsin
y dF yd
F F F F
ydP
y(p0 gh)dF p0 ydF gsin
y dF yd
F F F F
P P P
Известно, что момент инерции плоской фигуры относительно оси 0x
J0x y dF
2 выразим через момент инерции плоской фигуры относительно оси,
F
2 приходящей через центр тяжести (параллельный перенос оси) J0x Jc ycF . Окончательно:
2
![]() yd
p0ycF gsin(Jc
yc F) .
yd
p0ycF gsin(Jc
yc F) .
(p0 ghc)F
Если стенка вертикальная, то формула упрощается, т.к. yс hc, sin1:
2
p
![]() hd 0hcF g(Jc hc F) .
hd 0hcF g(Jc hc F) .
(p0ghc)F
Если на поверхности жидкости избыточное давление равно нулю ( p0 0 ), то формула упрощается
2
![]() yd gsinJc gsin yc F Jc yc
yd gsinJc gsin yc F Jc yc
gsin ycF ycF
![]() Jc
Jc
Окончательно координата центра давления yd yc
ycF
![]() Величину Jc
0 называют
эксцентриситетом. Напомним: Jc – момент инерции ycF
Величину Jc
0 называют
эксцентриситетом. Напомним: Jc – момент инерции ycF
плоской фигуры относительно горизонтальной оси, проходящей через центр тяжести.
Моменты инерции плоских фигур относительно горизонтальной оси, проходящей через центр тяжести (для справки)
|
|
Круг |
|
d – диаметр |
4 d Jc |
|
ник |
Прямоуголь- |
|
h – высота b– ширина |
3 bh Jc |
|
|
Квадрат |
|
a – сторона |
4 a Jc |
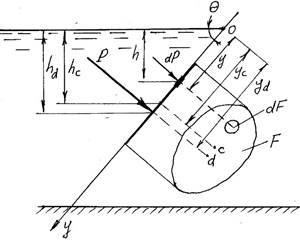
Рассмотрим некоторую ограниченную часть твердой цилиндрической поверхности AB, которую назовем цилиндрической стенкой. Образующая стенки параллельна оси 0y
.
 Пусть рассматриваемая
стенка находится под односторонним воздействием покоящейся жидкости.
Пусть рассматриваемая
стенка находится под односторонним воздействием покоящейся жидкости.
Выделим элементарную площадку dF , ее проекции на координатные плоскости dFx0y и dFz0y .
Нормально к площадке со стороны жидкости действует сила dP, ее проекции на оси dPx и dPz .
Элементарная сила равна произведению давления на площадь dP pdF p0 ghdF
Проекция элементарной силы на ось x , учитывая, что dFz0y dFcos dPx dPcos p0 ghdFcos p0 ghdFz0y
Проекция элементарной силы на ось z, учитывая, что dFx0y dFsin dPz dPsin p0 ghdFsin p0 ghdFx0y Интегрированием найдем проекции силы, действующей на всю площадь стенки F .
На ось x :
Px dPx p0 ghdFz0y p0 dFz0y g hdFz0y
F Fz0y Fz0y Fz0y
Учтем выражение для статического момента плоской фигуры Fz0y относительно оси
0y
S0y hdFz0y hcFz0y,
Fz0y где hc – глубина погружения центра тяжести проекции Fz0y .
Px p0Fz0y ghcFz0y (p0 ghc)Fz0y
На ось z:
Pz dPz p0 ghdFx0y p0 dFx0y g hdFx0y
F Fx0y Fx0y Fx0y
Заметим, что hdFx0y dVтд – объем призмы высотой h , опирающейся на площадку dF и ограниченной сверху свободной поверхностью жидкости.
hdFx0y Vтд – объем «тела давления».
Fx0y
Определение. Тело давления – призма, ограниченная снизу криволинейной поверхностью, с боков вертикальными плоскостями, проходящими через крайние образующие поверхности, сверху поверхностью жидкости (или ее продолжением).
Pz p0Fx0y gVтд p0Fx0y Gтд .
Здесь Gтд – вес жидкости в объеме тела давления.
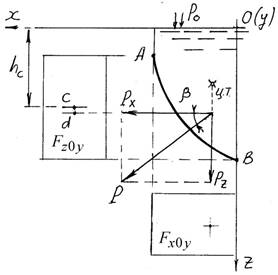 Окончательно:
Окончательно:
Px (p0 ghc)Fz0y Pz p0Fx0y Gтд
2 2
![]() Р Px
Pz
Р Px
Pz
Pz
tg
Px
Если давление на свободной поверхности равно атмосферному, то избыточное давление p0 0 и формулы упрощаются: Px ghcFz0y и Pz Gтд
Линия действия Px проходит через центр давления (точка d ) площади проекции Fz0y , а линия действия силы Pz проходит через центр тяжести тела давления.
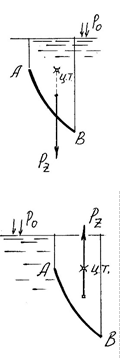 Если тело давления и
жидкость находятся с одной стороны поверхности (жидкость заполняет тело
давления), то сила Pz направлена вниз.
Если тело давления и
жидкость находятся с одной стороны поверхности (жидкость заполняет тело
давления), то сила Pz направлена вниз.
Если тело давления и жидкость находятся с разных сторон поверхности (жидкость не заполняет тело давления), то сила Pz направлена вверх (выталкивающая сила).
Формулировка. Сила давления покоящейся жидкости на тело, погруженное в нее, равна весу вытесненной телом жидкости, направлена вверх и приложена в центре тяжести вытесненного объема.
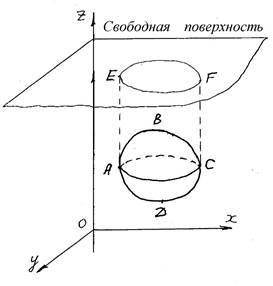 Доказательство
проведем, используя вывод для силы давления на криволинейную стенку.
Доказательство
проведем, используя вывод для силы давления на криволинейную стенку.
Рассмотрим тело, погруженное в жидкость. Условно разделим тело на верхнюю и нижнюю половины сечением AC . Сила давления на верхнюю половину направлена вниз и равна весу жидкости в теле давления ABCFE .
Рв GABCFE
Сила давления жидкости на нижнюю половину направлена вверх и равна весу жидкости в теле давления ADCFE .
Рн GADCFE
PA Pн Pв GABCD
Сила Архимеда направлена вверх и равна весу жидкости в объеме ABCD , ч.т.д.
В заключение раздела гидростатики рассмотрим напряжения, возникающие в стенке круглого трубопровода, находящегося под давлением жидкости.
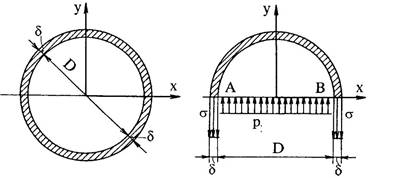
Рассмотрим отрезок трубы длиной b. Сила давления жидкости на стенку трубопровода есть произведение давления p на площадь действия bd : Pж pbd .
Эта сила уравновешивается нормальными растягивающими напряжениями в стенке трубопровода , действующими на площади 2b : Pст 2b После очевидных преобразований получаем: pd
![]()
Эта формула, связывающая нормальные напряжения в стенках трубопровода с давлением внутри него, называется «котельной формулой». Из нее, зная допустимое напряжение на разрыв материала стенки [р], можно найти минимальную толщину стенки
pD
мин ![]() . При проектировании нужно учесть еще коэффициент запаса. 2[p]
. При проектировании нужно учесть еще коэффициент запаса. 2[p]
Выше рассматривались напряжения в стенках, направленные перпендикулярно оси трубопровода. Рассмотрим напряжения, направленные параллельно оси трубопровода.
2
d
Давление вдоль оси действует на
площадь ![]() ,
а напряжение в стенке распределено
,
а напряжение в стенке распределено
4
по площади d.
Приравняв, получим l ![]() . Значение напряжения в стенке, направ-
. Значение напряжения в стенке, направ-
ленное вдоль оси в 2 раза меньше, чем напряжение, направленное поперек оси. Именно поэтому сосиски при варке рвутся вдоль, а не поперек.
Тема 1.2. Основы гидродинамики
Кинематика жидкости – раздел гидромеханики, в котором изучают виды и характеристики движения жидкости, но не рассматривают силы, под действием которых это движение происходит.
Модель жидкости – совокупность жидких частиц, заполняющих объем без пустот и разрывов.
Жидкая частица – часть жидкости, малая по сравнению с объемом жидкости, но достаточно большая, чтобы пренебречь молекулярной структурой.
Полюс жидкой частицы – центр тяжести. Движение рассматривается отдельно как движение полюса, вращение вокруг полюса и деформация частицы.
Методы описания движения жидкости
1. Метод Лагранжа[4] – рассматривается движение каждой частицы жидкости.
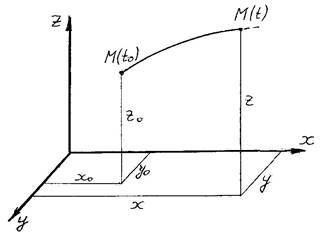 В начальный момент времени каждая частица имеет координаты
x0, y0, z0.
В начальный момент времени каждая частица имеет координаты
x0, y0, z0.
При движении частицы ее координаты зависят от времени: x x(x0, y0,z0,t)
Здесь x0, y0, z0,t – параметры Лагранжа.
x y z
Проекции скорости частицы u на оси ux ![]() ;
uy
;
uy ![]() ;
uz
;
uz ![]() .
.
t t t
![]()
![]() ax ux
t22x ; ay uty
2t2y ;
ax ux
t22x ; ay uty
2t2y ;
Проекции ускорения на оси
2
![]() uz
z
uz
z
az t t2 .
Метод Лагранжа используется редко, только при решении специальных задач.
2. Метод Эйлера (метод описания движения жидкости)
Метод Эйлера изучает поля векторных или скалярных величин, оставляя в стороне вопрос о движении каждой частицы.
Движение жидкости описывается функциями, выражающими изменения скоростей в точках некоторой неподвижной области, выбранной в пределах потока. В данный момент времени в каждой точке этой области, определяемой координатами x, y,z находится частица жидкости, имеющая скорость u . Эту скорость называют мгновенной местной скоростью. Совокупность мгновенных местных скоростей представляет векторное поле, называемое полем скоростей.
Скалярное поле – область пространства, каждой точке которой поставлено в соответствие значение некоторой скалярной величины. Векторное поле – область пространства, каждой точке которой поставлено в соответствие значение некоторой векторной величины. В общем случае оно может изменяться по времени и по координатам:
![]()
u uxi uy j uzk ;
ux ux(x, y,z,t)
uy uy(x, y,z,t)
uz uz(x, y,z,t)
Переменные x, y,z,t называют переменными Эйлера.
![]() Ускорение жидкой частицы в
проекциях на оси координат dux
, duy , duz .
Ускорение жидкой частицы в
проекциях на оси координат dux
, duy , duz .
dt dt dt
![]() Из математики полный
дифференциал функции нескольких переменных dux ux dt
ux dx
ux dy
ux dz.
Из математики полный
дифференциал функции нескольких переменных dux ux dt
ux dx
ux dy
ux dz.
t x y z
Замечание. В общем случае dx,dy,dz произвольны, однако будем полагать, что это проекции элементарного перемещения ds жидкой частицы на оси координат, тогда dx dy dz
![]() ux,
ux, ![]()
uy,
uy, ![]()
uz . dt dt dt
uz . dt dt dt
Полная производная скорости по времени (полное ускорение) в проекции на ось x и аналогично на другие оси:
![]()
![]()
![]() dux ux
uxx
ux
uyx
uy
uzx
uz
dt t
dux ux
uxx
ux
uyx
uy
uzx
uz
dt t
duy uy uy uy uy
![]()
ux
ux
![]() uy
uy
![]() uz
dt t x y z
uz
dt t x y z
![]()
![]()
![]() duz uz
uz ux
uz uy
uz uz
dt t x y z
duz uz
uz ux
uz uy
uz uz
dt t x y z
Здесь в каждой строке:
•
![]() первое
слагаемое ux – локальная
производная (локальное ускорение) t
первое
слагаемое ux – локальная
производная (локальное ускорение) t
u
• ![]()
![]()
![]() трехчленная сумма x ux
ux uy
ux uz – конвективная
производная (конвек-
трехчленная сумма x ux
ux uy
ux uz – конвективная
производная (конвек-
x y z
тивное ускорение), поскольку оно определяет ускорение частицы при изменении ее положения в поле скоростей (конвекции) .
Полную производную иногда называют субстанциальной ( от слова «субстанция») производной.
Если движение установившееся, т.е. не зависит от времени, то локальные производные равны нулю:
![]() ux
uy
uz
0
ux
uy
uz
0
t t t
Если движение плоское, т.е. скорости на зависят от z и установившееся, то
![]()
![]() dudtx uxx ux uyx uy
dudtx uxx ux uyx uy
![]() dudty uxy ux
dudty uxy ux ![]() uyy uy
uyy uy
Если движение одномерное, то имеем ускорение жидкой частицы (по обозначению u ux ): du u
![]()
u . dt x
u . dt x
Метод Эйлера описывает движение жидкости через поле скоростей и поэтому ускорения жидкой частицы в нем выражаются специальной «субстанциальной» производной, а не как в технической механике.
Линия тока – кривая, в каждой точке которой вектор скорости направлен по касательной к ней.
![]()
Для плоского движения dy
на линии тока ![]()
tg
dx
tg
dx
из соотношения проекций ско-
uy
рости
![]()
tg
tg
ux
Уравнение линии тока
dx dy
![]() на плоскости:
на плоскости:
dx dy dz
![]() для трехмерного движения .
для трехмерного движения .
ux(x, y, z,t) uy(x, y, z,t) uz(x, y, z,t)
Через произвольную точку потока может проходить лишь одна линия тока => Линии тока не пересекаются. (исключение – особые точки потока).
Траектория частицы – геометрическое место последовательных положений элементарной жидкой частицы в пространстве.
Траектория частицы это характеристика потока по методу Лагранжа, а линия тока – характеристика потока по методу Эйлера. В установившемся движении совпадают.
Трубка тока – поверхность, образованная системой линий тока, проходящих через точки малого замкнутого контура.
![]()
Пояснение: если в сечении потока провести малый не пересекающий себя контур и через каждую точку его провести линию тока, то полученная поверхность называется трубка тока. Если контур ограничивает бесконечно малую площадку, то получится элементарная трубка тока.
Элементарная струйка – жидкость, заключенная в элементарной трубке тока.
Свойства элементарной струйки 1. При установившемся движении ее форма не меняется.
2. Является непроницаемой для жидкости
3. Скорость в пределах сечения можно считать постоянной
Поток жидкости – совокупность элементарных струек, движущихся через площадь больших (конечных) размеров (с разными скоростями).
Бывают безнапорные, напорные потоки и гидравлические струи.
Характеристики потока
1. Живое сечение потока – сечение, во всех точка которого линии тока, пересекающие его нормальны к нему. Площадь живого сечения потока есть сумма площадей живых сечений составляющих его элементарных струек F dF .
F
2. Смоченный периметр – длина линии, по которой живое сечение потока соприкасается с твердыми поверхностями, ограничивающими поток. Обозначается («хи», греч.)
3. Гидравлический радиус – отношение площади живого сечения потока к смоченному периметру. Обозначается Rг .
Примеры потоков.
Напорный трубопровод круглого поперечного сечения (внутренний радиус трубы r ):
• площадь живого сечения F r2 смоченный периметр 2r
![]() F r2 r d гидравлический радиус Rг
2r
2 (
обратить внимание: Rг
F r2 r d гидравлический радиус Rг
2r
2 (
обратить внимание: Rг
![]() 4 )
4 )
Открытое русло шириной b и глубиной h :
• площадь живого сечения F bh смоченный периметр b 2h
F bh
• ![]() гидравлический радиус Rг
гидравлический радиус Rг
b 2h
• для широкого потока при b h имеем Rг h.
4. Расход жидкости в потоке – объемное количество жидкости, протекающее через живое сечение потока в единицу времени.
Расход через живое сечение элементарной струйки dQ udF .
Пояснение: скорость в пределах живого сечения элементарной струйки можно считать одинаковой u , площадь сечения dF . За время dt сечение струйки переместится на ds udt . Прошедший через сечение объем dV dsdF . Объемный расход dV dsdF ds
![]() dQ
dF
udF dt dt st
dQ
dF
udF dt dt st
Чтобы найти расход по всему потоку интегрируем по площади потока Q udF. F
Единицы измерения объемного расхода Q
м3![]() с
с
3 3
![]() также
используются л
также
используются л![]() с, м3
с, м3![]() ч, см3
ч, см3![]() с . Очевидно 1л 1дм 103
с . Очевидно 1л 1дм 103 ![]() см .
см .
В гидравлике по умолчанию расход всегда объемный.
Если имеется в виду массовый
расход, то это оговаривается особо. Массовый расход обозначается M , измеряется кг![]() с .
с .
Для газов (как сжимаемых жидкостей) используется массовый расход
М Q F .
5. Средняя скорость в потоке – частное от деления расхода на площадь живого сечения потока. Обозначается ( в отличие от местной скорости u ).
Пояснение. Средняя скорость в сечении одинаковую для всех точек сечения воображаемую скорость, при которой через данное живое сечение проходит тот же расход, что и при действительных местных скоростях, разных в различных точках сечения.
1.2.3. Виды движения жидкости
1. Неустановившееся (нестационарное) – параметры меняются во времени. u u(x, y,z,t) p p(x, y,z,t)
При этом линии тока не совпадают с траекториями частиц.
![]() Пример – истечение из
отверстия при переменном напоре.
Пример – истечение из
отверстия при переменном напоре.
1-поток в первый момент времени 2-поток в момент, когда точка частица из точки A1 переместилась в точку A2 . Траектория частицы A1 A2.
По характеру изменения скоростей во времени неустановившиеся движения подразделяются на быстро изменяющиеся и медленно изменяющиеся.
Медленно изменяющиеся часто называют также квазиустановившимися (квазистационарными). («квази» лат.– якобы, почти, как бы).
2. Установившееся (стационарное) – параметры не меняются во времени.
![]()
Локальные производные равны нулю. uu(x, y,z) p p(x, y,z)
Линии тока совпадают с траекториями частиц.
Пример – истечение из отверстия при постоянном напоре.
Установившееся движение по характеру изменения скоростей подразделяется на равномерное и неравномерное.
![]() Равномерное движение
Равномерное движение
Линии тока параллельны и прямолинейны.
Размеры и форма живых сечений и средние скорости потока по его длине не меняются.
F1 F2 1 2
Местные скорости в соответствующих точках живых сечений одинаковы. Ускорения при равномерном движении потока равны нулю.
![]() Неравномерное
движение Линии тока не параллельны. Площади живых сечений и средние скорости
переменны по длине потока. Такое движение бывает ускоренное и замедленное
Неравномерное
движение Линии тока не параллельны. Площади живых сечений и средние скорости
переменны по длине потока. Такое движение бывает ускоренное и замедленное
В зависимости от характера и сочетания ограничивающих поток поверхностей потоки делят на безнапорные, напорные и гидравлические струи.
Безнапорные потоки – ограничены частично твердой, частично свободной поверхностью.
Напорные потоки – ограничены твердой поверхностью, испытывающей давление потока, поток заполняет все сечение.
Гидравлические струи – ограничены только жидкостью или газом.
1.2.4. Уравнение постоянства расхода для потока жидкости и газа
![]() Рассмотрим установившееся движение потока жидкости или
газа, ограниченного твердыми непроницаемыми стенками. Выделим в потоке два
сечения 1-1 и 2-2. Массовый расход через выбранные сечения обозначим М1 и M2 .
Рассмотрим установившееся движение потока жидкости или
газа, ограниченного твердыми непроницаемыми стенками. Выделим в потоке два
сечения 1-1 и 2-2. Массовый расход через выбранные сечения обозначим М1 и M2 .
В установившемся движении M1 M2 idem , т. к. в жидкости не образуется пустот и разрывов и масса не может вытекать через стенки.
Замечание: (idem – неизменный const – постоянный).
Вспомним, что M Q и Q F и получим:
11F1 22 F2 idem Уравнение постоянства расхода для потока сжимае-мой жидкости (газа)
Если жидкость несжимаема, то 1 2 const . В этих условиях:
1F1 2 F2 idem Уравнение постоянства расхода для потока несжима-емой жидкости
Иногда эти уравнения называют уравнениями неразрывности для потока жидкости или газа.
1.2.5. Уравнение неразрывности для несжимаемой жидкости в дифференциальной форме
![]() Выделим в области,
занятой движущейся жидкостью, неподвижный бесконечно малый параллелепипед
(кубик), у которого ребра dx,dy,dz
параллельны соответствующим осям координат.
Выделим в области,
занятой движущейся жидкостью, неподвижный бесконечно малый параллелепипед
(кубик), у которого ребра dx,dy,dz
параллельны соответствующим осям координат.
Выделенный кубик неподвижен в пространстве, а через его грани протекает несжимаемая жидкость. Очевидно, что масса входящей за время dtжидкости равна массе выходящей за то же время жидкости.
Сначала рассмотрим грани перпендикулярные оси x , левую и правую. Их площадь одинакова: dydz .
Скорость втекающей через левую грань жидкости ux можно считать одинаковой по всей грани. Тогда за время dt через левую грань войдет масса dmx _вх uxdydz.
По гипотезе сплошности скорость жидкости ux есть непрерывная дифференцируемая функция своих аргументов. Тогда скорость жидкости на правой грани, которая отстоит
![]() ux dx. от левой на расстояние
dx составит ux
ux dx. от левой на расстояние
dx составит ux
![]() ux dxdydz.
ux dxdydz.
Выходящая за время dtчерез правую грань масса dmx_вых ux
Изменение массы жидкости в объеме параллелепипеда за счет входа и выхода жидкости через левую и правую грани:
dmx dmx_вх dmx_вых dxdydzdt
Аналогичные выражения могут быть получены по двум другим осям, т.е. по двум другим парам граней. Общее изменение массы следует приравнять нулю: dm dmx dmy dmz 0
![]() dxdydzdt
xx
yy uzz 0
dxdydzdt
xx
yy uzz 0
Понятно, что левая часть равна нулю только если выражение в скобках равно нулю.
|
x y z |
Уравнение неразрывности для несжимаемой жидкости в дифференциальной форме. |
![]()
![]() Из математики известно: ux
uy
uz
divu ,
Из математики известно: ux
uy
uz
divu ,
x y z
![]() где
divu –
дивергенция ( расходимость) векторного поля в данной точке.
где
divu –
дивергенция ( расходимость) векторного поля в данной точке.
Определение. Предел отношения потока П поля через некоторую замкнутую поверхность S к объему, ограниченному поверхностью S, когда S стягивается в точку М, называется дивергенцией, или расходимостью, поля в точке М.
![]() divu 0
divu 0
Другая форма записи уравнения неразрывности …
![]() Попытаемся
найти геометрический смысл слагаемых вида ux .
Попытаемся
найти геометрический смысл слагаемых вида ux .
![]() Рассмотрим грань dx (ребро кубика).
Скорость левого ее конца ux
, а скорость правого конца ux ux dx. За время dt ребро не только
переместится в пространстве, но и x
Рассмотрим грань dx (ребро кубика).
Скорость левого ее конца ux
, а скорость правого конца ux ux dx. За время dt ребро не только
переместится в пространстве, но и x
![]() за
счет разности скоростей его концов удлинится (деформируется) на величину ux dxdt x
за
счет разности скоростей его концов удлинится (деформируется) на величину ux dxdt x
![]() . Скорость удлинения ребра
составит ux dx, а относительная
скорость деформации ребра x
. Скорость удлинения ребра
составит ux dx, а относительная
скорость деформации ребра x
![]() можно
найти, если поделить эту скорость на длину грани dx. Получим ux .
можно
найти, если поделить эту скорость на длину грани dx. Получим ux .
x
Уравнение неразрывности для несжимаемой жидкости в дифференциальной форме можно истолковать так: сумма скоростей относительной деформации ребер жидкой частицы равна нулю. Жидкость движется так, что данная масса все время занимает один и тот же объем.
Гидродинамика изучает движение жидкости с учетом сил, вызывающих это движение.
Массовые внешние силы, действующие на жидкость, как правило известны и заданы проекциями плотности распределения равнодействующей на оси координат X,Y,Z . Плотность жидкости полагается постоянной и известной.
Задача гидродинамики – определить кинематические характеристики движения и возникающие напряжения, т.е. найти зависимость величин ux,uy,uz и давления p от координат x, y,z и времени.
1.2.6. Дифференциальные уравнения движения идеальной жидкости Л. Эйлера
Рассмотрим элементарный параллелепипед (кубик) жидкости с ребрами dx,dy,dz , параллельными осям координат. Эта жидкая частица движется относительно неподвижной системы координат. Точка А – полюс (в центре тяжести).
![]() Воспользуемся вторым
законом Ньютона применительно к жидкой частице. Произведение массы частицы на
ускорение ее центра масс равно сумме всех внешних сил, действующих на частицу.
Силы и ускорение будем рассматривать в проекции на оси координат (на ось x рассмот рим, на остальные
аналогично). Масса частицы : dxdydz .
Воспользуемся вторым
законом Ньютона применительно к жидкой частице. Произведение массы частицы на
ускорение ее центра масс равно сумме всех внешних сил, действующих на частицу.
Силы и ускорение будем рассматривать в проекции на оси координат (на ось x рассмот рим, на остальные
аналогично). Масса частицы : dxdydz .
![]() Ускорение в проекции на ось x : dux dt
Ускорение в проекции на ось x : dux dt
Поверхностные силы – это силы нормального давления окружающей частицу жидкости. Они равны произведению давления на площадь грани. Рассмотрим грани, перпендикулярные оси x , их площадь dydz . Пусть в полюсе давление равно p .
Давление на левую грань p ![]() ,
на правую грань p
,
на правую грань p ![]() .
.
p dx p dx
Сила на левую грань p ![]() dydz , на правую грань
p
dydz , на правую грань
p ![]() dydz.
dydz.
x 2 x 2
p
Равнодействующая поверхностных сил в проекции на ось x : dxdydz ![]() .
.
x Массовые силы в проекции на ось x : X dm X dxdydz .
Сумма сил равна произведению массы на ускорение ( в проекции на ось x ):
X dxdydzdxdydz ![]() dxdydz
dxdydz
Разделим на массу dxdydz и аналогично запишем проекции на другие оси
|
1 p du X
x dt 1 p duy Y
y dt 1
Z z dt |
Дифференциальные уравнения движения невязкой жидкости Л. Эйлера (1755 г.) |
![]()
![]() Можно развернуть выражение
для ускорения, учитывая что скорость есть не только функция времени, но и
координат. При описании метода Эйлера на прошлой лекции было получено выражение
(например – в проекции на ось x : dux
ux
ux ux
ux uy
ux uz dt t x y z
Можно развернуть выражение
для ускорения, учитывая что скорость есть не только функция времени, но и
координат. При описании метода Эйлера на прошлой лекции было получено выражение
(например – в проекции на ось x : dux
ux
ux ux
ux uy
ux uz dt t x y z
Дифференциальные уравнения движения невязкой жидкости в развернутом виде запишутся:
X ![]()
![]() 1 px utx
uxx
ux
uyx
uy
uzx
uz
1 px utx
uxx
ux
uyx
uy
uzx
uz
1 p uy uy uy uy
Y ![]() ux uy
ux uy ![]() uz
uz
y t x y z
1 ![]()
![]() p uz
uz ux
uz uy
uz uz
p uz
uz ux
uz uy
uz uz
Z
z t x y z
В задачах динамики неизвестными являются функции
– давления p px, y,z,t
– проекции скорости ux uxx, y,z,t, uy uyx, y,z,t, uz uzx, y,z,t
– и плотность (x, y,z,t)
всего пять неизвестных.
Для определения неизвестных используется система уравнений Эйлера. Поскольку число неизвестных превышает число уравнений, к системе добавляют уравнение неразрывности и уравнение состояния среды (зависимость плотности от давления).
Для несжимаемой жидкости уравнение состояния const и уравнение неразрывности
![]() ux
uy
uz
0
ux
uy
uz
0
x y z
Общего решения полученной системы уравнений нет, только частные решения для специальных задач.
1. Для элементарной струйки идеальной жидкости при установившемся движении
В качестве исходных возьмем дифференциальные уравнения движения идеальной жидкости Эйлера, умножим их соответственно на dx,dy,dz и сложим.
![]() 1 p dux *dx
1 p dux *dx
X
x dt
1 p duy
Y ![]() *dy
*dy
y dt
1 ![]() p duz *dz
p duz *dz
Z
z dt
![]()
![]() XdxYdy
Zdz
1 px dx
py dy
pz dz
dudtx dx dudty dy dudtz dz
XdxYdy
Zdz
1 px dx
py dy
pz dz
dudtx dx dudty dy dudtz dz
Произведем упрощение полученного выражения.
1. Полный дифференциал давления (движение установившееся)
p p p
![]() dp dx dy dz x y z
dp dx dy dz x y z
2. Преобразуем правую часть:
![]() dudtx dx dudty dy dudtz dz uxdux uyduy uzduz
d
dudtx dx dudty dy dudtz dz uxdux uyduy uzduz
d![]() ux2 u22y uz2
d
ux2 u22y uz2
d ![]() u22
u22
Окончательно получим:
1 u2
XdxYdy Zdz ![]() dpd
dpd ![]() 0
0
Первые три слагаемых называют полным дифференциалом силовой функции и обозначают dП Xdx Ydy Zdz .
1 u2
dП ![]() dpd
dpd ![]() 0
0
Рассмотрим частный случай. Из массовых сил действует только сила тяжести. Следовательно X Y 0 Z g .
1 u2
gdz ![]() dpd
dpd ![]() 0
0
Проинтегрируем и разделим на g :
2 p u
![]() z
C
z
C
g 2g
Для двух сечений элементарной струйки можно записать
|
2 2 z1 1 2u1g z2 pg2 2u2g p g |
Уравнение Бернулли для элементарной струйки идеальной жидкости в установившемся движении. |
Энергетически это выражает закон сохранения полной удельной (отнесенной к единице веса) энергии жидкости в элементарной струйке.
2. Для элементарной струйки вязкой жидкости в установившемся движении
При движении вязкой жидкости происходят потери энергии, которые должны быть учтены в уравнении Бернулли
2 2 z1 p1 u21g z2pg2 2u2g h12, g
где h12 – потери удельной энергии при перемещении из сечения 1 в сечение 2.
3. Для всего потока реальной жидкости
![]() Выделим в сечении
потока F элементарную
струйку
Выделим в сечении
потока F элементарную
струйку
( скорость u , сечение dF ).
Полная удельная энергия элементарной струйки в
2 p u
![]() данном
сечении e
z .
данном
сечении e
z .
Это удельная энергия, т.е. отнесенная к единице веса.
Если ее умножить на весовой расход через рассматриваемое сечение, то получим полую энергию, протекающую через поперечное сечение струйки в единицу времени dE Объемный расход dQ udF , весовой расход gdQ gudF . dE egudF
Полная энергия, протекающая в единицу времени через все сечение потока
E dE
F
Удельная энергия для всего сечения потока (полная энергия отнесена к весовому расходу)
E
Eуд ![]() .
.
gQ
Вычислим:
z p u2 udF
![]() Eуд
E
FegudF
F g 2g
Eуд
E
FegudF
F g 2g
gQ gQ Q
Замечания:
1. При установившемся движении плавно изменяющегося потока жидкости давление расp
пределяется
согласно гидростатическому закону, т.е. z ![]() const
g
const
g
2. По определению udF Q F
F
p u2 p 1 3 3
![]()
![]() Eуд
F
g udF
F
2g udF
Qz g
2g Fu dF
z
p 2
Fu3dF z
Eуд
F
g udF
F
2g udF
Qz g
2g Fu dF
z
p 2
Fu3dF z
2
p
![]() Окончательно
Eуд
z ,
Окончательно
Eуд
z ,
g 2g
3
u dF
![]() где
F
– коэффициент Кориолиса. Физический смысл: 3
где
F
– коэффициент Кориолиса. Физический смысл: 3
F
2 2
3 3 u u
![]()
Fu dF
Fu dF2 F
2 udF
F
2 dm
Eкинд
.
Fu dF
Fu dF2 F
2 udF
F
2 dm
Eкинд
.
3 3 2 m2 Eкинср
F F2 2 F 2
(здесь масса жидкости, проходящая за единицу времени через поперечное сечение элементарной струйки обозначена dm; всего потока – m )
Коэффициент Кориолиса есть отношение кинетической энергии, протекающей в единицу времени через поперечное сечение потока, при действительном распределении скоростей к такой же энергии, посчитанной по средней по сечению скорости.
Характеризует неравномерность распределения скоростей по сечению потока и равен: ламинарный режим 2
• турбулентный режим 1,051,15
• В практических расчетах обычно принимают 1.
4. Для всего потока вязкой жидкости
2 2
z1p1 12g1 z2pg2 22g2 hW12 g
hW12 – потери полной удельной энергии потока между сечениями 1 и 2 Эти по-
тери называются потери на трение и обозначаются hтр . Забегая вперед отметим, что в гидравлике потери на трение в потоке рассматриваются как сумма потерь на трение по длине трубы и потерь в местных сопротивлениях hтр hl hм.
Замечание о размерностях.
Слагаемые уравнения Бернулли имеют размерность длины (высоты) L. Они представляют собой энергию потока (потенциальную и кинетическую), отнесенную к единице веса жидкости, т.н. «удельную» энергию.
Вспомним последовательность вывода уравнения Бернулли. Величина Х – проекция на ось х плотности распределения равнодействующей массовых сил – имеет размерность ускорения, т.е. силы, отнесенной к единице массы. После умножения на dх (сила на путь) получили работу внешних сил (энергию), отнесенную к единице массы. При выводе разделили на g (ускорение свободного падения) и получили энергию, отнесенную к единице веса ( G mg ).
Сказанное означает, что если каждое слагаемое уравнения Бернулли умножить на вес mg , то получим ту или иную энергию элемента жидкости массы m .
1. Геометрическая высота z – измеряется по вертикали от плоскости сравнения до любой точки живого сечения потока (для определенности – до центра тяжести живого сечения). Очевидно mgz Eпот_z – потенциальная энергия положения.
Вывод : z – удельная потенциальная энергия положения. p
2.
Пьезометрическая высота ![]() – высота
поднятия жидкости в пьезометре. Измеряg
– высота
поднятия жидкости в пьезометре. Измеряg
ется от центра тяжести живого сечения до уровня воды в пьезометре. В лабораторных работах определяется непосредственно по шкале пьезометра, обычно проградуированного в см. При умножении на вес рассматриваемого объема жидкости, учиp
тывая m V , имеем: ![]() mg pV Eпот_p – потенциальная
энергия давления g
mg pV Eпот_p – потенциальная
энергия давления g
(работа вытеснения) p
Вывод : ![]() – удельная
потенциальная энергия давления.
– удельная
потенциальная энергия давления.
g
2
3. Скоростной напор ![]() .
Расчетная величина, определяемая по средней скорости 2g
.
Расчетная величина, определяемая по средней скорости 2g
![]()
![]() потока. При
умножении на вес рассматриваемого объема жидкости, учитывая физический смысл
коэффициента Кориолиса, имеем: 2 Eкинсрд
m22 Eкинд –
потока. При
умножении на вес рассматриваемого объема жидкости, учитывая физический смысл
коэффициента Кориолиса, имеем: 2 Eкинсрд
m22 Eкинд –
2g Eкин
кинетическая энергия рассматриваемого объема жидкости. Для элементарной
2 2 u mu
струйки аналогично ![]() mg
mg ![]() .
.
2
Вывод: ![]() –
удельная кинетическая энергия.
–
удельная кинетическая энергия.
2g
4. Потери hтр (h для элементарной струйки) измеряются в метрах (см, мм) и представляют собой потери удельной энергии при перемещении из одного сечения в другое.
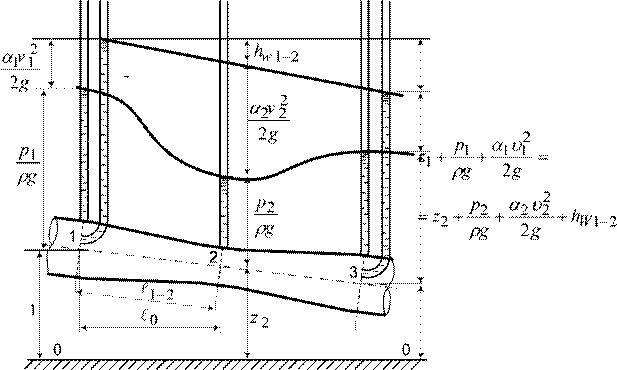 z
z
|
величина |
геометрически |
энергетически |
|
z |
геометрический напор = высота центра тяжести сечения от плоскости сравнения = образует геометрический уклон |
удельная потенциальная энер- гия положения (везде удельная это отнесенная к весу) |
|
p
g |
пьезометрическая высота = высота уровня жидкости в пьезометре от центра тяжести сечения |
удельная потенциальная энергия давления |
|
p z g |
пьезометрический напор = высота уровня жидкости в пьезометре от плоскости сравнения = образует пьезометрическую линию =образует пьезометрический уклон |
полная удельная потенциаль- ная энергия потока в данном сечении |
|
2
2g |
скоростной напор = на сколько полный напор выше пьезометрического |
удельная кинетическая энергия. |
|
|
= расстояние по вертикали между линией полного напора и пьезометрической линией =для равномерного течения постоянен, а линии параллельны |
Кинетическая энергия 2 m Eк 2 Вес G mg 2 Eк G 2g |
|
2 p 1
g 2g |
полный гидродинамический напор = уровень в трубке полного напора, отсчитанный от плоскости сравнения = образует линию полного напора = образует гидравлический уклон |
полная удельная энергия потока в данном сечении |
|
hW1-2 |
снижение линии полного напора при переходе от сечения 1 к сечению 2. Для идеальной жидкости линия полного напора горизонтальна |
Потери полной удельной энергии потока за счет вязкости (диссипация энергии) Складывается из потерь по длине и потерь в местных сопротивлениях hW1-2 hl hм |
Уклон это изменение величины по длине потока. Может быть определен в данном сечении или средний по длине.
Рассматриваем средние при переходе от сечения 1 к сечению 2 (знак не так, как в производной !).
Геометрический уклон (геодезический) – изменение геометрической высоты по длине потока
Jгеом z1 z2
l0
Пьезометрический уклон – изменение пьезометрической высоты по длине потока. Может менять знак.
p1z2 p2
Jпьез z1 g g
l12
Гидравлический уклон – изменение полного напора по длине потока. Не может быть отрицателен (потери не отрицательны). Для идеальной жидкости равен нулю.
z p1 112z2 p2 222
1 g 2g
J g 2g hW1-2 l12 l12
Правила написания уравнения Бернулли при решении задач.
1. Определить для элементарной струйки или для всего потока записывается уравнение.
2. Указать для идеальной или для вязкой жидкости записывается уравнение.
3. Выбрать и указать на чертеже два сечения, для которых записывается уравнение. Векторы местных скоростей в них должны быть параллельны.
4. Выбрать и обозначить на чертеже плоскость сравнения – горизонтальную плоскость, обычно совпадающую с центром тяжести ниже расположенного сечения.
5. Записать полную форму уравнения Бернулли и затем, если возможно, приравнять к нулю отдельные члены.
Напряжения в движущейся вязкой жидкости.
В невязкой жидкости действуют только нормальные напряжения.
При движении вязкой жидкости в ней возникают не только нормальные, но и касательные напряжения, так как вязкая жидкость обладает способностью оказывать сопротивление относительному сдвигу своих слоев.
Эти напряжения зависят не только от координат точки, но и от ориентации площадки действия.
![]() Рассмотрим элементарный параллелепипед с ребрами dx,dy,dz , выделенный в движущейся
жидкости.
Рассмотрим элементарный параллелепипед с ребрами dx,dy,dz , выделенный в движущейся
жидкости.
Обозначим сопротивления на гранях. Первый индекс – направление оси, к которой перпендикулярна данная грань. Второй индекс – направление действия напряжения. Считая напряжение непрерывными, используя разложение в ряд Тейлора, определим напряжения на гранях, удаленных от начала координат. На рисунке показаны только напряжения, действующие на левую и правую грани.
|
грань |
нормальное напряжение |
касательное напряжение |
|
|
левая |
pxx |
xy |
xz |
|
правая |
p
x |
xy xy
x |
x |
|
задняя |
pyy |
yx |
yz |
|
передняя |
pyy pyy y |
yx yx
y |
yz yz
y |
|
нижняя |
pzz |
zx |
zy |
|
верхняя |
p
z |
z |
zy zy
z |
Отметим без доказательства, что касательные напряжения на взаимно перпендикулярных площадках, направленные по нормали к линии пересечения этих площадок, равны друг другу:
xy yx , xz zx , yz zy
Составим уравнение движения массы жидкости, заключенной в элементарном параллелепипеде. Сумма сил, действующих на жидкую частицу, равна произведению ее массы на ускорение. Силы массовые и поверхностные. Сначала в проекции на ось X .
Проекция суммарной массовой силы на ось есть произведение плотности распределения равнодействующей массовых сил Х на массу частицы dxdydz . Хdxdydz
Поверхностные силы действуют на все шесть граней. Они равны произведению соответствующего напряжение (нормального или касательного) на площадь грани. Запишем только силы, проекция которых на ось х не равна нулю:
![]()
![]() pxx p
pxx p
Левая грань и правая: pxx dydz pxx dxdydz xx dxdydz
x x
yx yx
Задняя грань и передняя: yx dxdzyx
![]() y dydxdz
y dydxdz
![]() y dydxdz
y dydxdz
![]()
![]() Нижняя грань и верхняя: zx dxdyzx
zx dzdxdy
zx dzdxdy
Нижняя грань и верхняя: zx dxdyzx
zx dzdxdy
zx dzdxdy
z z
![]() dux
dux
Масса на ускорение: dxdydz dt
После сокращения и деления на массу получим
![]() X 1pxxx yyx zzx
dudtx
X 1pxxx yyx zzx
dudtx
Без доказательства укажем: В вязкой жидкости сумма нормальных напряжений по трем взаимно перпендикулярным граням не зависит от ориентации этих площадок. Введем понятие давления в движущейся жидкости, численно равное среднему нормальному напряжению
pxx
pyy
pzz p ![]()
3
Выразим нормальные напряжения на грань через давление и добавочное вязкое напряжение pxx p pxxв.
По закону Ньютона, распространяя его на пространственное движение, вязкое напряжение пропорционально
![]()
![]() pxxв 2ux yx
uyx uxy
xz
uzx
uxz
pxxв 2ux yx
uyx uxy
xz
uzx
uxz
x
Произведем необходимые подстановки. Упростим, используя уравнение неразрыв-
![]() ности
в дифференциальной форме ux
uy
uz
0.
ности
в дифференциальной форме ux
uy
uz
0.
x y z
![]() 1 p 2ux
2ux
2ux
dux
1 p 2ux
2ux
2ux
dux
X
x x2 y2 z2 dt
Учтем, что ![]()
v и по
аналогии запишем проекции на другие оси.
v и по
аналогии запишем проекции на другие оси.
1 p 2 2 2
X ![]() v
ux
ux
ux
dux
v
ux
ux
ux
dux
x x2 y2 z2 dt
1 p 2 2 2
Y ![]()
v
xu2y
yu2y
zuy
dudty
несжимаемой вязкой жидкостиУравнения Навьенеустановившегося движения -Стокса
для
v
xu2y
yu2y
zuy
dudty
несжимаемой вязкой жидкостиУравнения Навьенеустановившегося движения -Стокса
для
y 2
Z ![]()
1 p v2xu2z
2yu2z
2zu2z
dudtz
1 p v2xu2z
2yu2z
2zu2z
dudtz
z
2 2 2
![]() Упростим
запись, используя оператор Лапласа 2
Упростим
запись, используя оператор Лапласа 2
2 2 2
x y z
1 ![]() p 2 dux
p 2 dux
X
![]() x v ux
dt
x v ux
dt
Y
![]() 1 p v2uy
1 p v2uy
![]() duy y dt
duy y dt
Z ![]()
![]() 1 p v2uz
duz
1 p v2uz
duz
z dt
Субстанциальное ускорение в правой части можно раскрыть как сумму локального и
![]()
![]() конвективного dux
ux
ux ux
ux uy
ux uz ( аналогично по
другим осям). dt t x y z
конвективного dux
ux
ux ux
ux uy
ux uz ( аналогично по
другим осям). dt t x y z
Эти уравнения совместно с уравнением неразрывности и уравнением состояния образуют замкнутую систему, которая, однако, не имеет общих решений.
В основу гидродинамики как раздела гидромеханики положены четыре основных закона механики:
– закон сохранения массы
– закон изменения количества движения (импульса)
– закон изменения момента количества движения
– закон изменения кинетической энергии
Эти законы формулируются для объемов жидкости конечных размеров.
Закон сохранения массы. При движении жидкого объема его масса остается неизdm
менной. ![]()
0. Из этого
вытекают уравнения неразрывности в дифференциальной форме dt
0. Из этого
вытекают уравнения неразрывности в дифференциальной форме dt
и для потока жидкости.
Закон изменения количества движения. Изменение количества движения жидкого объема за единицу времени равно сумме всех приложенных к нему внешних (массовых и поверхностных) сил.
r r d(mr) r
В векторной форме d(m) Pdt или ![]()
P
P
dt
Закон изменения момента количества движения. Изменение момента количества движения жидкого объема относительно некоторой неподвижной точки за единицу времени равно сумме моментов всех внешних (массовых и поверхностных) сил, действующих на этот объем.
Закон изменения кинетической энергии. Изменение кинетической энергии жидкого объема за единицу времени равно мощности всех внешних и внутренних (поверхностных и массовых) сил, действующих на этот объем жидкости.
![]() Рассмотрим закон изменения количества движения
применительно к потоку жидкости.
Рассмотрим закон изменения количества движения
применительно к потоку жидкости.
Жидкость несжимаема : 1 2
Движение установившееся :
Q1 Q2
На выделенный объем действуют массовая сила веса, поверхностные силы давления P1 p1F1,
P2 rp2F2 и реакция стенок ка нала R .
За время dt жидкость из сечения 1 переместится в сечение 1`, а из сечения 2 в сечение 2`.
Изменение количества движения r r r r r r r r r
K K1'2' K12 (K1'2 K22')(K11' K1'2) K22' K11'
Изменение количества движения равно разности количества движения вышедшей массы и вошедшей массы.
Входящая масса dm1 dV1 F11dt Qdt
Выходящая масса dm2 dV2 F22 dt Qdt
Изменение количества движения за единицу времени:r r r
K dm11 dm22 Q(2 1)
Закон изменения количества движения
r r r r r
K P1 G P2 R
(При изображении многоугольника сил (см. рисунок) следует правильно выбирать их направления. Вес вниз, силы давления нормальны к сечениям и действуют внутрь объема, r r r r r r
K K22' K11' следовательно K K11' K22' , а направления векторов количества движения совпадают с направлениями скоростей, сила реакции обеспечивает поворот). r
Как правило неизвестной является реакция стенок канала R . Векторное уравнение решается обычно через проекции на оси координат.
Для измерения местных скоростей применяются гидродинамические трубки, термоанемометры и гидрометрические вертушки.
Определение скоростей с помощью
гидродинамических трубок основано на измерении скоростного напора u2![]() 2g , равного разности
полного Р2
2g , равного разности
полного Р2![]() g и статического напоров в
потоке. Полный напор измеряется трубкой полного напора, представляющей собой
изогнутую под прямым углом трубку, обращенную своим открытым концом против
потока.
g и статического напоров в
потоке. Полный напор измеряется трубкой полного напора, представляющей собой
изогнутую под прямым углом трубку, обращенную своим открытым концом против
потока.
![]() Из уравнения
Бернулли, записанного для 1 и 2-го сечения элементарной струйки следует
Из уравнения
Бернулли, записанного для 1 и 2-го сечения элементарной струйки следует
2
![]() откуда
u
pg2 pg12g
2gh
откуда
u
pg2 pg12g
2gh
Т
![]()
Трубка полного напора и
статического напора, конструктивно объединены в одном приборе и представляют
собой гидродинамическую трубку. Пито-Прандтля. Приемником полного давления Р2 Р1 u2![]() 2
является отверстие 1 осевого канала цилиндра, сообщающееся через трубку полного
напора 6, помещенную в державке, со штуцером 9. Для приема статического
давления Р1 на боковой поверхности
цилиндра выполнены канавки 7, закрытые кожухом 4 с прорезями 3.
2
является отверстие 1 осевого канала цилиндра, сообщающееся через трубку полного
напора 6, помещенную в державке, со штуцером 9. Для приема статического
давления Р1 на боковой поверхности
цилиндра выполнены канавки 7, закрытые кожухом 4 с прорезями 3.
Гидродинамическая трубка Пито-Прандтля со сферическим носком
Используются также гидродинамические трубки иного конструктивного оформления. Местная скорость (скорость в точке) определяется по формуле
![]() u
2gh ,
u
2gh ,
где - поправочный коэффициент, определяемый путем тарирования трубки.
Гидродинамические трубки применимы для измерения скоростей более 1 м/с.
Действие термоанемометров основано на использовании зависимости между электрическим сопротивлением проводников и их температурой. Термоанемометр представляет собой проволоку из инертного металла (платины, вольфрама, никеля), припаянную к двум электродам, закрепленным в державке (рисунок 6). Толщина проволоки 0,005-0,01 мм, длина 1-3 мм. Проволока помещается в поток и нагревается электрическим током. Поток, обтекающий проволоку, охлаждает ее, электрическое сопротивление проволоки при этом изменяется на некоторую величину в зависимости от скорости потока, фиксируя это изменение с помощью соответствующих электрических схем, можно определить величину местной скорости потока, нормальной к проволоке.
Схема электрической цепи и тарировочная кривая
термоанемометра, работающего по методу постоянной силы тока: u - скорость потока; V - напряжение тока
Гидродинамическая вертушка представляет собой лопастное колесо, помещенное в поток и приводимое им во вращение. В процессе измерения фиксируется скорость набегающего потока. Вертушка предварительно тарируется и снабжается тарировочным графиком u f h
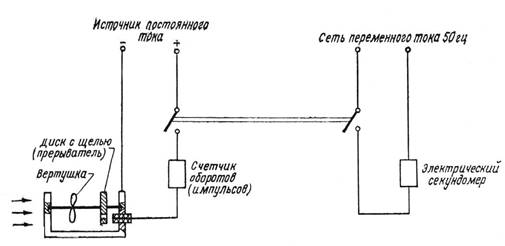
Средство измерения расхода или количества жидкости называется преобразователь расхода.
|
|
Расходомер |
Прибор, измеряющий мгновенный расход вещества (т.е. массу или объем вещества, протекающую через сечение в единицу времени |
|
|
Счетчик количества (или просто счетчик) |
Устройство, измеряющее массу или объем вещества, прошедшую по трубопроводу за определенный интервал времени (аналог – бытовые электросчетчики) |
|
|
Расходомер-счетчик
|
Устройство для измерения расхода и количества вещества |
По типу измеряемой среды различают расходомеры жидкостные, газа и пара. Одна и та же модель расходомера не может использоваться для измерения разных сред – слишком различны физические параметры.
Под жидкостью понимаются любые типы капельных жидкостей (вода, мазут, нефть и др. технические жидкости)
Под газом понимается природный (метан) или технический (кислород, водород и т.п.) газ, а также сжатый воздух.
Пар может использоваться сухой насыщенный или перегретый. Для влажного пара корректное измерение расхода невозможно. Особо оговариваются максимальные давление и температура пара.
• Объемные Измеряют объемный расход – таких подавляющее большинство
• Массовые Измеряют массовый расход непосредственно без пересчета по плотности (пример – кориолисовые)
• Объемно-массо- Массовый расход рассчитывается по измеренному объемному вые расходу через плотность жидкости, рассчитанную по давлению и температуре.
По выходному сигналу – с аналоговым, импульсным или цифровым выходом.
• мерные емкости (тарированный резервуар, бак)
• мерные водосливы (поплавковые расходомеры)
• с переменной площадью сечения – ротаметры
• переменного перепада давления – диафрагмы, сопла и трубы Вентури
• тахометрические
• электромагнитные (индукционные)
• ультразвуковые
• вихревые
• кориолисовые
При объемном способе измерения расхода жидкости, жидкость поступает в тщательно тарированный резервуар (мерник), при этом фиксируется время наполнения t определенного объема V . Объемный расход равен
V Q ![]() .
.
t
Способ измерения расхода с помощью мерного резервуара является наиболее точным. Он широко применяется в лабораторной практике для опытных исследований и поверок измерителей расхода.
Мерные водосливы служат для измерения расхода воды в лабораториях и на оросительных системах. Пример – треугольный водослив с тонкой стенкой в лабораторных работах.
![]() Ротаметр
представляет собой коническую прозрачную стеклянную трубку 1
Ротаметр
представляет собой коническую прозрачную стеклянную трубку 1
(угол конусности от 35 до 5о35// ) с помещенным внутри нее поплавком 2.
Ротаметр устанавливается на вертикальном участке трубопровода. Если сила, воздействующая на поплавок, превышает вес поплавка, то поплавок всплывает, увеличивая площадь щели для протекания жидкости, при этом сила, действующая на поплавок со стороны жидкости, уменьшается. Когда гидродинамическая сила становится равной весу поплавка, его всплывание прекращается.
Измерение расхода ротаметром основывается на использовании связи между расходом и положением поплавка. Характер этой связи зависит от угла конусности трубки, формы и веса поплавка, вязкости жидкости и обычно устанавливается путем индивидуального тарирования ротаметров.
Ротаметры применяют для измерения расходов жидкости и газа в широком диапазоне, начиная от малых, порядка 0,1 см3/с. Погрешность измерений не превышает 6 %. Недостатком их является зависимость показаний от физических свойств жидкости и невозможность измерять переменные во времени расходы.
Расходомерами переменного перепада давления называются измерительные комплексы, основанные на зависимости перепада давления, создаваемого устройством, установленным в трубопроводе, от расхода жидкости или газа. Состав комплекса:
1. Первичный преобразователь расхода (гидравлические сопротивление, трубка Пито); 2. Первичные линии связи – соединительные трубки и вспомогательные устройства на них (отстойные сосуды, воздухосборники);
3. Первичный измерительный прибор – дифманометр;
4. Вторичные линии связи (электрические провода)
5. Электронный преобразователь (записывающий, показывающий)
|
|
с сужающим устройством |
Стандартные – диафрагма, сопло, труба Вентури – не требуют индивидуальной градуировки. |
|
|
|
с гидравлическим сопротивлением |
Например – шариковая набивка |
|
|
|
с напорным устройством |
Принцип действия основан на измерении перепада давления, возникающего при переходе кинетической энергии в потенциальную. |
|
|
|
|
Пример – Трубка Пито-Прандтля или осредняющие напорные трубки, установленные поперек трубопровода |
|
|
|
центробежные расходомеры |
Основаны на зависимости расхода от перепада давления, образующегося на закругленном элементе трубопровода (колене) под действием центробежных сил |
|
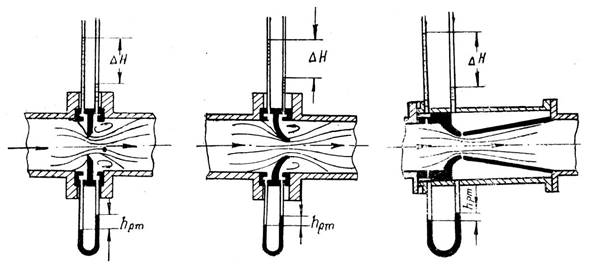
Расходомеры переменного перепада давления:
а – диафрагма; б – сопло; в – труба Вентури
Расход жидкости определяется по формуле
2p
![]()
![]() Q F 2gH или Q F
Q F 2gH или Q F
где - коэффициент расхода,
F - площадь проходного сечения сужающего устройства;
H - разность статических напоров,
. p - разность давлений до и после сужающего устройства
- плотность измеряемой среды (зависит от температуры и давления)
Скоростные счетчики чаще всего применяют для контроля количества воды, расходуемой в системах водоснабжения. Различают скоростные счетчики с вертикальной крыльчаткой (крыльчатые) и с винтовыми вертушками (турбинные).
Крыльчатый счетчик состоит (рисунок 9) из крыльчатки 1 и передаточного механизма 8, связанного со счетным механизмом 9. Передаточный и счетный механизм представляет собой ряд последовательно зацепленных шестерен.
Расход жидкости определяется отношением прошедшего через счетчик объема жидкости V за определенное время к времени t
V Q ![]() .
.
t
Ротаметр представляет собой коническую прозрачную стеклянную трубку 1 (угол конусности от 35 до 5о35// ) с помещенным внутри нее поплавком 2.
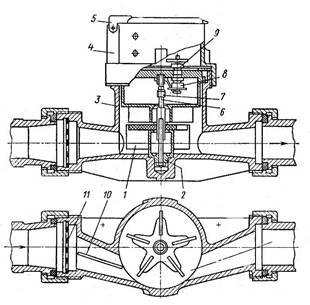
Счетчик с вертикальной крыльчаткой
Ротаметр устанавливается на вертикальном участке трубопровода. Если сила, воздействующая на поплавок, превышает вес поплавка, то поплавок всплывает, увеличивая площадь щели для протекания жидкости, при этом сила, действующая на поплавок со стороны жидкости, уменьшается. Когда гидродинамическая сила становится равной весу поплавка, его всплывание прекращается.
Измерение расхода ротаметром основывается на использовании связи между расходом и положением поплавка. Характер этой связи зависит от угла конусности трубки, формы и веса поплавка, вязкости жидкости и обычно устанавливается путем индивидуального тарирования ротаметров.
Ротаметры применяют для измерения расходов жидкости и газа в широком диапазоне, начиная от малых, порядка 0,1 см3/с. Погрешность измерений не превышает 6 %. Недостатком их является зависимость показаний от физических свойств жидкости и невозможность измерять переменные во времени расходы.
Тема 1.3. Движение реальных жидкостей
![]() Рассмотрим
трубопровод, состоящий из нескольких прямых участков постоянного диаметра и
местных сопротивлений: обратного клапана, задвижки и двух плавных поворотов на
90.
Рассмотрим
трубопровод, состоящий из нескольких прямых участков постоянного диаметра и
местных сопротивлений: обратного клапана, задвижки и двух плавных поворотов на
90.
Для сечений 1-1 и 2-2 потока может быть записано уравнение Бернулли, из которого выразим потери полного напора:
hW12 z1 pg1 21g12 z1 p2 22g22 .
g
Это общие потери от сечения 1-1 до сечения 2-2 , которые могут рассматриваться как сумма потерь по длине прямолинейных участков постоянного диаметра и потерь в местных сопротивлениях.
hW12 hl12 hм
Такое разделение – основное допущение при расчете потерь в трубопроводах.
Забегая вперед, отметим, что эти два типа потерь рассчитываются отдельно.
Потери по длине по экспериментальной формуле Дарси-Вейсбаха[6]
2 l
hl d ![]() 2g ,
2g ,
здесь – коэффициент гидравлического сопротивления (коэффициент Дарси).
Потери в местных сопротивлениях есть сумма отдельных потерь, каждая из которых вычисляется по формуле Вейсбаха:
n 2
hм
i
![]() 2g ,
2g ,
i1
здесь i – коэффициент местного сопротивления номер i , определяется из справочников.
(– «дзета», греч. не путать – «кси», греч.)
Местные сопротивления – места потока, в которых происходит резкая его деформация, скорость изменяется по величине и по направлению.
Для того чтобы измерить потери напора в местном сопротивлении поступают так:
1. производят замер потерь напора h1на местном сопротивлении, причем пьезометры устанавливают не рядом с ним, а на расстоянии не менее 10d , где поток невозмущенный.
2. производят замер потерь h2 на участке того же трубопровода длиной Ll без местного сопротивления
3. вычисляют hм h1 h2
![]()
Учитывая, что hм 2g , находят коэффициент местного сопротивления
2g
hм ![]() 2
2
Такой способ замера позволяет выделить отдельно влияние местного сопротивления.
Расчетным путем найти коэффициент местного сопротивления не удается, единственное исключение – внезапное расширение потока.
![]() Рассмотрим внезапное расширение круглого трубопровода,
выделим сечения 1-1 и 2-2.
Рассмотрим внезапное расширение круглого трубопровода,
выделим сечения 1-1 и 2-2.
Площади живых сечений потока F1 и
F2 , скорости 1 и 2.
Составим уравнение Бернулли для сечений 3-3 и 2-2, принимая скорость потока в сечении 3-3 равной 1 и учитывая, что z1 z2 0.
2 2
p1 21g1 pg2 22g2 hв.р g
здесь hв.р– потери напора на внезапном расширении.
2 2
Принимаем 1 2 1, находим потери hв.р g 2g
Применим к массе жидкости, заключенной между сечениями 3-3 и 2-2 теорему о количестве движения, согласно которой изменение количества движения в единицу времени равно сумме внешних сил. Допускаем, что во всем сечении 3-3 действует давление p1.
F222 1 p1 p2F2
Отсюда выразим
p1 p2 2(2 1) и подставим в выражение для потерь
g g
![]() hв.р
2(21) 122g22
2222221g1222
(12g2)2
hв.р
2(21) 122g22
2222221g1222
(12g2)2
g
2 Формула Борда: потери напора при внезап-
![]() hв.р 1 2g2) ном расширении потока пропорциональны квадрату «потерянной»
скорости[7].
hв.р 1 2g2) ном расширении потока пропорциональны квадрату «потерянной»
скорости[7].
Приведем это выражение к виду формулы Вейсбаха для местных сопротивлений:
2 2 2
hв.р 21 112 121g
g
По уравнению неразрывности для потока 1F1 2F2 т.е.
1 F2
2
Коэффициент сопротивления (отнесенный к скорости до расширения) 1 1 F2
В предельном случае, когда F2 F1, имеем выход из трубопровода в резервуар больших размеров, вых 1.
Так как скорость до расширения 1 не равна скорости после него 2 , то для данного местного сопротивления существует два различных значения коэффициента сопротивления, расчет потерь напора с использованием которых, разумеется, приводит к одинаковому результату. 2 2 2
1 hв.р 12g 222g . Легко показать, что 2 FF12 1
![]() Плавный поворот потока
Плавный поворот потока
При изменении направления потока появляются центробежные силы, направленные от центра кривизны к внешней стенке трубы.
Давление в пределах поворота у внешней стенки больше, чем у внутренней. Соответственно скорости у внешней стенки меньше, чем у внутренней. Вследствие этого вдоль боковых стенок трубы, вблизи поверхности которых скорость невелика, будет происходить движение жидкости от внешней циркуляция в потоке. стенки к внутренней, т.е. возникает поперечная
В результате образуется так называемый парный (двойной) вихрь, который накладывается на поступательное движение. Линии тока становятся винтообразными. Эпюра скоростей в связи с этим перестраивается.
Если местные сопротивления расположены на близком расстоянии друг от друга, то они влияют друг на друга.
![]() Так например, при
последовательном соединении двух отводов (отвод-поворот на 90о,
рисунок VI-2) суммарный коэффициент сопротивления в случае а) сум 1,490, а в случае б) сум
390
Так например, при
последовательном соединении двух отводов (отвод-поворот на 90о,
рисунок VI-2) суммарный коэффициент сопротивления в случае а) сум 1,490, а в случае б) сум
390
Здесь 90 – коэффициент сопротивления изолированного поворота на 90, зависит от отношения радиуса поворота R к диаметру трубопровода d . В справочниках приводятся коэффициенты сопротивления для отвода без учета потерь по длине трубы, которые рассчитываются дополнительно, причем длина считается по средней линии потока.
где d – диаметр трубопровода; м.кв– коэффициент потерь для данного местного
сопротивления в квадратичной области; – коэффициент Дарси.
В обычных условиях длина прямолинейного участка трубопровода между сопротивлениями, равная 10d , оказывается достаточной для стабилизации потока. В ответственных случаях, например при установке расходомерных устройств, эта длина определяется правилами установки и составляет (12 20)d .
Эквивалентная длина. Для упрощения расчета трубопроводов часто используют понятие о эквивалентной длине местного сопротивления, т.е. об участке данного трубопровода такой длины, на которой потери напора по длине равны местной потере напора:
2 lэкв 2 l
hм hдл.экв => м![]() 2g
d
2g
d ![]() 2g => эквd м
2g => эквd м
В гидравлически длинных трубопроводах (или просто длинных) потери по длине настолько превышают потери в местных сопротивлениях, что последние не вычисляют, а принимают как некоторую часть потерь по длине (добавляют 5 % – 10 %).
![]() Рассмотрим установившее напорное движение несжимаемой
жидкости в трубе круглого сечения постоянного диаметра.
Рассмотрим установившее напорное движение несжимаемой
жидкости в трубе круглого сечения постоянного диаметра.
Из постоянства диаметра следует:
F1 F2 F .
Средняя скорость потока по определению есть отношение объемного расхода к площади живого сечения. Расход в рассматриваемых сечениях одинаков, значит 1 2 . z1 и z2 – ординаты центров тяжести выделенных сечений, отсчитанные от плоскости сравнения.
Запишем уравнение Бернулли для сечений 1-1 и 2-2 потока вязкой жидкости: Плоскость сравнения обозначена на чертеже 0-0.
2 2
z1 p1 11 z2 p2 22 hl
g 2g g 2g
Допустим, что распределение скоростей в сечениях одинаково (1 2 ), тогда :
z p1 z2 pg2 hl (см. рисунок)
1 g
Сумма действующих на выделенный объем сил равна произведению его массы на ускорение. В данном случае жидкость движется без ускорения, значит сумма сил, действующих на выделенный объем, равна нулю.
На объем жидкости между сечениями 1-1 и 2-2 действуют:
массовые силы – сила веса G gV g Fl поверхностные силы:
– давления слева P1 p1F
– давления справа P2 p2F
– силы нормального давления стенок (взаимно уравновешиваются)
– сила вязкого трения, обусловленная касательными напряжениями 0 , действующими на площади Fтр l (длина участка трубы умноженная на смоченный периметр)
Сумма сил в проекции на ось трубы равна нулю: Gcos P1 P2 0Fтр 0
Здесь 0 – касательное напряжение между неподвижным слоем на стенке (гипотеза прилипания) и соседним подвижным слоем.
z
Подставим выражения для сил. Из чертежа очевидно cos 1 z 2
l
g Fz1 z2 p1F p2F 0l 0 Разделим на g F и сгруппируем:
![]()
![]() z1 p1
z 2 p2 0
z1 p1
z 2 p2 0 ![]()
l
l
g g F g
Заметим, что разность в левой части полученного выражения по уравнению Бернулли = hl
.
F l
Учтем, что по определению Rг ![]() , g получим hl 0
, g получим hl 0 ![]()
Rг
Гидравлический уклон J hl . Окончательно
l
|
0 Rг J |
Основное уравнение равномерного движения (как ламинарного, так и турбулентного) |
Распределение касательных напряжений по толщине потока.
![]() В движущемся потоке
радиуса r
выделим цилиндрический объем радиуса y , y r
В движущемся потоке
радиуса r
выделим цилиндрический объем радиуса y , y r
Применим к выделенному объему основное уравнение движения.
Гидравлический радиус для круглого потока равен половине (!) геометрического радиуса. y
2
![]() Следовательно
распределение касательных напряжений по радиусу потока линейное,
Следовательно
распределение касательных напряжений по радиусу потока линейное,
на оси потока y 0 и 0, у стенки y r и 0
Повторим: Полученные выводы справедливы для любого равномерного движения, как для ламинарного, так и для турбулентного.
1.3.3. Режимы движения жидкости. Опыты Рейнольдса[8]. Число Рейнольдса.
Многочисленные экспериментальные исследования показали, что потери энергии при движении жидкости существенно зависят от особенностей движения частиц жидкости в потоке, от режима движения.
Наглядно особенности режимов движения можно наблюдать на специальной опытной установке, схема которой показана на рисунке
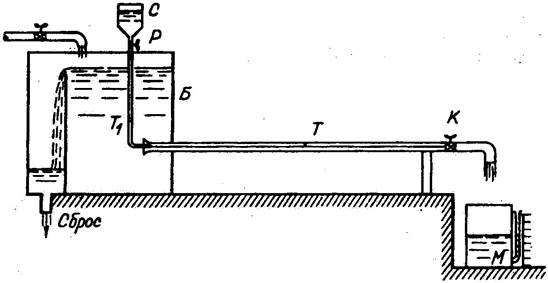
К баку достаточно больших размеров, наполненному жидкостью, присоединена стеклянная труба Т ; вход в трубу сделан плавным; в конце трубы установлен кран К для регулирования расхода потока. Расход измеряют с помощью мерного бака М и секундомера.
Над баком расположен сосуд С, наполненный раствором краски, плотность которой близка к плотности жидкости в потоке. По тонкой трубке Т1 краска водится в жидкость, движущуюся по трубе Т . Расход краски регулируется краном Р.
При открытом кране К в трубе Т установится некоторая скорость потока (высота уровня жидкости в баке поддерживается постоянной). Если открыть кран Р, то в трубу Т начнет поступать краска. При малой скорости потока v в трубе Т краска образует прямолинейную и резко выделяющуюся, не смешивающуюся с окружающей жидкостью струйку. Заметного обмена частицами между окрашенной струйкой и окружающей ее жидкостью не происходит. Если ввести в жидкость краску несколькими струйками, все они будут двигаться не смешиваясь с остальной массой жидкости. Это свидетельствует о том, что в прямой стеклянной трубе Т при данном открытии крана жидкость движется отдельными, не перемешивающимися между собой слоями. Линии тока при этом прямолинейны и устойчивы. Это ламинарное движение (от латинского lamina – слой).
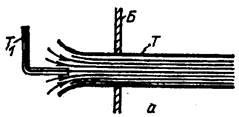
Ламинарный режим движения – частицы жидкости движутся параллельными слоями, не перемешиваясь.
При некотором большем открытии крана (увеличении скорости ) окрашенная струйка начинает искривляться и становится волнообразной. Это может происходить только в результате изменений во времени (пульсаций) векторов местных скоростей в потоке. Такой режим называется переходным.
При дальнейшем увеличении скорости потока в трубе Т струйка распадается на отдельные хорошо видные вихри, окрашенные струйки перемешиваются со всей массой текущей жидкости. Это турбулентное (от латинского turbulentus – беспорядочный) движение.
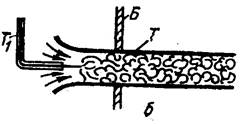
Турбулентный режим движения – в потоке существуют пульсации местных скоростей, давлений и касательных напряжений, приводящие к хаотическому, беспорядочному движению частиц и перемешиванию.
При постепенном закрытии крана явление повторяется в обратном порядке. Однако переход от турбулентного режима к ламинарному происходит при скорости меньше той, при которой произошел переход от ламинарного режима к турбулентному.
Критическая скорость потока – при которой меняется режим движения. При этом имеют место две критические скорости: верхняя – vкр.в., которая соответствует смене ламинарного режима турбулентным, и нижняя – vкр.н., при которой происходит смена турбулентного режима ламинарным. при чем всегда vкр.н. vкр.в. В интервале между этими скоростями режим движения может быть и ламинарный и турбулентный, эта зона называется переходной. В переходной зоне ламинарный режим неустойчив и легко переходит в турбулентный. Для оценки состояния потока выбрана нижняя критическая скорость, при ней и при меньших скоростях режим всегда ламинарный. Опытами Рейнольдса было установлено, что нижняя критическая скорость для потока в круглой трубе пропорциональна кинематической вязкости v и обратно пропорциональна диаметру трубыd :
кр.н. kv/d . Коэффициент пропорциональности k оказался одинаковым для различных
v и d : k кр.н.d /v 2320. В честь Рейнольдса этот коэффициент был назван критическим числом Рейнольдса и обозначен Reкр. Верхней критической скорости соответ-
ствует Re 4000, однако это значение существенно зависит от условий опыта.
![]()
Скорость 0 ß vкр.н. ß à vкр.в.à
|
Ламинарный режим |
возможен, устойчив |
возможен, неустойчив |
невозможен |
|
Турбулентный режим |
невозможен |
возможен, устойчив |
возможен, устойчив |
Число Re 0 2320 4000
![]()
В общем случае режим движения жидкости определяется безразмерным комплексом
l l
![]() Re .
Этот комплекс называют числом Рейнольдса и обозначают Re.
Re .
Этот комплекс называют числом Рейнольдса и обозначают Re.
/ v
Число Рейнольдса – критерий подобия при доминирующих силах инерции.
Число Рейнольдса характеризует отношение сил инерции к силам трения (вязкости).
2 2 2 , а силы вязкого трения Силы инерции имеют порядок: Fин ma V l /t l
2 2
![]()
![]()
2 Fин l
lRe , где l – характерный
2 Fин l
lRe , где l – характерный
Fтр F l vl. Тогда
l Fтр vl v
поперечный размер живого сечения. При выводе учтено, что динамическая вязкость
3 2.
v, объем V l , скорость l /t, ускорение a l/t
Поскольку характерный размер живого сечения выбирают произвольно, то число Рейнольдса имеет индекс, указывающий выбранную характерную линейную величину. Чаще всего в качестве характерный линейных величин принимают диаметр трубы d или гидравлический радиус Rг или глубину жидкости в открытом русле (канале) h .
Тогда Red d /v; ReRг Rг /v; Reh h/v . Число Red обычно обозначают без индекса Re. В расчетах для цилиндрических круглых труб обычно принимают Reкр 2320. Для открытых русел ReкрRг 580, так как Rг d /4.
Определив число Рейнольдса для любого потока и сравнив его с критическим, можно узнать характер движения, который, в свою очередь, определяет зависимость потерь напора от скорости. В общем случае потери напора hl kn , где k – некоторый постоянный коэффициент. В случае ламинарного режима n1, т. е. потери пропорциональны скорости. При турбулентном режиме n 1.752.0в зависимости от степени турбулентности потока. При развитом турбулентном режиме потери напора пропорциональны квадрату средней скорости.
В природе и технике турбулентное движение наблюдается чаще, чем ламинарное. Области ламинарного движения – движение вязких жидкостей типа масел по трубам и в механизмах, движение грунтовых вод, движение в капиллярах (в том числе и движение крови в организмах).
Рассмотрим распределение скоростей по сечению и потери напора по длине трубы при установившемся ламинарном движении.
Движение равномерное, следовательно эпюра скоростей постоянная по длине трубы. Дополнительное условие: движение изотермическое, то есть температура не меняется, а значит плотность и вязкость тоже.
Режим ламинарный (определение было ранее: слоистое движение без перемешивания, Re≤2320).
Выделим цилиндрический объем движущейся жидкости радиусом y и применим к нему основное уравнение равномерного движения жидкости
Rг J здесь – касательное напряжение
![]() y hl –
гидравлический уклон
y hl –
гидравлический уклон
Rг – гидравлический радиус , J
2 l
du
По закону Ньютона , минус потому, что производная отрицательна, т.е. dy
вдоль оси y скорость падает, а всегда>0.
du y gJ
![]() J => ( v ; g ) => du
J => ( v ; g ) => du
![]() ydy dy 2 2v интегрируем:
ydy dy 2 2v интегрируем:
gJ 2
u
![]() y C
y C
4v
Постоянную интегрирования Cнаходим из условия, что на стенке при y r имеем
u 0 (гипотеза прилипания): C
![]() gJ r2 4v
gJ r2 4v
Окончательно u gJ (r2 y2) распределение скоростей по сечению в ламинарном режиме
![]()
4v
Это парабола, максимум при y 0 максимальная скорость umax
![]() 4v r2 16
4v r2 16![]() gJv d2 gJ
gJv d2 gJ
Найдем расход жидкости
![]() Рассмотрим
концентрический слой жидкости радиуса y толщиной dy
Рассмотрим
концентрический слой жидкости радиуса y толщиной dy
Расход через этот слой dQ udF , где dF 2ydy dQ ![]() gJ r2 y22ydy 4v
gJ r2 y22ydy 4v
Интегрируем по всему сечению по y
![]() Q
Q ![]() gJ 0r
r2 y2ydy2gJv
r24 r44
8gJv r4
gJ 0r
r2 y2ydy2gJv
r24 r44
8gJv r4
2v
4
![]()
![]() d => r4 d
d => r4 d
Учитывая, что r
2 16
gJ 4
Q ![]() d
d
Заметим: расход в ламинарном режиме при заданном гидравлическом уклоне J пропорционален четвертой степени диаметра.
Найдем среднюю скорость
Q
Средняя скорость (по определению
отношение объемного расхода к площади) ![]()
F
![]()
![]() gJ 4 4 gJ 2
Учитывая d2
4r2, получим
gJ r2
gJ 4 4 gJ 2
Учитывая d2
4r2, получим
gJ r2
d d
128v d2 32v 8v
Средняя скорость ровно в два раза меньше максимальной, макс
![]() gJ r2 , 4v
gJ r2 , 4v
макс .
2
Коэффициент Кориолиса для ламинарного режима движения
3
u dF
3
F
Найдем потери напора по длине трубы
Из выражения для средней скорости выразим гидравлический уклон
![]()
![]() gJ 2 => J 32v
gJ 2 => J 32v
32v d d2g
С другой стороны гидравлический уклон (по определению) J hl , следовательно:
l
32vl
![]() hl
2 формула Пуазейля[9]
d g
hl
2 формула Пуазейля[9]
d g
Из формулы видно: потери напора по длине трубы пропорциональны средней скорости потока в первой степени.
Для определения потерь напора по длине трубы обычно используется формула Дарси
2 l
hl
![]() ,
где
– коэффициент сопротивления Дарси d 2g
,
где
– коэффициент сопротивления Дарси d 2g
Чтобы найти коэффициент Дарси используем только что полученную формулу Пуазейля
2 32vl 64v d l
![]()
Отсюда
Отсюда ![]() .
Заметим, что Re
.
Заметим, что Re ![]() d 2g d2g d v
d 2g d2g d v
Получим: в ламинарном режиме
коэффициент Дарси ![]()
Замечание. Формула Дарси справедлива в ламинарном режиме, однако это не означает, что потери напора в этом случае пропорциональны квадрату скорости. Сам коэффициент Дарси пропорционален скорости в степени минус один (скорость входит в число Re). Следовательно, как и утверждалось ранее, потери напора по длине трубы при ламинарном режиме движения пропорциональны средней скорости потока в первой степени.
Начальный участок течения – участок от начала трубы, на котором формируется параболический профиль скоростей. За пределами этого участка имеем стабилизированное ламинарное течение, параболический профиль скоростей остается неизменным, как бы ни была длинна труба, при условии сохранения ее прямолинейности и постоянства сечения.
Длина начального участка – расстояние от входа в трубопровод до сечения, в котором скорость распределена по параболическому закону с точностью 1%.
lнач (0,030,04)d Re lнач.макс 60d
Потери на начальном участке больше примерно на 9%
du
Происходит
стабилизация профиля скоростей, а производные ![]() выше, чем в
основdy
выше, чем в
основdy
ном участке трубы. В практических расчетах увеличением потерь на начальном участке обычно пренебрегают, однако учитывают потери на вход из бака в трубу вх 0,5.
Рассмотрим плоский зазор между неподвижными пластинами.
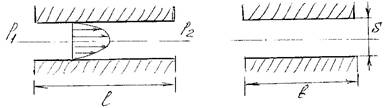
Толщина (величина) зазора s , длина зазора по направлению движения жидкости l , ширина зазора b. Жидкость движется через зазор под действием перепада давления p p1 p2. Полагаем, что течение установившееся и изотермическое (температура жидкости не меняется) и вязкость жидкости постоянна.
![]() Рассмотрим малый слой жидкости высотой 2y , расположенный
симметрично по центру зазора.
Рассмотрим малый слой жидкости высотой 2y , расположенный
симметрично по центру зазора.
На этот слой действуют тормозящие касательное напряжение, по закону Ньютона:
du du
, здесь – динамическая вязкость жидкости, ![]() –
градиент скорости dy dy
–
градиент скорости dy dy
слоистого движения в направлении оси y , величина отрицательная, т.к. скорость местная скорость потока u уменьшается при увеличении y , поэтому в формуле знак минус.
Запишем основное уравнение равномерного движения для выделенного фрагмента:
RгJ , где – касательное напряжение;
F 2by
![]() Rг – гидравлический
радиус, по определению Rг
2b
4y , т.к. y
b , то
Rг – гидравлический
радиус, по определению Rг
2b
4y , т.к. y
b , то
Rг y;
![]() hl .
hl .
J – гидравлический уклон, по определению J
l
du J
Приравняем
выражения для :
yJ , откуда du
![]() ydy dy
ydy dy
Интегрируем u ![]() J y2 C
J y2 C
2
Для нахождения постоянной интегрирования воспользуемся граничным условием,
2 s J s
вытекающим из гипотезы прилипания : при y ![]() имеем u
0, откуда C
имеем u
0, откуда C ![]()
2 2 4
Скорость при движении в щели
J 2
![]() u
s
y2
u
s
y2
2 4
2
Js
Это уравнение параболы, скорость максимальна при y 0: uмакс
![]() 8
8
![]() Для определения
расхода жидкости через щель выделим в ней элементарный слой толщиной dy , отстоящий от оси
потока на
Для определения
расхода жидкости через щель выделим в ней элементарный слой толщиной dy , отстоящий от оси
потока на
расстояние y .
![]() J
s2
y2
, расход
J
s2
y2
, расход
Площадь выделенного слоя dF bdy , скорость u
![]() dQ udF
J
s2
y2 bdy
dQ udF
J
s2
y2 bdy
2 4
Проинтегрируем по всему потоку, вследствие симметрии потока при интегрировании s
от 0 до ![]() результат нужно удвоить.
результат нужно удвоить.
2
s/2 2
![]()
![]() Q dQ 2 2J
s4 y2 bdy
Jb
s83 24s3
12Jb s3 F 0
Q dQ 2 2J
s4 y2 bdy
Jb
s83 24s3
12Jb s3 F 0
![]() Вспомним,
что J
hl и hl
p
Вспомним,
что J
hl и hl
p
l
Расход через узкую щель Q ![]() pb s3
pb s3
12l
Замечание: утечки через зазор пропорциональны ширине в третье степени, т.е. при увеличении зазора в 2 раза утечки возрастают в 8 раз.
![]() Утечки через зазор в поршневой паре
Утечки через зазор в поршневой паре
(диаметр поршня d , величина зазора s )
pd 3 Qут
![]() 12l s
12l s
При несимметричном расположении поршня в зазоре (при наличии эксцентриситета) расход увеличивается и при максимальном эксцентриситете Qмакс 2,5Qут.
![]() Измерение местных
скоростей турбулентного потока показали, что поле скоростей такого потока
изменяется беспорядочно, хаотично, однако изменение местных скоростей имеет
ярко выраженный пульсационный характер – значения составляющих скорости пульсируют
около некоторых осредненных значений. u – местная скорость, ux ,uy ,uz – ее про-
Измерение местных
скоростей турбулентного потока показали, что поле скоростей такого потока
изменяется беспорядочно, хаотично, однако изменение местных скоростей имеет
ярко выраженный пульсационный характер – значения составляющих скорости пульсируют
около некоторых осредненных значений. u – местная скорость, ux ,uy ,uz – ее про-
екции на оси координат.
r r r r r r
u uxi uy j uzk , где i , j,k – еди-
ничные векторы, направленные по осям ко-
Местная скорость меняется по величине и направлению, а ее проекции по величине и знаку около некоторого среднего значения.
Проекция скорости – функция времени ux ux(t)
Таким образом турбулентное движение является по самой своей природе движением типично неустановившимся. Изменение скорости имеет вид случайных беспорядочных отклонений. Однако несмотря на кажущуюся беспорядочность, среднее значение за достаточно длительный промежуток времени остается все-таки постоянным и не зависит от времени.
![]()
За осредненную скорость ux в данной точке принимается такая постоянная за период осреднения T скорость, при которой через элементарную площадку d за период T проходит объем жидкости, равный истинному ее объему, проходящему через d за время T , т.е.
T T
![]()
![]()
duxT dux dt , откуда uxT ux dt
0 0
Предполагается, что период осреднения T достаточно велик, так что осредненное значение не изменится, если выполнить повторное осреднение.
Мгновенные значения параметров турбулентного режима принято рассматривать в виде суммы осредненных (во времени) значений и пульсационных составляющих.
![]()
![]()
![]() Договоримся осредненные
параметры обозначать с чертой, пульсационные – со штрихом. При этом мгновенные
значения скорости и напряжений запишутся в виде ux ux ux , uy
uy uy , uz
uz uz
Договоримся осредненные
параметры обозначать с чертой, пульсационные – со штрихом. При этом мгновенные
значения скорости и напряжений запишутся в виде ux ux ux , uy
uy uy , uz
uz uz
p p p,
Необходимо различать осредненную скорость u (по времени, в данной точке) и сред-
![]() Q
Q
нюю скорость в данном живом сечении потока .
F
Пульсационные составляющие скоростей характеризуются амплитудой и частотой.
Заметим, что величина осредненной пульсационной составляющей всегда равна нулю.
![]() Для оценки степени пульсаций
используют среднее квадратичное отклонение пульсационных добавок ux
ux2 (корень из осредненного
значения квадрата пульсационной составляющей)
Для оценки степени пульсаций
используют среднее квадратичное отклонение пульсационных добавок ux
ux2 (корень из осредненного
значения квадрата пульсационной составляющей)
![]() 13(ux)2 (uy)2 (uz)2
13(ux)2 (uy)2 (uz)2
Степень турбулентности потока
u
2 2 2 осредненная местная скорость.
![]() где
u
ux uy uz
где
u
ux uy uz
Основной особенностью турбулентного потока является интенсивное перемешивание частиц жидкости. Отметим, что имеется в виду именно перемешивание частиц, а не молекул. Интенсивность перемешивания расчет с ростом Re.
Рассмотрим поток жидкости в прямолинейной цилиндрической трубе круглого сечения (осесимметричный поток). Структуру потока в трубе представим в виде приближенной двухслойной схемы (модели).
u 0 ламинарная пленка
![]() л На
твердой стенке (внутренняя поверх-ность трубы) скорости равны нулю.
л На
твердой стенке (внутренняя поверх-ность трубы) скорости равны нулю.
Вблизи твердой стенки находится очень тонкий слой л , в котором преимущественное значение имеют силы
uвязкого трения, рассчитываемые по за-
кону Ньютона, и жидкость движется без перемешивания.
Эта область называется вязкий под-
турбулентное ядро слой потока.
В пределах вязкого подслоя скорость линейно увеличивается от нуля на стенке до некоторого значения uв
30d
Толщина вязкого подслоя (без вывода) вп
При увеличении Re толщина вязкого подслоя уменьшается.
1.3.8. Возникновение дополнительных касательных напряжений. Теория турбулентности Прандтля.
Теория турбулентности Л. Прандтля, предложенная в 1925 г., основана на том, что количество движения массы, переносимой в потоке за счет поперечной пульсационной составляющей скорости, остается неизменным на некотором пути, а затем изменяется скачком. Длина этого пути l – так называемая длина пути перемешивания. Предполагается, что это расстояние моль жидкости проходит без взаимодействия с другими молями и сохраняя постоянным свое осредненное количество движения. После прохождения этого пути моль жидкости смешивается с жидкостью другого слоя, отдавая ей разницу количества движения.
![]()
![]()
![]() Рассмотрим
простейший случай плоскопараллельного осредненного турбулентного потока. Так
как поток принят пло-
Рассмотрим
простейший случай плоскопараллельного осредненного турбулентного потока. Так
как поток принят пло-
скопараллельным, то очевидно u y =0.
Покажем, что в таком потоке за счет пульсаций скоростей будет возникать дополни-
![]()
тельное касательное напряжение, равное ux uy , где ux uy – осредненное значение произведения пульсаций скорости по осям.
Рассмотрим два соседних слоя жидкости, разделенных площадкой . Пусть вблизи верхней площадки имеют место пульсации скоростей ux и uy . В этом случае можно сказать, что верхний слой движется относительно нижнего с какой-то относительной скоростью ux .
Под действием вертикальной пульсации скорости uy через площадку за время t протечет масса жидкости m uy t .
Верхнем слое эта масса приобретет ускорение в направлении оси x . При ускорении этой поступающей снизу массы верхний слой затормаживается. Этот эффект торможения равносилен приложению к верхнему слою на поверхности раздела слоев по площадке не которой касательной силы инерции T , направленной противоположно движению, или касательного напряжения . Эту силу можно легко подсчитать.
Изменение количества движения жидкости, прошедшей из нижнего слоя в верхний,
![]()
будет mux ux mux mux uxuyt.
Это изменение количества движения равно импульсу касательной силы T
T t uxuyt
Знак минус поставлен потому, что сила инерции всегда направлена против ускорения.
T
Учитывая, что ![]() получим
uxuy или осредненное за
период T :
получим
uxuy или осредненное за
период T :
![]()
ux uy .
Это и есть выражение для турбулентного касательного напряжения в функции от пульсационных скоростей.
![]()
![]() Величина
по закону независимости действия сил и напряжений должна быть добавлена к тому
чисто вязкому напряжению, которое действует между слоями турбулентного в
среднем установившегося потока
Величина
по закону независимости действия сил и напряжений должна быть добавлена к тому
чисто вязкому напряжению, которое действует между слоями турбулентного в
среднем установившегося потока ![]() dux
dux
лам турб uy ux .
dy
Придадим уравнению для касательного напряжения такой вид, чтобы дополнитель-
![]()
ные напряжения турб uy ux были выражены не через пульсационные составляющие скорости, а через осредненные значения.
![]()
Рассмотрим два слоя жидкости. Первый слой движется со скоростью ux , второй
ux
![]() находится от него
на расстоянии l и
движется со скоростью ux l . Для двумерных y
находится от него
на расстоянии l и
движется со скоростью ux l . Для двумерных y
![]()
равномерных потоков скорость ux зависит только от y , значит ux dux
y dy
Пусть некоторая масса жидкости перенеслась из нижнего слоя в верхний благодаря вертикальному импульсу скорости. Смешиваясь со вторым слоем, эта масса приобретает dux
![]() его
скорость. При этом в верхнем слое наблюдается пульсация скорости ux l .
его
скорость. При этом в верхнем слое наблюдается пульсация скорости ux l .
Прандтль предположил, что величины ux и uy одного порядка, тогда uy l . dy
Повторим: Прандтль предположил, что пульсации скорости в потоке по разным осям одного порядка и что величина этих пульсаций пропорциональна градиенту средней скорости.
Подставим выражения для пульсационных составляющих в формулу для касательного напряжения
2
![]()
![]() лам
турб
dudyx l2
ddyux
лам
турб
dudyx l2
ddyux
здесь l – длина пути перемешивания (см. теорию турбулентности Прандтля).
![]() dux Величина приближенно
пропорциональна средней скорости потока. При больdy
dux Величина приближенно
пропорциональна средней скорости потока. При больdy
ших скоростях, в развитом турбулентном движении, второе слагаемое существенно больше первого, и первым можно пренебречь.
Вывод: при развитом турбулентном движении касательные напряжения растут пропорционально квадрату скорости (квадратичная область сопротивления).
![]()
![]()
Когда значение лам сопоставимы со значениями турб общее касательное напряжение зависит от средней скорости в степени меньше, чем вторая.
Распределение скоростей в круглой трубе при турбулентном режиме
Структура турбулентного потока – ламинарный пограничный слой (ламинарная пленка) толщиной вп , в котором скорость нарастает по мере удаления от стенки (парабола) и ядро потока, в котором скорость распределена по логарифмическому закону.
Выведем закон распределения скорости в круглой трубе для турбулентного ядра потока. Пренебрегаем напряжением от молекулярной вязкости, тогда инерционное касатель2
ное напряжение определится по
формуле турб l 2![]() du
, где l –
длина пути переdy
du
, где l –
длина пути переdy
мешивания при переходе жидкости из оного слоя в другой.
Примем допущение: эта длина пропорциональна расстоянию от стенки (по Прандтлю) l y , где – коэффициент пропорциональности, определяемый из опыта. 2
![]() турб 2y 2
турб 2y 2![]() du
или турб
y
du
или турб
y ![]() du .
du .
dy dy
турб
![]() Введем
новый параметр движения – «динамическую скорость» u* .
По ос-
Введем
новый параметр движения – «динамическую скорость» u* .
По ос-
![]() новному уравнению
равномерного движения , справедливому и для турбулентного режима, турб RгJ gRгJ . Тогда u* g RгJ , имеет размерность
скорости.
новному уравнению
равномерного движения , справедливому и для турбулентного режима, турб RгJ gRгJ . Тогда u* g RгJ , имеет размерность
скорости.
u* y ![]() du Отсюда du
u* dy Интегрируем u
u* lny C . Следовательно dy y
du Отсюда du
u* dy Интегрируем u
u* lny C . Следовательно dy y
скорость меняется по логарифмическому закону. Постоянную интегрирования найдем из условия u uмакс при y r0 ( в центре трубы).
u* lnr0 C .
uмакс
![]() После
вычитания uмакс u 1 ln r0 . Переходим к
десятичным логарифмам и
После
вычитания uмакс u 1 ln r0 . Переходим к
десятичным логарифмам и
u* y
подставляем 0.4 (для гладких труб, для шероховатых эта величина выше 0,435)
![]() uмакс u 5.75ln r0 или u uмакс 5.75u* ln r0 . u* y y
uмакс u 5.75ln r0 или u uмакс 5.75u* ln r0 . u* y y
Для нахождения средней скорости турбулентного потока можно воспользоваться эмuмакс uср
Экспериментально установлено, что шероховатость внутренней поверхности трубы влияет на потери напора при движении жидкости. Однако это влияние проявляется не всегда.
Труба называется гидравлически гладкой, если средняя высота выступов шероховатости меньше толщины ламинарной пленки вп (вязкий подслой). В этом случае вели-
30d
чина шероховатости не влияет на потери напора. Напомним вп
Если абсолютная шероховатость больше толщины ламинарной пленки >вп , то труба называется гидравлически шероховатой. В этом случае шероховатость существенно влияет на движение жидкости.
Относительная шероховатость отнесена к диаметру трубы – относительная шерохо-
ватость
![]() .
d
.
d
Величина, обратная относительной шероховатости, называется относительной глад-
![]() 1 d костью .
1 d костью .
Потери напора по длине трубопровода определяются по формуле Дарси-Вейсбаха
2 l v h
![]() ,
где
– коэффициент гидравлического трения (коэффициент Дарси). d 2g
,
где
– коэффициент гидравлического трения (коэффициент Дарси). d 2g
Потери существенно зависят от диметра труб, вязкости жидкости, скорости ее движения и шероховатости стенок труб. Из формулы можно сделать вывод, что потери пропорциональны длине трубы, обратно пропорциональны диаметру и пропорциональны квадрату средней скорости потока. Однако такой вывод будет справедлив только при неизменном коэффициенте Дарси. Фактически коэффициент Дарси в общем случае зависит от относи-
тельной шероховатости стенок трубопровода Δэ и числа Re, т.е. Δэ , Re .
Коэффициент определяется экспериментально (считается по эмпирическим формулам). Экспериментальные данные для в широком диапазоне чисел Re были получены Никурадзе. Искусственная шероховатость была получена приклеиванием на внутреннюю поверхность трубы на лаковую основу просеянного песка определенного размера. Опыты проводились для различных жидкостей, размеров шероховатости и диаметров трубопровода. Полученные опытные данные обобщены в графике Никурадзе и позволили раскрыть механизм потерь напора по длине трубы. На графике в логарифмических осях представлены величины коэффициента гидравлического трения lg(100) от lg Re при различных
![]() значениях относительной
шероховатости
. Здесь – абсолютная величина
искусd
значениях относительной
шероховатости
. Здесь – абсолютная величина
искусd
ственной шероховатости. Логарифм используется для того, чтобы охватить возможно больший диапазон значений Re, и в то же время достаточно детально представить область малых значений числа Re (ламинарный и переходный режимы движения). Каждому фиксирован-
![]()
![]()
ному значению на графике соответствует отдельная кривая, причем чем больше , тем кривая расположена выше.
![]()
1. Ламинарный режим (на прямой I). Коэффициент Дарси не зависит от шероховатости. Выражение для может быть получено теоретически 64/Re, оно хорошо согласуется с экспериментальными данными.
2. Переходный режим (между прямыми I и II). Обычно полагают, что движение в этом режиме турбулентное (ламинарный режим здесь неустойчив) и экстраполируют на эту область зависимости турбулентного режима. В турбулентном режиме выделяют три области.
3. Область гидравлически гладких труб (на прямой II). В соответствии с рассмотренной ранее структурой турбулентного потока толщина вязкого ламинарного слоя у стенки 30d
л . Величина всех неровностей меньше толщины ламинарной пленки. Здесь ко-
эффициент Дарси не зависит от шероховатости.
4. Доквадратичная область (между прямыми II и III). Чем больше шероховатость, тем раньше происходит выход выступов шероховатости из ламинарной пристеночной пленки, а значит и выход из области гидравлически гладких труб, т.е. тем раньше начинает проявляться влияние шероховатости.
5. Квадратичная область (справа от прямой III). Коэффициент Дарси не зависит от Re («автомодельность»по Re , т.е. независимость от Re). Потери напора по длине трубы пропорциональны квадрату скорости.
График Никурадзе позволяет объяснить природу гидравлического трения, однако так как он получен для искусственной шероховатости им нельзя пользоваться при естественной шероховатости. Для реальных труб выход выступов шероховатости из ламинарной пристеночной пленки происходит не одновременно, кривые не имеют минимума.
Для естественной шероховатости вводят понятие абсолютной эквивалентной шероховатости э , т.е. такой равномерной шероховатости, для которой потери в квадратичном режиме те же, что и у естественной шероховатости.
1.3.13. Формулы для определения коэффициента гидравлического трения
64
1.
0
Re2320. Ламинарный режим. ![]() . (Единственный случай, когда формула Re
. (Единственный случай, когда формула Re
для коэффициента Дарси может быть получена теоретически. Все остальные формулы получены по экспериментальным данным – эмпирические формулы). В курсе гидропривода 75
обычно
используют формулу ![]() , в которой учтены потери на начальном участке Re
, в которой учтены потери на начальном участке Re
трубы (?).
2. 2320 Re4000. Переходный режим. Как правило расчет потерь производят по формулам для турбулентного режима (см. ниже), однако для этой области существует редко
используемая
формула Френкеля ![]() .
Re
.
Re
3.
4000
Re
20 ![]() d . Турбулентный режим.
Область гидравлически гладких труб. Форэ
d . Турбулентный режим.
Область гидравлически гладких труб. Форэ
мула
Блазиуса
![]() . Иногда встречается в виде
(100Re)0,25. Re
. Иногда встречается в виде
(100Re)0,25. Re
4. 20 ![]() d Re 500
d Re 500 ![]() d . Турбулентный режим.
Доквадратичная область.
d . Турбулентный режим.
Доквадратичная область.
э э
![]() Формула Альтшуля 0,11э
680,25.
Наиболее часто используемая формула, ре-
Формула Альтшуля 0,11э
680,25.
Наиболее часто используемая формула, ре-
комендована к применению.
d
![]() 5. 500
Re. Турбулентный
режим. Квадратичная область сопротивления.
5. 500
Re. Турбулентный
режим. Квадратичная область сопротивления.
э
0,25
Формула Шифринсона 0,11э .
d
Области 4 и 5 иногда называют областью шероховатых труб ( в отличие от области 3 – гидравлически гладких труб), причем область 5 – областью вполне шероховатых труб. Формула Альтшуля при больших числах Re дает совпадение с формулой Шифринсона (второе слагаемое в скобках становится пренебрежимо мало), а при малых – с формулой Блазиуса (первое слагаемое относительно мало).
Экспериментально получена формула Колбрука и Уайта
![]() 1
1
проверить звук 27 мин 10 ЛК
Можно предположить, что как при ламинарном, так и при турбулентном движении du
справедливы закон внутреннего трения Ньютона , а значит и опирающиеся на dy
него уравнения Навье-Стокса
![]() 1 p 2ux
2ux
2ux
dux (и т.д. по осям y и z)
1 p 2ux
2ux
2ux
dux (и т.д. по осям y и z)
X v
x x2 y2 z2 dt
Однако использовать уравнения Навье-Стокса для турбулентного режима движения практически невозможно, так как входящие в них мгновенные скорости и давления являются пульсирующими величинами. Поэтому для турбулентного режима ставится задача отыскания осредненных во времени скоростей и давлений.
Для получения уравнений Рейнольдса используются уравнения Навье-Стокса, все члены которых подвергаются операции осреднения.
Операция осреднения основана на предположении о существовании для данного турбулентного движения такого интервала осреднения Т, что выполненное по нему осреднение не изменяется при повторном осреднении.
![]() 1 T u T udt
1 T u T udt
0
Операция осреднения производится по определенным правилам.
Пусть f и p суть зависимые переменные, которые необходимо осреднить, и пусть s – есть одна из независимых переменных ( x, y,x,t ).
Правила осреднения
1. ![]() f f прим.: повторное
осреднение осредненной есть сама осредненная
f f прим.: повторное
осреднение осредненной есть сама осредненная
2. f p f p : осредненная сумма есть сумма осредненных
3. f p f p : осреднение произведения осредненной на неосредненную есть произведение осредненных
f f
4. ![]() :
осреднение производной есть производная осредненной
:
осреднение производной есть производная осредненной
s s
5. fds fds: осреднение интеграла есть интеграл осредненной
Запишем первое из уравнений Навье-Стокса (остальные преобразуются аналогично)
![]()
![]()
![]()
![]() 1 p 2 ux
ux ux
ux uy
ux uz
1 p 2 ux
ux ux
ux uy
ux uz
X v ux
x t x y z (*)
Движение установившееся, значит локальная производная скорости в правой части
![]() уравнения
равна нулю ux 0.
уравнения
равна нулю ux 0.
t Конвективную часть производной преобразуем.
Предварительное замечание. Рассмотрим сумму производных произведений скоростей и приведем ее к виду правой части имеющегося уравнения.
![]()
![]()
![]()
uxux uxuy uxuz
x y z
u
![]()
![]()
![]()
![]() x
ux ux ux ux uy
x
ux ux ux ux uy ![]() uy ux ux uz uz ux
uy ux ux uz uz ux
x x y y z z
![]()
![]()
![]()
![]()
uxx
ux uyx uy uzx uz uxuxx uyy uzz
uxx
ux uyx uy uzx uz uxuxx uyy uzz
![]() Уравнение
неразрывности в дифференциальной форме ux
uy
uz
0
Уравнение
неразрывности в дифференциальной форме ux
uy
uz
0
С учетом приведенных замечаний получим
![]()
![]()
![]()
![]() 1 p 2
uxux
uxuy
uxuz
1 p 2
uxux
uxuy
uxuz
X v ux
x x y z
Выполнив операции осреднения членов уравнения получим
![]()
![]() 1 p 2
1 p 2
X v ux uxux uxuy uxuz
x x y z (*)
Вспомним, что мгновенная скорость представляется суммой осредненной и пульса-
![]()
![]() ционной
составляющей ux
ux ux, uy
u y uy и uz
uz uz . Осредненная
пульсационная составляющая равна нулю ux
uy
uz
0
ционной
составляющей ux
ux ux, uy
u y uy и uz
uz uz . Осредненная
пульсационная составляющая равна нулю ux
uy
uz
0
При дальнейших преобразованиях учтем, что
![]() uxux
ux ux ux ux
u2x 2uxux
ux2
uxux uxux uxuy
ux uxuy uy
uxuy uxuy uyux uxuy
uxuy uxuy
uxux
ux ux ux ux
u2x 2uxux
ux2
uxux uxux uxuy
ux uxuy uy
uxuy uxuy uyux uxuy
uxuy uxuy
uxuz ux uxuz uz uxuz uxuz uzux uxuz uxuz uxuz
Произведем преобразование правой части полученного выше уравнения
uxux uxux uxuy uxuy uxuz uxuz
x x x
![]()
![]()
uxx ux
uyx uy
uzx uz uxuxx
uyy
uzz
uxxux
uxyuy
uxzuz
uxx ux
uyx uy
uzx uz uxuxx
uyy
uzz
uxxux
uxyuy
uxzuz
После осреднения уравнение неразрывности ux u y uz 0, значит скобка при
x y z
![]()
ux в правой части равна нулю.
![]()
![]()
![]() X 1 p v2u
X 1 p v2u![]()
uxux
uxuy
uxuz
ux ux
ux uy
ux uz
uxux
uxuy
uxuz
ux ux
ux uy
ux uz
x
x x y z x y z
(*)
Каждый из членов, содержащих пульсационные составляющие скорости, можно переписать в ином виде:
![]()
![]() uxux
1
uxux
uxuy
1
uxux
1
uxux
uxuy
1
uxuy
uxux
1
uxuz
x x y y z z
Уравнения Рейнольдса:
X ![]()
![]()
![]() 1 p v2ux 1 uxux
1
1 p v2ux 1 uxux
1
uxuy
1
uxuz
x x y z
ux ux ux
|
ux uy uz x y z 1 1 1 1 |
|
![]()
![]()
p 2
p 2
yux
uyuy
uyuz
Y v uy u
![]()
y x y z
y x y z
uy uy uy
ux uy uz
x y z
Z
![]()
![]() 1 p v2uz 1 uzux
1
1 p v2uz 1 uzux
1
uzuy
1
uzuz
z z y z
![]()
uz ux
uz uy uz uz
uz ux
uz uy uz uz
x y z
Члены вида uxuy имеют размерность напряжений. Таким образом в левой части
2![]() уравнений имеются члены, отражающие действие только вязкостных напряжений v ux
уравнений имеются члены, отражающие действие только вязкостных напряжений v ux
и содержащие напряжения, связанные с пульсациями скоростей, т.е. появляющиеся только
1 1
1
![]()
![]() при турбулентном режиме
движения uxux, uxuy , uxuz .
при турбулентном режиме
движения uxux, uxuy , uxuz .
x y z
При турбулентном режиме касательные напряжения могут быть представлены суммой вязкостных лам и касательных напряжений, появляющихся вследствие турбулентных пульсаций турб :
лам турб .
![]()
Турбулентные касательные напряжения выражаются формулой турб jk ujuk
, при этом они подчиняются свойству взаимности jk kj.
Полученная система является незамкнутой.
Проблема замыкания уравнений Рейнольдса в общем виде не решена.
Тема 1.4. Истечение жидкостей
p0 Рассмотрим истечение через круглое отверстие в бо-
![]() ковой стенке сосуда,
в котором поддерживается постоянный напор H 0.
ковой стенке сосуда,
в котором поддерживается постоянный напор H 0.
Тонкая стенка – толщина стенки не влияет на форму струи, струя качается только внутренней острой кромки.
Ориентировочно 0,2d .
Малое отверстие – геометрический напор в пределах отверстия можно считать постоянным (а значит и скорости в пределах сечения одинаковы). Условие – высота отверстия не превышает 0,1Н . Важен не абсолютный размер отверстия, а соизмеримость его высоты и напора. Так узкая вертикальная щель – большое отверстие, а отверстие в днище сосуда – ма-
лое (напор во всех его точках одинаков).
Кроме того, необходимо, чтобы скорость подхода жидкости к отверстию была пренебрежимо мала (площадь сечения бака много больше площади отверстия).
Если на поверхность жидкости в баке действует избыточное давление p0, то при изучении истечения следует принимать во внимание действительный напор на уровне оси от-
p0 . Предполагается, что истечение происходит в атмосферу и давлеверстия H H0
g
2 d
ние в сечении С С равно атмосферному. Площадь отверстия F ![]() . 4
. 4
Сжатое сечение струи – ближайшее к отверстию сечение струи, в котором скорости параллельны. Сжатое сечение находится на расстоянии 0,5d от внутренней поверхности стенки резервуара. На рисунке обозначено С С , площадь поперечного сечения струи в этом сечении обозначается Fс .
Коэффициент сжатия струи – отношение сжатого живого сечения к площади отвер-
стия Fс 1. F
Сжатие струи может быть полным или неполным по периметру отверстия.
Неполное сжатие – стенки или дно сосуда совпадают с краем отверстия и по части периметра сжатия нет. Коэффициент сжатия больше, расход больше. Полное сжатие может быть совершенным и несовершенным.
![]() Совершенное сжатие
– максимально возможное сжатие струи при отсутствии влияния свободной
поверхности, боковых стенок и дна сосуда.
Совершенное сжатие
– максимально возможное сжатие струи при отсутствии влияния свободной
поверхности, боковых стенок и дна сосуда.
Имеет место при расстоянии до стенок больше утроенного поперечного размера отверстия.
Несовершенное сжатие – когда стенки или дно сосуда расположены близко от отверстия. Коэффициент сжатия больше, расход больше.
Инверсия струи – изменение формы живого сечения струи в полете. Наиболее ярко это явление наблюдается при истечении через отверстие полигональной формы (треугольник, квадрат). Струя из треугольного отверстия принимает форму звезды с ребрами, перпендикулярными сторонам треугольника. При истечении через квадратное отверстие сечение струи постепенно превращается в крест с тонкими ребрами, ориентированными нормально к сторонам квадрата.
Круг практически не меняется, лишь незначительно сжимается в вертикальном направлении (эллипс).
Инверсия объясняется совместным действием сил инерции и поверхностного натяжения.
p0 p0– избыточное давление над поверхностью
![]() воды в баке.
воды в баке.
Запишем уравнение Бернулли для потока вязкой жидкости для сечений О О (на свободной поверхности) и С С (сжатого сечения) относительно плоскости сравнения А А , проходящей через центр тяжести сжатого сечения. Очевидно zс 0 . Давление в сжатом сечении равно атмосферному, значит избыточное давление pс 0 . Скорость жидко-
A сти в сечении О О полагаем пренебрежимо малой. Потери напора выразим через коэффициент сопротивления 2 hw v2сg
2 2
H0 p0 сvс vс .
g 2g 2g
Полагаем скорости одинаковыми по сжатому сечению, т.е. с 1.
Введем понятие действующего напора H H0 p0 . Это означает замену избыg
точного давления над поверхностью жидкости дополнительным столбом жидкости , производящим такое же давление. Этот прием часто используется в гидравлике для упрощения вычислений.
2 H vс 1 => vс 2g
![]()
![]() Обозначим
коэффициент скорости ,
тогда vс
2gH .
Обозначим
коэффициент скорости ,
тогда vс
2gH .
При истечении из отверстия идеальной жидкости (течение без потерь), ее скорость соответствует полному переходу потенциальной энергии в кинетическую:
![]() v ид
2gH – формула
Торричелли (1641 г.)
v ид
2gH – формула
Торричелли (1641 г.)
2 mv Действительно, умножив на массу, получим ![]()
mgH .
mgH .
2
Коэффициент скорости vс vс .
![]() 2gH v ид
2gH v ид
Физический смысл коэффициента скорости – это отношение действительной скорости истечения к теоретически возможной при отсутствии потерь энергии.
Обозначим площадь сжатого сечения Fс . Коэффициент сжатия струи , где
F
F – площадь отверстия. Очевидно Fс F . Расход жидкости через отверстие
![]() Q Fсvс F 2gH F 2gH , где
– коэффициент расхода.
Q Fсvс F 2gH F 2gH , где
– коэффициент расхода.
Q Q Q
Очевидно
F 2gH Fv ид Qид
Физический смысл коэффициента расхода – отношение действительного расхода через отверстие к теоретически возможному при отсутствии сжатия струи и потерь энергии.
В результате опытов установлено 0,600,64 0,97 0,600,62
![]() Q F 2gH
0,62 Расход через малое незатопленное от-верстие в
тонкой стенке
Q F 2gH
0,62 Расход через малое незатопленное от-верстие в
тонкой стенке
![]() Значения коэффициентов
сжатия ,
скорости ,
расхода
и сопротивления зависят в первую очередь от формы
и размеров отверстия, условий подхода к нему жидкости а также от числа
Рейнольдса, которое обычно рассчитывается по теоретической скороd 2gH
Значения коэффициентов
сжатия ,
скорости ,
расхода
и сопротивления зависят в первую очередь от формы
и размеров отверстия, условий подхода к нему жидкости а также от числа
Рейнольдса, которое обычно рассчитывается по теоретической скороd 2gH
сти Re .
С увеличением числа Re, т.е. уменьшением влияния
1,0сил вязкости, коэффициент
![]() возрастает в связи с
возрастает в связи с
0,8уменьшением ;
коэффициент уменьшается вследствие уменьше-
0,6ния торможения жидкости у кромки отверстия и увели-
0,4чения радиусов кривизны
поверхности струи на ее участке от кромки до цилин-
2 3 4 5 lgRe дрической части.
Опыты показывают, что при Re 105влияние сил вязкого трения на коэффициенты истечения практически отсутствует (квадратичная зона сопротивления) 0.62.
p1 При истечении через отверстие под уро-
![]() вень жидкости
отверстие называют затопленным. Рассмотрим истечение через затопленное
отверстие при условии, что положение свободных поверхностей жидкости по обе
стороны от отверстия не изменяется во времени, давление на свободной
поверхности до отверстия и за ним атмосферные.
вень жидкости
отверстие называют затопленным. Рассмотрим истечение через затопленное
отверстие при условии, что положение свободных поверхностей жидкости по обе
стороны от отверстия не изменяется во времени, давление на свободной
поверхности до отверстия и за ним атмосферные.
2 H1 const , H 2 const , p1 p2 pат
Действующий напор H H1 H 2
0,62 Расход через малое затопленное отверстие в тонкой стенке
Перепад давлений на отверстии p gH1 gH 2 gH1 H2
2p Расход через отверстие при известном перепаде давлений.
Дроссель – это затопленное отверстие.
pат Рассмотрим истечение жидкости из призма-
![]() тического резервуара (с постоянным поперечным сечением )
через малое отверстие в днище площадью F .
тического резервуара (с постоянным поперечным сечением )
через малое отверстие в днище площадью F .
Необходимо найти время, за которое напор изменится от H1 до H 2 .
При истечении имеет место квазиустано-
Hвившееся движение.
При расчете параметров квазиустановившеz гося потока принято время истечения разбивать на большое число малых интервалов dt и в пределах каждого интервала считать
движение установившимся.
За малое время dt можно считать напор z и расход Q постоянными.
![]() Q F 2gz .
Q F 2gz .
За рассматриваемый промежуток времени dt из бака вытечет объем dV Q dt .
В то же время при понижении уровня в баке на величину dz из него вытечет объем dV dz ( dz отрицательно, т.к. z уменьшается). Приравняем и преобразуем
![]() F 2g zdt dz => dt
dz
F 2g zdt dz => dt
dz
![]() F 2g z
F 2g z
Проинтегрируем это уравнение в пределах от H1 до H 2 (для смены знака меняем пределы интегрирования)
H2 H1 dz H1
![]() t H1dt F 2g H2 z F 2g 2 z H2
t H1dt F 2g H2 z F 2g 2 z H2
![]() t 2
H1 H2 Время
истечения из призматического сосуда площа-дью через
малое отверстие в днище площадью F
t 2
H1 H2 Время
истечения из призматического сосуда площа-дью через
малое отверстие в днище площадью F
F 2g при понижении уровня от H1 до H 2 .
Поставленная задача решена.
![]() Полагая
H 2 0 получим время полного
опорожнения сосуда t0 2 H1 .
Полагая
H 2 0 получим время полного
опорожнения сосуда t0 2 H1 .
F 2g
![]() Проанализируем полученное
выражение, для чего числитель и знаменатель умножим на H1 :
Проанализируем полученное
выражение, для чего числитель и знаменатель умножим на H1 :
2H1 . Заметим, что объем сосуда V0 H1, расход при постоянном
t0
![]() F 2g H1
F 2g H1
![]() напоре,
равном H1, был ранее получен QH1 F 2g H1 . Таким образом:
напоре,
равном H1, был ранее получен QH1 F 2g H1 . Таким образом:
![]() 2V0 . t0
2V0 . t0
QH1
Вывод: при постоянном напоре H1 заключенный в сосуде объем жидкости вытекает в 2 раза быстрее, чем при полном опорожнении того же сосуда с изменением напора от H1 до 0.
Насадок – присоединенная к отверстию короткая труба, в которой имеется напорное движение. ( в гидравлике используется термин «насадок»(муж. род), в технике термин
«насадка»(жен. род), означающий съемную часть чего-либо.) Незатопленный насадок – при истечении в газовую среду. Затопленный – при истечении под уровень.
Внешний цилиндрический насадок (насадок Вентури[10]) – прямая цилиндрическая труба длиной l (3 4)d , присоединенная под прямым углом с внешней стороны резервуара к отверстию того же диаметра.
pат При входе в такую короткую
![]() трубку происходит
сжатие потока ( по аналогии с истечением через отверстие). Площадь сжатого
сечения Fс .
трубку происходит
сжатие потока ( по аналогии с истечением через отверстие). Площадь сжатого
сечения Fс .
За сжатым сечением следует расширение потока до заполнения всего поперечного сечения насадка. Между транзитной струей и стенкой насадка образуется кольцевая вихревая водоворотная зона.
Находящаяся в ней жидкость (и воздух) уносятся транзитным (поступательно движущимся) потоком. В этой зоне понижается давление, создается вакуум.
В связи с наличием вакуума действующий напор увеличивается на значение вакуума в сжатом сечении. Скорость в сжатом сечении возрастает по сравнению с истечением через отверстие с острой кромкой. Насадок как бы «подсасывает» жидкость из бака.
В то же время в насадке происходят и дополнительные по сравнению с отверстием с острой кромкой потери напора, связанные с внезапным расширением струи за сжатым сечением. Соотношение этих факторов определяет расход через насадок.
Запишем уравнение Бернулли для потока вязкой жидкости. (Сечения 0-0 на поверхности жидкости в баке и сечение 1-1 на выходе из насадка Плоскость сравнения проходит через ось насадка. )
2 2
H ат 00 0 pат ![]() hц.н p
hц.н p
Давления равны атмосферному, сокращаются. Скоростным напором в баке пренебрегаем. Коэффициент Кориолиса полагаем =1.
2
H ![]() 2g hц.н
2g hц.н
Раскроем потери через отнесенный к скорости на выходе из насадка коэффициент сопротивления (формула Вейсбаха)
2 2
hц.н ц.н ![]()
H
H ![]() 1ц.н
1ц.н
2g 2g
В насадке сопротивление движению состоит из двух сопротивлений ц.н о.к в.р
1. сопротивления при сужении (аналогично отверстию с острой кромкой)
2. сопротивления при внезапном расширении от площади сжатого сечения Fс до площади на выходе из насадка F .
Расчет проводим при больших Re ( Re>105)
![]() Fс
0,610,64 0,63.
Fс
0,610,64 0,63.
Напомним, что коэффициент сжатия
F с
Коэффициент о.к(с), отнесенный к скорости в сжатом сечении равен 0,06. Произведем его пересчет для скорости в выходном сечении
о.к.(с)с2 hо.к о.к![]() 2
2
2 2 2 2
с F 1
о.к о.к.(с)
о.к.(с)
![]() Fс о.к.(с)
Fс о.к.(с)![]()
0,06
0,06![]() 0,163
0,15
0,163
0,15
Коэффициент потерь при внезапном расширении (отнесенный к скорости за расширением)
2 2 2
в.р
![]() FFс 1
FFс 1
![]() 1 1
1 1
![]() 0,1631
0,35
0,1631
0,35
Коэффициент сопротивления насадка ц.н о.к в.р 0,150,35 0,5
Из полученного ранее уравнения Бернулли найдем скорость 1
![]()
![]() 2gH ц.н 2gH
2gH ц.н 2gH
1ц.н
1 1
Коэффициент скорости ц.н 0,82
![]() 1ц.н 10,5
1ц.н 10,5
Напомним, что коэффициент скорости есть отношение действительной скорости к теоретической, вычисленной по формуле Торричелли, он меньше единицы.
Коэффициент расхода ц.н ц.н ц.н, т.к. сжатия потока нет,1.
Опыты показали, что наибольшее значение коэффициента расхода при длине насадка l 34d , когда потерями по длине можно пренебречь. При увеличении длины это уже короткая труба, потери по длине надо учитывать. Расход через внешний цилиндрический насадок
![]() Q ц.нF 2gH , где коэффициент расхода ц.н 0,82.
Q ц.нF 2gH , где коэффициент расхода ц.н 0,82.
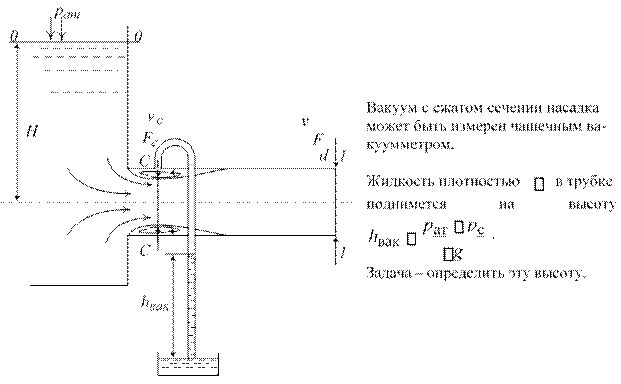
Запишем уравнение Бернулли для потока вязкой жидкости.
(Сечения 0-0 и С-С. Плоскость сравнения проходит через ось насадка.)
2 2 2
H pат 00 0 pс сс hо.к, о.к.с hо.к, о.к. 0,06
2
pат pс с с о.к H
Выразим скорость в сжатом сечении через скорость на выходе, учитывая коэффициент сжа-
тия с ![]() .
.
2
![]()
![]() 2gH , получим
ц.н2 H
2gH , получим
ц.н2 H
Используем ц.н
Получим
![]()
![]() 2 ц.н2
с
о.к
1H 0.822(10,06) 1H pат
pс 2g с
2
о.к
H 2
0.642
2 ц.н2
с
о.к
1H 0.822(10,06) 1H pат
pс 2g с
2
о.к
H 2
0.642
g 0.75H
pат pс
Вакуум в цилиндрическом насадке hвак 0,75Н
Предельное значение вакуума ограничено возможным наименьшим давлением в сжатом сечении, которое из условий отсутствия разрыва сплошности жидкости не должно быть меньше давления насыщенных паров жидкости при температуре истечения. Для воды при 20С это давление 2,34 кПа. Давление насыщения сильно зависит от температуры и, например, при 60С 20 кПа.
hвак.макс pат pнп 9,7 м вод. ст., максимальный напор Hмакс 13м g
При напорах, близких к максимальному возможно появление кавитации и нарушение сплошности потока. Жидкость отрывается от стенок, воздух поступает в насадок, истечение превращается в истечение из отверстия с острой кромкой с соответствующим уменьшением коэффициента расхода. Явление называется срыв вакуума.
Срыв вакуума при истечении из насадка – резкое уменьшение коэффициента расхода, связанное с отрывом жидкости от стенок насадка.
Для устойчивой работы практически принимают максимальный вакуум 8 м вод.ст, максимально допустимый напор 10,7 м.
При истечении через затопленный цилиндрический насадок (под уровень) коэффициент расхода при повышении напора меняется мало, отрыва потока не происходит, однако при напорах больше критического наблюдается нарушение сплошности потока, образование паровых пузырьков с последующим их захлопыванием в зоне повышенного давления. Такое явление называется кавитация.
Линии тока при входе во внутренний насадок более искривлены, площадь сжатого сечения меньше, коэффициент сжатия меньше, коэффициент расхода меньше.
Коэффициенты зависят от толщины стенок трубы.
Если насадок работает как отверстие с острой кромкой (при малой длине l 3d )
0,51 0,97 0,53 0,06
Работающий полным сечением (заполненный, при l 3d ) внутренний насадок: 0,71, 1.
![]() Усеченный конус с
углом при вершине
Усеченный конус с
углом при вершине
Коэффициент расхода определяется для выходного сечения (по выходной пощади)
![]() Q Fвых 2gH
Q Fвых 2gH
Естественно, коэффициент расхода зависит от угла при вершине ()
Максимальный коэффициент расхода макс 0,946 при 13,4о (1324') В этом насадке (единственном) коэффициент сжатия струи не равен 1.
0,98 0,965
![]()
Имеет сложную форму. Вход по форме вытекающей через отверстие струи, а затем – цилиндр.
Сжатие на выходе отсутствует 1. Коэффициенты 0,97 .
![]() Усеченный конус с
углом при вершине
Усеченный конус с
углом при вершине
Вакуум в сжатом сечении такого насадка больше, предельный напор меньше.
Обычно принимают 57o.
Сжатия в выходном сечении нет, 1.
![]() Коэффициент
расхода (по выходной площади) Q Fвых 2gH
0,45.
Коэффициент
расхода (по выходной площади) Q Fвых 2gH
0,45.
![]()
![]() Ранее получено Q F 2gH и
2gH
Ранее получено Q F 2gH и
2gH
Оценим кинетическую энергию проходящего в единицу времени
2 2
![]()
![]() m
Q
g2FH 2gH
m
Q
g2FH 2gH
2 2
Получили: при равных площади и напоре расход зависит от , а кинетическая энергия от
![]() 2 1 1
2 1 1
. Данные по коэффициентам истечения сведем в таблицу.
2
Коэффициенты истечения при больших числах Re
|
|
Наименование |
|
|
|
2 |
|
|
1 |
Отверстие в тонкой стенке |
0,64 |
0,97 |
0,62 |
0,583 |
0,06 |
|
2 |
Внешний цилиндрический насадок |
1 |
0,82 |
0,82 |
0,551 |
0,49 |
|
3 |
Внутренний цилиндрический насадок |
1 |
0,71 |
0,71 |
0,356 |
0,98 |
|
4 |
Конический сходящийся насадок ( =13) |
0,98 |
0,97 |
0,95 |
0,894 |
0,06 |
|
5 |
Коноидальный насадок |
1 |
0,97 |
0,97 |
0,913 |
0,06 |
|
6 |
Конический расходящийся насадок ( =5…7, данные отнесены к выходному сечению ) |
1 |
0,45 |
0,45 |
0,091 |
3,94 |
![]() Формулу
для расхода Q Fвых 2gH и коэффициенты в
рамке знать наизусть.
Формулу
для расхода Q Fвых 2gH и коэффициенты в
рамке знать наизусть.
Выводы по таблице. Наибольшая скорость истечения 1,4,5
Максимальный расход 4,5 Максимальная кинетическая энергия струи 5
Минимальная скорость и кинетическая энергия 6.
Жиклёр (франц. gicleur, от gicler – брызнуть), калиброванное отверстие для дозированной подачи жидкого топлива или воздуха. В технической литературе жиклерами называют детали карбюратора (пробки, форсунки) с калиброванными отверстиями.
По выполняемым функциям и в зависимости от того, в какой системе карбюратора он установлен, различают жиклеры топливный, воздушный, главный, компенсационный, холостого хода и др.
Жиклёр оценивают их пропускной способностью (производительностью), т.е. количеством жидкости (обычно воды), которое может пройти через калиброванное отверстие в единицу времени; пропускная способность Ж. выражается в см3/мин.
Гидравлический дроссель – устройство, устанавливаемое на пути движения жидкости для ограничения её расхода или изменения давления в канале. Гидравлические дроссели бывают постоянными (нерегулируемыми) и переменными (регулируемыми). К постоянным Г. д. относятся капилляры, втулки, шайбы, пакеты шайб; к переменным - золотниковые пары, дроссели типа сопло – заслонка, винтовые дроссели. В зависимости от режима потока жидкости в рабочем канале (ламинарного или турбулентного) Гидравлические дроссели могут быть линейными, на которых перепад давлений пропорционален расходу жидкости, и квадратичными, на которых перепад давлений пропорционален квадрату расхода протекающей жидкости. Гидравлические дроссели применяют для изменения расхода рабочей жидкости с целью регулирования скорости рабочих органов машин; создания требуемых перепадов давления рабочей жидкости в гидросистемах; управления гидроусилителями в следящих гидроприводах.
Потоки жидкости или газа, не имеющие твердых границ, называются ждкими или газовыми струями.
Классификация: затопленные (вода в воде), незатопленные (вода в воздухе); свободные и ограниченные (пристеночные); по форме осесимметричные (круглое сечение) и плоские.
В структуре незатопленной струи 3 части.
1) компактная часть (сплошной цилиндр)
2) раздробленная часть (крупные части)
3) распыленная часть (отдельные капли)
Силы, действующие на струю: тяжести, сопротивления среды, инерционные силы от вихрей турбулентности, поверхностного натяжения.
![]() Из сопла площадью сечения F0 со скоростью v 0 вылетает струя жидкости и ударяется о криволинейную преграду.
Из сопла площадью сечения F0 со скоростью v 0 вылетает струя жидкости и ударяется о криволинейную преграду.
Струя разбивается на две части, обреx кает преграду и со скоростью v под углом к горизонту покидает преграду. r Сила действия струи на преграду Pr,
сила воздействия преграды на струю R
. r r
Очевидно R P .
Применим к жидкости, заключенной между сечениями 0-0 и 1-1 (1’-1’) теорему об изменении количества движения в проекции на ось x . Изменение количества движения равно импульсу силы. m
2 ![]() vcosmv0
Rt , где t – промежуток времени, m – масса жидкости, 2
vcosmv0
Rt , где t – промежуток времени, m – масса жидкости, 2
проходящая через сечение за это время. Трением и весом пренебрегаем, тогда по закону
m
сохранения энергии v v0 . Учитываем, что массовый
расход Q ![]() и
и
t
PR. Получим
P Qv01 cos Сила воздействия струи на преграду
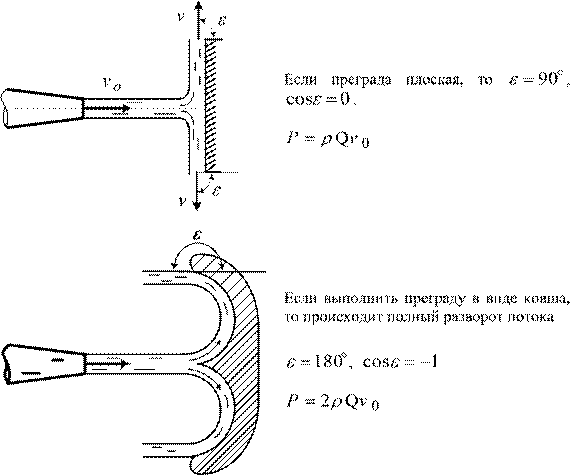
![]() Рассмотрим воздействие струи на систему плоских пластинок
(турбинное колесо)
Рассмотрим воздействие струи на систему плоских пластинок
(турбинное колесо)
Сила такого воздействия P .
Скорость схода жидкости с пла-
стинки
v (абсолютная скорость), может быть представлена как сумма скорости самой пластинки u (переносная скорость) и скорости движения жидкости по пластинке w (относительная скорость), т. е.
2 2
![]() v u w
v u w
По условию сохранения кинетической энергии струи w v0 u , это скорость, с которой струя ударяется в пластинку.
Сила воздействия струи на пластинку P Qw Q v0 u.
Мощность, которая передается пластинчатому колесу, N Pu Qu v0 u.
При постоянной плотности , расходе Q и скорости струи на выходе из сопла v 0 мощность зависит только от скорости движения пластинки u , т.е. N f (u), причем зависимость квадратичная (парабола). Ее корни:
При u 0 имеем P Pмакс, однако N 0/
При u v 0 сила воздействия P 0, и, следовательно, N 0.
Для нахождения значения u при котором величина P максимальна можно воспользоваться тем, что в точке максимума первая производная функции равна нулю. Раскроем
2 скобки N Qv 0u Qu
dN![]() 0. dN
0. dN![]() Qv 0
2Qu Q v 2u
0, откуда u v 0 . du du 0 max 2
Qv 0
2Qu Q v 2u
0, откуда u v 0 . du du 0 max 2
Тот же вывод может быть получен без взятия производной, если вспомнить, что парабола имеет максимум посередине между корнями. 2 v0 ( теоретически, в действительности Максимальная мощность N max Q 4 меньше из-за потерь, 0,92 0,96).
2 2
![]() Кинетическая
энергия струи на выходе из сопла Эк
m2v0
Qv20
Кинетическая
энергия струи на выходе из сопла Эк
m2v0
Qv20
Следовательно в случае плоской пластинки используется только половина располагаемой энергии струи, оставшаяся половина покидает лопатки со выходной скоростью w . Чтобы практически полностью использовать энергия струи следует выполнить лопатки в форме ковша с полным разворотом потока.
![]() Рассмотрим истечение струи
из резервуара через отверстие. Скорость струи (без учета потерь) определяется
по формуле Торричелли v 0 2gH , где H – действующий напор.
Если на пути струи расположить плоскую преграду, то на нее будет действовать
сила
Рассмотрим истечение струи
из резервуара через отверстие. Скорость струи (без учета потерь) определяется
по формуле Торричелли v 0 2gH , где H – действующий напор.
Если на пути струи расположить плоскую преграду, то на нее будет действовать
сила
![]() P1 Qv 0, где Q Fv F 2gH . Окончательно P1 2gHF . К слову заметим,
P1 Qv 0, где Q Fv F 2gH . Окончательно P1 2gHF . К слову заметим,
что в этом случае на резервуар действует рвная по величине и противоположная по направлению сила.
Если отверстие перекрыть неподвижной преградой, то на нее будет действовать сила гидростатического давления, равная произведению давления жидкости в резервуаре на глубине p gH на площадь P2 gHF . Интересно, что величина этой силы в два раза меньше, чем сила действия струи.
Обычно гидравлические исследования явлений, происходящих в натурных условиях (в натуре), проводят в лабораториях на моделях, воспроизводя их в том или ином масштабе.
В результате исследований на моделях получают поправочные коэффициенты к теоретическим формулам или эмпирические формулы, отражающие зависимости между отдельными параметрами, которые характеризуют изучаемое явление. Различают физическое, аналоговое и численное моделирование.
Гидравлическое моделирование – исследуется не сам поток, сооружение или машина, а их модели, выполненные обычно в уменьшенном масштабе.
Моделирование различают: физическое, аналоговое, численное
1. Физическое – модель имеет ту же физическую природу
При физическом моделировании на модели исследуют явление, имеющее ту же физическую природу, что и в натуре (например, истечение воды через водослив в натуре и на модели).
2. Аналоговое – природа разная, но описывается теми же уравнениями (аналоговая вычислительная машина = АВМ)
При аналоговом моделировании явления в натуре и на модели имеют разную физическую природу, однако описываются аналогичными системами математических уравнений (например напорное движение грунтовых вод и распределение электрического потенциала в проводнике). Ранее для моделирования физических процессов широко использовались аналоговые вычислительные машины (АВМ), представляющие собой набор электрических элементов, соединяемых в электрические цепи.
3. Численное моделирование – решение задач на ЭВМ (математическая модель)
Численное моделирование представляет собой решение гидравлических задач с помощью численных методов на ЭВМ без выполнения лабораторных исследований.
Общие условия механического подобия:
Явления будут механически подобны если в них одинаково отношение всех геометрических элементов (размеров, расстояний, перемещений), одинаково отношение плотностей, кинематических параметров (скоростей, ускорений) и сил, действующих в соответствующих точках и направлениях.
Для полного механического подобия явлений (потоков) необходимо их геометрическое, кинематическое и динамическое подобие.
Виды подобия:
1. Геометрическое
подобие: между соответствующими линейными размерами существует постоянное соотношение
lн ![]() lм
Ml .
lм
Ml .
![]() 2 Тогда
соотношение площадей можно записать так: FнFм MF Ml
2 Тогда
соотношение площадей можно записать так: FнFм MF Ml
![]() 3.
3.
Отношение объемов VнVм MV Ml
В геометрически подобной модели русла все
размеры, в том числе и высота выступов
шероховатости, должна быть меньше, чем в натуре в Ml раз и,
следовательно, в подобных потоках относительная шероховатость такая же, как и в
натуре ![]() R idem . 2. При кинематическом
подобии подобны поля скоростей и ускорений.
R idem . 2. При кинематическом
подобии подобны поля скоростей и ускорений.
Если некоторая жидкая частица в натуре за интервал времени Tн проходит участок траектории lн, то для подобия необходимо, чтобы соответствующая жидкая частица на модели за некоторое (другое) время Tм прошла отрезок траектории lм .
При этом отношение между интервалами времени Tн ![]() Tм
Mt .
Tм
Mt .
![]() Для
скоростей сходственных точек н м
M,
для ускорений aн
Для
скоростей сходственных точек н м
M,
для ускорений aн![]() aм Ma .
aм Ma .
Скорости и ускорения должны быть представлены одинаково ориентированными в пространстве векторами.
Отметим, что с учетом геометрического подобия:
![]()
![]() Ml , Ma M
M2l
Ml , Ma M
M2l
M
Mt Mt Mt
3. Для динамического
подобия необходимо, чтобы силы, действующие на любую пару сходственных
элементов были подобны: Pн ![]() Pм
MР .
Pм
MР .
Потоки жидкости, удовлетворяющие одновременно условиям геометрического, кинематического и динамического подобия, называют гидродинамически подобными, а коэффициенты пропорциональности M – масштабными множителями.
Выбор всех масштабных множителей для подобных потоков не является произвольным. Между ними имеется определенная связь.
Равнодействующую сил, действующих на произвольно взятую жидкую частицу, можно выразить через произведение массы на ускорение, причем массу представим как произведение плотности на объем. В масштабных множителях имеем MР MMl3Ma. Масштабный множитель ускорения можно выразить через масштабные множители длины 4
![]() и
времени Ma
M2l
, тогда MР
MM2 l .
и
времени Ma
M2l
, тогда MР
MM2 l .
Mt Mt
2 2 2 2 2. (не стирать, потребу-
![]() Заметим,
что Ml Mt
M,
тогда MР
MMl M
Заметим,
что Ml Mt
M,
тогда MР
MMl M
ется ) (*)
![]() 1MР2 2 1 закон подобия
Ньютона в масштабных множите-
1MР2 2 1 закон подобия
Ньютона в масштабных множите-
MMl M лях
Заменим масштабные множители соответствующими отношениями:
![]() P2н 2 P2м 2 или Neн
Neм, где Ne
P2н 2 P2м 2 или Neн
Neм, где Ne ![]() lP22 критерий Ньютона.
lP22 критерий Ньютона.
нlнн мlмм
Гидродинамическое подобие явлений требует равенства критериев Ньютона, соответствующих модели и натуре.
На частицу жидкости в общем случае действуют силы тяжести, трения, давления.
1. Сила тяжести => число Фруда
Сила тяжести пропорциональна массе и ускорению свободного падения. Масса есть произведение плотности на объем (куб линейного размера частицы) 3 3
G mg gV gl в масштабных множителях MG MMgMl
Учитывая (*) и полагая, что сила тяжести является преобладающей силой, имеем
2
![]() MMl2M2
M 3
откуда M
1
MMl2M2
M 3
откуда M
1
MgMl M gMl
заменяем масштабные множители соответствующими отношениями и вводим число Фруда
2
сила инерции
Геометрически подобные потоки, в которых преобладает действие сил тяжести, можно считать динамически подобными если будут равны числа Фруда для сходственных сечений обоих потоков.
Записывается : Frн Frм или Fr idem.
Если положить, что Mg 1, то
M Ml0.5 или н мMl0.5 (если Ml 100, то н 10м )
MQ MFM Ml2Ml0.5 Ml2.5 (если Ml 100, то Qн 105Qм)
2. Сила трения => число Рейнольдса
Закон вязкого трения Ньютона для касательного напряжения dy
Сила трения есть произведение касательного напряжения на площадь. d
T F l в масштабных множителях MT MMMl dy
![]() Учитывая (*) и полагая, что
силы инерции являются преобладающими силами, имеем MMl2M2
MMMl откуда (учитывая,
что v ) MMlMv
1.
Учитывая (*) и полагая, что
силы инерции являются преобладающими силами, имеем MMl2M2
MMMl откуда (учитывая,
что v ) MMlMv
1.
Число Рейнольдса Re ![]() Re
Re ![]()
3. Сила давления => число Эйлера
Сила давления пропорциональна гидродинамическому давлению p и площади F
2 2
P pF pl в масштабных множителях MP M pMl
Учитывая (*) и полагая, что силы давления являются преобладающими силами, имеем
MMl2M2
M pMl2 , откуда ![]() M p 2 1
M p 2 1
MM
Критерий Эйлера Eu ![]() Eu
Eu ![]()
Кроме перечисленных есть еще много других критериев подобия Перечислим некоторые из них:
Критерий Вебера (силы поверхностного натяжения)
Критерий Архимеда (подъемная сила – сила Архимеда)
Критерий Маха (число Маха) (влияние сжимаемости при обтекании тела потоком, отношение скорости тела (потока) к скорости звука. М=1 – граница, больше – сверхзвуковой поток)
Критерий Коши (действие упругих сил – гидравлический удар в трубах)
Критерий Струхаля – (неустановившееся движение)
Критерий Лагранжа – (медленное течение вязких жидкостей)
Число Прандтля – теплопроводность
В реальности не удается обеспечить учет более чем одного критерия подобия.
Рассмотрим, например, одновременное выполнение критериев Фруда и Рейнольдса.
2 2
![]() Критерий Фруда Fr v
Критерий Фруда Fr v![]() . В масштабных множителях Mv 1. gl M g M l
. В масштабных множителях Mv 1. gl M g M l
![]() Предположим,
что Mg 1. Тогда для подобия
необходимоMv M l .
Предположим,
что Mg 1. Тогда для подобия
необходимоMv M l .
![]() l v M
l Mv 1. С уче-
l v M
l Mv 1. С уче-
Критерий Рейнольдса Re . В масштабных множителях
M
том полученного из критерия Фруда соотношения получим M M l1.5.
Если предположить, что M l 10 , то необходимо обеспечить по вязкости
M 101.5 31.6. Выполнить это условие практически невозможно. Разумеется, можно попытаться поменять M g ( ранее мы предположили, что Mg 1), однако успех еще более
проблематичен.
При моделировании в первую очередь важно решить какие силы являются доминирующими в моделируемом явлении, тем самым выбрать определяющий критерий подобия.
Безнапорные потоки – сила тяжести – критерий Фруда Напорные потоки – сила трения – критерий Рейнольдса.
При турбулентном движении в квадратичной области сопротивления характер течения не зависит от числа Re (это явление называется «автомодельность»).
В этом случае условия подобия определяются при Eu=idem и =idem (неизменность коэффициента Шези).
С помощью теории моделирования удается создать лабораторную модель так, что процессы, происходящие в ней подобны процессам, происходящим в натуре. Зная масштабные множители можно перевезти значения параметров, измеренные на модели, в натуральный масштаб.
Модель судна в бассейне, модель гидроэлектростанции в лаборатории.
Тема 1.5. Трубопроводы
Различные способы расчета потерь. Рассматривается равномерное напорное движение жидкости в круглой трубе. При равномерном движении форма и площадь живого сечения, средняя скорость потока и эпюра скоростей по длине не изменяются. В этих условиях живое сечение характеризуется одним линейным размером – диаметром. Напомним: d 4Rг.
2 l
Общая формула для потерь напора по
длине имеет вид hl ![]() .
.
2
l
Для круглых труб hl ![]() .
.
d 2g
Это установленная экспериментально формула Дарси-Вейсбаха. Безразмерный коэффициент называют коэффициентом гидравлического трения или коэффициентом Дарси. Коэффициент гидравлического трения зависит от относительной шероховатости
![]() э ,Re
. Для нахождения существуют
эмпиричетрубопровода и числа Re.
э ,Re
. Для нахождения существуют
эмпиричетрубопровода и числа Re.
d
ские формулы (режимы ламинарный – переходный –турбулентный; область гидравлически гладких труб, доквадратичная область, квадратичная область).
![]()
![]() При равномерном движении
жидкости средняя скорость потока, не изменяющаяся l 2 8g Rгhl 8g C .
При равномерном движении
жидкости средняя скорость потока, не изменяющаяся l 2 8g Rгhl 8g C .
по длине из формулы hl ![]() равна .
Обозначим
равна .
Обозначим
4Rг 2g l
Коэффициент C называют коэффициентом Шези. Вспомним, что гидравлический
8g
![]()
![]()
C RгJ , где С .
C RгJ , где С .
2
Потери напора по длине с учетом
коэффициента Шези hl
![]() 2 .
2 .
Коэффициент Шези в отличие от безразмерного коэффициента Дарси имеет размерность С L0.5T1. В справочниках приводятся таблицы значений коэффициента
Шези для трубопроводов различного диаметра и различной шероховатости. Существует много эмпирических формул для расчета коэффициента Шези.
![]() Зная формулу для средней
скорости потока получим формулу Шези для расхода при равномерном движении Q F
FC RгJ .
Зная формулу для средней
скорости потока получим формулу Шези для расхода при равномерном движении Q F
FC RгJ .
При расчете трубопровода обычно составляют уравнение Бернулли для потока вязкой жидкости. Пренебрегая местными потерями и скоростными напорами, получаем H hl .
h
![]() Вспомним,
что гидравлический уклон J
l ,
откуда J
Вспомним,
что гидравлический уклон J
l ,
откуда J
![]() H . Подставим найден-
H . Подставим найден-
![]() ное
значение гидравлического уклона в формулу Шези для скорости потока
C RгJ
ное
значение гидравлического уклона в формулу Шези для скорости потока
C RгJ
![]() 2
2
C .
Решаем уравнение относительно напора H ![]() .
Заметим на бу-
.
Заметим на бу-
2
C Rг
дущее, что напор пропорционален квадрату скорости.
Запишем формулу Шези для расхода при равномерном движении Q FC RгJ .
![]() Объединим параметры,
зависящие от диаметра трубопровода, представим их виде так называемой расходной
характеристики трубопровода (модуля расхода) K FC Rг .
Объединим параметры,
зависящие от диаметра трубопровода, представим их виде так называемой расходной
характеристики трубопровода (модуля расхода) K FC Rг .
Расходная характеристика K представляет собой расход в данной трубе при гидравлическом уклоне, равном единице.
2
Q
![]() Тогда
расход Q
K J ,
напор H
Тогда
расход Q
K J ,
напор H ![]() l .
l .
2
K
При этом расход Q и расходная характеристика K должны быть выражены в одних и тех же единицах. В таблицах для гидравлических расчетов приводятся значения расходной характеристики K для трубопроводов различного диаметра с различной относительной шероховатостью. На этой основе производится расчет трубопроводов «с использованием таблиц».
Получим значение K расчетным путем. Гидравлический уклон равен 1, значит по-
![]() тери равны
длине h l . Потери по длине h
тери равны
длине h l . Потери по длине h ![]() . Отсюда v .
. Отсюда v .
![]() d 2 d 5g
d 2 d 5g
K Q vF; F ![]() ; K .
; K .
4 8
0.25
![]() В
квадратичной области турбулентного режима 0.11э
В
квадратичной области турбулентного режима 0.11э
d
Замечание. При равномерном движении гидравлический и пьезометрический уклоны равны. Пренебрегая скоростным напором, получим, что линия полного напора и пьезометрическая лини совпадают.
Простой трубопровод – трубопровод, не имеющий ответвлений и состоящий из труб одинакового диаметра, выполненных из одного материала.
Приведем два примера простых трубопроводов.
![]()
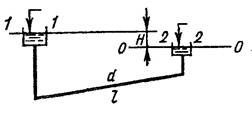
Движение жидкости в трубе обусловлено напором H , равным разности напоров в резурвуаре-питателе и приемнике или разности напоров в резервуаре питателе и в струе на выходе из трубы, если резервуар-приемник отсутствует. Если указанная разность напоров не изменяется во времени, то движение установившееся. Мы рассматриваем расчет только трубопроводов с установившимся движением.
Потери напора в трубопроводе можно рассматривать как сумму потерь на трение по длине трубопровода и потерь в местных сопротивлениях h hl hм .
По соотношению потерь по длине и в местных сопротивлениях в общей величине потерь трубопроводы делятся на гидравлически короткие и гидравлически длинные.
В гидравлически длинном (или просто длинном) трубопроводе потери напора по длине настолько превышают местные потери (и скоростной напор), что местные потери не вычисляют, а принимают как некоторую часть потерь по длине.
Практически при расчете длинных трубопроводов находят потери напора по длине hl
, а затем суммарные местные потери напора учитывают, увеличивая найденное значение hl на 510%. h 1.05 1.1hl .
В гидравлически коротком трубопроводе потери напора по длине и местные потери сопоставимы по значению. При гидравлическом расчете коротких трубопроводов учитывают как местные потери напора, так и потери по длине, а в балансе напоров учитывают скоростные напоры в сечениях потока.
При расчете простого трубопровода необходимо установить связь следующих характеристик
– диаметр трубопровода, d ;
– располагаемый напор, H ; – объемный расход жидкости, Q ;
– средняя скорость жидкости, .
Задачи по расчету трубопроводов подразделяются на задачи проектирования и задачи эксплуатации. Полагается, что длина трубопровода во всех случаях известна.
Задачи проектирования: определение диаметра трубопровода, напора или давления на одном из его концов при заданной скорости жидкости в трубе или ее расходе.
Задачи эксплуатации: определение эксплуатационных характеристик (расход, скорость жидкости) готового (существующего в натуре или в проекте) трубопровода с известным диаметром и шероховатостью, а также с определенными напорами (давлениями) на концах трубы.
По методу расчета подразделяют задачи прямые и обратные.
При решении прямых задач искомые величины находятся по расчетным формулам в явном виде. В обратных задачах искомую величину в явном виде выразить не удается, решение находят с помощью итерационных процедур.
Располагаемый напор равен потерям. Потери складываются из потерь по длине и потерь в местных сопротивлениях. Потери по длине определяются по формуле Дарси-Вейсбаха (первая водопроводная формула). Потери в местных сопротивлениях суммируются по всем местным сопротивлениям и зависят от коэффициента потерь в каждом из них i . Получаем формулу, которая связывает среднюю скорость и располагаемый напор.
H h ; h hl
2 2 l
hм; hl
![]() 2 ; hм i
2 ; hм i ![]() 2g ; d g i
2g ; d g i
![]() H h
l 2
H h
l 2
d i i 2g
2
Q
![]() При расчете трубопровода «с
использованием таблиц» H l , где расходная ха-
При расчете трубопровода «с
использованием таблиц» H l , где расходная ха-
2
K
рактеристика K берется из таблиц.
2
![]()
![]() По
определению средняя скорость потока
. Очевидно Q F
По
определению средняя скорость потока
. Очевидно Q F
![]()
![]() Число Рейнольдса Re
или Re .
Значения динамической вязкости и
Число Рейнольдса Re
или Re .
Значения динамической вязкости и
плотности или кинематической вязкости жидкости при данной температуре известны.
Коэффициент сопротивления трения ( коэффициент Дарси ) определяется по эмпирическим формулам и зависит от Re и абсолютной эквивалентной шероховатости э, которая для данного вида труб (материала, исполнения) известна (задается в справочниках, для новых стальных труб э =0,2 мм, для старых водопроводных э =1,5 мм).
Применение тех или иных эмпирических формул определяется режимом движения жидкости (числом Re ), а при турбулентном режиме областью сопротивления. I – ламинарный режим движения
![]() Границы Rе Reкр
2320 Формула
Re
Границы Rе Reкр
2320 Формула
Re
II – переходный режим движения
2,7
![]() Границы 2320 Re 4000 Формула
Границы 2320 Re 4000 Формула
Rе0,53
III – область гладких труб
![]()
![]() Границы:4000 Rе 20 d . Формула Блазиуса
0,3164
Границы:4000 Rе 20 d . Формула Блазиуса
0,3164
э Rе0,25
IV – область доквадратичного сопротивления (или переходная)
![]()
![]()
![]() Границы
: 20 d
Re
500 d .
Формула Альтшуля 0,11э
680,25
Границы
: 20 d
Re
500 d .
Формула Альтшуля 0,11э
680,25
э э d Rе
V- область квадратичного сопротивления (или шероховатых труб)
0,25
![]() Границы: 500 d Re. Формула Шифринсона 0,11э
Границы: 500 d Re. Формула Шифринсона 0,11э
э d
Задачи, чаще всего встречающиеся в практике, приведены ниже
(четыре параметра, два заданы, два оставшиеся определяются расчетом; число различных сочетаний из 4 по 2 равно 6)
|
Известны (заданы) |
Требуется лить |
опреде- |
Вид задачи |
Характеристика |
|
d и |
H и Q |
|
прямая |
проектная |
|
d и Q |
H и |
|
прямая |
проектная |
|
Q и |
H и d |
|
прямая |
проектная |
|
H и d |
Q и |
|
обратная |
эксплуатационная |
|
H и Q |
d и |
|
обратная |
проектная |
|
H и |
d и Q |
|
обратная |
учебная |
Решение прямых задач начинается с нахождения числа Re.
Задача 1. d и => Re
Задача 2. d и Q => => Re
Задача 3. Q и => d => Re
Дальнейший алгоритм расчета одинаков Re => => H .
При решении обратных задач «без использования таблиц» не удается получить аналитического решения. Следует применить итерационную процедуру, т.е. задаться искомым значением, а затем уточнять его.
Выражение для располагаемого напора следует решить относительно скорости
Задача 4 (подбираем скорость) :
H , d => задаемся => Re => => H (больше/меньше заданного) =>новое .
Задача 5 (подбираем диаметр):
H , Q => задаемся d => => Re => => Hd (больше/меньше заданного) => новое d .
Задача 6 (подбираем диаметр):
H , => задаемся d => Re => => Hd (больше/меньше заданного) => новое d .
В учебных целях рекомендуется сопровождать решение графической иллюстрацией процесса последовательных приближений. Для этого по имеющимся расчетным данным следует изобразить следующие зависимости:
Задача 4. H f (). Задачи 5 и 6. H f (d)
Графоаналитический метод решения задач обратного типа состоит в следующем ( на примере задачи 4). Задаемся значением скорости , находим напор H , который, разумеется, отличается от заданного в условии. Если полученное значение меньше заданного, то увеличиваем скорость, если больше, то уменьшаем. Повторяем расчет. Строим в масштабе зависимость H f (). Для построения зависимости необходимо не менее 3-х точек. Из полученной графической зависимости находим значение , которому соответствует заданный напор H . Производим проверку найденного значения.
Рассмотрим систему из последовательно соединенных длинных труб различных диаметров и длин. В общем случае материал труб может быть различным (различная шероховатость).
![]() Заданы расход Q , диаметры труб и длины участков. Расходные характеристики
труб
Заданы расход Q , диаметры труб и длины участков. Расходные характеристики
труб
Ki известны. По трубопроводу, составленному из последовательно соединенных труб проходит не изменяющийся по длине транзитный расход Q . На каждом i-м участке рассматриваемого трубопровода для пропуска расхода Q затрачивается часть сум марного напора Н , равная
2
Q
Hi ![]() 2
li
hli , где i =
1, 2 … n – номер участка.
2
li
hli , где i =
1, 2 … n – номер участка.
K
Поскольку местными потерями пренебрегаем, напор Н затрачивается на преодоление потерь напора по длине и будет равен сумме потерь напора на отдельных участках
![]() H Hi Q2 li2 i i Ki
H Hi Q2 li2 i i Ki
Вывод.
Для последовательного соединения расход одинаков, а напор равен сумме напоров.
Аналогия – последовательное соединение сопротивлений, ток одинаков а напряжения суммируются.
Рассмотрим систему из параллельно соединенных длинных труб.
![]() Между точками M
и N проходит несколько труб.
Между точками M
и N проходит несколько труб.
Заданы общий расход Q , длины, диаметры, материал (шероховатость) и расходные характеристики труб.
Разность пьезометрических напоров в начале и в конце труб составляет напор H , полностью затрачиваемый на преодоление со противлений. На каждом участке трубы движение происходит под действием одного и того же напора. Но так как длины участков различны, гидравлические уклоны на каждом участке будут различны.
![]() H
H
Расход, проходящий по любому участку Qi Ki. Для всех участков имеем n
уравнений для Qi . Сумма расходов на отдельных участках должна быть равна общему расходу, поступающему в систему параллельно соединенных трубопроводов в точке M и выходящему из системы в точке N.
![]() Q Qi
H Ki
Q Qi
H Ki ![]()
i i
Таким образом, имеем n+1 уравнение, из которых может быть найден необходимый напор и расход в каждом из параллельных участков. Распределение расходов между участками заранее не известно. Поэтому все расходы выражают через какой-нибудь один, напри-
Q
![]()
![]() мер через Q1. Имеем i Ki l1 , откуда Qi Q1 Ki l1 .
мер через Q1. Имеем i Ki l1 , откуда Qi Q1 Ki l1 .
Q1 K1 li K1 li
n
![]() Суммарный
расход Q
Q11i2KK1i ll1i .
Отсюда находим Q1и все остальные.
Суммарный
расход Q
Q11i2KK1i ll1i .
Отсюда находим Q1и все остальные.
Вывод.
Для параллельного соединения напор одинаков, а расход равен сумме расходов.
Аналогия – параллельное соединение сопротивлений, напряжение одинаково, а токи суммируются.
![]() Зависимость напора от
расхода H
f Q
называется расходной характеристикой участка трубопровода. Она может быть
получена аналитически или с помощью таблиц. Как правило построение расходной
характеристики производится по точкам. Задаются различными значениями расхода и
находят потери напора на данном участке трубопровода. Строят зависимость H f Q,
которая позволяет найти расход по заданному напору.
Зависимость напора от
расхода H
f Q
называется расходной характеристикой участка трубопровода. Она может быть
получена аналитически или с помощью таблиц. Как правило построение расходной
характеристики производится по точкам. Задаются различными значениями расхода и
находят потери напора на данном участке трубопровода. Строят зависимость H f Q,
которая позволяет найти расход по заданному напору.
![]() Для последовательного
соединения трубопроводов расходная характеристика может быть получена как сумма
напоров характеристик отдельных участков. По ней для заданного напора можно
найти расход и напоры на участках трубопровода.
Для последовательного
соединения трубопроводов расходная характеристика может быть получена как сумма
напоров характеристик отдельных участков. По ней для заданного напора можно
найти расход и напоры на участках трубопровода.
Для параллельного соединения трубопроводов расходная характеристика может быть получена как сумма расходов отдельных участков. По ней для заданного напора можно найти расходы в ветвях и суммарный расход.
Часто встречаются случаи, когда по длине трубопровода происходит раздача некоторой части или всего расхода, причем отбор жидкости (воды) потребителями происходит в нескольких сечениях по длине трубопровода. К таким трубопроводам относятся городские и сельские водопроводы, поливные трубопроводы, подающие воду в каждую борозду через отверстия, трубопроводы различных технических систем, в том числе внутрипочвенного и капельного орошения. Собирающие трубопроводы (дренажные коллекторы) работают с увеличением расхода по длине.
Трубопроводы с непрерывной равномерной раздачей воды вдоль пути характеризуются тем, что точки разбора находятся на одинаковом расстоянии друг от друга, а расходы разбора в этих точках одинаковы. При этом удельный путевой расход на единицу длины составляет qo .
![]() Общий (полный) расход
Q0 , поступающий к начальному
сечению трубопровода, состоит из двух:
Общий (полный) расход
Q0 , поступающий к начальному
сечению трубопровода, состоит из двух:
путевого Qпут , который разбирается по длине l , и транзит-
ного Qтр , проходящего через данный участок:
Q0 Qпут Qтр , при этом
Qпут qol .
Определим потери напора hl на таком участке.
В любом сечении на расстоянии x от начала разбора расход
![]() 1 x.
1 x.
Qx Qтр Qпут
l
2 2
![]()
![]() Гидравлический уклон J dxl
QKx2 , откуда dhl
QKx2 dx. Для нахождения поdh
Гидравлический уклон J dxl
QKx2 , откуда dhl
QKx2 dx. Для нахождения поdh
терь напора на длине l интегрируем полученное выражение в пределах от 0 до l :
![]() hl l
Qx22 dx
hl l
Qx22 dx ![]() 12 l
Qx2dx
12 l
Qx2dx
0 K K 0
Раскроем подынтегральное выражение l l 2
0Qx2dx
Qтр Qпут1 ![]() xl
dx
xl
dx
0
l l l 2
Qтр dx2QтрQпут 1 ![]() xl dxQпут2 01
xl dxQпут2 01 ![]() xl
dx
2
xl
dx
2
0 0
2 2 3
Qтр2 l 2QтрQпутl 2QтрQпут ![]() l2l Qпут2 l 2Qпут2
l2l Qпут2 l 2Qпут2 ![]() l2l Qпут2
l2l Qпут2 ![]() 3ll2
3ll2
2 Qпут2 l .
Qтр QтрQпут ![]()
3
Подставляем значение интеграла в формулу для потерь напора
2
2 Qпут
Qтр QтрQпут
![]() hl 2 3 l .
hl 2 3 l .
K
Введем понятие расчетного расхода Qр
2
Qр
Окончательно расчетная зависимость имеет вид H hl
![]() 2
l .
2
l .
K
Расчетный расход больше транзитного, но меньше полного расхода в начале трубопровода.
В практических расчетах для упрощения принимают Qр Qтр 0,55Qпут .
Необходимость определения диаметра трубопровода возникает в задачах проектирования. Один и тот же расход может быть подан через трубопровод большего диаметра с меньшими потерями напора или наоборот. Оптимальный диаметр трубопровода определяется по сопоставлению капитальных и эксплуатационных затрат.
![]() С увеличением диаметра возрастают капитальные
затраты (точнее – амортизационные). Кривая К.
С увеличением диаметра возрастают капитальные
затраты (точнее – амортизационные). Кривая К.
С увеличением диаметра при заданном расходе снижается средняя скорость потока, а с ней и энергия, затрачиваемая на преодоление гидравлического сопротивления. Эксплутационным (прежде всего энергетическим) затратам отвечает кривая Э. Оптимальным является диаметр трубопровода, при котором суммарные затраты (кривая ) минимальны.
На рисунке минимуму кривой отвечает точка А; значит следует подбирать трубопровод, близкий по диаметру к оптимальному: dопт dА .
Заметим, что в учебниках иногда ошибочно определяют dопт как абсциссу точки В
; несмотря на возможную близость в каких-то случаях к dопт , диаметр dВ , отвечающий равенству капитальных и эксплуатационных затрат, вообще говоря никакого интереса не представляет.
Сравнение капитальных и эксплуатационных затрат не всегда возможно из-за отсутствия необходимой информации. На практике используют таблицу рекомендуемых предельных скоростей и предельных расходов (таблица приводится выборочно)
|
Диаметр трубопровода, мм |
Рекомендуемая предельная скорость, м/с |
Рекомендуемый предельный расход, л/с |
|
50 |
0,96 |
1,88 |
|
100 |
1,15 |
9,03 |
|
200 |
1,34 |
42,1 |
|
500 |
1,45 |
284 |
|
1000 |
1,68 |
1280 |
Таблица применима для стальных труб, прокладываемых в центральных и западных районах России. Для районов Сибири и Урала приведенные в таблице расходы и скорости увеличивают на 1015%. Для Южных районов СНГ уменьшают на 10%. Причины: в Сибири и на Урале более дешевая электроэнергия, но большие капиталовложения в строительство трубопроводов в связи с большой глубиной прокладки труб; в южных районах СНГ более дорогая электроэнергия, но меньше затраты на строительство.
Водопроводные сети, по которым вода из водонапорной башни поступает к потребителям, делят на разветвленные (тупиковые) и кольцевые.
![]() Разветвленные
трубопроводы состоят из основной магистрали и отходящих от узлов сети
ответвлений, которые могут состоять из одной линии (простые ответвления) или
Разветвленные
трубопроводы состоят из основной магистрали и отходящих от узлов сети
ответвлений, которые могут состоять из одной линии (простые ответвления) или
нескольких участков трубопрово-
дов (сложные ответвления).
![]() Городские водопроводы
обычно выполняются в виде кольцевых сетей обеспечиваются водой от двух и более
водонапорных башен Б. В узлах 1-9 находятся потребители (например жилые
массивы, пред-
Городские водопроводы
обычно выполняются в виде кольцевых сетей обеспечиваются водой от двух и более
водонапорных башен Б. В узлах 1-9 находятся потребители (например жилые
массивы, пред-
приятия и т.п.)
Кольцевая сеть позволяет осуществлять водоснабжение всех потребителей в случае аварии или ремонта отдельных участков водопроводной сети. При этом, конечно, потребности в воде будут удовлетворяться не полностью, а , например, на несколько часов в сутки, причем иногда обеспечиваются лишь нижние этажи зданий и т.п., но все же водоснабжение не буден отключено полностью на все время ремонта, что может произойти, если сеть тупиковая.
Строительными нормами и правилами рекомендуется обеспечить пьезометрический напор не менее 10 м при одноэтажной застройке, добавляя 4 м на каждый этаж.
Определить расход жидкости, протекающей по разветвленному трубопроводу в пункты 1 и 2 (истечение в атмосферу). Напор в резервуаре постоянен и известен. Длины и диаметры отдельных участков трубопровода известны. Кинематическая вязкость жидкости и абсолютная эквивалентная шероховатость известны. Местными потерями напора и скоростным напором пренебречь.
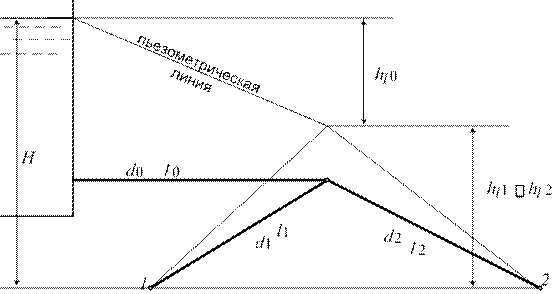
Примечание.
1. Как правило задается не кинематическая вязкость, а вид жидкости и рабочая температура. Кинематическую вязкость берут по таблицам в справочниках.
2. При истечении в атмосферу не потерь на вход в бак, однако в точных расчетах необходимо учитывать скоростной напор выходящей из трубы жидкости. Если им пренебречь и не учитывать местные потери, то весь располагаемый напор равен сумме потерь напора по длине в общем трубопроводе и в разветвленной части (в двух трубопроводах разветвления напор одинаков, однако длины и/или диаметры различны, а значит различны средние скорости и расходы). Решение.
В разветвленном трубопроводе сохраняется баланс расходов Q0 Q1 Q2 .
Неизвестны два расхода, третий находится по балансу. Потери в ветвях разветвляющейся части одинаковы, т.е. hl1 hl2. Располагаемый напор H hl0 h1. Потери в каж-
2
![]() дом
трубопроводе рассчитываются по формуле Дарси-Вейсбаха hli i dli 2ig .
дом
трубопроводе рассчитываются по формуле Дарси-Вейсбаха hli i dli 2ig .
i
2
![]() li Qi .
li Qi .
Расход по участку Qi Fii . Площади Fi известны. Тогда hli i di 2gFi2
В первом приближении примем, что режим движения жидкости в трубопроводе турбулентный, квадратичная область сопротивления (в дальнейшем это утверждение будет уточнено). Коэффициент Дарси для каждого диаметра может быть определен по формуле 0.25
![]() i 0.11э .
Потери в каждом участке трубопровода могут найдены
i 0.11э .
Потери в каждом участке трубопровода могут найдены
Шифринсона
d
через его расходную характеристику, при чем последняя не берется из таблиц, а определя-
Q
![]()
![]() 2 . Здесь расходная
характеристика 2gdi .
2 . Здесь расходная
характеристика 2gdi .
ется аналитически. hi Kii2 li Ki Fi i
Получим шесть уравнений с шестью неизвестными (расходы и потери напора в участках)
2 2 2
Q
h0 02 l0 , h1 Q12 l1, h2 Q22 l2, Q0 Q1 Q2 , h1 h2,
K0 K1 K2
H h0 h1.
Несложные алгебраические преобразования приводят к следующим результатам:
![]()
![]() K2 Q0 Q1 Q2
K2 Q0 Q1 Q2
Q1 Q2 Q1
K1
Уточнение полученных результатов производится в следующей последовательности. Находят средние скорости во всех участках трубопровода, числа Re. Определяют область гидравлического сопротивления, в которой работает каждый участок, и по соответствующим эмпирическим формулам (Блазиуса, Альтшуля, Шифринсона и др.) вычисляют значе-
Ki и ние коэффициента Дарси. Уточняют значения расходных характеристик участков вновь вычисляют расходы по участкам. Такой способ позволяет получить решение с любой требуемой точностью.
Задаются начальным приближением по скорости. Пусть, например 2 м/с по участку 1.
Скорость по участку 2 определяют из простой пропорции (равенство потерь по длине при одинаковом коэффициенте Дарси.
![]() 2
1
l1d2 .
2
1
l1d2 .
l2d1 Находим расход по участкам и общий расход а также скорость на участке 0.
На каждом участке находим число Re, определяем область сопротивления и по соответствующей формуле находим коэффициент Дарси. Вычисляем потери по длине на каждом участке.
Гидравлическим ударом называется скачкообразное повышение давления в трубопроводе (гидросистеме), вызванное резким изменением скорости жидкости.
Название «гидравлический удар» явление получило потому, что резкое изменение давления может сопровождаться сотрясением трубы и появлением звука, сходного со звуком удара молотком по твердому телу.
В конце IXX века после завершения строительства в Москве Рублевской водонапорной станции участились случаи разрыва труб, заложенных глубоко в земле. Первое время аварии объясняли плохим качеством изготовления водопроводных труб. Однако и после замены разрушенных труб новыми аварии возникали вновь. Это заставило начальника Московского водопровода обратиться за помощью к профессору Н.Е. Жуковскому[11], который в то время являлся членом комиссии, решавшей проблему улучшения водоснабжения в г. Москве.
Н.Е. Жуковским была впервые разработана теория гидравлического удара в трубах, основные положения которой изложены в статье «О гидравлическом ударе в водопроводных трубах» (1898 г.).
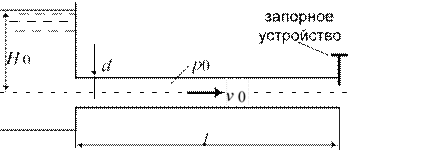
Явление гидравлического удара рассмотрим на примере трубопровода длиной l , диаметром d , в котором под действием напора в баке H 0 движется вода со средней скоростью v 0 . Давление воды p0. На конце трубопровода расположено запорное устройство
(задвижка, кран, клапан и т.д.).
Примем следующие допущения:
– размеры резервуара велики, уровень в нем остается постоянным независимо от явлений, происходящих в трубопроводе.
– начальное давление в трубопроводе практически постоянно и равно p0 gH ;
– движение воды в трубопроводе считаем одномерным, т.е. все местные скорости считаем равными средней скорости, а давление – одинаковыми во всех точках живого сечения. Характеристики такого движения зависят только от продольной координаты;
– потери напора и скоростной напор малы, поэтому пьезометрическая линия практически совпадает с горизонтальной линией. Давление воды p0 практически постоянно по длине трубы
В момент времени t0 затвор мгновенно закрылся.
![]() t 0.
t 0.
Жидкость продолжает двигаться с прежней скоростью. Слои, непосредственно примыкающие к затвору останавливаются (0), давление повышается ( p p0 p ), происходит сжатие жидкости и деформация стенок трубопровода. Кинетическая энергия движущейся воды переходит в потенциальную энергию сжатия воды и деформации стенок резервуара.
Такой процесс распространяется по всей трубе в сторону резервуара со скоростью v уд.
![]() v
v
0 t ![]() l
l
v уд
Процесс повышения давления достиг резервуара.
Мгновенный останов под повышенным давлением
![]() l
l
t ![]() v уд
v уд
Это состояние неравновесное (неустойчивое). В трубе давление повышенное, стенки растянуты. Начинается процесс выхода воды обратно в резервуар, снижения давления до первоначального. Потенциальная энергия переходит в кинетическую. Процесс распространяется в сторону запорного устройства со скоростью v уд.
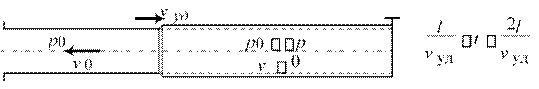
![]() Процесс восстановления давления достиг запорного
устройства. Деформаций нет. Скорость направлена от запорного в бак. 2l
Процесс восстановления давления достиг запорного
устройства. Деформаций нет. Скорость направлена от запорного в бак. 2l
t ![]() v уд
v уд
Инерция движущейся массы воды приведет к понижению давления у запорного устройста. Предполагается, что не происходит нарушения целостности столба воды. Происходит постепенная остановка жидкости и деформация стенок трубопровода. Такой процесс распространяется по всей трубе в сторону резервуара со скоростью v уд.
![]() v
v
t ![]() v уд
v уд
Процесс понижения давления достиг резервуара.
![]() Мгновенный
останов под пониженным давлением 3l
Мгновенный
останов под пониженным давлением 3l
t ![]() v уд
v уд
Это состояние неустойчиво. В трубе давление ниже, чем в резервуаре, стенки сжаты. Начинается процесс входа воды в трубопровод, повышения давления до первоначального и устранения деформации трубопровода. Потенциальная энергия переходит в кинетическую. Процесс распространяется в сторону запорного устройства со скоростью v уд.
![]() v
v
t ![]() v уд
v уд
![]() Процесс восстановления давления достиг запорного
устройства. Деформаций нет. Скорость направлена из бака в сторону запора. 4l
Процесс восстановления давления достиг запорного
устройства. Деформаций нет. Скорость направлена из бака в сторону запора. 4l
t ![]() v уд
v уд
Цикл завершен. Восстановлено начальное состояние (см. t 0). Процесс повторяется. В реальных условиях колебания постепенно затухают.
Определения.
Гидравлический удар –явление резкого изменения давления, возникающее при напорном движении жидкости в трубе вследствие быстрого изменения скорости в одном из сечений.
Скорость ударной волны – скорость распространения волны изменения давления вдоль трубопровода. Фаза удара – время, за которое волна изменения давления проходит весь трубо-
2l
провод и возвращается обратно.
![]() .
Различают фазу повышенного давления и фазу v уд
.
Различают фазу повышенного давления и фазу v уд
пониженного давления.
Положительный гидравлический удар – начинается с фазы повышения давления. Нами рассмотрен положительный гидроудар, задвижка в конце трубопровода.
Отрицательный гидравлический удар – начинается с фазы понижения давления. Если резко закрыть задвижку в начале трубопровода, то произойдет аналогичный процесс скачкообразного изменения давления, однако он начнется с понижения давления за задвижкой. То же происходит при резкой остановке насоса.
Надо найти повышение давления при гидравлическом ударе p , именно оно приводит к разрушению трубопровода. Пусть гидравлический удар вызван резким уменьшением средней скорости в трубопроводе от v 0 до v . Здесь мы изучаем более общий случай – не полной остановки жидкости, а лишь резкого снижения скорости.
![]() v Запорное
устройство находится справа.
v Запорное
устройство находится справа.
Оно резко прикрыто (не закрыто полностью).
Волна повышения давления движется справа налево со скоростью v уд и за
время t проходит расстояние х .
Первоначальная скорость жидкости v 0 уменьшается до v , что приводит к повышению давления на величину p от p0 до p0 p .
Применим к массе жидкости в участке трубы х теорему об изменении количества движения в проекции на ось x . Изменение количества движения равно импульсу внешних сил.
Здесь m – масса воды, заключенная в участке трубы длиной х до прохождения через этот участок ударной волны. Объем V x F . Масса m V x F .
Изменение количества движения этой массы вызвано уменьшением скорости от v 0 до v
mv m v v 0.
На левую грань действует сила Pлев p0F , на правую грань Pправ p0 pF .
Запишем уравнение x F v ![]() 0
p F t
0
p F t
x
Выразим повышение давления p v 0 v ![]()
t
x
Путь на время – это скорость
распространения ударной волны ![]() v уд
v уд
t Получаем формулу
Формула Жуковского для по-
p v0 v v уд вышения давления при гидравлическом ударе.
Повышение давления при гидроударе пропорционально плотности жидкости, изменению ее скорости (v 0 - начальная скорость v -конечная скорость, задвижка не полностью закрыта) и скорости распространения ударной волны, которая, в свою очередь, зависит от свойств жидкости и трубопровода (см. ниже).
Максимальное повышение давления будет при быстрой полной остановке потока v 0:
pмакс v0v уд
Если v v0, то p 0, повышения давления не происходит, гидроудара нет.
![]() v
v
Определим скорость распространения ударной волны в упругом трубопроводе круглого поперечного сечения. Рассмотрим отсек длиной x , через который проходит ударная волн за время t .
В течение времени t жидкость одновременно втекает слева и вытекает справа, но с разными скоростями. Поступление через левую грань происходит со скоростью v 0 , одновременно через правую грань жидкость выходит с меньшей скоростью v . За время t в рассматриваемый отсек войдет дополнительный объем жидкости V F v 0 v t .
Этот вошедший объем займет пространство, образовавшееся вследствие растяжения стенок трубопровода V1 и за счет сжатия жидкости в отсеке V2, т. е. V V1 V2
При растяжении стенок радиус трубы станет равным r0 r , площадь увеличится на величину F . Тогда V1 F x .
При повышении давления на величину p первоначальный объем жидкости в отсеке Fx уменьшится на величину V2 pF xp. Здесь p – коэффициент объемного сжатия (см. «Свойства жидкостей», «Сжимаемость»). Величина обратная коэффициенту
объемного сжатия – модуль упругости жидкости. Eж ![]() . Получим V2
. Получим V2 ![]() .
.
p Eж
Имеем V
V1 V2 . Подставляем F v 0 v t
F x ![]() F x p .
F x p .
Eж
![]() Разделим
на объем отсека Fx , получим v 0 v .
Разделим
на объем отсека Fx , получим v 0 v .
x F Eж
![]() p Ранее получено p v0 v v уд , откуда v0 v .
p Ранее получено p v0 v v уд , откуда v0 v .
x p F p
![]()
![]()
![]() Очевидно,
что v уд . Получим: 2
F
Eж .
Очевидно,
что v уд . Получим: 2
F
Eж .
![]() t v уд
t v уд
Отсюда v уд . Перейдем к пределу при t 0 vуд .
Приведем полученную формулу к удобному для использования виду.
2 2rdr dr
dF d(r )
![]() Из
геометрических соображений 2 .
Из
геометрических соображений 2 .
F r2 r2 r
Считаем, что модули упругости материала стенки трубопровода Eст и жидкости Eж не зависят от давления.
![]()
![]() [12]
, в наших обозначениях dr
d
.
[12]
, в наших обозначениях dr
d
.
Деформации подчиняются закону Гука
r0 Eст
Напряжение в стенке трубы, вызванное действием давления («котельная» формула) pD
![]() .
Здесь D – диаметр
трубопровода,
– толщина стенки.
.
Здесь D – диаметр
трубопровода,
– толщина стенки.
D
![]()
![]() Перейдем
к приращениям d dp. 2
Перейдем
к приращениям d dp. 2
. Умножаем числитель и знаменатель на Eж .
t F p
v уд
 Формула Н.Е.
Жуковского для скоростраспространения ударной волны и
Формула Н.Е.
Жуковского для скоростраспространения ударной волны и
Здесь Eж и Eст – модуль упругости жидкости и материала стенки трубопровода.
Модуль упругости для воды Eводы=2*103 МПа, для стали на два порядка выше Eстали
2,1*105 МПа, для минеральных масел немножко меньше, чем у воды, зависит от вязкости. D – внутренний диаметр трубы, – толщина стенки трубопровода.
![]() Величина
Eж
aж – скорость звука в
жидкости.
Величина
Eж
aж – скорость звука в
жидкости.
Для воды скорость звука, т.е. скорость распространения звука в воде aводы=1425 м/с, для бензина 1200 м/с, для минеральных масел того же порядка. Скорость распространения звука в воздухе 340 м/с.
Время закрытия запорного устройства влияет на повышение давления при гидроударе.

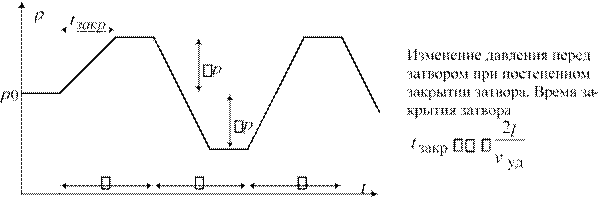
t0
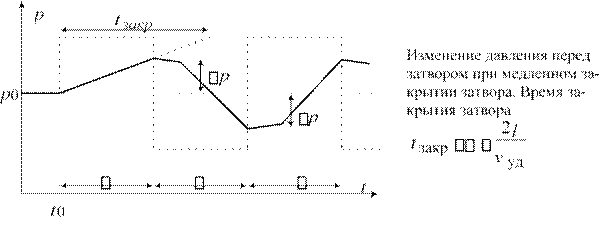
Определения. Прямой гидроудар – время полного закрытия задвижки меньше продолжительности
2l
фазы гидроудара. tзакр
![]() .
p v0v уд
v уд
.
p v0v уд
v уд
Непрямой гидроудар – время полного закрытия задвижки больше продолжительности
2l
фазы гидроудара. tзакр ![]() . pмакс
v 0v уд
. pмакс
v 0v уд ![]() .
.
v уд tзакр
Рекомендации Н.Е. Жуковского из его работы «О гидравлическом ударе в водопроводных трубах»
«Простейшим способом ограждения водопровода от гидравлических ударов является приспособление к медленному закрытию кранов. При этом продолжительность закрытия должна быть пропорциональна длине труб. Воздушные колпаки надежных размеров, поставленные при кранах и задвижках, почти совершенно уничтожат гидравлический удар».
1. Медленное закрытие запорного устройства (видно из формулы для непрямого удара)
В лабораторных работах №1 и №6 имеется пробковый кран, а в лабораторной работе № 3 шаровой клапан. При быстром их закрытии происходит гидравлический удар и вода выплескивается из пьезометров и обливает шкалу. Поэтому закрывать надо медленно.
При испытаниях центробежного насоса при быстром закрытии шарового крана слышен хлопок, это гидроудар (при быстром закрытии водопроводного крана иногда возникает вибрация труб).
2. Применение предохранительных клапанов прямого действия (гидроклапана давления Г54 – в гидроприводе)
3. Применение специальных защитных клапанов.
В ответственных трубопроводах для недопущения гидравлического удара используются специальные устройства. При закрытии запорного устройства от повышения давления перед ним приоткрывается перепускной клапан и жидкость обводится.
4. Использование гидро- пневмо- аккумуляторов.

5. Увеличение толщины стенок, чтобы труба выдержала повышение давления, вызванное гидравлическим ударом.
Гидравлический таран – неэнергоемкий механизм для подъема воды.
Гидравлический таран состоит из ударного клапана 1, нагнетательного клапана 2, воздушного колпака 3. Через питающую трубу 4 таран соединяется с бассейном 5, через нагнетательный трубопровод 6 – с приемным резервуаром 7.
Представим, что в начальный момент времени нагнетательный и ударный клапаны закрыты, избыточное давление в воздушном колпаке pк gH 2, а вода в питающей трубе 4 неподвижна. Для того, чтобы таран начал автоматически работать необходимо один раз открыть ударный клапан 1.
Через клапан 1 происходит истечение воды, скорость которой вследствие инерции воды, находящейся в питающей трубе 4, постепенно увеличивается. С увеличением скорости истечения сила, действующая на клапан 1 снизу вверх, также увеличивается и, как только она превышает вес самого клапана, он резко закрывается. Происходит гидравлический удар. Давление в трубе 4 перед нагнетательным клапаном 2 повышается, клапан 2 открывается и вода под повышенным давлением поступает в воздушный колпак 3, сжимая в нем воздух, и через нагнетательный трубопровод 6 в приемный резервуар 7. Волна повышения давления, вызванная гидравлическим ударом при закрытии клапана 1, движется по трубопроводу 4 до резервуара 5, вызывая остановку воды в этом трубопроводе. Когда обратная вона понижения давления достигает камеры перед нагнетательным клапаном 2, этот клапан закрывается, но автоматически открывается клапан 1. Начинается новый цикл (читай абзац сначала).
Таран работает автоматически. Он использует энергию падающей воды для подъема части этой воды на необходимую высоту.
Если через Q1обозначить расход воды, сбрасываемый через ударный клапан 1, а через Q2 – расход воды, поступающий в приемный резервуар, то коэффициент полезного
![]() Q2H 2 .
Высота H2 (2...10)H1. При действия гидравлического
тарана
Q2H 2 .
Высота H2 (2...10)H1. При действия гидравлического
тарана
Q1 Q2H1
этом расход Q2 (0,4...0,07)Q1. 0,85...0,2. Вода подается на высоту до 40 метров.
Надо отметить, что работа гидравлического тарана сопровождается большими непроизводительными потерями воды.
На одном графике строим расходные характеристики участков 1 и 2. Эти участки соединены параллельно, суммарная характеристика строится путем суммирования расходов при одинаковом напоре (кривая 1+2). На этом же графике строим характеристику участка 0. Этот участок соединен с участком 1+2 последовательно, суммарная характеристика всего трубопровода строится суммированием напоров при одинаковом расходе (кривая ). По заданному суммарному напору H * по кривой находим расход через весь трубопровод и через участок 0. (Линия H *-a-b-c-Q0 .) Точке b соответствует напор на участках 1 и 2, точке с напор на участке 0. Пересечение горизонтали через точку b с характеристиками трубопроводов 1 и 2 определяет расходы в них. (Линии b-d-Q1 и b-e-Q2 .)
Рассмотренный графоаналитический способ расчета не дает точного решения, однако позволяет разработать алгоритм его нахождения с использованием средств вычислительной техники.
Тема 2.1. Основы термодинамики
Тема 2.2. Законы термодинамики
Тема 2.3. Идеальные газы
Тема 2.4. Термодинамические процессы и циклы
Тема 2.5. Термодинамика потоков
Тема 2.6. Термодинамический анализ теплотехнических устройств
Раздел 2. Термодинамика
Тема 2.1. Основы термодинамики
Возникновение термодинамики было связано с потребностью объяснения, предсказания и расчета макроскопических процессов, происходящих в газах и жидкостях при различных внешних воздействиях на них. При этом данная потребность была вызвана, прежде всего, попытками создания различных теплотехнических устройств, в частности, тепловых машин.
Работа тепловых машин как устройств, с помощью которых совершается механическая работа за счет тепловой энергии, не может быть описана в рамках макроскопической механики, так как в таких машинах происходят тепловые процессы, связанные с микроскопическим движением частиц рабочего тела. Для адекватного описания этих процессов возникла необходимость создания термодинамики, как самостоятельного раздела физики.
История возникновения термодинамики наложила отпечаток на используемую в ней терминологию, которая в достаточно большой степени была позаимствована из теплотехники. Такие понятия как температура, количество теплоты, теплоемкость и др. первоначально были введены для описания процессов в различных тепловых машинах и устройствах, но строгое количественное определение этих величин было дано только после создания термодинамики.
Поскольку в период становления термодинамики молекулярная структура вещества являлась научной гипотезой, термодинамика вынуждена была опираться на постулаты, основанные на макроскопических свойствах вещества. Эти постулаты, являющиеся основными законами термодинамики, получили названия начал термодинамики. Их три и все они имеют своим основанием опыт. Кроме того, нулевым постулатом можно считать утверждение о существовании равновесного состояния термодинамической системы и физической величины – температуры, необходимой для количественного описания такого состояния. Область применения термодинамики соответствует области, в которой справедливы постулаты термодинамики.
Термодинамика – раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений, а основывается на двух началах термодинамики – фундаментальных законах, установленных экспериментальным путем.
Статистические методы физики не могут быть использованы во многих разделах физики и химии, тогда как термодинамические методы универсальны. Однако статистические методы позволяют устанавливать микроскопическое строение вещества, тогда как термодинамические методы лишь устанавливают связи между макроскопическими свойствами. Молекулярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое, но отличаясь методами исследования.
Всякий материальный объект, состоящий из большого числа частиц (молекул, атомов, ионов), условно отделяемый от окружающей среды, является термодинамической системой. Это может быть кристалл минерала, раствор любого вещества в какой-либо емкости, газ в баллоне, отдельная клетка организма или организм в целом. При взаимодействии системы с окружающей средой она может получать или отдавать энергию в виде тепла или работы. Так, горячий кусок металла, охлаждаясь, отдает энергию окружающему воздуху. Газ, заключенный в цилиндр, закрытый поршнем, при расширении совершает работу. Кроме того, система может обмениваться со средой веществом в результате, например, диффузии вещества из системы в окружающую среду и наоборот.
В соответствии с различными видами взаимодействия с окружающей средой все системы можно классифицировать следующим образом:
1). Если система не обменивается со средой ни энергией, ни веществом, то эта система называется изолированной. В качестве примера можно привести жидкость в термосе. Эту систему можно считать изолированной на небольших промежутках времени, когда незначительным, но все же имеющим место теплообменом можно пренебречь.
2). Система называется закрытой (замкнутой), если между ней и окружающей средой возможен обмен энергией в виде теплоты и/или работы, но не возможен обмен веществом. Пример – закрытый сосуд с веществом. Искусственные замкнутые экосистемы – еще один интересный пример. В этих рукотворных системах имитируются условия существования организмов в космических кораблях, используется только внешняя энергия, а все необходимые для организмов (включая человека) вещества производятся внутри системы, при этом осуществляется и утилизация отходов в результате замкнутых циклов. Работы с замкнутыми экосистемами в настоящее время активно ведутся в Кэнеди Спейс Центре (США). В 70-х годах прошлого столетия ведущими специалистами в этом направлении считались ученые Института биофизики СО РАН (г. Красноярск).
3). Открытой является система, которая обменивается с окружающей средой и веществом и энергией. Примеры – живые организмы по отношению к окружающей среде, клетка по отношению ко всему организму в целом.
Состояние термодинамической системы определяется физическими характеристиками – массой, объемом, давлением, температурой, составом, теплоемкостью и др., которые называются термодинамическими параметрами. Различают 2 вида параметров – интенсивные и экстенсивные. Экстенсивные параметры пропорциональны количеству вещества системы (объем, масса). Интенсивные параметры не зависят непосредственно от количества вещества (температура, давление, химический потенциал, вязкость, концентрация и т.п.).
При изменении параметров системы изменяется также ее состояние, т.е. в системе осуществляется термодинамический процесс.
При термодинамическом исследовании не требуются знания о характере движения и взаимодействия отдельных частиц. Термодинамика исследует физические свойства систем исходя из условий различных превращений энергий и соотношения между разными видами энергий.
Пусть рассматривается некоторая совокупность объектов (материальных тел). Заключим их в некоторую абстрактную (виртуальную) воображаемую или материальную границу (оболочку). И все, что находится внутри этой границы, назовем термодинамической системой. Выбор центрального для термодинамических расчетов объекта определяет сам исследователь, и он же решает, что собой представляет внешняя (окружающая) среда, с которой это центральное тело взаимодействует.
В технической термодинамике объектом исследования является рабочее тело (газ, жидкость или твердое) как единая макросистема какого-то вещества или смеси веществ.
Взаимодействие термодинамической системы (рабочего тела) с внешней средой, по предположению, осуществляется только на границе. «Взаимодействие – вот главное, когда мы рассматриваем природу в целом» отметил философ и естествоиспытатель Ф. Энгельс.
Взаимодействием термодинамической системы с внешней средой называется акт энергообмена. Есть энергообмен в какой-то форме – значит есть взаимодействие. Иначе, взаимодействия нет. «Добродетельным можно быть самим по себе, а для порока нужны двое» отметил тот же Ф. Энгельс. В частности, если рабочее тело заключено в объем с неподвижными прочными стенками, то внешняя среда не может деформировать (сжимать или расширять) рабочее тело. Тогда в термодинамике говорят, что термодинамическая система деформационно изолирована от внешней среды. Если на границе термодинамической системы расположить толстый слой теплоизоляции, то система не может обмениваться теплотой с внешним миром. (Зимой люди одевают шубы и теплые пальто.) Тогда говорят, что рабочее тело теплоизолировано, а все процессы в нем называют адиабатическими. Аналогично, можно говорить о химическом взаимодействии (физхимия), о электрическом, магнитном, о соответствующей изоляции от внешней среды.
Параметр состояния – физическая величина, т.е. количественная и качественная характеристика свойств или поведения термодинамической макросистемы (рабочего тела). На рассвете развития и становления термодинамики параметры состояния системы избирались на основе прямых измерений в опытах. В современной термодинамике параметры состояния обязательно соотносят с каким-то видом (родом) взаимодействия системы с внешней средой.
Человеческий опыт позволяет различать множество взаимодействий по их роду (типу, виду): деформационное изменение рабочего тела по геометрии объема, поверхности или длины рабочего тела, термическое (нагрев или охлаждение), химическое (молекулы в исходной смеси веществ химически взаимодействуют с образованием молекул новых веществ), электрическое (перемещение зарядов под действием внешнего электрического поля), магнитное (диполи, микро магниты, домены рабочего тела занимают новое положение в пространстве под действием внешнего магнитного поля).
Техническая термодинамика, будучи частью термодинамики вообще, занимается только деформационным и термическим взаимодействиями, происходящими с телами в целом в их массе и объеме (макросистемы).
Потенциал. В любой реальной системе при ее взаимодействии с внешней средой потенциалом называется такой параметр, разность значений которого в системе и внешней среде является первопричиной взаимодействия.
Иными словами, разность потенциалов – необходимое условие взаимодействия (и любого рода энергообмена или массообмена).
Необходимым условием деформации (изменения геометрии и формы рабочего тела) является разность давлений р внутри и вне системы, других причин для деформации объема просто нет. В гидравлике (текучие рабочие тела) эта же разность давлений является причиной движения жидких сред.
Необходимым условием термического взаимодействия системы с внешней средой является разность температур Т внутри и вне системы
Вообще, разность значений внешнего Ре и внутреннего Р потенциала можно назвать «движущей силой».
Итак, – р (минус) – потенциал деформационного взаимодействия. Причина появления минуса рассматривается далее.
Т – потенциал термического взаимодействия.
По определению, давлением р называется отношение силы воздействия к площади поверхности действия силы:
р = f / s, [f] = н (ньютон), [s] = м2. [p] = н/м2. [T] = К (Кельвин).
Координата состояния. Координатой состояния называется такой параметр состояния, который обязательно изменяется при данном роде взаимодействия.
Иными словами, изменение координаты состояния является достаточным условием взаимодействия (т.е. энергообмена или массообмена) системы с внешней средой.
Поиском конкретного вида таких параметров – координат занимается экспериментальная и теоретическая физика в ее различных разделах. Для механического деформационного взаимодействия координатой являются: длина – при линейном воздействии (растягивание пружины, например), площадь – при поверхностном воздействии (выдувании пузырей, например), объем – при воздействии на трехмерное тело, масса – при химическом взаимодействии двух или более веществ (убывание исходных веществ и увеличение количества продуктов реакции).
Для деформационного взаимодействия координатой состояния является геометрический объем V м3, поверхность S м2 или протяженность l м конкретного тела (вещества). Однако геометрические характеристики объема м3, поверхности м2 или длины м ничего кроме абсолютного значения (количества) не дают. Подобные количественные характеристики не могут относиться к параметрам состояния системы (поэтому называются экстенсивными величинами). Для рабочего тела в обобщенном виде параметром состояния, т.е. характеристикой последнего, служит удельное значение геометрической характеристики: удельного объема, т.е. геометрического объема, отнесенного к массе m кг рабочего тела, помещенного в объем V:
v = V / m, м3 / кг
Заметим здесь же, что удельный объем вещества в термодинамической системе очень просто связан с плотностью ρ среды, которая почему-то более привычна студентам:
v ≡ 1 / ρ; ρ ≡ 1/ v кг/м3
Плотность вещества и его удельный объем просто обратно пропорциональны, т.е. vρ
= 1.
Термическая координата состояния и ее экстенсивная величина носит название энтропия, обозначается буквой S, имеет размерность дж/К, а параметром состояния рассматривается удельное значение энтропии, относящееся к интенсивным величинам (характеристикам), оно обозначается буквой S.
s = S / m, дж / кг К
Энтропия рабочего тела – такая же физическая величина, как хорошо знакомые давление, объем, температура. Энтропию также можно измерять в специальном эксперименте или рассчитывать по некоторой методике. Исторически энтропия была введена немецким термодинамиком Клаузиусом аналитическим анализом термодинамических взаимодействий.
Еще и еще раз подчеркнем: координата состояния данного рода взаимодействия никогда не изменяется, если отсутствует этот род взаимодействия.
Тема 2.2. Законы термодинамики
Воздействием внешней среды на термодинамическую систему мы назвали акт обмена энергией между двумя объектами. Поэтому естественной мерой воздействия является количество энергии, которой обменивается система с внешней средой. Формальную запись количества воздействия термодинамика позаимствовала у теоретической механики. В аппарате последней, как и в теории поля, термин потенциал относится к энергии рабочего тела, а не к его параметру.
Элементарным количеством воздействия данного рода называется произведение потенциала на приращение сопряженной координаты.
│dKd│ = pdv, дж/кг, │dKT│ = Tds, дж/кг,
где К – количество воздействия, индексы «d» и «Т» – соответственно деформационное
и термическое воздействие, │ │- символика абсолютного значения величины.
Здесь уместно отметить об отличии направления действия сил и потенциалов. В теоретической механике, которая возникла исторически ранее термодинамики, знак «+» был принят для работы расширения системы (dv > 0). В термодинамике для потока теплоты q от системы во внешнюю среду принимается знак «-« (ds < 0). Соответственно, если теплота подводится к системе из внешней среды, то ее знак принимается «+» и ds > 0.
Это же правило устанавливается строго термодинамически. Для записи в одном уравнении количеств воздействия Кd и КТ обмена системы с окружающей средой следует лишь вспомнить качественную связь между направлением действия движущей силы и изменением координаты. Действительно, при силовых взаимодействиях Xe > X (dX > 0) координата убывает (dx < 0), т.е. dK < 0 (знак минус). При потенциальных взаимодействиях для Ре > Р (dP > 0) координата возрастает и количество внешнего воздействия должно входить в уравнение со знаком «+». Иными словами, формально потенциал это минус сила.
Внутренней энергией термодинамической системы называется сумма всех видов энергии в системе.
В школьном курсе физики различают два вида энергии: кинетическая и потенциальная. Под кинетической энергией понимают энергию движения конечного количества массы макротела в геометрическом пространстве. При этом различают движение поступательное, как движение центра масс, движение вращательное вокруг какой-то оси и движение колебательное, как перемещение частей массы относительно друг друга.
Разумеется, внутренняя энергия возрастает или убывает за счет потоков через границу рабочего тела (за счет количеств внешних воздействий между системой и внешней средой). Именно подобные энергетические преобразования по существу между каким-то внешним телом и рабочим телом увеличивают или уменьшают внутреннюю энергию. В самом веществе рабочего тела происходят структурно-энергетические преобразования. Последние адекватны роду (виду) взаимодействия. Если это электрические импульсы (за счет разности электрических потенциалов ΔV), то в системе происходит движение зарядов. Если воздействие на рабочее тело тепловое, то интенсифицируется движение молекул (растет их кинетическая энергия) и т.д.
Однако, термодинамика не занимается таким детальным рассмотрением роли и влияния на вещество видов энергии – это задача физики и физической химии. Обозначение внутренней энергии в термодинамике – U дж или u = U/m дж/кг.
На специфическом языке термодинамики это просто закон сохранения энергии в замкнутой системе: изменение внутренней энергии термодинамической системы равно сумме количеств внешних воздействий.
Аналитическая запись закона (основное уравнение термодинамики:
dU = ∑ δKi или dU = δQ – δW = T dS – p dV.
для термодеформационной системы. Приращение внутренней энергии dU записано
через параметры состояния р,V,Т,S, т.е. через потенциалы и координаты двух видов взаимодействия. В интенсивной форме запись первого закона термодинамики имеет вид: dq ≡ T ds, dw ≡ p dv и тогда du = dq – dw = Tds – pdv.
Здесь dq = Tds – элементарное количество теплоты, подведенное (отведенное) к системе, т.е. это элементарное количество термического воздействия, dw = pdv – элементарное количество работы деформации (механической работы), т.е. элементарное количество деформационного воздействия.
Замечание. В уравнении первого закона (основного закона термодинамики) в правой части входят внешние воздействия, т.е. при потенциальных воздействиях Pedxe и силовых –Xedxe, т.е.
dU = ∑Pedxe - ∑Xedxe
Если изучаются равновесные (квазистационарные) процессы, в которых нет отличия по величине сил (Х) и потенциалов в системе (Р) и окружающей среде (Ре), т.е. между ними бесконечно малая разница по величине, то все переменные основного уравнения термодинамики – функция U и аргументы P,X,x относятся к исследуемому рабочему телу. Действительно, из dU = ∑Pedxe - ∑Xedxe при Pe – P = ΔP и Xe – X = ΔX получим dU = ∑(P +ΔP)dx - ∑(X + ΔX)dx,
и при ΔР → о(ΔР) и ΔХ → о(ΔХ) окончательно с учетом равенства │dxe│ = │dx│получаем dU = ∑ δKi или dU = δQ – δW = T dS – p dV и dq ≡ T ds, dw ≡ p dv и du = dq – dw = Tds – pdv
Окончательно, основное уравнение технической термодинамики, изучающей квазистатические (равновесные) процессы имеет вид: du = Tds – pdv
Подведем предварительные итоги. Выше представлены основные определения понятий термодинамики, их необходимо запомнить, чтобы говорить на языке термодинамики. Взаимосвязь понятий иллюстрирует схема на рисунке Схема последовательности ввода и взаимосвязей понятий в термодинамике.
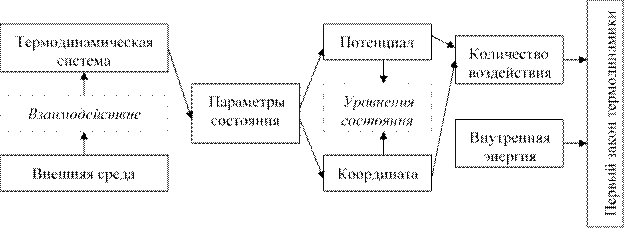
Рис. 2.1. Схема последовательности ввода и взаимосвязей понятий в термодинамике
Уравнением состояния рабочего тела называется функциональная зависимость потенциала от всех координат состояния.
Следовательно, сколько родов взаимодействия термодинамической системы с внешней средой, столько потенциалов, столько координат состояния и столько уравнений состояния.
Для термодеформационной системы (т.е. для двух родов взаимодействия: термического и деформационного) уравнений состояния два, т.к. два потенциала в соответствии с du = Tds – pdv:
p = f(s,v), T = φ(s,v)
Конкретный вид функций f(s,v) и φ(s,v) предоставляют для термодинамики физики, которые для этого проводят специальные теоретические и экспериментальные исследования. Полученные соотношения параметров состояния системы четко отражают физические связи внутри рабочего тела (системы) – первичными сигналами изменения состояния являются координаты. Сами соотношения относятся к уравнениям состояния – это общий вид такого уравнения в термодинамике.
В силу исторических обстоятельств развития физики и термодинамики уравнение состояния идеального газа не содержит энтропию: pv = RT (уравнение Клайперона – Менделеева или уравнение Клайперона[13])
где R = 8314/μ. Здесь 8314 дж/кмольК – универсальная газовая постоянная, μ – моле-
кулярный вес вещества рабочего тела, кг/кмоль. Это уравнение было получено из опытов с газами при невысоких давлениях и температурах. Разумеется, из p = f(s,v), T = φ(s,v) обе аналитические связи можно свести к одной F(p,v,T) = 0, которая не противоречит экспериментальному pv = RT. Этим не исчерпывается роль термодинамики в решении проблемы уравнений состояния. Она накладывает существенные ограничения на функциональный вид этих функций. Эти функции могут быть не любыми, а обязательно удовлетворять условиям:
(∂f/∂v)s ≡ (∂(-p)/∂v)s ≥ 0 и (∂φ/∂s)v ≡ (∂T/∂s)v ≥ 0
В этой записи, а мы будем ею широко пользоваться в дальнейшем, индекс внизу справа у скобки с частной производной означает, что соответствующий параметр состояния фиксирован.
Эти неравенства обычно называют критерием стабильности термодинамики, в химии – это формальная запись принципа ле Шателье – Брауна, хорошо знакомого студентам химико-технологического профиля образования.
Происхождение критерия стабильности термодинамики – эмпирический факт. Многочисленные наблюдения за различными термодинамическими системами показывают, что с ростом координаты состояния какого-то рода взаимодействия (и отсутствия других видов) соответствующий потенциал самопроизвольно не убывает (т.е. растет или неизменен). Обратно, с увеличением потенциала сопряженная координата состояния самопроизвольно также не убывает (т.е. растет или неизменна)
Для теплоизолированной системы (s = const) c увеличением удельного объема, согласно критерию стабильности, давление в системе только уменьшается, но это и очевидно. Для деформационно изолированной системы (v = const) с увеличением энтропии температура газа обязательно увеличится, и обратно, с увеличением температуры энтропия только увеличится. Действительно, если закрытый газовый баллон с каким-то газом положить в костер, то температура газа обязательно увеличится в согласии с критерием стабильности. Вот такие и многие другие экспериментальные факты термодинамика «присвоила» себе.
Измерение или расчет каких-либо характеристик рабочего тела относятся к количественной оценке величины этих характеристик по сравнению с эталоном самой величины. Подобные эталоны приняты в международной практике при введении стандартов на сами характеристики и их эталоны. В настоящее время действует, как обязательный, международный стандарт (SI) или Российский (СИ), утвержденный в 1980 году как обязательный для всех отраслей науки и техники. Основных единиц в этом стандарте – 6 и это: длина – метр, масса – килограмм, термодинамическая температура – градус Кельвина, сила тока – ампер, сила света – свеча, время – секунда. Все они используются в различных разделах термодинамики. В производные единицы включены термодинамические величины: сила – ньютон (Н), давление – (Н/м2), работа и количество теплоты – джоуль (дж).
Из курса физики известно, что производные величины представляют результат взаимодействия двух или более физических объектов в пространстве или во времени. Характеристика и размерность производных величин отличаются от таких же для исходных взаимодействующих объектов, а размерность первых определяется по уравнениям законов связи вторых. Так работа – это произведение действующей силы на путь, т.е. производная величина определяется по уравнению W = X*x, в котором сила Х выражается в избранной системе единиц. Но вне зависимости от системы единиц понятие силы едино согласно второму закону Ньютона – это произведение массы тела на ускорение его Х = mа. Тогда для обязательной в употреблении системе СИ получим [X] = 1 кг*1 м/с2 = 1кг м/с2 и эта сила называется Ньютон, т.е. 1 Н = кг м/с2.
В технической системе единиц, встречающейся в учебниках и старых проектах производств, принята иная единица силы – кГ – килограмм силы, полученная из того же уравнения второго закона Ньютона для массы 1 кг и ускорения силы тяжести g = 9,81 м/с2 (точнее 9,80665). Очевидна связь между этими двумя единицами силы: 1 кГ = 9,81 Н. Соответственно работа в технической системе единиц вычисляется по величине (количеству) в кГм, а в системе СИ в Нм, названной джоулем (дж). Размерность последней величины кгм2с-2 и она же используется для расчетов количества теплоты Q, которая в технической системе единиц имеет единицу – Ккал или кал. Согласно закону эквивалентности 427 кГм работы эквивалентны 1 Ккал, т.е. 1 ккал = 4,19 кдж.
Размерность давления по определению – сила, отнесенная к единице поверхности действия силы: н/м2 = кг/мс2. Единица давления н/м2 = П названа паскаль. Но, оказалось, в технике используются много большие давления, чем паскали. Поэтому введена величина 1 бар = 105 П, которая удобно соответствует технической единице – одной технической атмосфере, равной 104 кГ/м2 или 0,981*105 П.
Прямые измерения абсолютного давления, как параметра состояния рабочего тела, невозможны чисто технически. Косвенные измерения всегда связаны с применением приборов, замеряющих разность давлений, – манометров. В производственных условиях применяются механические или тензометрические манометры, а при давлениях в аппаратах ниже атмосферного или немного выше его используются жидкостные манометры, чаще всего так называемые U-образные дифманометры. Они представляют собой две вертикальные параллельные стеклянные трубки, соединенные внизу перемычкой, коленом из самой трубки. В таком приборе вес столба жидкости h выравнивается разностью давлений Δр внутри аппарата и в атмосфере (рис.2). В аналитической форме:
Δр =ρgh н/м2,
где ρ – плотность жидкости, залитой в U-образный манометр, кг/м3, g = 9,81 м/с2 –
ускорение свободного падения, h – разность столбов жидкости в коленах U-образного манометра. Легко видеть, что р = h + В,
где В – барометрическое давление. В этом уравнении все величины, естественно, приведены к одной размерности. Заметим, что величина В – давление в атмосфере по отношению к глубокому (космическому) вакууму.
При наличии в аппарате среды под разряжением (под вакуумом) столб жидкости в Uобразном манометре вместе с остаточным давлением газа в аппарате будут уравновешены атмосферным давлением:
p + h = B,
т.е. само абсолютное давление будет рассчитываться по прежним переменным p = B – h.

Рис. 2.2. Иллюстрация к измерению давления.
Здесь р – давление в сосуде, h - разность столбов жидкости в U-образном манометре.
В сечении а – а давления в трубках справа и слева уравновешены.
Подчеркнем еще раз – параметром состояния является лишь абсолютное давление, которое отсчитывается от безуслов0ного нуля, т.е. природного абсолютного начала отсчета (космосе). В земных (технических) условиях договорились об абсолютной шкале давлений согласно закону Шарля: р = р0(1 + βТ) или Δр/р0 = βТ.
Здесь из опытов получено для идеальных газов β = 1/273.
Температурная шкала создается следующим образом. Для любого идеального газа выполняется уравнение состояния в виде:
pV = F(θ),
где F(..) – универсальная функция температуры. Опыт показывает, что эта функция линейно растет с ростом температуры: θ = αpV + β,
где α и β – константы. Тогда для температуры плавления льда и температуры кипения воды (при давлении 105 Па) в градусах Цельсия запишем:
0 = α(pV)0 + β, 100 = α(pV)100 + β
Система уравнений (4.2) относительно α и β легко решается, и это решение подставим в (4.1). Получим: θ = 1000C * (pV –(pV)0)/((pV)100 – (pV)0)
Из опыта известно, что для идеального газа
(pV)100 / (pV)0 = 1,366
Подставляя это соотношение в (4.3), получаем pV = (pV)0 (1 + 0,00366θ) Здесь величина θ есть «идеально-газовая температура». Величина pV, равная универсальной функции температуры, станет равной 0, если θ = θ0 = -1/0,00366 = -273,150С. Если перенести начало отсчета температуры θ из 00С в точку θ0, то получим Т(К) = θ – θ0 = (θ + 273,15) К.
Так получается шкала термодинамической (абсолютной) температуры Т в кельвинах, зная эмпирическую шкалу температуры Цельсия. Часто вместо θ используют обозначение t, одновременно для практических расчетов пренебрегают величиной 0,15 на фоне 273. Таким образом
T = t + 273, Где температура Т в кельвинах, а температура t в Цельсиях.
В англо-язычной научно-технической литературе часто встречается понятие температуры по шкале Фаренгейта. Связь этой шкалы со шкалой Цельсия следующая:
t0F = 9/5 (t0C + 32) или t0C = 5/9 (t0F – 32)
Параметры состояния в термодинамике являются макрохарактеристиками системы, т.е. они определяют свойства и поведение системы в целом, а не свойства и поведение ее частей, не внутренних составляющих системы. Термодинамика занимается только макросистемами.
В предыдущей главе по существу изложена аксиоматика термодинамики, ее базис, фундамент. Так, собственно, поступали Евклид, Лобачевский, Риман, создавая свои «математики». Однако, для свободного и глубокого владения методом термодинамического анализа необходим широкий спектр физических представлений, образов, ассоциаций, связанных с основными понятиями термодинамики.
Как же представляет себе статистическая физика параметры состояния в термодинамике? По существу, сказать: «Параметры состояния – это макрохарактеристика объекта», сказать: «Термодинамика занимается макросистемами» – означает, на языке теории вероятностей и статистики, что параметры состояния в термодинамике являются просто средними величинами, математическим ожиданием некоторых случайных величин.
Удельный объем v м3/кг.
Рассмотрим некоторый фиксированный геометрический объем V, м3 какого-то газа с границей Г. Пусть этот объем находится в том же газе, а стенки границы Г абсолютно проницаемы для молекул газа.
Рис. 2.3. Иллюстрация к понятию удельного объема
Молекулы совершают случайное, хаотическое блуждание, какие-то из них войдут в объем V через границу Г, а какие-то выйдут из объема. Следовательно, число молекул в объеме V является случайной величиной с каким-то математическим ожиданием, т.е. средним значением. Если это среднее значение умножить на массу молекулы и произведение разделить на V, то и получим, по определению, величину плотности ρ. И в соответствии с (1.3) далее получаем величину удельного объема v. Отметим важное обстоятельство: чем больше число молекул газа в V, тем точнее находится оценка среднего значения числа молекул в V. Именно в этом смысл макрорассмотрения: число молекул газа должно быть очень большим. Что такое v или ρ, если в объеме V «бегает» одна – две молекулы – не знает никто.
Давление р н/м2.
Рассмотрим газ и непроницаемую стенку (рис. 2.4).
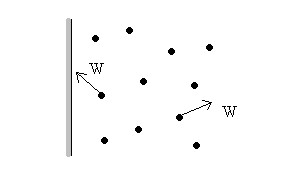
Рис. 2.4. Иллюстрация к понятию давления р
Молекулы газа беспорядочно движутся в объеме около стенки. Скорость их движения случайна и по величине и по направлению. При подходе молекулы к стенке происходит удар: молекула деформирует стенку (сминает), далее стенка упруго локально отталкивает молекулу обратно, и весь этот процесс происходит за какое-то время Δτ секунд. Если до удара нормальную к стенке компоненту вектора скорости поступательного движения молекулы обозначить как W, то после удара ее скорость станет равной –W (минус). Это означает, что количество движения молекулы изменилось на величину -2 μW. (μ – масса молекулы). Но согласно второму закону Ньютона это означает, что на молекулу действовала сила F в течение времени Δτ:
-2μW = F Δτ. Следовательно, каждая молекула, ударившись о стенку, оказывает на нее силовое воздействие F. И это воздействие случайно. Найдем среднее значение силы ударов молекул по стенке, усредняя по множеству этих молекул за время много большее Δτ, разделим на величину площади поверхности стенки и получим величину давления р.
Опять обращаем внимание, что чем больше будет ударов молекул р стенку, тем точнее, ближе к истине величина р. Что такое давление, если у стенки «бегает» одна молекула, не знает никто.
Забегая вперед, заметим, что, чем больше молекул находится у стенки (чем больше плотность газа ρ), тем естественно больше давление р. Одновременно, чем больше скорость W молекул (т.е. чем больше температура газа), тем тоже больше давление р. А от этих рассуждений уже и не далеко до вывода уравнения состояния идеального газа.
Температура Т, К.
Рассмотрим поступательное движение молекул вещества, их колебательное и вращательное движения. Каждому из них можно сопоставить количество кинетической энергии. Так как поведение молекул реального газа стохастично, случайно, то и количество кинетической энергии молекул вещества тоже случайно. Можно найти среднее значение этих энергий по множеству всех молекул и сопоставить это среднее значение с температурой. В частности, в статистической физике показывается, что при рассмотрении простейшего газа, молекулы которого представимы в виде материальных точек (нет вращения и колебаний) получается следующее. Оказывается, что среднее значение (математическое ожидание) кинетической энергии поступательного движения молекулы равно 3/2 kT, где k – константа Больцмана. Следовательно, термический потенциал в термодинамике Т можно понимать именно как среднюю кинетическую энергию поступательного движения молекул вещества.
И опять-таки никто не знает, что такое температура одной, двух молекул. Оценка среднего значения по одной двум молекулам такая «плохая», что ее нельзя считать физической величиной.
В теории плазмы физики вынуждены вводить в рассмотрение аж две температуры. Одна – для атомов без электронов, другая – для электронов: уж очень большая разница в скоростях и массах.
Если вещество находится в газовой фазе, то температура характеризует преимущественно кинетическую энергию поступательного движения молекул. Для жидкой и твердой фазы поступательное движение сильно затруднено из-за большой плотности. Для твердой фазы характерно колебательное движение атомов и молекул, для жидкой еще и вращение. Энтропия s. дж/кг К.
Рассматривая интерпретацию термодинамических параметров состояния с точки зрения статистической физики, можно увидеть, что эти параметры являются математическими ожиданиями некоторых случайных величин:
Мх = ∫а х f(x) dx
где Мх – среднее значение случайной величины х, f(x) – плотность распределения ве-
роятностей этой случайной величины. В теории вероятностей все просто: f(x) - известна, значит надо взять интеграл и получить величину математического ожидания. Больцман поставил вопрос совсем иначе: сколько существует распределений молекул (т.е. функций f(…)) в пространстве координат и скоростей, чтобы получить одну и туже величину средних величин? Математик, не задумываясь, ответит – бесконечно много. Физик с ним согласится, что действительно много. Чтобы не работать с огромными числами, Больцман предложил работать с их логарифмами. Если общее число вариантов распределений молекул в пространстве координат и скоростей обозначить как W, то по Больцману s = k lnW
где k - константа Больцмана, s- энтропия.
Иллюстрацией может служить толпа людей, митингующих на площади, затем те же люди, идущие на демонстрации, наконец, те же люди как в армии построенные в колонну и марширующие по той же площади. Здесь видно, что хаоса, беспорядка все меньше и меньше, поэтому и энтропия все меньше. Зато средние значения каких-то случайных величин по множеству людей одни и те же.
Подведем итоги: статистическая физика рассматривает термодинамические параметры состояния как средние значения некоторых случайных величин, усредненных по огромному множеству молекул в геометрическом и скоростном пространстве. Энтропия – мера хаоса и беспорядка, мера числа разных распределений вероятностей, дающих одни и те же средние значения некоторых случайных величин.
Ранее первый закон термодинамики, будучи специализированной формой записи закона сохранения энергии, был записан в виде:
du = Tds – pdv
Здесь приращение внутренней энергии выражено через параметры состояния рабочего тела: термические T и s и деформационные р и v. Первое слагаемое в (2.1) справа представляет собой количество термического взаимодействия между внешней средой и рабочим телом dq = Tds, т.е. количество теплоты, подведенной (отведенной) к рабочему телу. Второе – количество деформационного взаимодействия между внешней средой и системой, т.е. работу сжатия (расширения) dw = pdv. Поэтому иногда удобно записывать первый закон термодинамики в виде:
du = dq – dw
где слева характеристика энергии системы, а справа – количества воздействий внеш-
ней среды на систему.
В основном уравнении термодинамики du = dq – dw фигурируют три величины. Чтобы это уравнение стало расчетным инструментом термодинамики, необходимо дать правила независимого расчета по крайней мере двух величин из трех, входящих в du = dq – dw. Начнем с анализа функции u(s,v).
Внутренняя энергия.
Рассмотрим интеграл по замкнутому контуру (циклу) от основного уравнения du = dq – dw
du dq dw
и обратимся к рисунку (2.5)
Рис. 2.5. Иллюстрация к пояснению полноты дифференциала du
Пусть процесс начинается в состоянии (точке) 1, доходит до состояния (точки) 2 и завершается снова в точке 1. Из определения понятия уравнения состояния следует, что
T = T(s,v) и p = p(s,v)
Эти же аргументы относятся к функции u = u(s,v), т.е. u(∙) зависит только от координат (параметров) состояния s и v термодинамической системы, и это естественно с физической точки зрения – ее возврат в исходное состояние (точка 1), где внутренняя энергия имеет только одно определенное значение. Следовательно, для замкнутых (круговых) процессов
– в термодинамике они названы циклами:
du0
Поэтому из математического анализа (из теории функций многих переменных) следует, что du – полный дифференциал и изменение функции Δu в любом процессе 1 - 2
2
u2 –u1 =u du
1
или в графической форме - при переходе от точки 1 к точке 2 - не зависит от траектории процесса перехода из точки в точку (см. рис 2.2), а в действительных явлениях характер процесса не влияет на изменение внутренней энергии – оно определяется только состоянием (параметрами) в начале и конце процесса.
Рис. 2.6. Изменение внутренней энергии u(s,v) не зависит от траектории F(s,v) = 0 перехода из точки 1 в точку 2
Определение: Величины (функции), изменение которых не зависят от характера процесса, а определяются только состояниями (параметрами) начала и конца процесса, называются функциями состояния.
Энтальпия.
Вновь вернемся к первому закону термодинамики, записанного через параметры состояния du = Tds – pdv. Справа и слева в уравнении прибавим полный дифференциал d(pv) и проведем простые преобразования:
du + d(pv) = Tds – pdv + d(pv) → d(u + pv) = Tds + vdp → dh = Tds + vdp
Эта цепочка равенств – справедлива, т.к. сумма полных дифференциалов равна дифференциалу суммы функций, а d(pv) = pdv + vdp по правилу дифференцирования произведения функций. В du + d(pv) = Tds – pdv + d(pv) → d(u + pv) = Tds + vdp → dh = Tds + vdp мы приняли, что
h ≡ u + pv, Дж/кг или Дж/кмоль
Это тождество по существу является определением новой функции h(s,v), которая по построению является функцией состояния и стандартизованно ее называют энтальпией (ранее в термодинамике называлась теплосодержанием).
Свободная энергия и свободная энтальпия.
Проделаем процедуру перестановки переменных – термических параметров еще два раза:
du – d(Ts) = Tds – pdv – d(Ts) → d(u – Ts) = -sdT – pdv → df = -sdT – pdv. Дж/кг
dh – d(Ts) = Tds + vdp – d(Ts) → d(h –Ts) = -sdT + vdp → dg = -sdT + vdp. Дж/кг
Здесь, как и раньше, от обеих частей уравнений du = Tds – pdv и du + d(pv) = Tds – pdv + d(pv) → d(u + pv) = Tds + vdp → dh = Tds + vdp вычли одну и туже величину d(Ts), снова воспользовались свойствами дифференциалов и дифференциалом произведения функций.
Функция f(s,v) ≡ u - Ts (ее в термодинамике называют свободной энергией или по стандарту – функцией Гельмгольца) является функцией состояния, а df – является полным дифференциалом. Функция g(s,v) ≡ h – Ts ≡ u + pv – Ts (ее в термодинамике называют свободной энтальпией или по стандарту – функцией Гиббса[14]) также является функцией состояния, а ее дифференциал dg – полный.
Эти термодинамические характеристические функции (или термодинамические потенциалы) широко используются при анализе химических и фазовых превращений, при определении направления этих превращений и их полноты. Численные значения Δu и Δh можно получить, зная свойства рабочего тела (вещества) или аналитические связи канонически сопряженных параметров T – s и p – v.
Не будет преувеличением назвать эти четыре характеристические функции фундаментальными, т.к. в совокупности их можно отнести к так называемому «первому закону термодинамики» полностью качественно (по видам взаимодействия) и количественно (по возможности через них расчета процессов: параметров состояния, изменения энергии рабочих тел, количеств внешних воздействий). Так как общее число внешних воздействий равно двум, то количество характеристических функций равно ровно четырем. Сведем эти результаты в таблицу для пущей наглядности.
|
Функция состояния Дж/кг |
Полный дифференциал через параметры состоя- ния |
Наименование функции |
|
u |
du=Tds-pdv |
Внутренняя энергия |
|
u+pv=h |
dh=Tds+vdp |
Энтальпия |
|
u-Ts=f |
df=-sdT-pdv |
Свободная энергия (функция Гельмгольца) |
|
u+pv-Ts=g |
dg=-sdT+vdp |
Свободная энтальпия (функция Гиббса) |
Таб. 2.1. Термодинамические характеристики функций
При выводе функций состояния h, f и g центральную роль играет внутренняя энергия u(s,v), первый закон термодинамики и полнота дифференциала du. В инженерно-технических расчетах чаще всего используется внутренняя энергия u и энтальпия h. Их изменение в процессах (Δu и Δh) равно количеству соответствующего внешнего воздействия. Так, при s = const величина Δu равна работе w адиабатического процесса, при v = const величина Δu равна количеству теплоты q. При p = const количество теплоты q равно величине Δh. Таким образом, через приращения функций состояния вычисляются количества внешних воздействий (функций процесса).
Каждое из четырех дифференциальных выражений может служить для вывода связи параметров состояния. Эти связи в термодинамике называются «Уравнениями Максвелла» или дифференциальными соотношениями. Действительно, если u = u(s,v), то
du = (∂u/∂s)vds + (∂u/∂v)sdv и du = Tds – pdv
Отсюда: T = (∂u/∂s)v и -p = (∂u/∂v)s
В математическом анализе существует теорема о равенстве вторых смешанных производных. Тогда
∂2u/∂s∂v = ∂2u/∂v∂s → (∂T/∂v)s = -(∂p/∂s)v
Это уравнение связи четырех термодинамических параметров в технике или в природе и характеризует количественно равенство двух совершенно разных физических эффектов: изменение температуры Т при изменении удельного объема v в адиабатно-изоэнтропийном процессе численно такое же, как изменение давления p при изменении энтропии s (т.е. при равновесном теплообмене) в изохорном процессе. Получить такую взаимосвязь иным, т. е. не термодинамическим, способом в принципе невозможно.
Предлагаем студентам для тренировки самостоятельно вывести еще 3 дифференциальных соотношения из выражений для dh, df, dg.
По существу, единственная содержательная суть термодинамики – это первый закон термодинамики + диффсоотношения! А где она применяется (техника, химия, электромагнитные процессы, коммерческие фирмы, коммерческие банки и т.д.) – дело прикладников термодинамики.
Если справедливо du 0, то для замкнутого контура
процессов (цикла)
dq dw 0 , dqdw
т.е. сумма внешних теплот за цикл равна сумме внешних работ, а это может быть не только при нулевых слагаемых справа. Рассмотрим рис.2.3 и прейдем к процессам 1 – а – 2 и 2 – в – 1:
Рис. 2.7. Иллюстрация неполноты дифференциалов dq и dw
2 1 2 2 2 2
![]() dq
dqa dqb dqa dqb Tdsa Tdsb ;
dq
dqa dqb dqa dqb Tdsa Tdsb ;
1 2 1 1 1 1
2 1 2 2 2 2
![]() dw
dwa dwb dwa dwb pdva pdvb
dw
dwa dwb dwa dwb pdva pdvb
1 2 1 1 1 1
Здесь просто интеграл по замкнутому контуру разбили на два обычных интеграла: сначала интегрируем от точки 1 к точке 2 по траектории «а», потом обратно от точки 2 к точке 1 по траектории «в». И провели изменение направления интегрирования во втором интеграле. Из математического анализа известно, что геометрический смысл определенного интеграла от любой интегрируемой функции – это площадь под графиком этой функции. Обращаясь снова к рис. 2.7, видно, что интеграл по замкнутому контуру от количеств внешних воздействий dq и dw равен площади замкнутого контура (цикла) в соответствующих координатах. Наверное, понятно, что эта площадь сильно зависит не только от координат точки 1 и точки 2, но и от вида (формы) самих траекторий перехода из т. 1 в т.2 и обратно. Особенно это наглядно видно на рис.2.8.
Рис. 2.8. Иллюстрация зависимости количества теплоты q и работы w от траектории пути процесса перехода из состояния т.1 в состояние т. 2.
Разная штриховка соответствует разным траекториям (процессам).
Из рассмотренного следует, что интеграл ∫dw (сумма элементарных количеств работы) и, аналогично, ∫dq (сумма элементарных количеств теплоты) зависят от вида траектории при неизменных начальных и конечных состояниях процесса.
Определение: Величины (функции), изменение которых зависят не только от состояния (параметров) начала и конца процесса, но и еще от траектории, называются функциями процесса.
Внутренняя энергия u = u(s,v) является функцией состояния, а теплота q и работа w являются функциями процесса (как, впрочем, и любое другое внешнее воздействие – электрическое, химическое, массообменное и т.д.).
.
Потребность в расчетах количества теплоты в научной и инженерной практике появилась задолго до «рождения» термодинамики. Эта потребность стимулировала появление специальной науки – калориметрии, в которой центральным понятием является понятие теплоемкости. Исторически термин «емкость теплоты» перешел в «теплоемкость», которая различается по многим характеристикам.
Определение: Истинной теплоемкостью вещества называется отношение бесконечно малого количества теплоты к бесконечно малому изменению температуры:
dQ
C ![]() Дж/К dT
Дж/К dT
Смысл слова «истинная» состоит в том, что бесконечно малое приращение температуры dT берется от какой-то температуры Т. Поэтому истинная теплоемкость является функцией от самой температуры (параметр, влияющий на свойства вещества).
Наверное, понятно, что при одном и том же изменении температуры dT элементарное количество теплоты dQ и, следовательно, теплоемкость при таком изменении зависят от количественной меры вещества. В химической технологии – это число молей (кмоль), в технике и быту количество вещества определяют или массой m (кг), или объемом V0 при нормальных условиях (нм3)(в химии р0 = 760 мм. рт. ст, Т0 = 298К). Поэтому истинную теплоемкость относят (уделяют) на одну из этих мер. Соответственно, получается удельная истинная теплоемкость массовая, мольная и объемная. Их обозначения (не стандартизованы) и размерность следующие: [c] = Дж/кгК, [μc] = Дж/кмольК, [c΄] = Дж/нм3К.
Определение: Средней теплоемкостью называется
t t2 q 1 2
![]() cm t1 T
t 2 t1
t1 cdT , ΔT = t2 – t1
(2.10)
cm t1 T
t 2 t1
t1 cdT , ΔT = t2 – t1
(2.10)
Индекс «m» внизу у значка теплоемкости присвоен для обозначения слова «средний» (от английского слова middle или немецкого mittel). По существу, средняя теплоемкость – это средне интегральная величина истинной теплоемкости.
Иными словами, средняя теплоемкость вещества в каком-то интервале температуры – это количество теплоты, которое надо подвести (отвести) к (от) рабочему телу, чтобы изменить его температуру на 1 градус.
Так как удельное (полное) количество теплоты q (Q) является функцией процесса, то в калориметрии пришлось отдельно рассматривать теплоемкости по процессам: изохорную (v = const) и изобарную (p = const), так как эти процессы наиболее часто применяются на практике (емкости, трубы, аппараты и т.д.) Обозначение этих теплоемкостей (калорических
![]() t2t2 величин) следующее: ср,
сv или cp t1 , c v
t2t2 величин) следующее: ср,
сv или cp t1 , c v ![]() t1 для истинных и средних
теплоемкостей соответственно.
t1 для истинных и средних
теплоемкостей соответственно.
В итоге выстраивается обширная классификация теплоемкостей: по интервалам температур на истинные и средние, по количествам вещества на массовые, мольные и объемные; по свойствам самих веществ; и, наконец, по множеству видов процессов, среди которых чаще всего встречаются изохорный и изобарный. Это численное и содержательное обилие теплоемкостей требует внимательного отношения к символам и размерностям рассмотренной калорической величины. Мы рекомендуем студентам в своей учебной работе всякий раз четко понимать и обозначать, о какой же теплоемкости в их расчетах идет речь (а их оказалось 7 видов без учета свойств веществ, а с ними и номенклатуры теплоемкостей). При любых расчетах всегда надо указывать размерность и номенклатуру (т.е. название) используемой теплоемкости. Тогда удельное количество теплоты находится как:
q
= c m ![]() tt12 ΔT, Дж/кг, q = μcm
tt12 ΔT, Дж/кг, q = μcm ![]() tt12 ΔT, Дж/кмоль, и q = cm'
tt12 ΔT, Дж/кмоль, и q = cm' ![]() tt12 ΔT, Дж/нм3.
tt12 ΔT, Дж/нм3.
А полное количество теплоты находится как:
Q
= mq = mcm ![]() tt12 ΔT, Q = nq = n μcm
tt12 ΔT, Q = nq = n μcm ![]() tt12 ΔT, Q = V0q = V0 cm'
tt12 ΔT, Q = V0q = V0 cm' ![]() tt12 ΔT, Дж.
tt12 ΔT, Дж.
Соотношение теплоемкостей, отнесенных к разным количествам вещества следующее:
μс = μ∙с = с΄∙22,4 кДж/кмольК
. Существуют многочисленные табличные данные в справочной литературе по этим величинам теплоемкостей. Но для прикидочных расчетов, в которых нет особых требований к точности результата, полезно пользоваться постоянными величинами теплоемкостей, которые приводятся в таблице ниже.
|
Газ |
μcv, кДж/кмоль К |
|
Одноатомный |
12,6 |
|
Двухатомный |
20,9 |
|
Трех и более атомный |
29,1 |
|
|
|
Таб. 2.2. Приближенные значения мольных теплоемкостей газов при невысоких температурах
Окончательно: теплоемкость, как калорическая (тепловая) величина, не относится к категории функций состояния и тем более к параметрам состояния. Строго говоря, понятие теплоемкости чуждо термодинамике, так как количество термического воздействия внешней среды на систему можно рассчитать и без теплоемкости как dq = Tds. Тем не менее обилие справочного материала по теплоемкости для большого числа веществ и привычка к этой калорической характеристике сделали ее широко употребительной в термодинамических и других физико-химических расчетах.
Теперь с помощью простых физических соображений покажем, что изобарная теплоемкость любого вещества всегда больше изохорной (ср > cv).
Сначала проведем мысленный эксперимент, как бы используя экспериментальную установку на рис.2.5.
Рис.2.9. Схема двух экспериментов.
Измеряемые величины: температура Т с помощью термопар, давление р с помощью манометра, количество теплоты q
В первом случае (слева) просто нагреваем баллон с газом, во втором – нагреваем и поддерживаем постоянное давление в сосуде, позволяя газу расширяться. Зададимся вопросом: «В каком случае необходимо подвести больше теплоты, если начальная температура Т и ее изменение ΔТ в обоих случаях одинаковы?». Или иначе: «Какая теплоемкость больше: ср или сv?».
Ответ основывается на принципиальном различии экспериментов: слева термодинамическая система деформационно изолирована от внешней среды, т.е. не может совершить работу dw = pdv, а справа – может. И газ по-прежнему нагревается на ΔТ от подведенной теплоты qv = cvΔT, а во втором случае qp = qv(ΔT) + q(w) ≡ cpΔT. Поэтому ответ на поставленный вопрос: ср > сv.
Из вышеизложенного материала и анализа определения теплоемкости понятно, что количество теплоты можно определить двояко – через теплоемкости и через энтропию. Действительно, dq = cdT или dq = Tds, т.е. cdT = Tds, а переходя на геометрическую интерпретацию определенного интеграла ∫dq, как площади под кривой, можно воспользоваться тепловыми диаграммами с координатами с – Т или Т – s (см. рис. 2.10.).
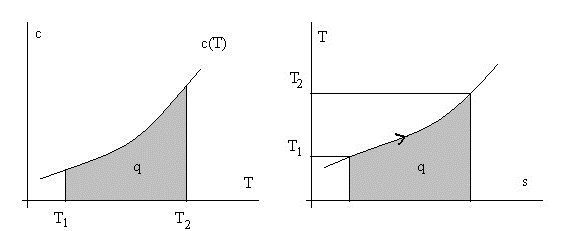
Рис.2.10. Тепловые диаграммы с – Т и Т – s для некоторого вещества. Заштрихована площадь, численно равная количеству теплоты.
Разумеется, вторая, т.е. Т – s диаграмма, более содержательна и строга, т.к. она имеет координаты в виде функций состояния. Остается для интегрирования выразить T через s (или сх через Т), что возможно при известных свойствах веществ.
Второй закон термодинамики по своим формулировкам неоднократно дополнялся за более чем полуторавековое существование науки – термодинамики. Если бегло взглянуть в соответствующий раздел нескольких монографий или даже учебников по технической термодинамике, то без специальной консультации едва ли можно утвердиться в понимании второго закона термодинамики. Лишь совершенно очевидно при первом знакомстве с этим законом, что речь идет о переносе теплоты в циклах и о характере изменения при подобном переносе параметра – энтропии. Это впечатление не случайно, а исторически предопределено самим становлением термодинамики.
Становление термодинамики приняло систематический характер со времени публикации во Франции в 1824 году первой и единственно прижизненной научной статьи инженера-артиллериста по образованию и молодого ученого Саади Карно. В статье впервые в науке было введено понятие «движущая сила» применительно к теплопереносу – ΔТ – конечной разности температур, которая всегда создает неравновесный (необратимый) процесс.
В 1851 году немецкий профессор Рудольф Клаузиус[15] ввел в научный оборот новую для термодинамики функцию – энтропию через рассмотрение переноса теплоты в обратимых (терморавновесных) циклах. Р. Клаузиус показал, что в круговом процессе
∫dQ/T = 0,
и тем самым доказал существование функции состояния S и полноту ее дифференциала:
dS = dQ/T.
Далее, им показано на инженерном примере необратимого (термонеравновесного) теплосилового цикла возрастание этой функции (параметра) S при переносе теплоты с высшего температурного уровня на низший в условиях необратимости. Например, при наличии конечных разностей температур между рабочим телом и верхним (по температуре) источником теплоты. Однако, автор столь фундаментального вывода, относящегося к пятидесятым годам Х1Х века, основное внимание сосредоточил на главном вопросе теплотехники – эффективного перевода теплоты от верхнего источника (котельного агрегата в современной терминологии) к нижнему (холодильнику или конденсатору) с целью получения работы в реальном необратимом теплосиловом цикле.
Далее, по Л.Н. Толстому: «Все смешалось в доме Облонских.» – стали в единстве рассматривать введение нового параметра состояния – энтропии, ее обязательный рост в природных (т.е. неравновесных) процессах и, наконец, невозможность превращения всей внешней теплоты из внешнего источника полностью во внешнюю работу.
В действительности, введенные Р. Клаузиусом три новых научных положения должны рассматриваться как самостоятельные проблемы:
• есть параметр состояния теплового взаимодействия – энтропия, и она нашла свое место в термодинамике и не только в ней;
• есть закономерность неполного превращения подведенной теплоты в работу в замкнутых процессах (циклах);
• есть явление обязательности роста энтропии в естественных (самопроизвольных) неравновесных (необратимых) системах (совсем необязательно с замкнутыми процессами).
Вторая проблема существенна для узкого круга приложений технической термодинамики – теории тепловых и холодильных установок, но не для науки-термодинамики. Последняя проблема по существу является констатацией эмпирического факта, математическая запись которого имеет вид:
dS = dQ/T + Δ, Δ > 0
для необратимых процессов. И этот факт ученые-термодинамики оставили у себя в
термодинамике в качестве второго закона.
Окончательно, приведем лишь одну из множества существующих формулировок второго закона термодинамики, предложенную немецким ученым Максом Планком[16]:
«Всякий происходящий в природе процесс протекает в таком направлении, что сумма энтропий всех участвующих в процессе тел увеличивается».
Самопроизвольный процесс – процесс, происходящий без участия человека. Действительно, поток воды водопада Ниагары имеет на верхнем уровне запас потенциальной энергии, природа создала условия для падения воды, т.е. для превращения потенциальной энергии в кинетическую, Последняя в конце концов превращается в тепловую. Но та же вода на гидростанции вращает водяные турбины и далее электрогенераторы. Здесь человек создал условия превращения потенциальной энергии воды в водохранилище в электроэнергию. Но после создания условий процесс превращения происходит уже без участия человека, т.е. самопроизвольно.
Многочисленные экспериментальные данные, да и просто житейские наблюдения, показывают, что теплота самопроизвольно переходит из области высоких температур в область низких; что материальный поток самопроизвольно течет из области высокого давления в область низкого; что два разных газа самопроизвольно смешиваются (диффундируют), если убрать перегородку между ними; что электрические заряды самопроизвольно движутся из области высокой напряженности электрического поля в область низкой и т.д. и т.п.
Эти примеры показывают, что необходимым условием течения процессов является разность потенциалов: внешнего Рje и внутреннего Рj (j = 1, 2, 3,….n)
ΔРj = Рje – Pj.
Чем больше разность ΔРj, тем больше мера превращения, т.е. изменение сопряженной координаты состояния Δxje (см. лекцию 1 и критерий стабильности термодинамики). Снова отсылая к лекции 1, напомним, что
du = ∑dKj = ∑Pjdxj + ∑ΔPjdxj.
Основной эмпирический факт состоит в том, что при конечной разности потенциалов взаимодействия термодинамической системы и внешней среды получается
∑ΔPjdxj = Tdsдиссип, dsдиссип > 0
Иными словами, результат этого превращения при конечной разности потенциалов взаимодействия любого рода как бы включает «внутреннее» термическое воздействие: часть превращаемой энергии (часть количества воздействия) всех родов рассеивается (диссипирует) и обращается в «теплоту», а значит
dsдиссип = dQдиссип /Т > 0.
В этом и состоит суть и смысл второго закона термодинамики.
Замечание. Человеку в его производственной деятельности по созданию организованной материи, энергии и информации свойственно стремление производить быстро, много и высокого потребительского качества. Чем же приходится платить за скорость процессов и за качество продукции? А платить приходится большими разностями потенциалов взаимодействия и, в конце концов, согласно ∑ΔPjdxj = Tdsдиссип, dsдиссип > 0 ростом энтропии в системе человек + производство + внешняя среда. Для химиков-технологов стремление к большим производительностям установок, к высокой степени выделения целевого продукта из смесей приходится объективно оплачивать большой себестоимостью этого продукта.
Следовательно, быстро – значит дорого, медленно – значит дешево.
Термодинамическая основа этого вывода в том, что высокоупорядоченные виды энергии (электрическая, все виды топлива, водяной пар больших параметров, высокие давления катализа и синтеза и т.д.), будучи очень дорогими, превращаются в тепловую энергию, энергию хаотического, беспорядочного движения с малым термическим потенциалом по отношению к внешней среде, а зачастую с потенциалами самой среды. И такую энергию просто невозможно использовать далее для производства.
1. Если потереть ладони рук друг о друга, то кожные рецепторы почувствуют, как бы приток теплоты: механическая работа трения рассеялась и проявляется как теплота.
2. Камень с массой m падает с высоты H на землю. Изменение энтропии системы камень + земля равно
ΔSдиссип = mgH/T0,
где g = 9,81 м/с2 – ускорение свободного падения, Т0 – температура системы камень +
земля. Если совершить работу mgH Дж и снова поднять камень на туже высоту Н, то система камень + земля отнюдь не возвращается в исходное состояние (камень возвращается, а система – нет), т.к. в системе осталась теплота Т0dSдиссип . Надо совершить работу, затратить энергию, чтобы отвести эту теплоту в надсистему.
3. Самопроизвольный переход теплоты. Рассматриваются два тела А и В с разными температурами ТА и ТВ, помещенные в адиабатические условия. Можно строго показать, что в такой системе начнется самопроизвольное увеличение энтропии:
dS = dSA + dSB > 0.
Переток энергии от горячего тела к холодному прекращается при ТА = ТВ, и тогда dSА + dSB = 0. Но если приращение какой-то величины сначала растет, а потом становится нулевым, то сама величина в конце процесса становится максимальной. Следовательно, в конце процесса, когда ТА → ТВ, SA + SB → max.
4. Самопроизвольное расширение газа. Рассматриваются два объема газа с разными давлениями рА и рВ и затвором между ними. Как только уберем затвор, то начинается процесс течения газа из объема с большим давлением в объем с меньшим. Можно строго показать, что в такой системе происходит необратимое увеличение энтропии
T(dSA + dSB) = (pA – pB)dvA, dvA = -dvB, dSA +dSB > 0.
Течение газа будет происходить до тех пор, пока давления в сосудах не сравняются, тогда наступит равновесие, dSA + dSB = 0. Следовательно, в момент прекращения течения газа SA + SB = max.
5. Самопроизвольное смешение двух разных идеальных газов. Рассмотрим термически изолированный сосуд с перегородкой, разделяющей сосуд на две части А и В. В каждой части разместим разные газы А и В при одинаковом давлении. После ликвидации перегородки молекулы газов А и В начинают диффундировать и заполнять весь объем сосуда VA + VB . Можно строго показать, что энтропия системы после снятия перегородки начнет увеличиваться
dS = dSA + dSB = R(NAlnVA + NBlnVB) > 0.
Здесь NA и NB число киломолей газа А и В соответственно, VA и VB – геометрический объем газов до снятия перегородки.
Процесс смешения газов А и В прекратится, как только каждый газ равномерно заполнит объем всего сосуда. Тогда наступит равновесие
dSA + dSB = 0 и SA + SB = max.
Вопрос. Как изменится энтропия системы, если в каждой части сосуда в начале будет один и тот же газ, например, кислород? Молекулы газа из части А не будут диффундировать в часть В и наоборот?
6. Процесс приготовления пищи на кухне, сам процесс пищеварения в желудке и кишечнике человека – типичный пример необратимого роста энтропии. И все это во имя того, чтобы продукты питания приняли форму и вид, пригодных для усвоения, впитывания кишечником. Этот процесс усвоения происходит под действием разности концентраций (разности потенциалов) питательных веществ внутри кишечника и в крови, омывающей кишечник. Кстати, чтобы полностью усвоить все полезные компоненты в пище, необходим кишечник ∞ длины. Поэтому природе пришлось сделать кишечник конечной длины (12 м у взрослого человека), но платить за это приходится тем, что коэффициент полезного действия органов пищеварения у человека 60%. Остальное приходится выбрасывать. У коровы кпд = 80%, но у нее два желудка и более длинный кишечник.
Вообще, вся деятельность человека, начиная с процессов на клеточном уровне и кончая сознательной работой, направлена на уменьшение энтропии в себе и для себя за счет еще большего роста энтропии в системе человек + окружающая среда. Обломов меньше генерирует энтропию в окружающую среду, чем его товарищ деятельный Штольц.
7. Почему клетки делятся? Смысл одной из гипотез основан на втором законе термодинамики. Рассуждения таковы. Все процессы обмена и превращений в клетке объективно происходят при конечных разностях потенциалов. Следовательно, обязательно происходит генерация энтропии, клетка как бы самонагревается. А отвод теплоты (точнее, энтропии) происходит через поверхность клетки в межклеточную жидкость и далее в венозную кровь. Генерация энтропии происходит в объеме клетки, т.е. ~ d3, а отвод ее происходит через поверхность, т.е. ~ d2. Следовательно, существует такой размер клетки d0, при котором интенсивность генерации энтропии равна интенсивности отвода ее. В начале своего жизненного цикла клетка мала, далее она самопроизвольно растет и по объему и по массе. Если ее размер превзойдет величину d0, то начнется рост температуры и нарушение течения химических реакций синтеза и деструкции белков. Чтобы избежать своей гибели, клетке с неизбежностью придется уменьшить свой размер, т.е. разделиться на две малых клетки.
Вопрос. А почему нервные клетки взрослого человека не делятся, т.е. не размножаются, если верна предложенная гипотеза?
Тема 2.3. Идеальные газы
Внутренняя энергия u(s,v) является функцией координат состояния s и v. С другой стороны имеем уравнение состояния рабочего тела, предоставленное физиками, T = T(s,v). Из этого уравнения ничто не мешает найти энтропию s = s(T,v) и подставить ее в зависимость для u(s,v). Получим новую зависимость u(s(T,v),v) = u(T,v) и для последней распишем полный дифференциал внутренней энергии du:
du = (∂u/∂T)vdT + (∂u/∂v)Tdv
Еще запишем основное уравнение термодинамики в двух формах:
dq = du +dw, или dq = du + pdv, где dq =схdT в произвольном процессе.
Пусть х = v = const, т.е. конкретизируем изохорный процесс (dv = 0), и тогда схdT = cvdT = du, т.е.
сv = (∂u/∂T)v
После подстановки этого выражения в du = (∂u/∂T)vdT + (∂u/∂v)Tdv получаем:
du = cvdT + (∂u/∂v)Tdv
Получили очень важный результат в виде du = cvdT + (∂u/∂v)Tdv – уравнение для расчета изменения внутренней энергии. Если рассмотреть еще энтальпию h(s,v), снова сделать замену переменных h(T,p) с помощью уравнений состояния, далее провести процесс х = p
= const над рабочим телом, то получим уравнение для расчета изменения энтальпии:
dh = cpdT + (∂h/∂p)Tdp
Уравнения du = cvdT + (∂u/∂v)Tdv и dh = cpdT + (∂h/∂p)Tdp справедливы для любых веществ и любых процессов c рабочим телом.
Определение: Идеальным газом называется такое состояние вещества, при котором можно пренебречь силами взаимодействия между молекулами этого вещества.
В этом определении понятия идеального газа подчеркивается, что одно и тоже вещество может быть в любом состоянии, в том числе и в состоянии идеального газа. Например, воздух при обычных условиях (давление и температура – атмосферные) – является идеальным газом. Тот же воздух в жидком состоянии уже не идеальный газ. Пары воды в составе атмосферного воздуха – идеальный газ, а вода в состоянии близком к кипению или конденсации – нет.
В первой лекции было дано определение понятия уравнения состояния: это функциональная зависимость потенциала взаимодействия системы какого-то рода от всех координат состояния. Для термодеформационной системы (а это и есть предмет изучения технической термодинамики) имеем ровно два уравнения состояния:
T = T(s,v) и p = p(s,v)
Конкретный вид этих зависимостей предоставляют физики для каждого индивидуального рабочего тела (вещества). Как показано в лекции 1, можно провести несложную замену переменных:
T = T(s,v) → s = s(T,v) → p(s(T,v),v) = p(T,v).
И получаем другую пару уравнений состояния:
T = T(s,v) и p = p(T,v)
Чисто исторически получилось так, что одно из этих уравнений состояния появилось на свет задолго до появления понятия энтропии и включает в свой состав легко измеряемые в опытах параметры p, v,T, формализуемые в уравнение p = p(T,v)
Вначале уравнение состояния идеального газа было получено экспериментально для условий с небольшими давлениями и температурами. В дальнейшем это уравнение было получено строго на основании молекулярно-кинетической теории газов.
Для 1 кг вещества уравнение состояния идеального газа p = p(T,v) имеет вид:
pv = RуТ
Для произвольного количества вещества:
pV = mRуT
Если в ряду произвольных количеств вещества выбирается молярное количество, то:
pV΄ = nRT
В этих 3х уравнениях p, н/м2, v, м3/кг,T, К – параметры состояния, Rу = 8314/μ Дж/кгК, R = 8314 Дж/кмольК – универсальная газовая постоянная, V – геометрический объем, который занимает вещество, м3, V΄ - его молярный объем нм3/кмоль, m – масса, кг, n – кмоль количество вещества, μ – мольная масса вещества, кг/кмоль.
Условие критерия стабильности (см. первую лекцию), который определяет принцип достоверности построения любого уравнения состояния, выполняется для pv = RуT:
p = RуT/v → (∂(-p)/∂v)T = RуT/v2 ≥ 0.
Еще раз вернемся к основному уравнению термодинамики:
dq = du + pdv → cxdT = cvdT + pdv и
рассмотрим частный случай: рабочее тело находится в состоянии идеального газа и совершается процесс х = p = const. Тогда из предыдущего уравнения следует, что
cp = cv + p(∂v/∂T)p и pv = RуT → v = (R у/p)T → (∂v/∂T)p = Rу/p.
Окончательно, получаем
cp = cv + Rу, и, конечно, cp > cv
Соотношение между теплоемкостями cp = cv + Rу, и, конечно, cp > cv в термодинамике носит название закона Майера[17]. Из него следует, что на практике достаточно определить только одну теплоемкость cp или сv, чтобы сразу найти другую. И не будем забывать, что закон Майера справедлив только для идеального газа. Для реальных веществ с другими уравнениями состояния можно лишь говорить, что cp > cv.
Уравнение Майера справедливо не только для истинных теплоемкостей, но и для средних.
Как ясно из выведенных уравнений du = cvdT + (∂u/∂v)Tdv и dh = cpdT + (∂h/∂p)Tdp внутренняя энергия и энтальпия зависят от свойств веществ. Действительно, первое слагаемое включает теплоемкость в явном виде, а во втором слагаемом она же входит в неявном виде как u = u(cv, T). Одновременно, свойства веществ отражаются уравнениями состояния u = u(s,v) и h = h(s,v). Следовательно, оценку роли u и h и их связи с поведением рабочих тел можно установить только, если известны уравнения состояния конкретного вещества (рабочего тела).
Из определения идеального газа следует, что внутренняя энергия идеального газа является просто кинетической энергией хаотического поступательного движения молекул газа. Потенциальная энергия взаимного расположения молекул в геометрическом пространстве, вращательная и колебательная энергия молекул идеального газа пренебрежимо малы по сравнению с кинетической энергией поступательного движения. Именно это обстоятельство позволило Больцману корректно провести усреднение кинетической энергии по множеству всех молекул и получить знаменитую формулу, известную из курса физики:
u = 3/2 kT
где k – постоянная Больцмана, Т – термодинамическая температура, u – средняя по
множеству всех молекул кинетическая энергия.
Выражение u = 3/2 kT по существу показывает, что внутренняя энергия идеального газа является функцией только температуры и что изменение внутренней энергии Δu определяется только изменением температуры:
(∂u/∂(∙))T = 0
Здесь вместо точки в выражении частной производной можно подставить любой параметр состояния (конечно, кроме Т).
Отсюда сразу следует, что для идеального газа расчет изменения внутренней энергии и энтальпии существенно упрощается, т.к. (∂u/∂v)T = 0 и (∂h/∂p) = 0 и
du = cvdT и dh = cpdT →
Δu =cv ![]() tt12 (t2 – t1); Δh =cp
tt12 (t2 – t1); Δh =cp ![]() tt12 (t2 – t1);
tt12 (t2 – t1);
И такой способ расчета изменений функций состояния справедлив для любых процессов с идеальным газом.
Можно также предложить другой способ расчета изменения функций состояния, если имеется в наличии диаграмма p – v или T – s для какого-то вещества в идеальном состоянии. Например, рассмотрим диаграмму T – s и процесс 1 – 2 на рис. 2.10.
Рис. 2.10. Графический способ расчета изменения внутренней энергии и энтальпии для идеального газа в процессе 1 – 2.
Точки 1 и 2 характеризуют два состояния с температурами Т1 и Т2 (на рис 2.10 показаны две соответствующие изотермы). Изменение энтальпии Δh определяется):
2 2
h dh Tds vdp,
1 1
и для функций состояния Δh не зависит от траектории процесса, а зависит только от температуры в начальном и конечном состоянии (изотермы Т1 и Т2). Из уравнения видно, что по диаграмме T – s нельзя найти определенный интеграл от vdp. Тогда расчет Δh будем вести не по реальной кривой, а по изобаре p = const (dp = 0 и vdp = 0) и второй интеграл станет нулевым.
Строим изобару p = const на диаграмме, тогда площадь под изобарой в нужном температурном интервале Т1 и Т2 и будет численно равна изменению энтальпии Δh.
Аналогично,
2 2
u du Tds pdv
1 1
Строим изохору v = const, и площадь под ней в тех же температурных пределах будет численно равна изменению внутренней энергии в процессе 1 – 2.
Замечание. Расположение изохоры или изобары на плоскости с координатами T – s правее или левее относительно процесса 1 – 2 здесь не существенно: площадь под кривыми неизменна.
Также просто найти изменение функций состояния в любом процессе с идеальным газом, если он изображен на диаграмме с координатами p – v. Предлагаем студентам самим проделать эту процедуру в качестве тренировки.
Замечание. Такая простота и легкость расчета изменения функций состояния в любом процессе обусловлена двумя обстоятельствами:
1. Зависимостью внутренней энергии идеального газа только от температуры.
2. Независимостью приращения функций состояния от траектории процесса, а, следовательно, возможностью выбора удобной для интегрирования траектории в интервале лишь температур начала и конца процесса.
«Работа – это изменение формы энергии, рассматриваемая с количественной стороны» - согласно формулировке Энгельса, данной еще в Х1Х веке. Для термодинамики это определение имеет двойное содержание: во-первых, нас будет интересовать количество работы или адекватная ей разность энергий рабочего тела, а, во-вторых, работа всегда связана с «движением», т.е. с упорядоченным перемещением вещества рабочего тела, которое взаимодействует с окружающей его средой.
Для теории, т.е. в нашем случае для термодинамики, существенна скорость взаимодействия, а она в математической терминологии предполагается бесконечно малой; также изменяются и параметры состояния. Подобные процессы («изменения состояния») уже названы (см. лекцию 1) равновесными или квазистатическими (мнимостатическими). В них в каждое мгновение перемены состояния существует равновесие между движущими силами (потенциалами) рабочего тела и окружающей среды и поэтому мы записываем dT, dp, du и т.д.
Естественно, что в подавляющем числе случаев превращения веществ, происходящих в природе и в промышленной практике, не равновесны, и поэтому необратимы в термодинамическом смысле, т.е. нельзя вернуть рабочее тело в первоначальное состояние без дополнительной затраты энергии от окружающей среды (т.е. без компенсации). Поэтому аппарат термодинамики (термостатики) в полной мере и в строгой форме к анализу действительных процессов не применим. Все же анализ подобного рода часто дает примерно верное отражение действительных изменений. Когда же глубина необратимости невелика, действительные изменения отражаются в равновесных (квазистатических) процессах достаточно точно
Задача расчета работы встречалась еще в школьном курсе физики, например, при расчете работы растяжения пружины или при движении груза по плоскости с трением. Для линейного перемещения работа W рассчитывается как
2
W Fdl,
1
где F – сила растяжения пружины, l – перемещение свободного конца пружины. Для объемной деформации (раздувание резинового шара и промышленного газгольдера или сжатие газа в компрессоре) работа равна
2
W pdV ,
1
где р – давление, V – объем газа. Даже эти два примера наводят на важную практическую мысль – количество работы прямо связано с возможностью расширения (сжатия) рабочего тела и с энергетическими резервами окружающей среды (величины движущей силы или возможности ее использования в этой среде).
В практике химических производств (а «химия – это трубы») наиболее часто применяются легко деформирующиеся рабочие тела. Сжатие и расширение газов, их нагревание и охлаждение, испарение жидкостей и конденсация паров, разделение смеси газов и многие другие превращения постоянно встречаются в инженерной практике. Особенно широко используются эти процессы в химической и нефтехимической промышленности, в энергетике. Любые технологические изменения жидкостей, паров и газов основаны на непрерывной смене состояний без возвращения к первоначальному, т.е. относятся к разряду разомкнутых процессов.
Последнее десятилетие вернуло в химии интерес к энергетике из-за резкого повышения стоимости энергоресурсов и мизерного, практически, использования вторичных энергоресурсов в собственно химических производствах. В связи с этим повысился интерес к термодинамике, как к теоретической основе преобразования энергии.
Конечной целью термодинамического расчета процесса является определение параметров состояния, изменения внутренней энергии и вычисление количеств теплоты и работы. Расчет количества работы необходим для определения и экономичного решения задачи подбора приводов дутьевых средств (машин – компрессоров, газодувок, дымососов и вентиляторов для транспортировки газов, и паров).
В терминологии работа внешней среды над рабочим телом – это просто количество деформационного воздействия dw = pdv. Причем, ранее показано, что dw не является полным дифференциалом и что величина
2 2
w dw pdv
1 1
сильно зависит не только от параметров начального и конечного состояния в точках 1 и 2 процесса, но и от его траектории.
Если известно уравнение связи p = p(v), то расчет количества работы сводится ко взятию указанного интеграла. В технической термодинамике эта связь давления и удельного объема чаще всего представляется в виде:
pvn = const или pvn = p1v1n, т.е. p = p1v1nv-n, при n = const
Это уравнение в технической термодинамике носит название политропы – каждое значение n определяет свою «тропу», т.е. траекторию, и отражает связи параметров p и v.
2 2
Если подставить эту зависимость p = p(v) в w dw pdv , то получим таблич-
1 1
ный интеграл, который после несложных преобразований с помощью pvn = const или pvn = p1v1n, т.е. p = p1v1nv-n приводится к одному из следующих видов:
n1
![]() w
pn1 v11 1
pp12
n , Джкг
или w
w
pn1 v11 1
pp12
n , Джкг
или w ![]() n11p1 v1 p2 v2 ,
n11p1 v1 p2 v2 , ![]() Джкг
Джкг
Данные расчетные формулы пригодны для политропического процесса для любого реального вещества.
Для идеального газа с учетом связи pv = RуT расчетная формула в несколько упрощается:
w ![]() T1 T2,
T1 T2,![]() n 1 кг
n 1 кг
Полная работа деформации (сжатия или расширения) за процесс рассчитывается как:
W = mw, Дж, где m – масса рабочего тела.
Если зависимость p = р(v) представлена в графическом виде, т.е. процесс с рабочим телом изображен на диаграмме p – v для какого-то вещества, то расчет количества работы можно провести в соответствии с рис. 2.4, как площадь под линией процесса до оси v.
Расчет количества работы возможен с помощью первого закона термодинамики:
Δu = q – w → w = q – Δu
если предварительно найти изменение внутренней энергии Δu и количество теплоты q так, как показано в этой лекции выше.
Замечание. В этом разделе до сих пор шла речь о работе деформации рабочего тела, т.е. сжатия или расширения термодинамической системы в геометрическом пространстве. Однако, в технической термодинамике необходимо уметь рассчитывать работу проталкивания:
dw΄ = vdp, Дж/кг
Особенно, этот расчет необходим для проектирования компрессоров и для определения мощности их привода. В этом случае dw΄ = vdp называют располагаемой работой.
На рис. 2.11 представлены две диаграммы в осях p – V теоретическая рабочая и p – v термодинамическая для процесса компремирования. Для идеального одноступенчатого компрессора этот процесс состоит из двух изобар и одной политропы с заданным показателем n.
Рис. 2.11. Иллюстрация работы компрессора в диаграммах p – V и p – v.
Процесс 0 – 1 – всасывание исходной газовой среды, процесс 1 – 2 – сжатие, 2 – 3 – проталкивание сжатого газа потребителю.
Площадь слева от кривого процесса сжатия pvn = const и представляет собой затраченную на сжатие газа работу (располагаемая работа):
W'
Vdp . Дж.
Можно перейти к удельному объему v от геометрического V, если уделить последний на все количество газа m, вошедшего в цилиндр компрессора за весь процесс всасывания 0 – 1. Тогда техническая работа компрессора равна
p2
w ' vdp Дж/кг
p1
Снова воспользуемся уравнением политропы:
pvn = const → pvn = p1v1n → v = v1p11/n p-1/n
Иными словами, работа, затраченная на компрессию газа (располагаемая) в n раз больше работы простого сжатия.
Мощность двигателя для привода одноступенчатого идеального компрессора рассчитывается как:
Nдвиг = Gw΄/η, Вт
где G – массовый расход сжимаемого газа, кг/с, η – коэффициент полезного действия
привода.
Замечание. В инженерной практике и, следовательно, в технической термодинамике приходится рассматривать процесс проталкивания газов через каналы, сопла (реактивные двигатели, газовые и паровые турбины). Линейные скорости течения газов в таких каналах настолько велики (звуковые и сверхзвуковые скорости), что процесс течения газа можно рассматривать как адиабатический (нет теплообмена). Это означает, что без учета трения потока газа о стенки канала и трения в самом потоке – s = const, ds = 0. В этой ситуации работа проталкивания рассчитывается через функцию состояния – энтальпию du + d(pv) = Tds – pdv + d(pv) → d(u + pv) = Tds + vdp → dh = Tds + vdp:
2
dh = Tds + vdp → dh = vdp → w΄ = dh = Δh = h2 – h1.
1
2 2
Здесь для идеального газа справедливо выражение h dh Tds vdp, а для ре-
1 1
ального рабочего тела используются расчетные таблицы свойств веществ.
1. p – v диаграмма
На рис. 2.12 представлены графики зависимости pv=RуT для различных изопроцессов: показан ход изобары (p = const), изохоры (v = const), изотермы (pv = const), изоэнтропы (pvk = const) для идеального газа. По построению в p – v координатах две линии – прямые (p и v), одна (T = const) – равнобокая гипербола и неравнобокая – изоэнтропа (s = const) pvk = const.
Такой график удобен для качественного анализа изменения параметров и функций процессов. Для точных расчетов не используется.
Рис. 2.12. Графики зависимостей р от v для различных изопроцессов p, v, T, s = const с
рабочим телом в состоянии идеального газа.
2. T – s диаграмма
Рассмотрим ход кривых p = const и v = const в диаграмме с координатами T – s. В термодинамике количество термического воздействия (теплоты) рассчитывается как dq = Tds, а в калориметрии – как dq = cdT. Отсюда
2
Tds = cdT → ds = cdT/T → s2 –s1
=
[cx(T)/T] dT = cm ![]() tt12
ln T2/T1.
tt12
ln T2/T1.
1
Расчетную формулу для приращения энтропии Δs получим из сх|t2t1 при х = р или х =v:
t2t2
Δs = cp ![]() t1 lnT2/T1 для p =
const и Δs = cv
t1 lnT2/T1 для p =
const и Δs = cv ![]() t1 lnT2/T1
для v = const. (2.31)
t1 lnT2/T1
для v = const. (2.31)
Окончательно,
t2t2
T2 = T1exp{(s –s0)/cp ![]() t1 } и T2 = T1exp{(s –s0)/cv
t1 } и T2 = T1exp{(s –s0)/cv ![]() t1 }.
t1 }.
Таким образом, изобара и изохора в осях T – s являются обычными экспонентами, причем из-за того, что ср > cv, изохора круче изобары (см. рис. 2.13), т.к. dT/ds = T/c – тангенс угла касательной к графику соответствующей кривой.
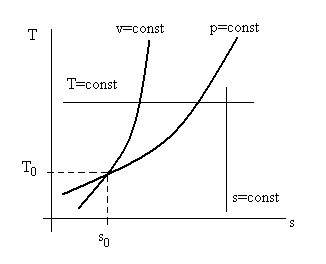
Рис. 2.13. Взаимное расположение графиков процессов
p = const и v = const в осях (Ts), так как cp > cv то изохора проходит круче изобары.
Здесь же показаны процессы s = const и Т = const
В поле графика T – s (см. рис. 2.13) прямые линии T = const и s = const при избранных масштабах температур и условных значений энтропии (отсчет от s0 = 0 в избранном масштабе), а так же экспоненты p = conct и v = const образуют сетку энтропийной (тепловой) диаграммы.
Возможно использование оси ординат для нанесения условного значения энтальпии от h0 = 0: h = cр|t0*t кДж/кг. Такая диаграмма удобна для широко распространенных изобарных и изоэнтропийных процессов. В первом случае (p = const) dh = Tds + vdp, т.е. h = ∫Tds = qp. Во втором (s = const) dh = Tds + vdp, т.е. h = ∫vdp – работа компрессора.
Для инженерной практики теплофизические институты создают диаграммы p – v и T – s для различных веществ и рабочих тел. Использование их существенно ускоряет расчетный процесс, если не требуется особенная точность.
Определение. Процессом называется непрерывная смена состояний рабочего тела.
Термодинамический расчет подобного физического изменения состояний является в сущности приложением выработанного в предыдущих лекциях термодинамического аппарата к инженерным и научно-техническим задачам. Физика обработки технологических потоков в химических технологиях при их различных фазовых состояниях безусловно влияет на методику расчета.
Часто в инженерии используется термин «газ» и нередко термин «пар». Каково происхождение этих терминов и их соотношение? Исторически (в средние века) вещество называли газом, если не могли (по техническим причинам или по неведению) получить его в жидком состоянии. А если могли, то называли паром. Поэтому в те времена воздух называли газом, а Н2О в газообразном состоянии – паром. Сейчас проблема ожижения любого газа (и вещества), даже перевод его в твердое состояние, решена.
Целью расчета процесса является определение исходных данных для создания технологии или расчета, оптимизации и выбора аппарата или машины.
1. До численного решения установить термодинамические особенности процесса (постоянство какого-то параметра или отсутствие какого-то взаимодействия с внешней средой). Иными словами, определить инварианты процесса.
2. Найти уравнение процесса.
3. Получить связь между параметрами состояния (p, v, T,s) рабочего тела для двух произвольных состояний процесса.
4. Рассчитать изменение функций состояния Δu, Δh и изменение энтропии Δs, рассчитать количества внешних воздействий (функций процесса q, w).
5. Изобразить процесс в термодинамической системе координат p – v, T – s, h – s.
Политропный процесс. Уравнение процесса.
Уравнение политропического процесса имеет вид:
pvn = const, n = const
Но это не единственная форма связи параметров состояния, возможны комбинации:
pTn΄ = const, n΄ = const или vTn΄΄= const, n΄΄= const
Далее, для примера, будем работать с уравнением pvn = const, n = const
На практике показатель политропы n находят экспериментально следующим образом:
pvn = const → lnp + nlnv = const → lnp = - nlnv + const
Последнее выражение представляет собой уравнение прямой линии в координатах lnp – lnv. В эксперименте с каким-то веществом для различных условий измеряют давление р и удельный объем v с какой-то инструментальной точностью. Далее строят график в осях lnp – lnv (см. рис. 2.14.) и по нему находят показатель политропы n.

Рис. 2.14. Иллюстрация к экспериментальному определению показателя политропы n – индикаторная диаграмма в логарифмических координатах. n = - tgα.
- обозначение экспериментальных точек.
Истоки вывода уравнения pvn = const уходят в анализ работы реальных поршневых машин (паровых и компрессоров). При анализе их работы снимали индикаторную диаграмму p = f(x), где х – ход поршня. От индикаторной диаграммы всего один шаг до p – v диаграммы.
Показатель политропы n в уравнении pvn = const в сущности отражает интенсивность изменения параметров в процессе, т.е. характер смены состояний. А параметры изменяются под влиянием внешних воздействий q и w на термодеформационную систему. Поэтому мы в праве ожидать, что n = n(q,w). Проверим это ожидание.
Исходное уравнение политропы pvn = const в логарифмической форме
lnp = -nlnv + const
после дифференцирования принимает вид:
dp/p = -n dv/v или n = -vdp/pdv
Иными словами, показатель политропы n есть отношение элементарной работы проталкивания к элементарной работе деформации (сжатия или расширения) и зависимость для идеального газа принимает вид:
n = (cdT – cpdT) / (cdT – cvdT) = (c – cp)/(c – cv)
Следовательно, показатель политропы n для идеального газа получил вполне определенный смысл – это функция теплоемкостей.
c ≡ cn = (ncv –cp) / (n – 1) = cv (n – k) / (n – 1)
где величина k ≡ ср/сv носит название коэффициента Пуассона[18] и является показате-
лем адиабаты. Для двухатомных газов k ≈ 1,4. Так как n = const и k = const, то выражение справедливо и для средней политропной теплоемкости:
cn|t1t2 = cv|t1t2(n – k) / (n – 1), k = cp|t1t2 / cv|t1t2
Если индикаторная диаграмма обработана, то
pvn = const или p1v1n = p2v2n и p1/p2 = (v2/v1)n
для любых двух состояний процесса. Для рабочих тел, у которых уравнения состояния или сложны, или, чаще, просто отсутствуют, найти связь температуры Т с другими параметрами состояния р или v аналитическим путем невозможно.
Для идеального газа, т.е. кроме связи pvn = const еще справедлива связь pv = RуT, сочетание этих зависимостей позволяет получить взаимосвязь:
T1 / T2 = (v2 / v1)n-1 = (p1 / p2)(n-1)/n
Замечание. Вывод связей предлагаем провести самостоятельно.
Частные политропные процессы.
Если какой-то параметр состояния при взаимодействии с внешней средой фиксировать, то процесс, входящий в гамму политропных, называют частным:
pvn = const и p = const → n = 0 – изобарный,
а для идеального газа из (3.8) T1/T2 = v1/v2.
pvn = const и v = const → n = ± ∞ – изохорный,
а для идеального газа из (3.8) T1/T2 = p1/p2.
pvn = const и T = const – изотермический, а для идеального газа n = 1 и из (3.8) v2/v1 = p1/p2.
При s = const → n = k ≡ cp / cv – изоэнтропийный (адиабатный) с уравнением pvk = const.
Замечание. Условие Q (q) = 0 (нет источников теплоты) означает, что Tds ≡ 0 и s = const и по первому признаку процесс назван адиабатным (adiabatos – непереходимая – в смысле тепловой изоляции)
На рис. 2.15. представлены графики политроп с различными показателями n для частных процессов, только еще раз напомним, что величина показателя адиабаты для двухатомных газов k ≈ 1,4.
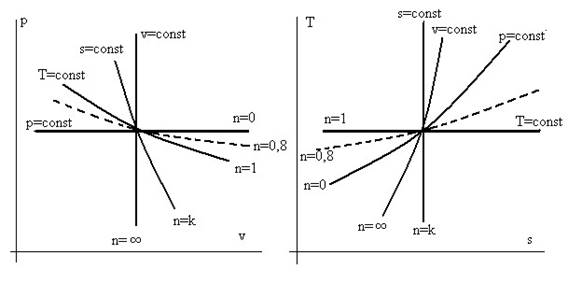
Рис. 2.15. Взаимное расположение частных политропных процессов в осях p – v и T
– s при различных значениях показателей политропы n.
Замечание. Если необходимо построить график оригинального политропного процесса, т.е. не совпадающего с указанными частными, то, зная величину n , не сложно построить этот график на фоне частных процессов.
Пример. Построить график политропного процесса с показателем политропы n =
0,8 в осях p – v и T – s.
Решение этой задачи основано на том обстоятельстве, что линии частных процессов делят всю плоскость с координатными осями на сектора. Следовательно, график (в осях p – v или T – s) политропного процесса с каким-то n должен проходить в соответствующем секторе. На рис. 3.2 линия с n = 0,8 расположена в секторе между политропами n = 0 и n = 1 и обозначена пунктиром.
Очень часто в инженерных задачах и в физико-химическом исследовании процессов с рабочим телом необходимо знать только знак изменения функций состояния Δu, Δh, Δs и функций процесса q, w. Сама величина этих изменений бывает и не нужна. Для решения этой задачи существует прием, позволяющий очень просто и наглядно ответить на поставленный вопрос.
Рассмотрим рис. 2.16.
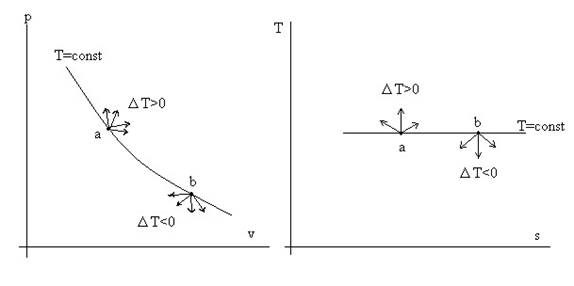
Рис. 2.16. Иллюстрация правила изотермы
На изотерме T = const возьмем произвольную точку «а». Наверное, понятно, что все процессы, выходящие из точки «а» на изотерме «вверх» (см. диаграмму T – s), характеризуются ростом температуры ΔT > 0. Зато все процессы, выходящие из точки «в» «вниз» (опять см. диаграмму T – s), дают ΔT < 0.
Рассмотрим рис. 2.17.
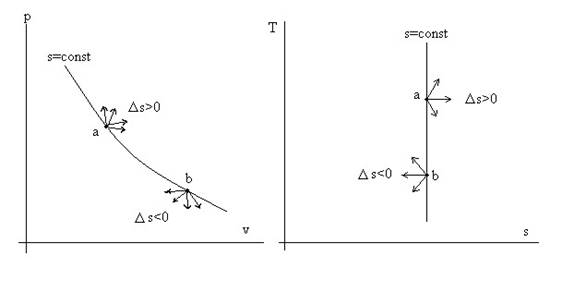
Рис. 2.17. Иллюстрация правила адиабаты
На адиабате s = const возьмем произвольную точку «а». Все процессы, выходящие из т. «а» вправо (см. диаграмму T – s), характеризуются ростом энтропии Δs > 0. Все процессы, выходящие из точки «в» влево (опять см. диаграмму T – s) характеризуются уменьшением энтропии Δs < 0.
Практическую работу правила изотермы и адиабаты проиллюстрируем на примере.
Пример. Определить знаки изменения энтропии Δs, функций состояния Δu, Δh и функций процесса q и w для процесса расширения идеального газа с показателем политропы n = 0,8.
Решение. Строим политропу с показателем n = 0,8 на фоне частных, характерных процессов в одной какой-нибудь диаграмме или в обеих p – v и T – s так, как рекомендовано выше. Точку «а» располагаем на плоскости диаграммы произвольно (см. рис. 2.18).
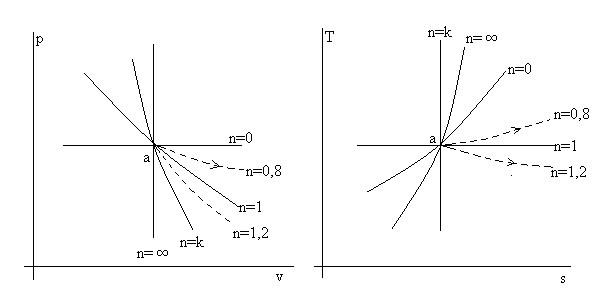
Рис. 2.18. Иллюстрация применения правила изотермы и адиабаты при решении задачи
1. Отмечаем, что по условию Δv > 0 (расширение). Следовательно, w > 0.
2. Глядя на рис.2.18, видно, что ΔT > 0 и Δs > 0.
3. Из условия ΔT > 0 следует, что Δu > 0 и Δh > 0 (du = cvdT, dh = cpdT, cv,cp > 0).
4. Из условия Δs > 0 следует, что q > 0 (dq = Tds, T > 0).
Ответ: Δu, Δh, Δs, q, w > 0, т.е. все изменения строго положительны, и качественный анализ процесса завершен.
Замечание. Если в предыдущей задаче сделать n = 1.2 и по-прежнему рассмотреть расширение газа, то ΔТ < 0, а Δs > 0. Тогда ответ задачи: Δu < 0, Δh < 0, Δs > 0, q > 0, w > 0, т.е. при росте энтропии (теплота подводится) температура уменьшается (за счет совершаемой работы над окружающей средой).
Замечание. Вся сложность применения правила изотермы и адиабаты только в грамотном расположении политропы на фоне частных политроп с n = 0, 1, k и ∞, помятуя, что k = 1,3 – 1,6 (для одно – трех атомных газов).
Весь предыдущий материал показывает, что аппарат термодинамики позволяет рассчитать любой процесс наиболее просто для идеального газа. Достаточно знать показатель политропы n, иметь таблицы теплоемкостей, и буквально на кончике пера получаем все количественные результаты с большой точностью.
Как только молекулы вещества станут близко друг к другу, так сразу их поведение начинает определяться силами взаимодействия (притяжения или отталкивания), приходится считаться с ее размерами и пространственным строением реального конгломерата. С точки зрения термодинамики это означает, что во внутреннюю энергию u(s,v) входит теперь не только кинетическая энергия поступательного движения молекул (как целого), но и потенциальная энергия взаимного расположения молекул, еще и кинетическая энергия вращения молекул и колебательных движений ее частей.
Истинные физические свойства веществ проявляются прежде всего в своем фазовом состоянии – газ (пар), жидкость или твердое. И все эти три фазы на практике используются в качестве рабочих тел. Фазами в термодинамике названы однородные (гомогенные) части системы (рабочего тела), одинаковые по своим свойствам. Обычные фазы – твердое, жидкое и газообразное (пар).
Сложность термодинамического и математического анализа этих состояний вещества и процессов с ними состоит в отсутствии или чрезвычайной громоздкости их уравнений состояния. Как известно из физики, одно из таких уравнений – это уравнение Ван дер – Ваальса[19]:
(p + a/v2)(v – b) = RуT.
Существует справочная литература, в которой для многих веществ указаны коэффициенты, а и b этого уравнения. Несложно увидеть, что это уравнение нелинейное, параметр состояния v входит в уравнение в третьей степени. Существуют и более сложные уравнения.
Всего же сейчас их насчитывается свыше 300 для различных веществ. Например, для H2O – самого распространенного на земле вещества и самого используемого человеком – в фазе пара уравнение состояния содержит 13 нелинейных слагаемых.
Как же используются такие уравнения для термодинамического расчета процессов с реальными рабочими телами? Специализированные научно-исследовательские организации изучают физические свойства рабочих тел, создают математические модели (уравнения состояния), проверяют эти модели на эксперименте в достаточно больших интервалах изменения параметров. Инженерным продуктом таких научных работ являются диаграммы состояния или таблицы. Входом в эти таблицы являются термодинамические параметры состояния – давление р и/или температура Т, а наполняются эти таблицы числовыми значениями параметров и функций состояния: энтропии s, удельного объема v, энтальпии h для различных фазовых состояний.
Рассмотрим фазовые диаграммы p – v и T – s в их типичном виде, т.е. для многих различных веществ (см. рис.2.18.).
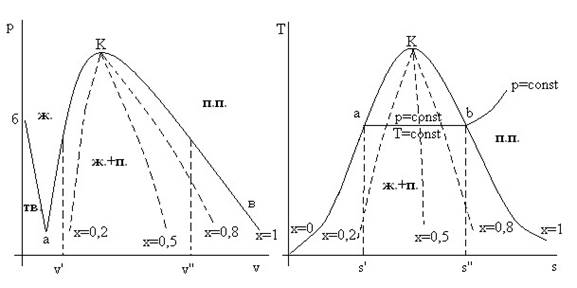
Рис. 2.18. Типичная фазовая диаграмма p – v и T – s.
тв – вещество в твердом состоянии, ж – в жидком, ж+п – влажный (насыщенный) пар, п.п. – перегретый пар. К – критическая точка.
На рис. 2.18 сплошными линиями нанесены фазовые кривые, т.е. граничные линии изменения фазового состояния вещества. Эти линии делят всю плоскость диаграммы на области, внутри которых фазовые состояния стабильны. На диаграмме p – v линия «аб» отделяет твердую фазу от жидкой, на самой линии происходит процесс плавления или затвердевания. Линия «аК» отделяет жидкую фазу от насыщенного (влажного) пара. Эту линию называют нижней пограничной кривой или линией насыщения жидкости. На самой линии «аК» отражены состояния жидкости при температуре кипения. Она разделяет состояния жидкости от состояния пара. Линия «Кв» отделяет область насыщенного пара от области перегретого пара. Еще эту линию называют верхней пограничной кривой и на ней отражены состояния сухого насыщенного пара.
Определение. Влажным (насыщенным) паром называется механическая смесь кипящей жидкости и сухого насыщенного пара.
Следствие. Все свойства насыщенного пара обладают аддитивностью свойств частей,
т.е. свойств кипящей жидкости и свойств сухого насыщенного пара.
Все параметры насыщенного состояния жидкости обозначаются буквой с одним штрихом:
v΄, s΄, h΄, u΄.
Соответственно, все параметры состояния сухого насыщенного пара обозначаются буквой с двумя штрихами:
v΄΄, s΄΄, h΄΄, u΄΄.
Все параметры состояния перегретого пара вещества обозначены так же, как и газа,
v, s, h, u,
и этим подчеркивается термодинамическая общность пара и газа. Иногда, пар называют газом, близким к состоянию насыщения.
Определение: Степенью сухости влажного (насыщенного) пара называется отношение массы сухого насыщенного пара к массе влажного пара:
х = mc.н.п. / mвл.п. кг сухого нас. пара / кг вл. пара
Из определения степени сухости х влажного пара следует, что линия «аК» на рис.3.6 слева и линия «оК» справа – это линия х = 0 (здесь находится только жидкая фаза). Соответственно, линия «Кс» на обеих диаграммах рис.3.6 – это линия х = 1 (жидкой фазы нет, только сухой насыщенный пар).
Рассмотрим ход характерных процессов на фазовых диаграммах p – v и T – s (см. рис. 2.19).
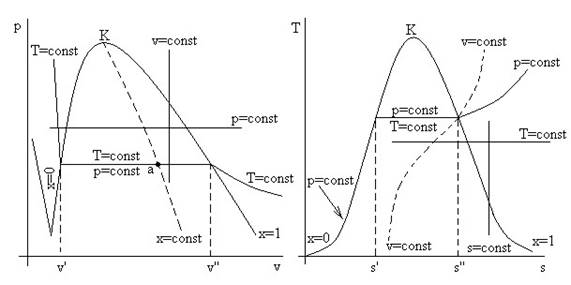
Рис. 2.19. Характерные процессы на фазовых диаграммах.
Показаны траектории процессов p = const, v = const, T = const, s = const. В области насыщенного (влажного) пара изотерма и изобара совпадают.
Для каждой изотермы (изобары) в области влажного пара на рис.3.7 показаны параметры состояния v΄ и v΄΄ и s΄ и s΄΄ - параметры состояния кипящей жидкости и сухого насыщенного пара соответственно. Зная эти величины, не сложно найти параметры состояния любой точки на изотерме (изобаре) между фазовыми кривыми. Здесь будем пользоваться определением степени сухости влажного пара и аддитивностью его свойств:
vx = (1 – x)v΄ + xv΄΄,
sx = (1 – x)s΄ + xs΄΄ = s΄ + xr / T,
hx = (1 – x)h΄ + xh΄΄ = h΄ + xr,
ux = (1 – x)u΄ + xu΄΄ или ux = hx + pvx. (3.12)
Для s, u, h в любом фазовом состоянии берутся их условные значения, сведенные в таблицах «Термодинамические свойства веществ».
Ниже, для примера, представлен фрагмент таблицы насыщенного водяного пара (по давлениям).
|
P бар |
t, oC |
v’ м3/кг |
v’’ м3/кг |
ρ’’ кг/м3 |
h' кДж/кг |
h’’ кДж/кг |
r кДж/кг |
s' кДж/кг К |
s'’ кДж/кг К |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
10 |
179.88 |
0.00113 |
0.1946 |
5.139 |
762.7 |
2778 |
2015 |
2.138 |
6.587 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
16 |
201.36 |
0.00116 |
0.1238 |
8.080 |
858.3 |
2793 |
1935 |
2.344 |
6.422 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
Таб. 2.3. Насыщенного водяного пара (по давлениям)
В справочной литературе существуют аналогичные таблицы насыщенного пара вещества по температурам. Зная давление или температуру вещества, по таблицам можно определить его параметры в состоянии фазового перехода, а далее рассчитать параметры состояния влажного пара при любом х.
Использование таблиц объясняется сложностью работы расчетчиков с громоздкими уравнениями состояния.
Эту методику продемонстрируем на конкретном примере: рассмотрим изохорный процесс v = const и рабочее вещество – Н2О (μ = 18 кг/кмоль), а рассчитывать процесс будем дважды, сначала как для идеального газа, потом как для реального вещества.
Текст задачи. В реакторе объемом V = 0,75 м3 под давлением р1 = 10 бар и при температуре t1 = 1800С находится вода в количестве m = 3,85 кг. При подводе внешней теплоты давление поднимается до р2 = 16 бар. Определить температуру t2 в конце нагрева, количество подведенной теплоты и изменение энтропии.
Решение (Н2О – идеальный газ).
1. Температура воды в реакторе в конце процесса нагрева:
v = const → T2 / T1 = p2 / p1 → T2 = T1p2 / p1 = (273 + 180)16 / 10 = 724K = 4510C.
2. Количество подведенной теплоты:
Q = mq = mcv|t1t2(t2 – t1).
По таблицам теплоемкостей для водяного пара имеем:
μсp|0180 = 34,195 кДж/кмольК, μсp|0451 = 35,364 кДж/кмольК.
Тогда средняя изобарная массовая теплоемкость равна:
cp|180451 = (μcp|0t2t2 – μcp|0t2t1) / μ(t2 – t1) = (35,364*451 – 34,195*180) / 18(451 – 180) = 1,972 кДж/кгК.
По уравнению Майера находим среднюю изохорную массовую теплоемкость:
cv|180451 = cp|180451 – R/μ = 1,972 – 8,314 / 18 = 1,512 кДж/кгК.
Окончательно, Q = 3,85*1,512*(451 – 180) = 1577,5 = 1580 кДж.
3. Изменение энтропии за процесс нагрева:
Δs = cv|t1t2 lnT2/T1 = 1,512 ln (273 + 451)/(273 + 180) = 0,70897 = 0,709 кДж/кгК.
ΔS = m*Δs = 3,85*0,709 =2,73 кДж/К.
Ответ: t2 = 4510C, Q = 1580 кДж, ΔS = 2,73 кДж/К.
Решение (Н2О – реальное вещество).
Решать будем с помощью таблиц для воды (см. фрагмент таблицы, представленный выше).
1. Начальное состояние воды. Известно, что
р1 = 10 бар и v1 = V/m = 0,75/3,85 = 0,1948 = 0,195 м3/кг = const.
По таблицам насыщенных паров воды (по давлениям, т.к. дано р1 = 10 бар, см. выше фрагмент таблицы насыщенных паров воды) определяем температуру фазового перехода
tнас = 179,880С. Одновременно, обращаем внимание, что v΄΄ = 0,1946 м3/кг. Получилось, что
tнас = 179,880С ≈ 1800С и v΄΄ = 0,1946 м3/кг ≈ v1 = 0,195 м3/кг.
Следовательно, в начальном состоянии вода находится в состоянии сухого насыщенного пара.
2. Температура в реакторе после нагрева.
Определяем состояние воды после нагрева. При р2 = 16 бар по той же таблице имеем v΄΄ = 0,1238 м3/кг. Но при v = const v2 = 0,195 м3/кг. Следовательно, v΄΄ < v2, и делаем вывод: в конце процесса нагрева вода находится в состоянии перегретого пара.
Открываем таблицу перегретого пара для воды, зная, что р2 = 16 бар и v2 = 0,195 м3/кг, находим величину температуры: t2 = 4160C.
3. Количество подведенной теплоты в процессе нагрева реактора.
q = u2 – u1, т.к. v = const. u = h – pv.
u1 = h1 – p1v1 = h΄΄(p1 = 10 бар) – p1v1 = 2778 – 10*105*0,195*10-3 = 2583,4 = 2580 кДж/кг.
Здесь величину h1 = h΄΄ = 2778 кдж/кг взяли из той же таблицы насыщенного водяного пара, а v1 = v = 0,195 м3/кг. Величина 10-3 во втором слагаемом просто переводит размерность его в кДж/кг.
u2 = h2 – p2v2 = 3288,2 – 16*105*0,195*10-3 = 2976,8 = 2980 кДж/кг.
Здесь величину h2 = 3288,2 кдж/кг нашли по таблице для перегретого водяного пара при р2 = 16 бар и v2 = 0,195 м3/кг. Отсюда
q = 2980 – 2580 = 400 кДж/кг. Q = 3,85*400 = 1540 кДж.
4. Изменение энтропии: Δs = s2 – s1 = s2 – s΄΄(p1 = 10 бар) = 7,283 – 6,587 = 0,696 кДж/кгК.
ΔS = m*Δs = 3,85*0,696 = 2,6796 = 2,68 кДж/К.
Ответ: t2 = 4160C, Q = 1540 кДж, ΔS = 2,68 кДж/К.
Сравнивая ответы решения одной и той же задачи для водяного пара как идеального газа и как реального вещества, видно, что погрешность расчета Q и ΔS находится в нормальных пределах (2 – 3)%, как это принято в химической технологии. Зато погрешность определения температуры t2 великовата:
δt2 = Δt2/t2 = (451 – 416)/416*100% = 8,4%.
На рис. 2.20 приведена иллюстрация решения задачи двумя способами.
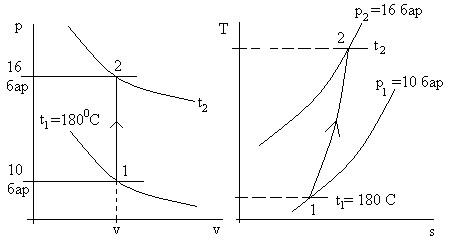
Рис. 2.20а. Изображение процесса в рассмотренной задаче в осях р – v и T – s. H2O – идеальный газ. Величины Т2, q ,Δs – искомые.
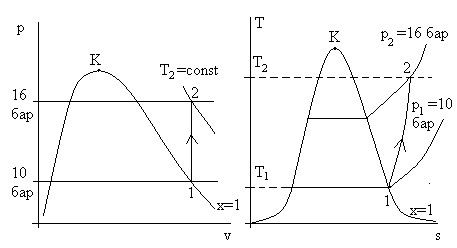
Рис. 2.20б. Изображение процесса в рассмотренной задаче
в осях p – v и T – s. H2O – реальное вещество. Величины Т2, q, Δs – искомые.
Замечание. Методика расчета процессов с реальными веществами по таблицам кажется сложной только в том, что сначала надо определить фазовое состояние вещества в начальной и конечной точке процесса, а потом уже пользоваться соответствующими таблицами для поиска необходимых термодинамических величин. Использование фазовых диаграмм для расчета процессов вообще трудностей не представляет, хотя точность расчета меньше, чем при пользовании таблиц.
Тема 2.4. Термодинамические процессы и циклы
Еще более 200 лет назад развитие промышленности поставило перед учеными и инженерами задачу непрерывного получения механической работы, работы упорядоченного движения рабочего тела. А на 100 лет позже пришлось поставить задачу непрерывного «получения холода» за счет работы (т.е. переноса теплоты от тел с нижнего температурного уровня на верхний).
Однако, получать работу или трансформировать ее в теплоту непрерывно в разомкнутом, одностороннем процессе – невозможно, хотя бы потому, что односторонне движущийся поршень в цилиндре неработоспособен (должен быть ∞ ход его). Поэтому необходимость циклов, как замкнутой системы процессов, для человеческой практики была давно понята, особенно при переходе к непрерывным технологическим процессам.
Определение. Циклом называется замкнутый (круговой) процесс.
Применение циклов создает условия возвращения рабочего тела в исходное состояние. Рассмотрим рис. 2.21.
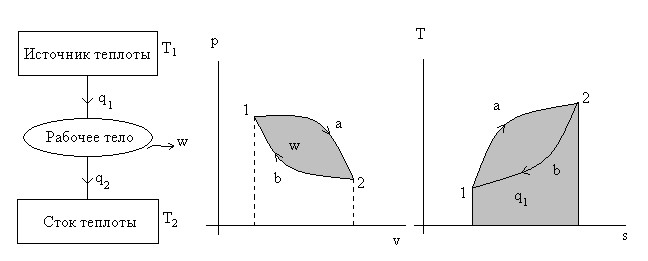
Рис. 2.21. Иллюстрация работы тепловой машины (Т1 > Т2)
В точке 1 на диаграммах p – v и T – s рабочее тело начинает контактировать с источником теплоты (верхний температурный уровень). Далее, в процессе 1а2 происходит расширение рабочего тела и одновременно приход теплоты q1 от источника к рабочему телу. В точке 2 прекращается контакт с источником, который отдал теплоту q1, и организуется контакт рабочего тела со стоком теплоты (холодильником). В процессе 2в1 происходит сжатие рабочего тела с затратой работы и одновременно отдача теплоты q2 холодильнику. Так, организуя контакт то с источником, то с холодильником, рабочее тело возвращается в исходное состояние т. 1 (здесь тепловой машине не требуется длинных цилиндров, будет короткий ход поршня).
Отметим важное обстоятельство на рис. 2.21: линия расширения 1а2 расположена на диаграмме p – v выше линии сжатия 2в1, следовательно, работа расширения будет больше работы сжатия (по абсолютной величине), следовательно, работа за цикл w > 0. Такие циклы получили название циклов тепловых машин (двигателей) или прямые циклы (а будут еще обратные). Просто в прямых циклах теплота превращается в работу, а в обратных (холодильных) работа в теплоту.
Рассматривая свойства внутренней энергии в лекции 1, было показано, что
q1 – q2 = q = w кДж/кг
Определение. Термическим коэффициентом полезного действия технического устройства называется отношение количественно выражаемых пользы и затрат.
Следовательно, термический коэффициент полезного действия ηt теплового цикла равен ηt = w/q1 = (q1 – q2)/q1 = 1 – q2/q1 кДж работы/кДж затраченной теплоты.
Здесь q1 – количество теплоты, взятого из источника рабочим телом, q2 – количество теплоты, отданного холодильнику.
Величина ηt является количественной мерой совершенства, эффективности термодинамического цикла. Из (4.4) следует, что, чтобы ηt → 1, необходимо или q2 → 0 и / или q1 → ∞. Первое требование проблематично, второе – практически не реализуемо.
Рассмотрим цикл холодильной машины (или обратный цикл) на рис. 2.22.

Рис. 2.22. Иллюстрация работы холодильной машины (Т1 > Т2)
В состоянии 1 рабочее тело приводится в контакт со стенками холодильной камеры, отводя из нее теплоту q2 при совершении работы расширения в процессе 1в2. В состоянии 2 рабочее тело уже начинает контактировать с источником теплоты и в процессе 2а1 отдает теплоту q1, забирая из внешней среды работу сжатия w. Таким образом, создавая контакт то с холодильной камерой, то с источником теплоты рабочее тело возвращается в исходное состояние т.1. При этом теплота q2 переносится с нижнего температурного уровня Т2 на верхний Т1.
В этих циклах (их назвали холодильными) процесс расширения 1в2 в диаграмме p – v расположен ниже процесса сжатия 2а1 рабочего тела. Поэтому приходится подводить к циклу работу w из внешней среды. Это обстоятельство обусловило название холодильных циклов как обратных по отношению к тепловым (прямым).
Количественной мерой совершенства холодильного цикла является аналог термического коэффициента полезного действия, который в холодильной технике носит название холодильного коэффициента:
εх = польза/затраты = q2/w = q2/(q1 – q2) кДж «холода»/кДж работы. (4.5)
Замечание. Холодильный цикл на рис. 2.22. термодинамически ничем не отличается от цикла теплового насоса, но последний называют такой цикл, который используется для отопления подводом теплоты q1 за счет работы.
Определение. Тепловым насосом или динамическим отоплением называют процесс получения теплоты за счет затрачиваемой работы.
И в холодильной машине, и в тепловом насосе рабочее тело переносит теплоту к телам с высокой температурой Т1 от тел с низкой Т2 за счет затрачиваемой работы.
Сади Карно[20] поставил принципиальный вопрос: из каких процессов должен состоять цикл тепловой машины, которая бы обеспечивала максимальную эффективность. Здесь Карно руководствовался правилом: «экономично – самое простое».
Если посмотреть на рис. 2.21, то видно, что подвод теплоты q1 в процессе 1а2 и отвод теплоты q2 от рабочего тела в процессе 2в1 происходят при переменных температурах. Т.е. надо иметь много источников и стоков теплоты с разными температурами для проведения квазистатического (обратимого) процесса. Это очень сложно, а значит – дорого. Самое простое сделать один источник теплоты с температурой Т1 и один теплоприемник с температурой Т2. Следовательно, процессы 1а2 и 2в1 должны быть изотермическими, а во внешней среде должны быть только два тела, с которыми осуществляется теплообмен с рабочим телом. Чтобы обеспечить это «только», переход с одного температурного уровня на другой для замыкания цикла придется осуществлять адиабатичным (теплоизолированным). А для обратимых процессов адиабатичность означает изоэнтропность (S = const). Так стремление к максимальной простоте привело Карно к изобретению цикла, в дальнейшем названным его именем (см. рис. 4.3)
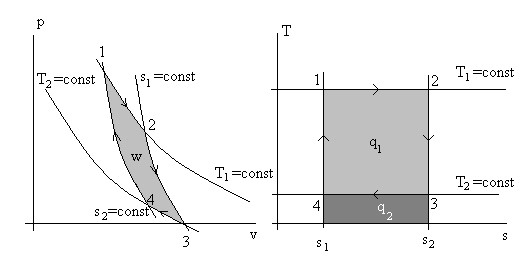
Рис. 2.23. Иллюстрация цикла Карно в термодинамических диаграммах p – v и T – s. Количество подведенной теплоты q1 и количество отведенной q2 представлены площадками с разной штриховкой.
Рассмотрим термический коэффициент полезного действия ηtк цикла Карно. Согласно
(4.4) ηtк = 1 – q2/q1 = 1 – T2Δs/T1Δs = 1 – T2/T1, Δs = s2 – s1.
Соответственно (4.3) холодильный коэффициент εхк холодильного цикла Карно равен
εхк = q2/(q1 – q2) = T2Δs/(T1Δs – T2Δs) = T2/(T1 – T2).
Технологическая схема, реализующая цикл Карно, показана на рис. 2.24.
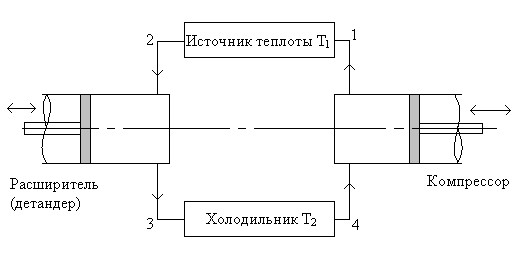
Рис. 2.24. Технологическая схема, реализующая тепловой цикл Карно. Точки 1, 2, 3, 4 соответствуют этим же точкам на диаграммах p – v и T – s на рис.(2.23).
Рассмотрим этот цикл, считая, что рабочее тело – идеальный газ. В процессе 1 – 2 Т1 = const . Следовательно, Δu = q – w = 0 и q = w. Т.е. вся теплота из источника теплоты q1 переходит в работу расширения w12. В процессе 2 – 3 надо «опуститься» на нижний температурный уровень Т2 адиабатно (s2 = const), следовательно, q23 = 0 и все изменение внутренней энергии в процессе переходит снова в работу расширения, т.к. Δu23 = -w23.
Здесь вспомним, что в процессе 2 – 3 dT < 0 → Δu23 < 0 → w23 > 0, т.е. рабочее тело отдает работу расширения во внешнюю среду.
В процессе 3 – 4 происходит изотермическое сжатие. Снова dT = 0 → Δu34 = 0 → q34 = q2 = w34 < 0. Здесь теплота q2 уходит во внешнюю среду (в холодильник) и внешняя среда тратит работу сжатия w34.
Последний процесс 4 – 1 это процесс возврата рабочего тела в исходное состояние, в т. 1. Процесс адиабатный (s1 = const). Здесь dT > 0, Δu41 > 0 → Δu41 = -w41 → w41 < 0,т.е. внешняя среда тратит работу на сжатие в компрессоре.
Выбор процессов, образующих цикл Карно, замечателен тем, что то dT = 0, то ds = 0,
т.е. то du = 0, то dq = 0. И при такой комбинации процессов, образующих цикл Карно, наиболее просто получать работу во внешнюю среду и наиболее экономичны сами энергетические результаты (полнота обращения теплоты и внутренней энергии в работу и обратно).
Эта теорема была доказана Клаузиусом через полвека после публикации идей Карно в 1824 году. Результаты доказательства теоремы Карно для теплового двигателя были естественным путем перенесены на холодильный цикл Карно.
Теорема Карно содержит три результата:
1. Термический коэффициент полезного действия определяется выражением ηtк = 1 – q2/q1 = 1 – T2Δs/T1Δs = 1 – T2/T1, Δs = s2 – s1.
2. Термический коэффициент полезного действия не зависит от свойств рабочего тела.
3. Термический коэффициент полезного действия максимален среди всех других циклов в тех же температурных пределах.
Доказательство первого утверждения уже проведено в ηtк = 1 – q2/q1 = 1 – T2Δs/T1Δs = 1 – T2/T1, Δs = s2 – s1.
Доказательство второго состоит в следующем. Зададимся вопросом: «В каких параметрах состояния, в каких функциональных связях непосредственно проявляются теплофизические свойства конкретных, индивидуальных веществ?». Ответ на вопрос таков: изменение энтропии рассчитывается через среднюю массовую теплоемкость вещества, а она является характеристикой этого вещества. Далее, уравнения состояния, т.е. зависимость потенциала какого-то рода от всех координат состояния, индивидуально для каждого вещества в любой фазе. Это тоже носитель свойств вещества. Таким образом, изменение энтропии Δs в любом процессе сильно зависит от свойств вещества. Но в связи с тем, что величина Δs входит и в числитель и в знаменатель в выражении для ηtк, то эту величину можно сократить, и эта процедура строга математически. Отсюда и следует, что величина термического коэффициента полезного действия ηtк не зависит от свойств рабочего тела, носитель свойств Δs исчезла из выражения для ηtк.
Доказательство третьего утверждения получим из рассмотрения рис. 2.25.

Рис. 2.25. Иллюстрация к доказательству максимальности термического коэффициента полезного действия цикла Карно.
На рис. 2.25 показана диаграмма T – s , изображен цикл Карно и любой (произвольный) цикл в тех же температурных пределах Т1 и Т2. Вспомним, что
ηtк = 1 – q2 / q1,
где q1 – количество теплоты, полученной рабочим телом в источнике теплоты, q2 – количество теплоты, отданной рабочим телом в холодильнике.
Глядя на рис. 4.5 видно, что q2 > q2к на величину заштрихованной справа налево площади под графиком. Здесь q2 – отданная теплота в холодильнике любого цикла, q2к – то же, но в цикле Карно. Аналогично, видно, что q1к > q1, поэтому в целом ηtк > ηt для любого цикла, вписанного в цикл Карно. Теорема Карно доказана.
Пример. Температура вспышки паров бензина в двигателе внутреннего сгорания (ДВС) равна примерно 20000С, а температура атмосферы летом 200С. Найти термический коэффициент полезного действия двигателя ДВС, работающего по циклу Карно.
Решение. ηtк = 1 – Т2 / Т1 = 1- (20 + 273) / (2000 + 273) = 0,87 = 87%. Ответ: ηt = 87%. Это значит, что, залив в бак автомобиля 100 л бензина, 87 л пойдут на движение автомобиля, а 13 л будут истрачены на нагрев атмосферы. Реально ηt ≈ 35% для лучших бензиновых ДВС. Следовательно, из 100 л бензина в баке только 35 л будут истрачены на движение, остальное – на рост энтропии в атмосфере. Хорошие дизельные двигатели (танковые, тяжелых грузовиков и т.д.) имеют коэффициент полезного действия ≈ 50%. Это предопределило превосходство советских танков над германскими бензиновыми во время Великой Отечественной войны и ускорило победу над германским фашизмом.
Самые совершенные (современные) паросиловые установки имеют ηt ≈ 42 – 45 %. Это означает, что из 100 вагонов угля, добытых в шахте и привезенных до ТЭЦ, меньше половины будут превращены в электроэнергию, а остальные пойдут на рост энтропии в окружающей среде. Печально, но факт!
Генетической особенностью любых циклов (и прямых, и обратных, см. рис. 2.21 и 2.22) является необходимость вернуть рабочее тело в исходное состояние. Но сделать это без отдачи теплоты в холодильнике неосуществимо.
Можно провести цикл совершенно обратимым путем, с большей или меньшей степенью необратимости, но особенность, заключающаяся в отдаче части теплоты рабочим телом в теплоприемнике низкой температуры, свойственна циклу при всех обстоятельствах.
Именно поэтому нельзя осуществить тепловой цикл с одним источником теплоты (вечный двигатель второго рода), именно поэтому нельзя получить эффективность ηt = 1 (а при электрическом взаимодействии рабочего тела с внешней средой – можно).
Замечание. Еще раз подчеркнем, что этот вывод никакого отношения ко второму закону термодинамики не имеет.
Тема 2.5. Термодинамика потоков
Термодинамический метод анализа интересующего нас объекта начинается с того, что сам объект отгораживается от внешней среды некоторой абстрактной границей «Х». Далее, договариваемся о направлении нормали n к этой границе: пусть, например, она направлена во внутрь объекта. Все, что находится внутри границы «Х», мы назвали термодинамической системой, все, что снаружи – внешняя среда.
Следующий шаг в термодинамическом методе анализа – установление видов, родов взаимодействия системы с внешним миром. Установить – означает понять физический смысл взаимодействия, определить для каждого из них потенциал Р и координату состояния х. Это самый трудный и самый ответственный этап метода термодинамического исследования. Дальше начинает работать аппарат, инструментарий метода: записываем в единой форме (т.е. для любых объектов исследования) первый закон термодинамики - изменение внутренней энергии системы равно алгебраической сумме всех количеств воздействия.
Напомним, что элементарным количеством воздействия данного рода называется произведение потенциала этого рода на дифференциал его сопряженной координаты.
После записи первого закона термодинамики осталось попросить физиков дать уравнения состояния для термодинамической системы.
Напомним, что уравнением состояния называется функциональная зависимость потенциала какого-то рода от всех координат состояния.
Следовательно, сколько родов взаимодействия, столько потенциалов и координат состояния, столько количеств воздействия, столько слагаемых в правой части уравнения первого закона термодинамики.
Разработка базиса, фундамента для проведения термодинамического анализа объекта на этом заканчивается. Осталось «пожинать» плоды, если владеешь инструментарием математического анализа.
Слово «сжимаемых» в названии главы очень важно: оно означает, что мы не рассматриваем гидравлику, которая имеет дело с потоком жидкостей, т.е. несжимаемых сред.
На рис. 2.26 представлена схема изучаемого объекта. Границей «Х», согласно рис.
2.26, является поверхность канала и две плоскости на торцах при х = 0 и при х = L.

Рис. 2.26. Схема канала, по которому движется сжимаемая среда.
х – продольная линейная координата. F(x) – текущая площадь сечения, м2.
Каковы виды (роды) взаимодействия рабочего тела в канале и внешней среды? Прежде всего – термическое и деформационное, уже знакомое нам по предыдущему материалу. Потенциал и сопряженная координата их уже хорошо известны: p – v и T – s.
У изучаемой термодинамической системы есть новое качество: упорядоченное движение, характеризуемое линейной скоростью w(x), м/с.
Предостережение. Ранее, буквой w мы обозначали удельную работу среды Дж/кг. Теперь этой буквой будем обозначать линейную скорость w(x), а для работы примем допустимое по ГОСТ обозначение l Дж/кг.
Первопричиной движения потока в термодеформационной системе (см. рис. 5.1) является конечная разность давления в окружающей среде ре и в рабочем теле (системе) р: Δр = ре – р. И всегда эти давления не равны, если существует поток массы по каналу.
Согласно лекции 1, давление относится к категории сил Х, и для потенциально – силовых взаимодействий первый закон термодинамики записывается как
ΔU = ∑(P + ΔP)dx - ∑(X + ΔX)dx
Здесь U – внутренняя энергия среды, Дж, слагаемые справа – количества воздействий, Р, Х и х – потенциалы, силы и координаты состояния системы.
Уравнение ΔU = ∑(P + ΔP)dx - ∑(X + ΔX)dx – запись первого закона термодинамики для конечных разностей потенциалов ΔР и движущих сил ΔХ при неравновесных (необратимых) процессах, в которых всегда существуют побочные (некомпенсированные, вторичные) явления. Так и в нашем случае в открытой системе при конечных разностях давлений возникает движение. Это движение, упорядоченное перемещение характеризуется скоростью w, м/с, которая по своему смыслу является потенциалом кинематического взаимодействия термодинамической системы с внешней средой. Разность скоростей обусловливает появление количества движения mw = J или w = J/m = j. Тогда элементарное количество взаимодействия, по определению, равно
w*d(mw) = wdJ, Дж или wdw = dj, Дж/кг.
В открытой системе появляется (проявляется) новое воздействие как результат возникновения вторичного силового эффекта ΔР = Ре – Р. Напомним, что в закрытой системе нет обмена массой с внешней средой, нет химических превращений. Поэтому разность давлений Δр создавала только деформацию (сжатие или расширение) объема ΔV. В итоге вторичный эффект в открытой системе от силового воздействия (давления) описывается как
ΔХ*dx = w*dj, Дж/кг.
Вторичный эффект иного рода – тепловой – относится к работе сил трения lтр на границе потока и канала и сил трения в объеме потока из-за существования поля скорости по радиусу канала. Работа сил трения lтр всегда приводит к росту (генерации) энтропии (см. лекцию 4). Происходит диссипация (рассеяние) энергии. Этот суммарный эффект (рост энтропии и от трения потока о стенки канала, и от трения в объеме потока) будем учитывать общим членом Tds (напомним, что энтропия s является координатой состояния термического взаимодействия системы с внешней средой).
Окончательно, из ΔU = ∑(P + ΔP)dx - ∑(X + ΔX)dx получаем
du = Tds – wdj – dlтр – dlпотока
Иными словами, данное выражение представляет собой общую форму записи первого закона термодинамики: изменение внутренней энергии системы равно сумме всех внешних воздействий, в котором первое слагаемое справа – все формы теплообмена рабочего тела в канале с внешней средой; второе – воздействие подвижной среды – массы движущегося газа, в объеме которого происходит работа потока (четвертое слагаемое); третье – работа сил трения.
Возможно и пятое слагаемое – техническая работа lтехн перемещения самого канала во внешней (окружающей) среде, как это происходит с ракетой, с самолетом с ракетными двигателями, с газовой или паровой турбиной.
В итоге поток сжимаемой среды в канале характеризуется изменением кинетической энергии поступательного движения (ее упорядоченная форма)
d(δm w2/2) = wd(δm w),
где δm = f(x) – элементарная масса в произвольном сечении х в бесконечно малом
объеме F(x) dx канала (см. рис. 5.1).
На формирование, разгон и движение потока необходима энергия, которая получается за счет работы проталкивания газа (пара) по каналу. Проталкивание обеспечивается давлением подготовленного газа при поступлении к входному сечению канала х = 0 (см. рис. 5.1). Подготовка происходит или в компрессоре, или в камере сгорания топлива, или в котельном агрегате по выработке пара высокого давления и температуры. Начальная скорость потока w0 = w(x = 0) принимается обычно нулевой, но иногда ее определяют чисто гидравлически: w(x = 0)< 10 – 15 м/с. Накопленная энергия
p2
Vdp
p1
для процесса сжатия в компрессоре (см. рис. 2.27 – а) ранее названа «располагаемой
работой». Теперь для потока она и есть «работа проталкивания» (см. рис 2.27 – b) – в сущности процесс обратный компрессии по формальному термодинамическому показателю: оба процесса адиабатные (без теплообмена), но один с ростом давления, а другой – с его падением.
p1 p1
Vdp Vdp
p0 p0
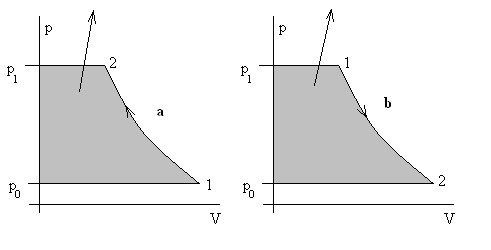
Рис. 2.27. Иллюстрация к объяснению работы проталкивания потока в канале
Первый происходит с затратой работы внешней средой (знак « – »), а второй – с отдачей работы на сторону, знак « + »).
Уравнение ΔU = ∑(P + ΔP)dx - ∑(X + ΔX)dx написано для неподвижного наблюдателя, чуть изменим его к виду:
du + d(w2/2) = δq – δlпотока – δlтрен + δlтехн
Это уравнение записано для системы координат, никак не связанной ни с потоком среды в канале, ни со стенками канала. Теперь «влезем» в физически малый объем движущегося потока F(x)dx, т.е. систему координат свяжем с самим потоком. Тогда уравнение баланса энергии запишется в обычной, знакомой уже форме:
du = δq – pdv – δqтрения ,
где теплота трения δqтрения = δlтрения. Вычтем это уравнение из (5.1 – в):
d(w2/2) = - δlпотока + pdv + δlтехнич. (5.1 – с).
Осталось только понять и раскрыть смысл полной работы потока lпотока. Этот смысл легко понять из рис. 2.28.
p0 p0
Vdp pdV .
p1 p1
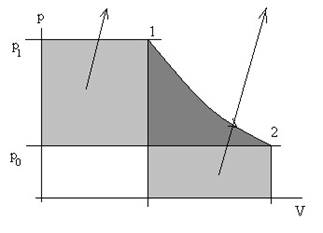
Рис. 2.28. Иллюстрация к пояснению полной работы потока
Из рис. 2.28, следует:
Lпотока = ∫Vdp + ∫pdV = ∫d(pV) = p1V1 – p0V0, Дж,
или в удельных величинах lпотока = ∫d(pv), т.е. δlпотока = pdv + vdp, Дж/кг.
Окончательно, для адиабатического потока, для неподвижного канала δlтехнич = 0 и без трения уравнение d(w2/2) = - δlпотока + pdv + δlтехнич принимает вид:
d(w2/2) + vdp = 0, Дж/кг
Уравнение d(w2/2) + vdp = 0 обычно называют механической формой описания движения потока.
Теперь вспомним, что dh = Tds + vdp = δq + vdp и что для адиабатного течения δq = 0. Тогда уравнение d(w2/2) + vdp = 0 принимает вид:
d(w2/2) + dh = 0, Дж/кг
Уравнение d(w2/2) + dh = 0 обычно называют термической формой описания движения потока.
Замечание. Посмотрим на уравнение d(w2/2) + vdp = 0 и вспомним, что v ≡ 1/ρ. Тогда получаем:
d(w2/2) + dp/ρ = 0.
Одновременно, вспомним уравнение Бернулли в курсе гидравлики:
gZ + p/ρ + w2/2 = const → ρgZ + p + ρw2/2 = const,
где Z нивелирная высота, отвечающая за статическое давление ρgZ столба рабочей жидкости в поле силы тяжести. Уравнение Бернулли можно получить из d(w2/2) + vdp = 0 интегрированием при условии ρ = const, что справедливо только для жидкостей, для несжимаемых сред. При течении газов (паров) ρ = ρ(р,Т). Кроме того, для газов (паров) ρг << ρжидк (примерно в 1000 раз), поэтому можно не учитывать статическое давление столба газа (пара) в поле сил тяжести в d(w2/2) + vdp = 0.
Уравнения d(w2/2) + vdp = 0 и d(w2/2) + dh = 0, еще далеко не образуют расчетный аппарат для поиска параметров потока газа (пара) в канале. Присоединим к этим уравнениям еще один закон, закон сохранения: сохранения массы. Его еще называют условием неразрывности (сплошности) течения.
Предварительно проведем еще одно упрощение: будем рассматривать одномерное течение, т.е. все характеристики и параметры рабочего тела в любом месте сечения F(x) (см. рис. 5.1) будем считать одинаковыми по радиусу сечения. Они теперь будут зависеть только от продольной координаты х: р = р(х), Т = Т(х), w = w(x) и т.д. Тогда массовый расход рабочего вещества в канале равен:
G = ρ(x) F(x) w(x) → G = F(x) w(x)/v(x) = const, кг/с.
Это и есть формализация закона сохранения массы в канале. Теперь это выражение прологарифмируем и далее продифференцируем:
lnF(x) + lnw(x) – lnv = lnconst → dF/F + dw/w – dv/v = 0
Данное представляет собой запись закона сохранения массы в дифференциальной форме или уравнение сплошности (неразрывности).
Замечание. Уравнение сплошности не справедливо для потока людей, идущих по коридору переменного сечения. В узкой части коридора люди уменьшают свою скорость w(x), чтобы не толкаться и не давить друг друга (вспомните толпу людей перед эскалатором в метро в часы пик). Зато молекулы газа (пара) в узкой части канала начинают двигаться быстрее.
Для газовой и паровой фазы еще справедливо уравнение адиабаты pvk = const. Опять прологарифмируем это уравнение, а затем продифференцируем его:
lnp + k lnv = ln const → dp/p + k lnv/v = 0
Наконец, если рабочее тело в канале находится в состоянии идеального газа, то еще
pv = RT → lnp + lnv – lnR – lnT = 0 → dp/p + dv/v – dT/T = 0
И одновременно в lnp + k lnv = ln const → dp/p + k lnv/v = 0 k = ср/сv для идеального газа.
Теперь напишем полную систему уравнений термодинамической модели потока газа (пара) в канале:
1. Уравнение энергии: dw2/2 + vdp = 0 или dw2/2 + dh = 0
2. Уравнение сплошности: dF/F + dw/w – dv/v = 0
3. Уравнение адиабаты: dp/p + k dv/v = 0
4. Уравнение состояния идеального газа: dp/p + dv/v – dT/T = 0
p(x = 0) = p1 и p(x = L) = p2
T(x = 0) = T1
Всего искомых функций 5: w(x), p(x), v(x), T(x), h(x) и уравнений тоже 5. С точки зрения математики модель получилась замкнутой: число уравнений и число искомых функций одинаковы (это одно из условий корректности любой математической задачи). Заметим, что функция F(x) считается известной по постановке задачи.
Перечислим и назовем все гипотезы, предпосылки и упрощения при формализации модели, чтобы не было умолчаний и была ясна область применимости модели.
1 . Считаем, что канал теплоизолирован или скорость течения так велика, что процесс теплообмена не успевает произойти. Итак, адиабатичность. Одновременно, предполагаем отсутствие трения. Тогда s = const.
2. Канал, в котором движется поток газа (пара) – неподвижен. Тогда техническая работа потока нулевая.
3. Влиянием силы тяжести пренебрегаем, т.к. плотность газа (пара) ничтожно мала по сравнению с плотностью жидкости.
4. Все параметры и характеристики потока в любом сечении канала F(x) одинаковы по радиусу и зависят только от продольной координаты х.
5. Уравнение процесса в каждом сечении F(x) – политропа с показателем n = k.
6. Если рабочее тело в канале – идеальный газ, то параметры состояния еще, кроме политропы, связаны уравнением Клайперона-Менделеева pv = RT, а k = ср/сv.
Из уравнения lnp + k lnv = ln const → dp/p + k lnv/v = 0 получаем: dp/kp = - dv/v и подставляем вместо dv/v в уравнение (5.4):
dF/F + dw/w + dp/kp = 0.
Далее, из d(w2/2) + vdp = 0 находим dp = -dw2/2v и подставляем в предыдущее уравнение:
dF/F + dw/w – w dw/(kpv) = 0.
Из курса физики известно выражение зависимости скорости звука «а» через параметры состояния вещества: kpv = a2.
А так как р = р(х) и v = v(x) для потока в канале, то а = а(х) и является местной скоростью звука (скоростью распространения возмущений в веществе). Окончательно, получаем:
dF/F + dw/w – w dw/a2 = 0 → dF/F = - (1 – w2/a2)dw/w → dF/F = - (1 – M2) dw/w.
(5.8)
Здесь М≡w/a называют в аэромеханике числом Маха, по имени известного австрийского ученого Х1Х века.
Это уравнение позволяет провести кинематическое исследование движения газа в различных условиях сопряжения со стенками канала в условиях разгона потока (dp < 0 и dw > 0) и в условиях торможения (dp > 0 и dw < 0). Действительно, разгон потока в канале вдоль оси х, это dw > 0. Если на входе в канал (х = 0 см. рис. 2.26) скорость невелика, т.е. меньше скорости звука (w(x = 0)< a), то число Маха М < 1. Следовательно, при разгоне дозвукового потока dF < 0. Канал должен сужаться (такой канал называют конфузором).
При зазвуковой скорости потока на входе в канал (w(x = 0) > a и М > 1) получаем dF > 0, т.е. канал должен расширяться (такой канал называют диффузором). На уравнение (5.8) можно посмотреть и иначе:
dw/w ~ dF/F.
Следовательно, при dF = 0 получаем dw = 0, т.е. в канале постоянного сечения (например, в трубе) скорость потока по длине канала постоянна.
Уравнение dF/F + dw/w – w dw/a2 = 0 → dF/F = - (1 – w2/a2)dw/w → dF/F = - (1 – M2) dw/w по существу содержит прямые рекомендации инженерам, которые применяют высокоскоростные потоки в технике. Действительно, для практического получения сверхзвуковых потоков необходимо соединить конфузор (dF < 0) с диффузором (dF > 0). Такое устройство называют соплом (обычно, соплом Лаваля[21] по имени его изобретателя). В химической промышленности эти устройства широко используются в центробежных компрессорах и центробежных расширителях (детандерах). Существуют аппараты для транспортировки газов и паров – инжекторы (нагнетатели газа) и эжекторы, отсасывающие газы из аппаратов. И, конечно, сопла используют в ракетной технике и авиации, как основной элемент ракет и двигателей для самолетов сверхзвуковой авиации.
На рис 2.29 представлена форма сопла Лаваля и качественное изменение параметров состояния газа (пара) вдоль сопла.
Рис. 2.29. Форма сопла Лаваля и качественное изменение параметров состояния потока вдоль сопла.
Эту связь не сложно установить с помощью уравнения d(w2/2) + vdp = 0. Если его проинтегрировать в пределах от р1 до текущего давления р и перед этим воспользоваться уравнением адиабаты:
pvk = const → p1v1k = pvk → v = v1(p1/p)1/k
то получим хорошо известный интеграл:
w2/2 = ∫vdp = k/(k – 1) [(p/p1)(k – 1)/k – 1] p1v1.
После несложных алгебраических преобразований окончательно получаем искомую связь:
w = [2k/(k – 1) p1v1(1 – β(k – 1)/k)]1/2, м/с, β ≡ p/p1
Здесь, напомним, р = р(х), т.е. текущее давление в канале с координатой х. Скорость течения потока можно получить и из уравнения d(w2/2) + dh = 0:
w = (2(h1 – h))1/2, м/с
И здесь тоже h = h(x) – энтальпия рабочего тела в канале с координатой х.
Замечание. Если обратить воздействие, т.е. вводить сверхзвуковой поток в канал типа сопло Лаваля, то скорость и кинетическая энергия потока будут убывать, а давление (и потенциальная энергия рабочего тела) будут возрастать (так работает, например, инжектор). Подобное сравнение в термодинамике именуется принципом обращения воздействия. Однако, при любых обстоятельствах течения потока направление изменения скорости и давления противоположны:
d(w2/2) + vdp = 0 → wdw + vdp = 0 → dw/dp = - v/w < 0.
Эту связь установим с помощью уравнения сплошности:
G = Fw/v, кг/с.
Подставим сюда выражение (5.9) для w и воспользуемся уравнением адиабаты pvk = const. Окончательно, получаем:
G = F{2k/(k – 1) p1/v1 [β2/k – β(k – 1)/k]}1/2, кг/с
Рассматривая данное выражение можно увидеть, что при β = 0 и при β = 1 расход G = 0. Согласно теореме Роля из математического анализа функция G = G(β) должна иметь хотя бы один экстремум. Исследуем эту функцию: возьмем производную dG/dβ и приравняем ее к 0, отсюда найдем корни βi этого уравнения, которые и определят положение экстремумов. Таких корней оказалось ровно один:
β = βк = (2/(k – 1))k/(k – 1)
А по знаку второй производной можно утверждать, что этот экстремум – максимум. Рассмотрим график зависимости G = G(β) на рис. 2.30.
Рис. 2.30. Зависимость массового расхода G(β) от степени расширения β потока в канале.
Одна из ветвей этой зависимости показана пунктиром. Эта часть кривой G = G(β) физически не реализуема. Опыт показывает, что для любых каналов, кроме сопла Лаваля, G = Gk = const при 0 < β < βk, а для сопла Лаваля справедлива кривая выше Gk = const.
Окончательно, массовый расход G потока в канале при βk < β < 1 зависит от β = р/р1,
т.е. от движущей силы процесса движения по каналу. При любых меньших β < βk для любых каналов, т. е. любой геометрической формы F(x), кроме сопла Лаваля, G = const.
Изобретение. При отоплении печей природным газом в химической промышленности и промышленности строительных материалов неизбежны колебания давления перед сопловыми устройствами подачи природного газа. Эти колебания давления чисто случайны, не зависят от действий операторов печи, так как определяются случайным числом подключенных/отключенных потребителей газа к магистральному газопроводу.
Колебания давления приводят к колебаниям расхода природного газа в печь, и при высокой калорийности газа это приводит к случайным существенным изменениям температуры в печи, что вызывает или брак производства, или аварию типа спека («козла»).
Для увеличения работоспособности печного агрегата можно поднять давление перед сопловыми устройствами так, чтобы истечение газа стало звуковым, т.е. массовый расход природного газа G кг/с станет постоянным при всех обстоятельствах. Реализация такого предложения сделала вероятность «козла» в печи нулевой и одновременно резко снизила вероятность брака целевого продукта. «Крутой» студент капиталистической чеканки может быстро оформить патент на свое имя и получать дивиденды от пользователей предложения.
Процесс течения газов в любом канале можно изобразить в диаграммах p – v и h – s (см. рис. (2.31).
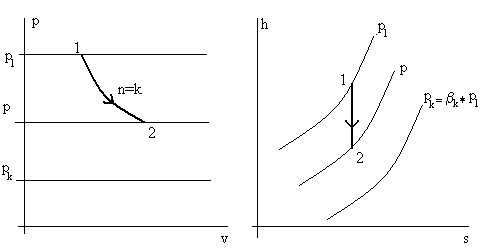
Рис. 2.31. Процесс течения газов в канале в координатах p – v и h – s при βk < β < 1.
При движении газа по соплу Лаваля давление на выходе из сопла равно давлению в окружающей среде, куда происходит истечение, и скорость истечения здесь наибольшая
(см. рис. 2.32).
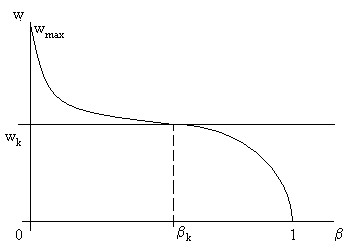
Рис. 2.32. Зависимость скорости истечения газа из сопла Лаваля от степени расширения β = р/р1.
Если истечение из сопла Лаваля происходит в вакуум, как для космических аппаратов, то р = 0 и, следовательно, β = 0. Тогда из (5.9) получаем
wmax = [2k/(k – 1) p1v1]1/2 м/с,
а для идеального газа (pv = RT) wmax = [2k/(k – 1) RT1]1/2 м/с.
Здесь можно говорить о том, что внутренняя энергия газа полностью превращается в кинетическую энергию поступательного движения (хаос перешел в упорядоченность).
Процесс течения газа в сопле Лаваля можно показать на диаграммах p – v и h – s (см.
рис. 2.33).
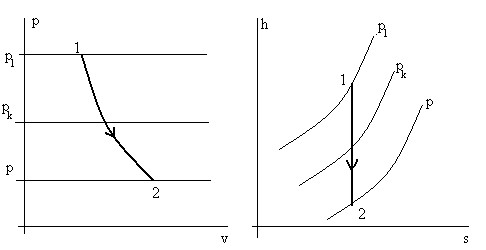
Рис. 2.33. Процесс течения газов в сопле Лаваля в координатах p – v и h – s при 0 < β < βk.
Найдем скорость потока в критическом сечении канала, т.е. там, где устанавливается максимальный расход и где
β = βk = [2/(k + 1)]k/(k – 1).
Согласно формуле w = [2k/(k – 1) p1v1(1 – β(k – 1)/k)]1/2 имеем:
wk = [2/(k – 1) p1v1 (1 – βk(k – 1)/k)]1/2 = [2/(k – 1) p1v1(1 – 2/(k + 1))]1/2 = [2k/(k + 1)
p1v1]1/2
Эту же скорость можно вычислить и по формуле w = (2(h1 – h))1/2:
Wk = [2(h1 – hk)]1/2
Каков физический смысл критической скорости и явлений в этом состоянии? Из формулы β = βк = (2/(k – 1))k/(k – 1) имеем:
βk = pk/p1 = (2/(k + 1))k/(k – 1) → 2/(k + 1) = (pk/p1)(k – 1)/k = pk/p1 (p1/pk)1/k.
Далее, в формуле (5.13) можно увидеть, что
2k/(k + 1) =[2/(k + 1)] k.
Отсюда: wk = [pk/p1 (p1/pk)1/k kp1v1]1/2 → (p1/pk)1/k = vk/v1 → wk = [kpkvk]1/2 = ak.
Таким образом, математически строго показали, что критическая скорость равна скорости звука, и это происходит в минимальном сечении сопла Лаваля. Следовательно, скорость течения в канале тесно связана со свойствами рабочего тела (движущегося вещества). Естественно, что подобная связь процесса движения в канале со свойствами вещества отражается на характере продвижения потока в канале.
Из уравнения сплошности ρw = G/F при F = Fmin плотность потока массы ρw кг/м2с максимальна, достигнут предел сжимаемости – больше канал в принципе пропустить не может. Аналогия - бегство толпы людей со стадиона через узкие ворота. При панике эти ворота не пропустят больше плотно бегущих людей, как бы задние ряды не нажимали на первые ряды двигающихся людей.
Пример 1. Для вспрыскивания солярки (топлива) в цилиндры дизельного двигателя используется сопло Лаваля (инжектор). Давление воздуха в цилиндре двигателя в конце такта сжатия р = р2 = 5,0 бар. Воздух подается в инжектор от компрессора при давлении р1 = 12 бар и температуре Т1 = 610К. Определить скорость воздуха на выходе из сопла Лаваля.
Решение. 1-ый способ. Чтобы решить, какой расчетной формулой следует пользоваться для определения скорости воздуха, необходимо прежде всего определить тип течения: дозвуковой, звуковой или сверхзвуковой на выходе из сопла. Для этого надо найти величину β и сравнить ее с βk. β = p2/p1 = 5/12 = 0,417. βk = (2/(k + 1))k/(k – 1).
Следовательно, для расчета βk необходимо найти k = cp/cv. По таблицам теплоемкостей для воздуха находим истинные мольные теплоемкости при Т1 = 610К = 3370С:
μср(t = 3370C) = 30,266 кДж/кмольК. μсv(t = 3370C) = 21,951 кДж/кмольК.
Отсюда k = μcp/μcv = 30,266/21,951 = 1,3788 ≈ 1,4. βk = (2/(1,4 + 1))1,4/(1,4 – 1) = 0,528.
Получилось, что β = 0,417 < βk = 0,528. Рассмотрим рис. 2.34. Из него следует, что перепад давлений таков, что произойдет полное расширение воздуха в сопле Лаваля от р1 = 12 бар до р2 = 5 бар.
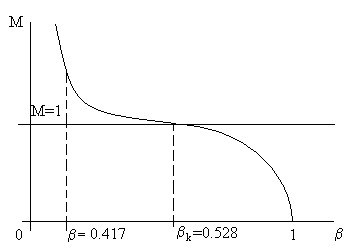
Рис. 2.34. Иллюстрация к примеру 1. Здесь видно, что течение на выходе из cопла – сверхзвуковое (М > 1).
Процесс течения в диаграмме p- v и T – s показан на рис. 3.35.
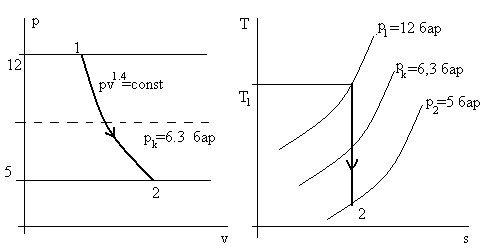
Рис. 2.35. Изображение процесса течения воздуха в сопле Лаваля для примера 1. Здесь рk = p1βk = 12*0,528 = 6,3 бара.
Для получения ответа задачи воспользуемся формулой w = [2k/(k – 1) p1v1(1 – β(k – 1)/k)]1/2, уже точно зная, что в нее следует подставлять величину β = 0,417, а не βk = 0,528, так как в сопле происходит полное расширение воздуха.
w = [2k/(k – 1) p1v1 (1 – β(k – 1)/k]1/2 → pv = RT → w = [2k/(k – 1) RT1 (1 – β(k – 1)/k]1/2 =
[2*1,4/(1,4 – 1)*(8314/29)*610*(1 – 0,417(1,4 – 1)/1,4)]1/2 = 520 м/с.
Решение. 2-ой способ. Опять, как и в первом способе решения задачи, определим, что происходит полное расширение воздуха от р1 = 12 бар до р2 = 5 бар. В качестве расчетной формулы для определения скорости истечения из сопла возьмем теперь (5.10). Следовательно, надо найти h1 – h2 = Δh. Здесь поступаем просто:
Δh = cpm|t2t1*Δt,
Где Δt = T2 – T1 = t2 – t1. Но температура воздуха во второй точке процесса пока не известна. Найдем ее:
T2/T1 = (p2/p1)(k – 1)/k → T2 = T1(p2/p1)(k – 1)/k = 610(5/12)(1,4 – 1)/1,4 = 475K = 2020C.
По таблицам теплоемкостей для воздуха ищем среднюю массовую изобарную теплоемкость (см. семинар по теплоемкости)
cpm|337202 = (cpm|3370 *337 - cpm|2020 *202)/(337 – 202) = (1,0191*337 – 1,0115*202)/(337 – 202) = 1,0302 кДж/кг К.
Далее, Δh = cpm|337202*Δt = 1,0302*(337 – 202) = 139 кДж/кг.
w = [2*Δh]1/2 = [2*139*103]1/2 = 527 м/с.
Ответ: скорость истечения из сопла 520 м/с.
Пример 2. Ручным насосом производится подкачка автомобильной шины, давление в которой р2 = 2 бара, а в насосе создается давление р1 = 5 бар и температура при этом t1 =
470C. Определить давление на выходе из насоса и время процесса подкачки, считая условно неизменной скорость истечения из насоса с отверстием диаметром d = 5мм. Объем подкачки V = 50 литров.
Решение. Прежде всего, приведем все исходные данные в систему СИ: Т1 = 47 + 273 = 320К, d = 5*10-3 м, V = 50*10-3 м3.
Определяем характер истечения – дозвуковой, звуковой или сверхзвуковой. Сразу можно сказать, что сверхзвукового течения в принципе быть не может, так как канал не профилирован как сопло Лаваля (в тексте задачи об этом ничего не сказано). Рассчитаем степень расширения β = р2/р1 = 2/5 = 0,4 < βk ≈ 0,5.
Из теории, изложенной выше, известно, что в не профилированном отверстии достигается только критическая (звуковая) скорость течения. Следовательно, на выходе из отверстия насоса все параметры состояния воздуха – критические.
Давление на выходе из отверстия: рk = βk*p1 = 0,5*5 = 2,5 бара. Температура в критическом (выходном) сечении:
Тk = T1*(pk/p1)k/(k-1) = 320*0,51,4/(1,4 – 1) = 269K = - 40C.
Удельный объем воздуха в критическом состоянии: vk = RTk/pk =
8314*269/(29*2,5*105) = 0,309 м3/кг.
Скорость истечения (это скорость звука):
wk = [k*pk*vk]1/2 = [1,4*2,5*105*0,309]1/2 = 328 м/с.
Объемный расход воздуха из насоса в камеру автоколеса:
Vk = F*wk = 0,785*d2*wk = 0,785*(5*10-3)2*328 = 3,22*10-2 м3/с.
Время подкачки одной автошины:
τ = V/Vk = 50*10-3/3,22*10-2 = 1,55 с.
Ответ: давление на выходе из насоса pk = 2,5 бара; время подкачки τ = 1,55 с.
Замечание к примеру 2. Расчетный режим истечения сжатого воздуха из отверстия и далее по патрубку в камеру получился критический. Полный перепад давления р1 – р2 = 5 – 2 = 3 бара не используется для технической цели. Энергия давления (а это потенциальная энергия газа) пропадает, тратится на трение, на перестройку профиля скорости, диссипирует (рассеивается).
На рис. 2.36 представлены диаграммы p – v и h – s для процесса во втором примере.
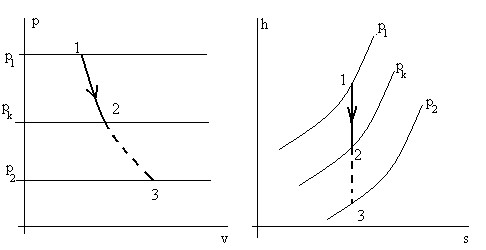
Рис. 2.36. Процесс истечения в примере 2.
Пунктиром показан процесс полного расширения 1 – 3 воздуха, если бы использовалось сопло Лаваля.
Замечание. При истечении через отверстие (сверление), патрубок, штуцер поток сам формирует сужающуюся струю (см. пунктир на рис. 2.37), и при этом часть кинетической энергии потока расходуется на подобную перестройку.
Рис. 2.37. Самоорганизация струи (потока) при течении через отверстие.
Более того, образуются вихри, которые подвержены силам трения о стенку. На поддержание движения этих вихрей тоже тратится энергия потока.
Для снижения этих потерь (а эти потери – это в конце концов рост себестоимости продукта химической технологии) в машинах и аппаратах перед сечением с критической (звуковой) скоростью устанавливают конфузор, а за отверстием – диффузор с углом раскрытия конуса ≈ 80 - 120.
Пример 3. Водяной пар с параметрами р1 = 12 бар и температурой Т1 = 610К используется в качестве рабочего тела в инжекторе, входная часть которого имеет форму сужающегося конуса (конфузора). Найти давление и скорость истечения из конфузора в среду с давлением р2 = 5 бар.
Решение. Водяной пар относится к категории реальных газов, определение его параметров состояния производится по фазовым диаграммам или по таблицам. Проведем решение задачи с использованием диаграммы h – s для водяного пара (см. рис. 2.38).
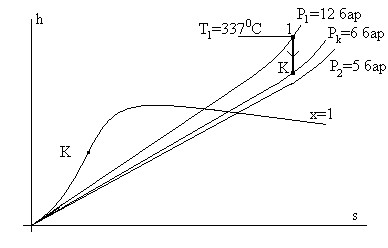
Рис. 2.38. Иллюстрация к решению задачи примера 3. Диаграмма состояния h – s и ход процесса течения пара в конфузоре.
Сначала, как всегда, определяем характер истечения струи: дозвуковой, звуковой или сверхзвуковой. Так как конфузор не является соплом Лаваля, то сверхзвукового течения в принципе быть не может.
Величина β = р2/р1 = 5/12 = 0,42, а βk ≈ 0,5 для водяного пара. Следовательно, β < βk и в соответствии с изложенной теорией течение пара на выходе из конфузора будет критическим (звуковым). В частности, давление пара будет равно рk = βk*p1 = 0,5*12 = 6 бар.
Теперь находим параметры состояния в точке 1 и точке «К» (см. рис. 5.13). Точка 1 находится как пересечение изобары р1 = 12 бар с изотермой Т1 = 610К = 3370С. Для этой же точки 1 (она оказалась в области перегретого пара) находим по диаграмме энтальпию h1 = 3128 кДж/кг. Точка К находится на пересечении изобары рk = 6 бар и изоэнтропы из точки 1. Здесь же сразу находим hk = 2944 кДж/кг. Точка К оказалась тоже в области перегретого пара.
Используя формулу du + d(w2/2) = δq – δlпотока – δlтрения, получаем:
w = wk = [2*(h1 – hk)]1/2 = [2*(3128 – 2944)*103]1/2 = 607 м/с.
Ответ: давление на срезе конфузора рk = 6 бар, скорость истечения wk = 607 м/с.
Вопрос. Поместим девушку – студентку в область перед конфузором (см. предыдущий пример), а юношу – студента в область за конфузором. Пусть юноша громко приглашает девушку в кино. Будет ли реализовано его приглашение?
Рассмотренное выше движение газа (пара) по каналам различной формы происходило в условиях адиабатно-изоэнтропийного процесса. Это возможно в идеальных условиях отсутствия трения и теплообмена с внешней средой. В реальных течениях поток взаимодействует со стенкой канала, а высокая температура потока неизбежно ведет к теплопередаче с окружающей средой.
Последнее обстоятельство является предметом специального курса «Теплообмен», в рамках дисциплины «Процессы и аппараты химической технологии», и мы его касаться не будем.
Трение возникает по причине шероховатости внутренней поверхности канала и вязкости рабочего тела (свойство вещества). При движении по каналу в месте контакта с поверхностью поток полностью теряет скорость (w = 0), возникает профиль скорости по радиусу канала с максимумом на оси симметрии канала. В термодинамике такие детали не рассматриваются, а скорость потока принимается постоянной по радиусу и равной
w = 4Gv/πd2 м/с,
где G – массовый расход среды кг/с, d – диаметр канала в данном сечении, м. И вся
работа трения условно сносится на поверхность контакта потока со стенкой канала. Тогда схема термодинамической системы для реальных течений сводится к взаимодействию потока с окружающей средой, т.е. стенкой канала + атмосферой.
Для неподвижного канала (δlтехнич = 0) применимо уравнение du + d(w2/2) = δq – δlпотока
– δlтрен + δlтехн
Напомним, что работа трения полностью диссипирует, т.е. обращается в тепловую энергию, которую поток (а он не различает причину) воспринимает как подвод теплоты из окружающей среды: lтрения = qтрения.
Уравнение энергии потока без учета теплообмена получает следующий вид:
dw2/2 + dh + δlтрения = 0
и, если считать начальную скорость потока (на входе в канал) нулевой, то получаем
w = [2(h1 – hтрения)]1/2
В этой формуле величина энтальпии hтрения рассчитывается по эмпирическим данным следующим образом:
hтрения = hs + Δтрения
где hs – величина энтальпии в конечной точке идеального процесса течения при s =
const, а Δтрения – потери энтальпии на работу трения. Эта величина рассчитывается как
Δтрения = w2/2 (1 – φ2) = (h1 – h2)(1 – φ2)
Здесь φ – коэффициент скорости, φ ≡ wтрения/ws, является опытной или справочной величиной для данного канала.
Рассмотрим рис 3.39, на котором изображена диаграмма h – s и процесс течения с трением.
![]() Дросселирование
Дросселирование
– процесс 1-4 h=const
Рис. 2.39. Иллюстрация к расчету скорости в канале с учетом трения.
Из рис. 2.39 следует, что точка 3 находится на изобаре р2 = const и она расположена правее точки 2 согласно 2 – му закону термодинамики (Δsдиссип = s3 – s2 > 0).
При встрече потока с сужением (вентиль, капилляр, мембрана с малым отверстием на оси и т.п.) потери на трение максимальны. Работа трения переходит в теплоту и вся эта теплота остается в потоке. Поэтому такой процесс (его называют дросселированием или мятием) имеет инвариант h = const. Наверное, понятно из рис. 2.39 (см. процесс 1 – 4 (пунктир)), что при дросселировании давление уменьшается (dp < 0), удельный объем вещества в потоке соответственно растет (dv > 0), энтропия обязательно увеличивается (ds > 0).
Пример 4. Пар движется по конфузору в условиях примера 3, но с трением при известном коэффициенте скорости φ = 0,93. Найти реальную скорость пара на выходе из конфузора. Решение. Потери энтальпии на трение рассчитываются по формуле:
Δтрения = (h1 – hk)(1 – φ2) = (3128 – 2944)(1 – 0,932) = 25 кДж/кг.
Величина энтальпии пара на выходе из конфузора (точка 3 на рис. 2.39) равна:
hтрения = hk + Δтрения = 2944 + 25 = 2969 кДж/кг.
Реальная скорость истечения пара из конфузора:
w3 = [2(3128 – 2969)103]1/2 = 564 м/с (а было w2 = 607 м/с).
Ответ: скорость истечения пара из конфузора w3 = 564 м/с.
Пример 5. В цехе химического завода со взрывоопасными условиями работы приводом для компрессора является паровая турбина с питанием перегретым паром с давлением р = 5 бар, а заводская котельная производит пар с давлением 15 бар и температурой 2400С. Как трансформировать котельный пар и сделать его пригодным для паровой турбины?
Решение. Один из способов трансформации (не единственный) – подвергнуть пар из котельной мятию (дросселированию) (см. рис. 2.39, процесс 1 – 4).
По диаграмме h – s для водяного пара находим параметры состояния в точке 1. Сама точка 1 находится на пересечении изобары р1 = 15 бар и изотермы Т1 = 2400С. Считываем с диаграммы для точки 1 величину энтальпии h1 = 2898 кДж/кг.
Точка 4 (см. рис. 2.39) находится на пересечении линии h = const = 2898 кДж/кг и изобары р2 = 5 бар. Опять с диаграммы считываем величину температуры Т2 = 2250С.
Ответ: можно применить процесс дросселирования до давления р2 = 5 бар. Получится перегретый пар, пригодный для питания турбины.
Замечание. Конечно, такое решение проблемы обрадует заводчан своей простотой и отсутствием специальной обслуги «трансформации» пара. Но решение очень не экономичное: из хорошего и дорогого пара сделали пар с большой энтропией, себестоимость целевого продукта химического завода такое решение только увеличит.
Основное предназначение теплосиловых установок – это превращение теплоты в работу. Термодинамика не запрещает такое превращение, так как согласно первому закону термодинамики:
du = dq – dw → dw = dq – du
Следовательно, получать работу dw > 0 можно или/и подводом теплоты dq > 0 или/и уменьшением внутренней энергии du < 0.
В химической технологии и энергетике теплосиловые установки применяются как источники энергии для компрессоров, вакуум-насосов, вентиляторов и газодувок, насосов для перемещения жидкостей, для приведения в действие дробилок и других измельчителей. В энергетике теплосиловые установки используют для производства электроэнергии и теплоты для обогрева.
Эти двигатели различают по виду топлива на бензиновые и дизельные. На рис. 2.40 представлена индикаторная диаграмма цикла бензинового двигателя.
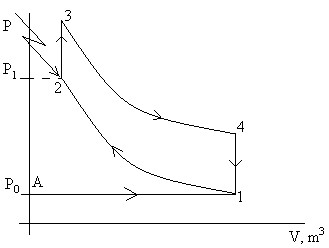
Рис. 2.40. Индикаторная диаграмма бензинового двигателя внутреннего сгорания. А1 – процесс всасывания паро-воздушной смеси в объем цилиндра;
1 – 2 – сжатие этой смеси; в точке 2 возбуждение искры запального устройства (свечи);
2 – 3 – вспышка (взрыв) паров бензина в смеси с кислородом воздуха;
3 – 4 – процесс политропического расширения дымовых газов;
в точке 4 – открытие выхлопного клапана;
4 – 1 процесс выхлопа дымовых газов в атмосферу.
На рис. 2.41 представлена индикаторная диаграмма дизельного двигателя внутреннего сгорания.
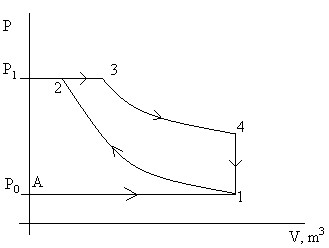
Рис. 2.41. Индикаторная диаграмма дизельного двигателя внутреннего сгорания.
А1 – процесс всасывания чистого воздуха из атмосферы в цилиндр двигателя;
1 – 2 – процесс сжатия воздуха; в точке 2 – впрыск дизельного топлива в цилиндр;
2 – 3 – горение топлива; 3 – 4 –процесс политропического расширения;
т. 4 – открытие выхлопного клапана; 4 – 1 – выхлоп дымовых газов в атмосферу.
Можно показать, что термический коэффициент полезного действия ηt двигателей внутреннего сгорания сильно зависит от степени сжатия р1/р2: чем больше эта степень, тем больше ηt. Для бензинового двигателя степень сжатия ограничена температурой самопроизвольной вспышки паров бензина в смеси с кислородом воздуха. Поэтому паровоздушную смесь приходится сжимать до температуры ниже температуры вспышки, а само горение (взрывного типа) инициируют с помощью искры в запальной свече.
В дизельных двигателях сжимается чистый воздух, степень сжатия в таких двигателях ограничена только прочностными свойствами материалов для изготовления двигателей. Поэтому степень сжатия в дизельном двигателе много больше степени сжатия в бензиновом двигателе и, соответственно, ηt – тоже.
Для бензиновых двигателей η ≈ 25% – 30%, для дизельных η ≈ 40% - 45%. Это значит, что из 10 литров бензина в баке на собственно движение автомобиля будет израсходовано только 2,5 литра, а остальное пойдет на обогрев атмосферы и экологическую грязь. Зато у дизельного двигателя чуть меньше половины топлива будет истрачено с пользой, а остальное – потери.
На рис. 2.42 представлена технологическая схема паросиловой установки для производства электроэнергии.
Пар большого давления и температуры подается в сопловые аппараты турбины, где происходит превращение потенциальной энергии пара в кинетическую энергию потока пара (скорость потока – сверхзвуковая). Кинетическая энергия сверхзвукового потока превращается на лопатках турбины в кинетическую энергию вращения колеса турбины и в работу производства электроэнергии.
На рис. 2.42 показана одна турбина, на самом деле турбина имеет несколько ступеней расширения пара.
После турбины пар направляется в конденсатор. Это обычный теплообменник, внутри труб проходит охлаждающая вода, снаружи – водяной пар, который конденсируется, вода становится жидкой.
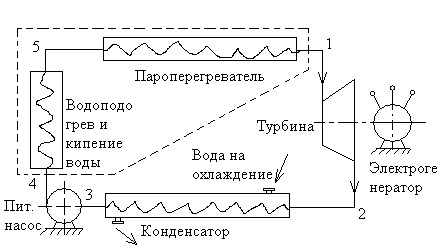
Рис. 2.42. Принципиальная технологическая схема паросиловой установки.
Эта вода поступает в питательный насос, где происходит увеличение давления до номинальной (проектной) величины.
Далее вода с высоким давлением направляется в котельный агрегат (на рис. 2.42 он обведен штриховой линией). В этом агрегате вода сначала нагревается до температуры кипения от дымовых газов из топки котла, затем поступает в кипятильные трубы, где происходит фазовое превращение вплоть до состояния сухого насыщенного пара (см. т. 5 на рис.
2.42).
Наконец, сухой насыщенный пар идет в пароперегреватель, обогреваемый топочными дымовыми газами из топки. Состояние пара на выходе из пароперегревателя характеризуется точкой 1. Так замыкается цикл. Этот цикл паросиловой установки предложил немецкий инженер Ренкин[22], и потому его и назвали циклом Ренкина..
Рассмотрим цикл Ренкина на трех термодинамических диаграммах p – v, T – s, h – s (см. рис. 2.43).
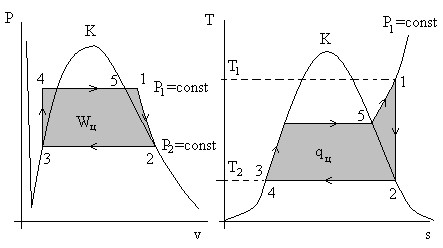
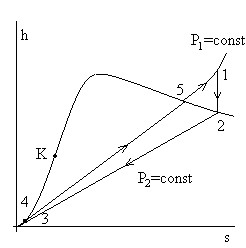
Рис. 2.43. Цикл Ренкина на термодинамических диаграммах. Нумерация точек совпадает с нумерацией на рис. 6.3.
Процесс 1 – 2 – расширение пара в соплах турбины;
2 – 3 – процесс конденсации пара; 3 – 4 – процесс в питательном насосе; 4 – 5 – процесс нагрева воды и ее кипение; 5 – 1 – процесс перегрева пара. Заштрихованы те области диаграмм, площадь которых численно равна работе и теплоте за цикл, причем qц = wц.
Из технологической схемы на рис. 2.42 и диаграммы Т – s на рис. 2.43 следует, что теплота подводится к рабочему телу в процессах 4 – 5 – 1, у которых ds > 0. И эти процессы характеризуются инвариантом p1 = const. Поэтому подводимая в цикле Ренкина теплота qподв равна:
qподв = h1 – h4. Дж
Теплота отводится от рабочего тела в процессе 2 – 3 (ds < 0) и этот процесс тоже p2 = const. Поэтому
qотв = h2 – h3. Дж
Разность между подведенной теплотой и отведенной представляет собой теплоту цикла qц, превращенную в работу wц
wц = qц = (h1 – h4) – (h2 – h3) = (h1 – h2) – (h4 – h3).
Разность энтальпии воды до питательного насоса (точка 3) и после (точка 4) ничтожно мала. В связи с этим
wц = qц = h1 – h2
Термический коэффициент полезного действия цикла Ренкина (а это отношение «пользы», т.е. wц, к «затратам», т.е qподв) равен
ηt = (h1 – h2)/(h1 – h4)
Пример. Паросиловая установка работает по циклу Ренкина с начальными параметрами пара р1 = 20 бар и t1 = 3000С. Давление в конденсаторе р2 = 0,05 бара. Найти термический коэффициент полезного действия ηt.
Решение. Как следует из общего метода решения задач, в которых фигурирует реальное рабочее тело, прежде всего необходимо выяснить состояние воды в первой точке цикла (см. рис. 2.43), чтобы знать, какими таблицами для водяного пара следует пользоваться для поиска необходимых параметров.
По таблицам насыщенных паров для Н2О по величине р1 = 20 бар находим температуру насыщения (кипения): tн = 2120С. Сравниваем эту величину с t1 = 3000C. Так как t1 > tн, то делаем вывод: в точке 1 водяной пар находится в перегретом состоянии и, следовательно, необходимо пользоваться таблицей для перегретого водяного пара. Глядя на (6.5), видно, что для решения задачи из таблицы необходима энтальпия в точке 1: h1 = 3019 кДж/кг.
Далее переходим к определению параметров состояния пара в точке 2. Про эту точку знаем, что р2 = 0,05 бара и что s2 = s1= 6.757 кДж/кгК (здесь мы мысленно провели изоэнтропу из точки 1 до изобары р2 = const, так как процесс 1 – 2 – это процесс истечения пара в соплах турбины).
Снова традиционно обращаемся к таблице насыщенного водяного пара по давлениям и видим, что при р2 = 0,05 бара энтропия s΄ = 0,4761 кДж/кгК для кипящей воды и энтропия s” = 8,393 кДж/кгК для сухого насыщенного пара. Сравнивая величины энтропий s΄, s” и s2, видно, что точка 2 находится в области влажного (насыщенного) пара и, следовательно, придется пользоваться таблицами влажного водяного пара.
Глядя на ηt = (h1 – h2)/(h1 – h4), видно, что для решения задачи необходимо определить величину энтальпии в точке 2. Для этого придется сначала найти степень сухости водяного пара в точке 2, и только потом определим h2.
s2 = s1 = s΄ + xr/Tн → x = (s1 - s΄)Tн/r.
Теплоту фазового перехода воды при давлении р2 = 0,05 бара находим по тем же таблицам насыщенного водяного пара: r = 2423 Кдж/кг. Здесь же находим температуру пара в точке 2: t2 = tн = 32,880С. Тогда
x = (6,757 – 0,476)(32,88 + 273)/2423 = 0,793.
Теперь можно рассчитать энтальпию водяного пара в точке 2:
h2 = h΄ + xr → h2 = 137,83 + 0,793*2423 = 2059 кДж/кг.
Величину энтальпии кипящей воды h΄ = 137,83 кДж/кг = h4 опять-таки находим по тем же таблицам насыщенного водяного пара. Окончательно:
ηt = (см. (6.5)) = (3019 – 2059)/(3019 – 137,83) = 0,333.
Ответ: ηt = 0,333 = 33,3%.
Замечание. Такая величина термического коэффициента полезного действия по существу означает следующее. Из 100 вагонов угля, сжигаемого в топке котельного агрегата, добытого где-то в Кузбассе тяжким и опасным трудом шахтеров, привезенных, скажем, на Кольский полуостров в город Кировск по железной дороге, - только 34 вагона угля будут «превращены» в электроэнергию, а остальные 66 вагонов пойдут на обогрев атмосферы. Какое расточительство!
Горячая вода из конденсаторов некоторых ТЭЦ на берегах р. Москвы сбрасывается в реку. Дикие утки не хотят лететь на зиму в Африку, им и у ТЭЦ хорошо, а для нас это разорение.
Замечание. Найдем термический коэффициент полезного действия цикла Карно в тех же температурных пределах, что и в рассмотренном примере. Температуру воды в конденсаторе уже определили по таблице насыщенного водяного пара при р2 = 0,05 бара:
tн = 32,880С.
ηкt = 1 – T2/T1 = 1 - (32,88 + 273)/(300 + 273) = 0,466 = 46,6%
Иными словами, самый совершенный цикл, т.е. цикл Карно, имеет КПД в условиях задачи рассматриваемого примера чуть меньше половины (из 100 вагонов угля половина уйдет на обогрев атмосферы). И здесь с термодинамикой спорить бесполезно.
Рис. 2.44 демонстрирует причину малого КПД цикла Ренкина по сравнению с циклом Карно.
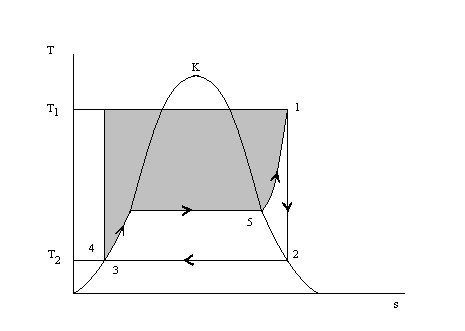
Рис. 2.44. Иллюстрация причины малого КПД цикла Ренкина по сравнению с циклом Карно. Потери работы – заштрихованная площадь.
Замечание. Совершенство паросиловой установки определяется не только термическим коэффициентом полезного действия цикла, но и коэффициентом полезного действия котельного агрегата. Последний представляет собой отношение подведенной теплоты к рабочему телу к химической энергии топлива. К чести отечественных теплоэнергетиков, разработчиков котельных агрегатов КПД современной котельной установки составляет величину 99,5%. Это значит, что из 100 вагонов угля 99,5 вагонов угля будут «превращены» в энтальпию перегретого пара (точка 1 на рис. 6.3, 6.4 и 6.5) и только 0,5 вагона угля уйдут на обогрев атмосферы. Следовательно, низкий КПД всей паросиловой установки, работающей по циклу Ренкина, имеет глубокие термодинамические (генетические) основания.
Суть этих оснований в том, что природа воды, ее физико-химические свойства таковы, что цикл Ренкина слабо заполняет площадь внутри цикла Карно (см. рис. 6.5).
Воду сделали рабочим телом в паросиловых установках чисто исторически довольно давно. А причина этого в том, что вода – самое распространенное вещество на Земле, воды раньше было много, она была бесценна. Сегодня малая стоимость воды стала мифом: вопервых, воды что-то стало мало, промышленность России давно сидит на голодном пайке; во-вторых, вода из реки, озера, водохранилища или артезианской скважины оказалась просто непригодной, в ней много примесей, солей жесткости, растворенных газов, все это сильно уменьшает надежность и котельного агрегата, и турбины. Современная обработка воды для паросиловой установки делает ее очень дорогой. Даже воду для охлаждения конденсатора приходится тщательно очищать от водорослей, амеб, жгутиковых организмов, микроорганизмов, так как они великолепно живут и активно размножаются в теплообменнике, приводя всю установку в состояние отказа.
Коэффициенты полезного действия и двигателей внутреннего сгорания и паросиловых установок – расточительно малы. Следовательно, приходится и/или разрабатывать мероприятия по увеличению КПД и/или заниматься энергосбережением.
Прежде чем перейти к описанию термодинамических методов и приемов по увеличению КПД, введем некоторое вспомогательное понятие. Необходимость этого введения состоит в следующем. Дело в том, что ηt, по определению, есть отношение «пользы» к «затратам». Практически все методы повышения КПД одновременно изменяют и числитель и знаменатель дроби ηt. И поэтому возникает неопределенность в поведении всей дроби.
С другой стороны, этой неопределенности нет, если имеем дело с циклом Карно, так как изменение температуры источника теплоты Т1 и стока теплоты Т2 довольно однозначно говорит об изменении ηtк. Кроме того, все термодинамические методы и приемы повышения КПД паросиловых установок не изменяют величину Т2, так как практически ее трудно изменить.
Итак, подвод теплоты в цикле Ренкина происходит по некоторой ломаной кривой
(см. рис. 6.4 и диаграмму Т – s, процесс 4 – 5 – 1, р1 = const).
Определение: средне интегральной температурой процесса подвода теплоты в паросиловом цикле называется
![]() Tds (6.6)
Tds (6.6)
Иными словами, <Т1> в математике называют средне интегральной величиной функции на каком-то интервале изменения аргумента. Тогда для любого цикла паросиловой установки эквивалентный цикл Карно будет иметь КПД, равный:
ηtк = 1 – Т2/<T1>
Любое предложение по увеличению или изменению ηt паросиловой установки будем оценивать по изменению <T1>.
1. Повышение температуры рабочего тела перед турбиной.
На рис. 2.45 представлена иллюстрация этого приема повышения термического коэффициента полезного действия.
Обращаем внимание, что количество «пользы», т.е. работы за цикл увеличилось с увеличением Т1, но одновременно увеличились потери теплоты в конденсаторе, увеличились затраты теплоты за цикл. Здесь наглядно видно, что у дроби ηt увеличился и числитель и знаменатель, а результат неопределенен (см. (6.5)). Зато воочию видно, что увеличение Т1 до Т1΄ увеличивает <T1>. Следовательно, ηt увеличивается с увеличением Т1.
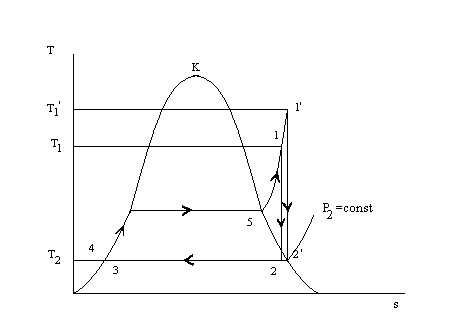
Рис. 2.45. Иллюстрация метода повышения ηt путем увеличения температуры Т1 пара перед турбиной.
Замечание. Производя увеличение Т1, мы сознательно не меняли все остальные параметры цикла Ренкина. Нельзя же изменять все сразу, чтобы выявить какую-то закономерность.
2. Повышение давления рабочего тела перед турбиной.
На рис. 2.46 представлена иллюстрация этого метода повышения ηt.
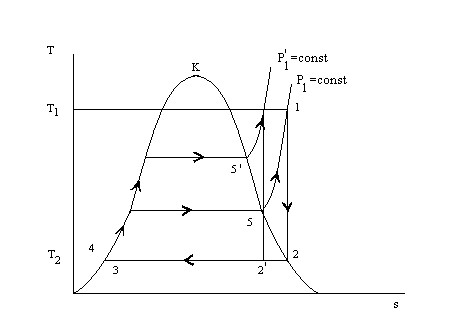
Рис. 2.46. Иллюстрация метода повышения ηt путем повышения давления водяного пара перед турбиной.
Судя по рис. 2.46, трудно решить, увеличились или уменьшилась работа за цикл, зато потери теплоты в конденсаторе явно уменьшились. Если же использовать понятие <T1>, то из рис. 2.46 следует, что с увеличением р1 величина <T1> тоже увеличилась, а температура Т2 не изменилась. Следовательно, однозначно можно сделать вывод, что увеличение давления пара перед турбиной увеличивает термический коэффициент полезного действия ηt.
Замечание. Повышение температуры Т1 пара перед турбиной мало эффективно, так как изобары p = const довольно круто идут вверх в области перегретого водяного пара. Такова уж природа этого вещества.
Оба метода повышения ηt, показанных выше, «благославляются» термодинамикой. А практически увеличение температуры и давления водяного пара перед турбиной ограничивается набором термостойких и особо прочных материалов для изготовления и котельного агрегата и турбины. Здесь во весь свой грозный рост встает наука «Материаловедение».
3. Многократный перегрев пара.
Суть этого метода повышения КПД теплосиловой установки состоит в следующем. Турбина, как правило, имеет несколько ступеней расширения пара. Это позволяет водяной пар после первой ступени расширения снова направить в свой пароперегреватель, расположенный в газоходах котельного агрегата. Ничто не мешает сделать тоже самое с паром после второй ступени расширения и т.д. На практике делают не больше трех промежуточных перегревов, так как установка сильно усложняется, увеличивается число и длина паропроводов, запорной и регулирующей арматуры. Все это уменьшает надежность паросиловой установки.
На рис. 2.47 представлена иллюстрация метода повторного перегрева водяного пара для увеличения термического коэффициента полезного действия паросиловой установки.
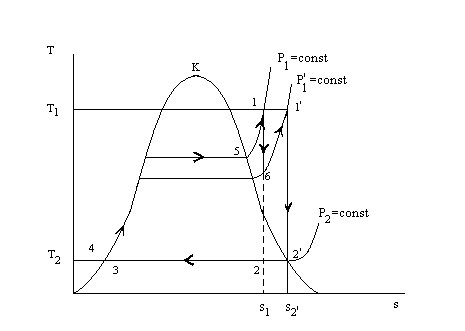
Рис. 2.47. Иллюстрация метода повышения ηt путем двойного перегрева водяного пара. Процесс 5 – 1 – первый перегрев перед первой ступенью турбины, процесс 6 - 1΄ - второй перегрев перед второй ступенью турбины.
Замечание. Термодинамика рекомендует уменьшать давление р2 в конденсаторе с целью уменьшения температуры Т2. Это предложение трудно реализуемо, т.к. охлаждение пара осуществляется посредством проточной воды с температурой в окружающей среде. Это значит, что летом при температуре воды на охлаждение t = 250С давление конденсации (кипения) равно р2 = 0,03166 бара (см. таблицы насыщенного водяного пара по температурам). Зимой при t = 0,010C давление конденсации равно р2 = 0,006108 бар. И сделать ниже этой величины невозможно (вода становится льдом).
Конечно, можно поставить холодильную машину для проведения процесса конденсации с целью уменьшения Т2, но прирост работы за цикл wц не перекрывает затрат работы в холодильной установке.
Окончательно, как следует из опыта и практики повышения ηt паросиловых установок указанными методами, сделать термический коэффициент полезного действия больше
40% - 42% не удается.
4. Теплофикация.
Суть метода теплофикации заключается в том, чтобы потери теплоты в цикле Ренкина (в конденсаторе) сделать «пользой». Организация процесса теплофикации заключается в следующем (см. рис. 2.48).
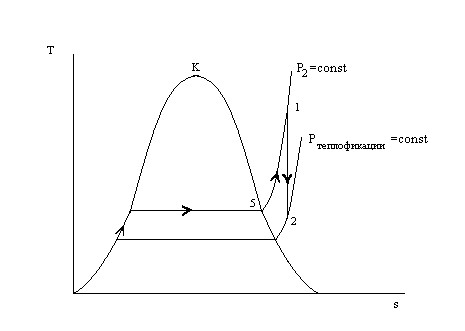
Рис. 2.48. Иллюстрация к объяснению процесса теплофикации.
Водяной пар с состоянием т. 1 направляется в паровую турбину, но процесс расширения проводится не до конца, а до давления ртеплофик. Далее, пар после турбины направляется по паропроводу в тепловые пункты жилых районов. В этих пунктах установлен теплообменник, который нагревает питьевую воду из водопроводной сети за счет процесса конденсации пара из паропровода. Часть горячей воды идет на отопление жилых и производственных зданий, другая часть – на бытовые нужды. Конденсат возвращается обратно в паросиловую установку на вход питательного насоса.
Идея этого метода состоит в том, что «пользой» для паросиловой установки теперь является не только работа турбины, но и теплота перегретого пара, направляемая в жилые районы. И жители города, промышленные предприятия платят поставщикам тепловой энергии.
Теплофикация получила самое широкое распространение в России, так как Россия все-таки северная страна с суровым климатом.
5. Двойные циклы.
Глядя на рис. 2.44, очень хочется в заштрихованной области цикла Карно расположить еще один цикл с каким-то другим рабочим телом так, чтобы процесс 4 – 5 – 1 паросилового цикла играл роль стока теплоты для первого цикла. Это и есть идея двойного цикла: максимально приблизиться к циклу Карно. Сначала попробовали использовать ртуть в качестве рабочего тела, но пришлось отказаться из-за опасных свойств этого вещества.
В настоящее время идет активная разработка паро-газового цикла. Суть его состоит в следующем. В специальной топке при высоком давлении сжигается жидкое или газообразное топливо. Дымовые газы направляются в газовую турбину, на валу которой устанавливается центробежный компрессор для сжатия воздуха, подаваемого в топку, и электрогенератор для получения электроэнергии. Все еще очень горячие дымовые газы после газовой турбины далее становятся источником теплоты для паросиловой установки, работающей на воде.
Коэффициент полезного действия такой установки в действующем пилотном варианте достигает 80%, а это уже большая победа. Увеличение коэффициента полезного действия достигается за счет двух обстоятельств. Во-первых, цикл паро-газовой установки приближен к циклу Карно. Во-вторых, увеличена температура источника теплоты Т1.
Реализация такого цикла облегчается тем, что в России существует промышленный опыт создания турбо-винтовых двигателей для авиации.
Люди довольно давно поняли расточительность теплосиловых установок и осознали необходимость рачительного использования каждого полученного кДж энергии.
Оказывается, энергосбережение возможно на государственном уровне, хотя апологеты рыночной экономики (читай: капитализма) утверждают, что рынок сам решит все проблемы и энергетические тоже. Прелагаем примеры энергосбережения на государственном уровне.
Известно, что лампочка накаливания имеет КПД, равный 4%. Это значит, что лампочка в 100 Ватт будет давать только 4 Ватта световой энергии в видимой части спектра излучения, а остальные 96 Ватт уйдут на нагревание атмосферы. Физики разработали люминисцентные лампы с КПД 30%. Правительство США обложило большим налогом производителей ламп накаливания и дало субсидии и налоговые льготы для тех, кто может и хочет производить люминисцентные лампы. В результате лампы накаливания исчезли у населения.
Спустя еще 10 лет физики разработали другие лампы с КПД 80%. Правительство США проделывает ту же процедуру. Теперь исчезли люминисцентные лампы.
Все эти государственные меры позволили не строить в США 17 новых мощных ТЭЦ.
Экономический и экологический эффект огромен.
Далее, химики синтезировали новое вещество, оказавшееся замечательным хладоагентом для холодильной техники, правда, пришлось изменить технологическую схему холодильников. Правительство снова щелкает кнутом налогов и раздает пряники субсидий и льгот. Вся страна за год сменила свои бытовые холодильники, обеспечивающие высокую эффективность. Это «холодильное» мероприятие правительства позволило не строить еще 7 мощных ТЭЦ.
Налицо разумное управление экономикой: если уж электроэнергия производится так не эффективно, то надо заставить население высокоэффективно ее использовать.
Тема 3.1. Теплопроводность
Тема 3.2. Конвективный теплообмен Тема 3.3. Процессы теплопередачи
Раздел 3. Теплопередача
Тема 3.1. Теплопроводность
Теплотехника – область науки и техники, занимающаяся вопросами получения и использования теплоты.
Различают два вида использования теплоты – энергетическое и технологическое. Энергетическое использование теплоты основывается на процессах, преобразующих теплоту в механическую работу. Технологическое использование теплоты основывается на реализации теплоты для целенаправленного изменения физико-химических свойств при осуществлении различных технологических процессов. К устройствам, в которых непосредственный подвод теплоты используется для технологических целей, относятся различные печи, сушилки, отопительные приборы, калориферы и т.д.
Наука, изучающая закономерности теплообмена между телами, называется теорией теплопередачи.
Теплопроводность – это перенос тепла при непосредственном соприкосновении тел с различной температурой, когда перенос энергии осуществляется микрочастицами за счет их «теплового» движения. В чистом виде теплопроводность наблюдается в твердых телах, а в жидкостях и газах – лишь в неподвижных средах. При этом в жидкостях и твердых телах (диэлектриках) перенос энергии осуществляется путем упругих волн, в газах – путем диффузии атомов или молекул, а в металлах, путем диффузии свободных электронов.
Конвективный перенос теплоты обусловлен массовым движением макрочастиц среды – теплота переносится движущейся средой. Такой способ теплопереноса возможен лишь в жидкостях и газах, при этом всегда сопровождается теплообменом между частицами посредством теплопроводности. В свою очередь, конвекция бывает свободной и вынужденной. Свободная конвекция происходит в результате разности плотностей жидкости или газа в различных точках занимаемого ими объема вследствие разных температур, вынужденная – когда перемещение частиц жидкости или газа происходит под действием внешних сил (с помощью насосов, компрессоров).
Тепловое излучение – это перенос энергии в форме электромагнитных колебаний, сопровождаемый переходом лучистой энергии в тепловую и наоборот. Этот вид переноса тепла имеет место между телами любого агрегатного состояния независимо от того, удалены ли они друг от друга или соприкасаются между собой.
В реальных условиях теплота чаще всего передается одновременно двумя или даже тремя способами. Однако обычно преимущественное значение имеет какой-нибудь один способ.
Наиболее распространенным случаем в практике является перенос тепла от одного теплоносителя к другому через разделяющую их стенку. Такой вид теплообмена называют теплопередачей. Процесс теплопередачи включает три стадии:
1) перенос теплоты средой, имеющей более высокую температуру, стенке;
2) перенос теплоты в стенке;
3) перенос теплоты от нагретой стенки к среде с более низкой температурой.
Перенос теплоты в стенке происходит путем теплопроводности. Передача теплоты от теплоносителя к стенке и от нагретой стенки к более холодной среде называют теплоотдачей.
Особое место среди тепловых процессов занимают процессы, сопровождающиеся изменением агрегатного состояния теплоносителей (кипение, конденсация пара и т.д.).
В процессе переноса теплоты температура в общем случае изменяется в пространстве и во времени: t f x , , ,у z τ ,
где t – температура; x, у, z – координаты; – время. Пространство с различными температурами в отдельных его точках является температурным полем. Изменение температуры в данной точке пространства со временем характеризуют мгновенными температурами.
Процессы, в которых поля температур постоянны во времени, являются установившимися или стационарными. Они соответствуют непрерывно действующим аппаратам. Если же распределение температур в телах, участвующих в теплообмене, изменяется во времени, то процесс считается неустановившимся или нестационарным. Такие процессы протекают в аппаратах периодического действия. Геометрическое место точек, имеющих одинаковую температуру, образует изотермическую поверхность. Так как в одной и той же точке пространства одновременно не может быть двух различных температур, то изотермические поверхности разных температур друг с другом не пересекаются. Все они либо замыкаются на себя, либо кончаются на границах тела. Изменение температуры в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности. При этом наиболее резкое изменение происходит в направлении нормали n к изотермическим поверхностям (рис. 3.1).
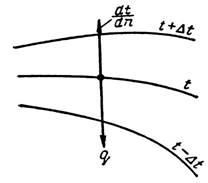
Рис. 3.1. К определению температурного градиента
Предел отношения изменения температуры t к расстоянию между изотермами по нормали n называют температурным градиентом grad t :
t dt
lim ![]()
![]() grad .t
grad .t
n n 0 dn
Температурный градиент является вектором, направленным по нормали к изотермической поверхности. Его положительным направлением считается направление в сторону возрастания температуры. Значение температурного градиента, взятое с обратным знаком, называют падением температуры.
Количество тепла, проходящее через данную поверхность за время , называют тепловым потоком Q [Дж]. Тепловой поток, проходящий в единицу времени через 1 м2 поверх-
ности, носит название удельного теплового потока q Дж/ м 2 c = Вт/м 2 .
Величина теплового потока зависит от теплофизических свойств теплоносителя. Непосредственное влияние на процесс переноса тепла оказывают температура, теплоемкость, температуропроводность, энтальпия, теплота фазового превращения.
Теплопроводность представляет собой форму передачи теплоты путем непосредственного соприкосновения отдельных частиц тела, имеющих различную температуру. При этом процесс теплообмена происходит вследствие передачи энергии микродвижения одних элементарных частиц другим.
В практических условиях, теплопроводность в наиболее чистом виде наблюдается в твердых телах. В жидкостях и газах возможность чистой теплопроводности практически исключается, так как в этом случае перенос теплоты осуществляется не только микрочастицами, но и макрочастицами среды (которые по размерам во много раз превосходят длины свободного пробега микрочастиц или амплитуду их колебаний), организующими перемещение жидкостей и газов.
![]() В основе теории
теплопроводности лежит закон Фурье[23], связывающий количество
переносимой внутри тела теплоты с существующим температурным полем. Согласно
этому закону количество тепла dQ
, переданное посредством теплопроводности, пропорцио-
В основе теории
теплопроводности лежит закон Фурье[23], связывающий количество
переносимой внутри тела теплоты с существующим температурным полем. Согласно
этому закону количество тепла dQ
, переданное посредством теплопроводности, пропорцио-
t
нально падению температуры по нормали , времени d и площади сечения dF , перn
![]() пендикулярного направлению
распространения тепла: dQ
t
dFd
пендикулярного направлению
распространения тепла: dQ
t
dFd
n
либо
q
t
gradt![]() .
.
n
Величины dQ и t имеют тот или иной знак в зависимости от принятого направn
ления нормали. Если за положительное направление принято направление теплового по-
t
![]() тока в сторону
убывающих температур, то имеет отрицательное значение, так как n
тока в сторону
убывающих температур, то имеет отрицательное значение, так как n
направления теплового потока и градиента температур не совпадают. Тогда
dQ ![]() t
dFd
t
dFd
n
или q ![]() t
.
t
.
n
Коэффициент пропорциональности в уравнениях является коэффициентом теплопроводности и показывает, какое количество теплоты передается в единицу времени через единицу поверхности при падении температуры в 1 С на единицу длины:
Q Дж Вт
![]()
Ft l
м
сК м2
мК (l
– линейный размер, м).
Ft l
м
сК м2
мК (l
– линейный размер, м).
Значение коэффициентов теплопроводности зависит от структуры, удельного объема, влажности, давления и температуры. Численные значения определяются опытным путем. Для наиболее распространенных веществ эти значения приводятся в справочной литературе. При выборе из справочных таблиц следует учитывать соответствие физических свойств вещества – структуры, влажности, температуры и т.д. – и при необходимости вводить поправки.
Коэффициент теплопроводности твердых тел является функцией температуры:
0(1 вt),
где 0 – коэффициент теплопроводности при 0 С; в – постоянная для данного веще-
ства; для большинства металлов в < 0, т.е. уменьшается с увеличением температуры, для большинства неметаллов (керамика, например) в > 0, т.е. увеличивается с повышением температуры.
В случае твердых пористых тел с порами, заполненными воздухом, коэффициент теплопроводности
тв 1 ,
![]() 1 2
1 2
где тв – теплопроводность твердой фазы; – порозность тела.
Зависимость коэффициента теплопроводности газов от температуры может быть представлена уравнением Сатерленда:
3
![]() 0 cр
Т0
С Т 2
,
0 cр
Т0
С Т 2
,
ср0 Т С Т0
где ср и ср0 – удельные теплоемкости газа, соответственно при температурах Т и Т0; С – постоянная для данного газа. Значения С для некоторых газов приведены в таблице 3.1.
|
Газ |
С, К |
Температурные границы для С, ºК |
|
Азот |
118 |
288–373 |
|
Аммиак |
377 |
288–457 |
|
Водород |
71,7 |
253–573 |
|
Воздух |
114 |
273–573 |
|
Двуокись серы |
416 |
288–373 |
|
Двуокись углерода |
240 |
253–573 |
|
Кислород |
138 |
288–463 |
|
Метан |
198 |
288–373 |
|
Окись углерода |
118 |
289–373 |
3
![]() Таб. 3.1. Значения
коэффициента С в уравнении
0
cр
ТТ
С0С
Т 2
Таб. 3.1. Значения
коэффициента С в уравнении
0
cр
ТТ
С0С
Т 2
ср0 Т0
Коэффициенты теплопроводности жидкостей, как указано в подразделе 7.3, как правило, с увеличением температуры уменьшаются (исключение составляют вода и глицерин), изменение давления на величину практически не влияет. Приближенно коэффициент теплопроводности жидкостей можно рассчитать, пользуясь эмпирической формулой Вебера:
 .
.
В этой формуле и ср – плотность и удельная теплоемкость жидкости, соответственно; М – молярная масса; r – удельная теплота парообразования; Ткип – абсолютная температура кипения.
Распределение температуры в теле, описывается дифференциальным уравнением теплопроводности, которое при принятых допущениях, а именно: тело однородно и изотропно; физические параметры тела постоянны во времени и пространстве; температурные деформации рассматриваемого элементарного объема малы по сравнению с самим объемом; внутренние источники теплоты распределены в рассматриваемом объеме равномерно; макрочастицы тела неподвижны относительно друг друга; имеет следующий вид:
![]()
![]()
a c x2
y2
z2
cv , где
– время, сек; a
a c x2
y2
z2
cv , где
– время, сек; a
![]() c
– коэф-
c
– коэф-
фициент температуропроводности, характеризующий скорость изменения температуры в м2
любой точке
тела, ![]() ;
сек
;
сек
c – теплоемкость тела; – плотность тела; qv – объемная плотность тепловыделе-
ния, вm/м3; t – температура; – оператор Лапласа.
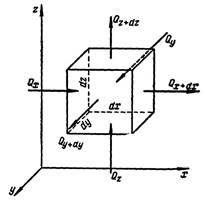
Рис. 3.2. К выводу дифференциального уравнения теплопроводности
Уравнение называется дифференциальным уравнением теплопроводности.
Чтобы получить конкретное решение уравнения для рассматриваемого случая, необходимо ввести полное математическое описание данного конкретного процесса теплопроводности. Эти частные особенности называются условиями однозначности или краевыми условиями, включающими:
I) Геометрические условия (форма, размеры тела);
II) Физические условия (физические свойства тела и его физические параметры);
III) Начальные условия (распределение температуры в теле в начальный момент времени);
IV) Граничные условия, определяющие взаимодействие тела с окружающей средой.
1. Граничные условия первого рода. Задается распределение температуры на поверхности тела, как функция координат и времени: tc f x,y,z,,
2. Граничные условия второго рода. Задается распределение плотности потока на поверхности тела, как функция координат и времени: qc f x,y,z,
В частном случае, когда плотность теплового потока на поверхности тела остается постоянной, имеем qc q0 const .
3. Граничные условия третьего рода. Задается температура окружающей среды tж и закон теплообмена между поверхностью тела и окружающей средой: q tc tж если tс tж , где – коэффициент теплообмена, представляющий собой плотность теплового потока подведенного (отведенного) к единице поверхности тела при разности температур между поверхностью тела и окружающей среды 10С, вm/м2град.
4. Граничные условия четвертого рода. Отражают условия теплообмена системы тел имеющих различные коэффициенты теплопроводности. Между телами предполагается
![]()
![]() идеальный контакт.
Тогда 1t1
2t2 ,
где 1– коэффициент
теплопроводности
идеальный контакт.
Тогда 1t1
2t2 ,
где 1– коэффициент
теплопроводности
n с n
первого тела; 2 – коэффициент теплопроводности второго тела.
Для решения практических задач по переносу тепла теплопроводностью помимо закона Фурье необходимо знать распределение температур в пространстве и во времени, так как Q f x y z( , , ,).
С этой целью в однородном и изотропном твердом теле выделяется бесконечно малый прямоугольный параллелепипед с гранями dx, dy, dz и постоянной плотностью , удельной теплоемкостью ср и коэффициентом теплопроводности . Поток тепла, проходящий через этот параллелепипед (рис. 3.2), можно разложить на три составляющие в направлениях осей координат.
Согласно закону Фурье в направлении оси x за промежуток времени d к грани dydz параллелепипеда подводится количество тепла.
Qx
dydz
![]() t
d.
t
d.
x
Через противоположную грань параллелепипеда, находящуюся на расстоянии dx, выходит в направлении оси х тепло Qx dx :
![]() Qx
dx dydz t t dx d ,
x x
Qx
dx dydz t t dx d ,
x x
либо
t 2t
![]() Qx
dx dydz x x2
dx d ,
Qx
dx dydz x x2
dx d ,
t
так как температура на противоположной
грани равна t ![]() dx
.
dx
.
x
Следовательно, изменение количества тепла (приращение или убыль) в параллелепипеде по направлению оси х составит:
dQx Qx Qx dx
t t 2t 2t
![]() dydz
dydz ![]() x d
dydz
x x2
dx d
dydzdx
x d
dydz
x x2
dx d
dydzdx ![]() x2
d либо
x2
d либо
2
dQx
![]()
t2 dVd,
t2 dVd,
x
где dV – объем параллелепипеда.
Аналогично выразятся изменения количеств тепла в параллелепипеде по направлению осей у и z:
2t 2t
dQy ![]() 2 dVd; dQz
2 dVd; dQz ![]() 2 dVd .
2 dVd .
y z
Полное изменение тепла в объеме параллелепипеда составит:
2t 2t 2t
![]() dQ dQ dQ dQ x
y
z
x2 y2
z2
dVd.
dQ dQ dQ dQ x
y
z
x2 y2
z2
dVd.
Поток тепла dQ приводит к изменению температуры параллелепипеда на величину
t ![]() d, что влечет за
собой изменение теплосодержания параллелепипеда за время d:
d, что влечет за
собой изменение теплосодержания параллелепипеда за время d:
dQ c dVp ![]() td.
td.
Из уравнений (7.21) и (7.22) следует:
t 2t 2t 2t 2t 2t 2t
![]()
![]() 2 2 2 a x2 y2 z2 ,
cp x y z
2 2 2 a x2 y2 z2 ,
cp x y z
либо ![]() t
a2t .
t
a2t .
Здесь множитель a – коэффициент температуропроводности.
Полученное уравнение является дифференциальным уравнением теплопроводности Фурье, представляющим распределение температур во времени и пространстве при неустановившемся процессе.
t
При установившемся процессе
теплопроводности ![]()
0, тогда
0, тогда
2t 2t 2t
![]() 0.
0.
x2 y2 z2
Таким образом, дифференциальное уравнение теплопроводности дает возможность решать задачи как при установившемся, так и при неустановившемся тепловом потоке.
![]() Однако
Однако
![]() t
a2t
и x2t2 y2t2 z2t2 0 определяют передачу
тепла теплопроводно-
t
a2t
и x2t2 y2t2 z2t2 0 определяют передачу
тепла теплопроводно-
стью в самом общем виде, без учета формы тела, через которое проводится тепло, его свойств и свойств окружающей среды. При решении конкретных задач эти уравнения дополняются условиями однозначности или краевыми условиями.
Условия однозначности включают в себя:
1) геометрические параметры, характеризующие форму и линейные размеры тела, в котором протекает процесс;
2) физические параметры, описывающие физические свойства среды и тела (λ, с, ρ и т.д.);
3) временные или начальные условия, характеризуют распределение температур в рассматриваемом теле в начальный момент времени;
4) граничные условия, описывающие взаимодействие данного тела с окружающей средой.
Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае этот закон может быть записан в виде: t f x y z( , , ), так как 0.
При равномерном распределении температуры в теле при 0, t t 0 const.
Граничные условия могут быть заданы несколькими способами.
1. Задается распределение температуры по поверхности тела для каждого момента времени (граничные условия первого рода): tпов f x y z( , , ,).
В частном случае, когда температура на поверхности является постоянной на протяжении всего времени протекания процесса теплообмена, последняя зависимость упрощается до вида tпов const.
2. Задаются значения теплового потока для каждой точки поверхности тела в любой момент времени (граничные условия второго рода). Аналитически это можно представить таким образом: qпов f x y z( , , ,), где qпов – плотность теплового потока на поверхности тела.
В простейшем случае плотность теплового потока на поверхности и во времени остается постоянной: qпов q const.
3. Задаются температура окружающей среды tср и закон теплообмена между поверхностью тела и окружающей средой (граничные условия третьего рода). Это граничное условие характеризует закон теплообмена между поверхностью и окружающей средой в процессе охлаждения и нагревания тела.
Процесс теплообмена между поверхностью тела и средой относится к очень сложным процессам и зависит от большого количества параметров. Подробно эти вопросы будут рассмотрены в дальнейшем.
![]() t 2
заданными условиями Дифференциальное уравнение теплопроводности a t с
t 2
заданными условиями Дифференциальное уравнение теплопроводности a t с
однозначности дает полное математическое описание краевой задачи теплопроводности. Поставленная таким образом задача разрешается аналитическим, численным или экспериментальным методом. В случае экспериментального решения задач теплопроводности используют методы физического или математического моделирования.
В инженерной практике часто приходится решать задачи стационарной теплопроводности через плоскую, цилиндрическую и сферическую стенки. К этим задачам, в частности, относится расчет тепловой изоляции аппаратов и трубопроводов.
Теплопроводность плоской стенки. Тепловой поток перемещается через плоскую стенку толщиной δ (рис. 3.3) из однородного материала, имеющего коэффициент теплопроводности .

Рис. 3.3. К выводу уравнения теплопроводности плоской стенки
На наружной поверхности стенки поддерживаются постоянные температуры tcт1 и tcт2 (tcт1 > tcт2). Температура изменяется только в направлении оси х, перпендикулярной плоскости стенки, т.е. температурное поле одномерно, а изотермические поверхности плоские и располагаются перпендикулярно оси х.
2t
В соответствии с дифференциальным
уравнением теплопроводности ![]() 0.
0.
x2
В результате интегрирования этого выражения получим: dt
C dx
1 ; ![]() dt
C1; t
C
x C1 2
. dx
dt
C1; t
C
x C1 2
. dx
Таким образом, температура по толщине плоской стенки при установившемся тепловом режиме изменяется линейно, а градиент температуры сохраняет постоянное значение.
Константы интегрирования C1 и C2 определяют из граничных условий: При x 0, t t cт1; 0, следовательно С2 tcт1 ; dt
При x
, t tcт2; tcт2
С1С2
![]() dx tcт1
, либо
dx tcт1
, либо
![]() С1
dt tcт1
tcт2
. dx
С1
dt tcт1
tcт2
. dx
С учетом найденных констант:
![]() t tcт2
tcт1
x t
cт1 .
t tcт2
tcт1
x t
cт1 .
![]() Дифференцируя
последнее уравнение, имеем: dt
tcт2
tcт1
.
Дифференцируя
последнее уравнение, имеем: dt
tcт2
tcт1
.
dx
Подставив найденные значения температурного градиента в уравнение, выражающее
t
основной закон теплопроводности dQ
![]() dFd, получим
уравнение теплопроводноn
dFd, получим
уравнение теплопроводноn
сти для плоской стенки при стационарном режиме:
![]() dQ tcт2
tcт1
dFd ,
dQ tcт2
tcт1
dFd ,
либо
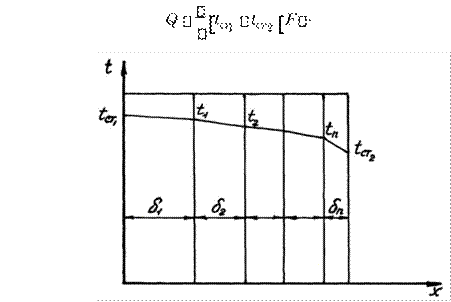
Рис. 3.4. К выводу уравнения теплопроводности плоской многослойной стенки
Отношение (/) носит название тепловой проводимости стенки, а (/) – термического сопротивления стенки.
Если стенка многослойная (рис. 3.4), состоит из n слоев толщиной 1 2, ,...n с коэффициентами теплопроводности 1 2, ,...n соответственно, при этом температуры наружных поверхностей tcт1 и tcт2, а температуры на границе слоев t t1 2, ,...tn1, то при установившемся тепловом режиме тепловой поток Q, проходящий через каждый слой, одинаков и уравнение теплопроводности для каждого из них может быть выражено уравнением:
для 1-го слоя Q 1 tcт1 t F1 , или q 11 tcт1 t1;
1
для 2-го слоя Q 2 t1 t F2 , или q 2 t1 t2;
2 2
для n-го слоя Q n tn1 tст2 F, или q nn tn1 tст2 . n
Складывая левые и правые части данного выражения, получим уравнение теплопроводности плоской многослойной стенки для стационарного режима:
11 22 nn tcт1 tcт2 q
либо
![]() Q cт1
tcт2
F , t n
Q cт1
tcт2
F , t n
i1
где i – порядковый номер слоя.
Таким образом, общее термическое сопротивление плоской многослойной стенки равно сумме термических сопротивлений отдельных слоев стенки при условии, что слои плотно прилегают друг к другу. Внутри каждого слоя линия изменения температуры (рис. 3.4) – прямая, но для многослойной стенки в целом она представляет собой ломаную линию.
Рис. 3.5. К выводу уравнения теплопроводности цилиндрической стенки
Теплопроводность цилиндрической стенки. В однородной цилиндрической стенке длиной L (рис. 3.5) температура в случае одномерного стационарного поля изменяется только в радиальном направлении, поэтому для поверхности произвольного радиуса r уравнение Фурье можно представить в виде
t t dQ ![]() F
F
![]() 2rL.
2rL.
n r
Для кольцевого слоя с радиусом r и толщиной dr, выделенного внутри стенки (рис. 3.5), при внутреннем и наружном радиусах соответственно r1 и r2 и температурах на внутренней и наружной поверхностях стенки tcт1 и tcт2, согласно уравнению
t t dQ ![]() F
F
![]() 2rL имеем:
2rL имеем:
n r
r2 tст2 dr 2 L
![]()
r
Q
dt .
r
Q
dt .
r1 tст1
В результате интегрирования последнего выражения получим:
![]() rr12
2 L
tcт2
tcт1
rr12
2 L
tcт2
tcт1
ln
Q
Q 2 L t cт1 tcт2 .
либо
![]() 1 r
1 r
r1
r2 dн (dн и dв – наружный и внутренний диаметры цилиндра Если учесть, что
r1 dв
соответственно), то:
2 L t
Q cт1 tcт2 .
![]() 1 d
1 d
dв
Данные уравнения являются уравнениями теплопроводности цилиндрической стенки при установившемся процессе теплообмена. Они показывают, что по толщине цилиндрической стенки (в отличие от плоской) температура изменяется криволинейно – по логарифмическому закону. При этом влияние кривизны стенки учитывается коэффициентом кри-
dн . При dн < 2 значевизны φ, значение которого определяется отношением диаметров
dв dв ние φ близко к единице, а это значит, что влиянием кривизны стенки в этом случае можно пренебречь и тогда расчет теплопроводности тонкостенных цилиндров можно производить по формулам для плоской стенки.
Для многослойной цилиндрической стенки, состоящей из n слоев (плотно прилегающих друг к другу), по аналогии с выводом, приведенным для однослойной стенки:
Q cт1 tcт2 , 2 L t
![]() n 1 lndi1
i1
di
n 1 lndi1
i1
di
где i – порядковый номер слоя стенки.
В многослойной цилиндрической стенке температура внутри каждого слоя изменяется по логарифмическому закону, но для всей стенки в целом температурная линия представляет собой ломаную кривую (рис. 3.6).
Рис. 3.6. Теплопроводность многослойной цилиндрической стенки
Температуры прилегающих слоев t t2 3, ,...tn в случае необходимости могут быть рассчитаны из равенств:
Q 2 L t( 1 t2) 2 L t( 2 t3) 2 L t( n1 tn) .
![]() 1 d 1 d
1 d 1 d ![]() 1
1
1 d1 1 d3 1 dn1
Рис. 3.7. К выводу уравнения теплопроводности сферической стенки
Теплопроводность сферической стенки. Стенка полого шара состоит из однородного материала, коэффициент теплопроводности которого постоянен и равен . Внутренняя и внешняя поверхности шара поддерживаются при постоянных температурах tcт1 и tcт2
. Температура изменяется только в направлении радиуса шара, изотермические поверхности представляют собой концентрические шаровые поверхности. Радиусы внутренней и внешней поверхности соответственно r1 и r2 (рис. 3.7).
В соответствии с законом Фурье количество тепла, проходящее через шаровой слой толщиной dr и радиусом r
Q ![]() dt
F
dt
F
![]() dt 4r2.
dt 4r2.
dr dr
В результате разделения переменных и интегрирования этого выражения в соответствующих пределах, получим:
r2 tст2
![]() r1
drr2
4Q tст1dt ,
r1
drr2
4Q tст1dt ,
откуда
![]() Q
cт1 tcт2
2tcт1 tcт2
d2d d1
2d tcт1
tcт2,
4 t
Q
cт1 tcт2
2tcт1 tcт2
d2d d1
2d tcт1
tcт2,
4 t
1 1 1 1
r1 r2 d1 d2
где d1 и d2 – диаметры внутренней и внешней поверхности соответственно.
Данные уравнения являются расчетными формулами теплопроводности сферической стенки. Как следует из них, при = сonst температура в сферической стенке меняется по закону гиперболы.
По аналогии с плоской и цилиндрической стенками для многослойной сферической стенки
4 t
Q cт1 tcт2 .
![]() n
1 di1
di
n
1 di1
di
i1 i di1 di
В тепловых процессах одновременно с теплопроводностью и конвекцией почти всегда наблюдается и тепловое излучение, причем, чем выше температура тела, отдающего тепло, тем большее количество тепла передается в виде лучистой энергии.
Тепловое излучение представляет собой процесс распространения внутренней энергии излучающего тела путем электромагнитных волн. При поглощении электромагнитных волн какими-либо другими телами они вновь превращаются в энергию теплового движения молекул. Источниками электромагнитных волн являются заряженные материальные частицы, т.е. электроны и ионы, входящие в состав вещества. По своей природе тепловое излучение аналогично излучению света, оба они представляют собой один вид энергии – лучистой – и подчиняются одним и тем же законам отражения, преломления и поглощения. Соответственно этому тепловое излучение характеризуется длиной волны. Однако в отличие от видимых световых лучей, имеющих длину волн 0,4÷0,8 мкм, длина волн теплового излучения лежит в основном в невидимой (инфракрасной) части спектра и составляет 0,8÷40 мкм.
Все тела излучают и поглощают лучистую энергию непрерывно. Интенсивность излучения зависит от природы тела, его температуры, длины волны, состояния поверхности, а для газов – еще от толщины слоя и давления. Твердые и жидкие тела имеют значительные поглощательную и излучательную способности. Вследствие этого в процессах лучистого теплообмена участвуют лишь тонкие поверхностные слои. Поэтому в этих случаях тепловое излучение приближенно можно рассматривать как поверхностное явление. Газы и пары характеризуются объемным характером излучения, в котором участвуют все частицы объема вещества. Излучение всех тел зависит от температуры. С увеличением температуры тела его энергия излучения увеличивается, так как увеличивается внутренняя энергия тела.
При этом изменяется не только значение этой энергии, но и спектральный состав. При увеличении температуры повышается интенсивность коротковолнового излучения и уменьшается интенсивность длинноволнового излучения. В процессах излучения зависимость от температуры значительно большая, чем в процессах теплопроводности и конвекции. Вследствие этого при высоких температурах основным видом переноса тепла может быть тепловое излучение.
Лучистая энергия распространяется в однородной и изотропной среде прямолинейно. В отличие от теплопроводности и конвекции, лучистый теплообмен происходит не только между соприкасающимися, но и между удаленными друг от друга телами. Поток лучей, испускаемый нагретым телом, попадая на поверхность другого лучеиспускающего тела, частично поглощается, частично отражается (при этом угол падения равен углу отражения) и частично проходит сквозь тело без изменений, т.е.
Q Qпогл Qотр Qпр ;
Q Q Q
![]() то
есть погл отр
пр
1,
то
есть погл отр
пр
1,
Q Q Q
где Q – общая энергия падающих на тело лучей; Qпогл – энергия, поглощенная телом; Qотр– энергия, отраженная от поверхности тела; Qпр – энергия лучей, проходящих сквозь тело без изменений.
![]() Таким
образом, отношения погл
, отр
и пр
характеризуют поглощательную, от-
Таким
образом, отношения погл
, отр
и пр
характеризуют поглощательную, от-
Q Q Q
ражательную и пропускательную способности тела. Если тело полностью поглощает пада-
![]() Qпогл 1, а Qотр и Qпр равны нулю, то
оно носит ющую на него лучистую энергию, т.е.
Qпогл 1, а Qотр и Qпр равны нулю, то
оно носит ющую на него лучистую энергию, т.е.
Q Q Q
Qотр
название абсолютно черного. При полном отражении телом
лучистой энергии, ![]() 1
, а
1
, а
Q
Qпогл Q![]() пр 0, такие тела называют абсолютно
белыми. Наконец, если тело пропускает
пр 0, такие тела называют абсолютно
белыми. Наконец, если тело пропускает
Q Q
Q
все падающие на него лучи, не поглощая их и не отражая, ![]() пр
1,
а Qпогл
Q
пр
1,
а Qпогл
Q![]() отр
0
его
отр
0
его
Q Q Q
называют абсолютно прозрачным или диатермичным.
В природе не существует абсолютно черных, абсолютно белых и абсолютно прозрачных тел. Все тела в той или иной степени поглощают, отражают и пропускают сквозь себя падающие на них лучи, т.е. являются серыми. Однако твердые тела и жидкости практически непрозрачны для тепловых лучей, а большинство газов, наоборот, диатермичны.
Закон Стефана-Больцмана[24]. Количество тепла, излучаемого единицей поверхности тела в единицу времени, называют лучеиспускательной способностью тела Е, Вт/м2 :
E
![]() Q
.
Q
.
F
Как указывалось ранее, энергия излучения зависит от длины волн и температуры Т.
![]() Характеристикой
энергии излучения по длинам волн служит интенсивность излучения I
– лучеиспускательная способность тела в интервале длин волн от
до
+ d,
отнесенная к этому интервалу d, т.е. dE .
Характеристикой
энергии излучения по длинам волн служит интенсивность излучения I
– лучеиспускательная способность тела в интервале длин волн от
до
+ d,
отнесенная к этому интервалу d, т.е. dE .
I
d
Лучеиспускательная способность тела E является интегральной характеристикой, которая учитывает энергию излучения волн всех длин от λ = 0 до λ = ∞. Следовательно,
E Id .
0
На основании электромагнитной теории света Планком аналитически была определена функциональная зависимость интенсивности излучения I0 от температуры и длины волн для абсолютно черного тела. Согласно этой зависимости
![]() I0
ecc21
T51
,
I0
ecc21
T51
,
где c1 – константа, равная 3,74∙10–16 Вт/м2; с2 – константа, равная 1,44∙10–2 (м∙К).
![]() Интегрирование
выражения E 0
Id с учетом I0 ecc21
T51
дает зависимость
Интегрирование
выражения E 0
Id с учетом I0 ecc21
T51
дает зависимость
для определения лучеиспускательной способности абсолютно черного тела Е0:
E0 к Т0 4 ,
где к0 – константа излучения абсолютно черного тела, к0 = 5,67∙10–8 Вт/(м2∙К4).
![]() Зависимость E0 к Т0 4 носит название закона
Стефана[25]–Больцмана, так как была
найдена экспериментально Стефаном и подтверждена Больцманом до того, как Планк
вывел соотношение I0
ecc21
T51
.
Зависимость E0 к Т0 4 носит название закона
Стефана[25]–Больцмана, так как была
найдена экспериментально Стефаном и подтверждена Больцманом до того, как Планк
вывел соотношение I0
ecc21
T51
.
Таким образом, согласно закону Стефана–Больцмана, лучеиспускательная способность абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры.
При проведении технических расчетов выражение E0 к Т0 4 удобнее использовать в виде 4
T
E0 C0 ![]() ,
,
100
где С0 – коэффициент излучения абсолютно черного тела, равный
С0 = k0∙108 = 5,67 Вт/(м2∙К4).
Исследования показали, что закон Стефана-Больцмана применим не только к абсолютно черным телам, но и к серым. В этом случае его записывают в виде
4
E C ![]() T
T
100
(C по аналогии с абсолютно черным телом называют коэффициентом излучения серых тел).
Отношение коэффициентов излучения данного тела и абсолютно черного С/С0 = носит название относительной излучательной способности или степени черноты данного тела. С учетом этого понятия закон Стефана-Больцмана принимает вид
4
E C0
![]() T .
T .
100
Закон Кирхгофа устанавливает соотношение между лучеиспускательной и поглощательной способностями тел. Это соотношение может быть получено из рассмотрения процесса обмена лучистой энергией между абсолютно черным и серым телами (рис. 3.8).
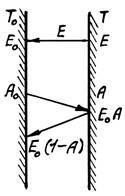
Рис. 3.8. К выводу закона Кирхгофа
Поверхности рассматриваемых тел параллельны и расположены на расстоянии, при котором излучение каждого из тел попадает на другое. Абсолютно черное тело имеет температуру T0, лучеиспускательную способность E0 и поглощательную A0 = 1, серое тело имеет соответственно Т, Е и А, при этом Т > T0. Излучение Е попадает на абсолютно черное тело и целиком им поглощается. Излучение E0 попадает на серое тело. При этом часть этого излучения, равная E0А, поглощается, а другая часть, равная E0(1 – А), отражается на абсолютно черное тело и поглощается им. В результате этого обмена абсолютно черное тело получает суммарное количество энергии:
Q E E0(1 A)E0 E E A0 .
При выравнивании температур обоих тел наступает тепловое равновесие, при котором Q = 0, т.е. E E A 0 0;E E A0 . Следовательно,
![]() E
E0 .
E
E0 .
A
Последнее соотношение является математическим выражением закона Кирхгофа[26], согласно которому отношение лучеиспускательной способности тел к их поглощательной способности для всех тел одинаково, равно лучеиспускательной способности абсолютно черного тела при той же температуре и зависит только от температуры.
4
В результате подстановки значений E и E0 из равенств E C
![]() T
и
T
и
100
4
T E
E C0 ![]()
в соотношение
в соотношение ![]()
E0 получаем
E0 получаем
100 A
C AC0 .
Так как C C0, то A , т.е. способность тела к поглощению излучения численно равна степени его черноты. Учитывая, что и A изменяются в пределах от 0 до 1, из равен-
E
ства ![]()
E0 следует, что
лучеиспускательная способность реального тела всегда меньше
E0 следует, что
лучеиспускательная способность реального тела всегда меньше
A
лучеиспускательной способности абсолютно черного тела при той же температуре.
Закон Ламберта[27] определяет изменение интенсивности излучения по различным направлениям. Согласно этому закону излучение энергии элементом поверхности dF1 в направлении элемента dF2 (рис. 3.9) пропорционально излучению dQ (по направлению нормали к dF1 ), телесному углу dψ (под которым виден элемент dF2 из элемента dF1 ) и косинусу угла φ, образованного прямой, соединяющей элементы dF1 и dF2 , и нормалью к элементу dF1 .
Рисунок 3.9. К формулировке закона Ламберта
При этом лучеиспускательная способность в направлении нормали в раз меньше полной лучеиспускательной способности тела.
Таким образом, количество энергии, излучаемой элементом dF1 в направлении элемента dF2 :
dQ ![]() 1
EdcosdF1.
1
EdcosdF1.
Тема 3.2. Конвективный теплообмен
Конвективным теплообменом называют процесс теплообмена при движении жидкости или газа. При этом перенос теплоты осуществляется одновременно конвекцией и теплопроводностью. Под конвекцией теплоты понимают перенос тепла при перемещении макрочастиц жидкости или газа в пространстве из области с одной температурой в область с другой температурой. Конвенция возможна лишь в движущейся среде, в которой перенос теплоты неразрывно связан с переносом самой среды. Конвекция теплоты всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно происходит соприкосновение отдельных частиц, имеющих различные температуры.
В зависимости от причины, вызывающей
движение жидкости или газа, различают вынужденную и естественную
конвекции. Вынужденная конвекция происходит под воздействием внешних сил –
разности давлений, создаваемой насосом, вентилятором, мешалкой, ветром или иным
каким-либо источником. Естественная конвекция возникает вследствие изменения
плотности самой жидкости или газа в результате термического расширения.
Подъемная сила, обусловливающая свободное движение частиц или естественную
конвекцию, выражается величиной 1g
, а ускорение, вызываемое этой силой, равно 1g![]() 1
( и
1
( и
1 – плотности жидкости в двух ее точках при температурах t и t1 ; g – ускорение силы тяжести). Если объемный коэффициент температурного расширения жидкости или газа , то
![]() 1
1 1t t 1
1
t
.
1
1 1t t 1
1
t
.
1 1
Конвективный теплообмен между потоками жидкости или газа и поверхностью соприкасающегося с ними твердого тела носит название конвективной теплоотдачи или просто теплоотдачи. Следовательно, конвективная теплоотдача является результатом двух параллельно протекающих процессов переноса тепла: собственно, теплопроводности и теплообмена, обусловленного движением жидкости или газа. В зависимости от свойств последних и характера их движения вклад каждого из двух процессов может быть различным, но при всех условиях интенсивность теплообмена неразрывно связана с характером движения жидкости или газа. В связи с этим различают теплоотдачу при свободной или естественной конвекции, при ламинарном и турбулентном режимах течения.
При свободной конвекции более нагретые частицы, имеющие меньшую плотность, поднимаются вверх, их сменяют боле холодные частицы, которые, опускаясь вниз и нагревшись, также движутся кверху; в результате возникают конвективные токи. В этом случае теплоотдача зависит от форм и размеров твердой поверхности, температуры жидкости (газа), коэффициента объемного расширения и других физических свойств (, , μ, cp ), а также от ускорения силы тяжести. Вместе с тем скорость движения жидкости не оказывает влияния на теплоотдачу, так как она является функцией независимых переменных.
При ламинарном режиме движения теплоотдача определяется как вынужденным, так и свободным движением потоков жидкости или газа. Если естественная конвекция отсутствует (либо ею можно пренебречь), то перенос тепла по нормали к поверхности осуществляется лишь за счет теплопроводности жидкости (газа). При наличии же свободной конвекции неизбежно возникает турбулизация потока и перенос тепла усиливается. Наибольшая турбулизация возникает при вертикальном положении твердой поверхности и противоположном направлении свободного и вынужденного движений. При горизонтальном положении поверхности свободное движение жидкости или газа создает довольно сильную турбулизацию, независимо от направления теплового потока.
На рис. 3.10 показана осциллограмма колебаний скорости и температуры в неподвижной точке турбулентного потока, имеющего среднюю скорость течения wср. Мгновенная скорость в этой точке w пульсирует около некоторого среднего во времени значения wср, при этом изменение абсолютной скорости сопровождается еще и изменением направления мгновенной скорости. Отклонение мгновенной скорости w от средней во времени wср носит название пульсаций скорости или пульсационной скорости w'. При этом w = wср + w', т.е. турбулентное движение состоит из регулярного течения, описываемого осредненными значениями скоростей, и из наложенного на него хаотического пульсационного течения.

Рис. 3.10. Изменение скорости w и температуры t в неподвижной точке турбулентного потока
Наличие конвективного теплообмена изменяет распределение скоростей в потоке по сравнению с распределением в случае изотермического потока. Вместе с тем распределение температур определяется полем скоростей. Это обстоятельство взаимного влияния температурного и скоростного полей необходимо учитывать при точном решении задач о конвективном теплообмене в случае сильного изменения вязкости жидкости или газа с изменением температуры.
Конвективный теплообмен может происходить только в подвижных средах – капельных жидкостях и газах. Обычно подвижную среду условно называют жидкостью независимо от агрегатного состояния вещества.
Тепловой поток Q, Вт, передаваемый при конвективном теплообмене, определяется по формуле Ньютона-Рихмана[28]:
Q tс tжF
где: – коэффициент теплоотдачи, Вт/м2С; F – площадь поверхности теплообмена, м2; tж и t – соответственно температуры жидкости и поверхности стенки, С.
Разность температур (tж-t) иногда называют температурным напором.
Коэффициент теплоотдачи характеризует количество теплоты, которое передаётся конвекцией через единицу поверхности в единицу времени при температурном напоре в 1С и имеет размерность [Дж/см2С] или [Вт/м2С].
Величина коэффициента теплоотдачи зависит от множества факторов, а именно:
1. характера (режима) движения жидкости (ламинарный или турбулентный);
2. природы возникновения движения (естественное или вынужденное);
3. физических свойств движущейся среды – коэффициента теплопроводности , плотности , теплоёмкости с, коэффициента вязкости динамического () или кинематического
(=/), коэффициента объёмного расширения ;
4. скорости движения жидкости w;
5. температур жидкости и стенки tж и t;
6. формы и линейных размеров омываемой стенки (Ф, l1, l2,...).
При движении жидкости возможны два основных режима: ламинарный и турбулентный.
При ламинарном режиме отдельные струйки не смешиваются, и каждая частичка жидкости движется параллельно стенки тела.
При турбулентном режиме каждая частица жидкости помимо поступательного движения совершает поперечное движение в виде вихрей. Чем больше вихрей, тем сильнее перемешивание жидкости и турбулентность потока. Так как процесс переноса теплоты связан с переносом самой подвижной среды, то, очевидно, что интенсивность теплообмена зависит от характера её движения.
При движении жидкости вдоль стенки частицы её, взаимодействуя с поверхностью стенки, а также вследствие шероховатости поверхности стенки, испытывают тормозящее действие со стороны стенки. Непосредственно в слое жидкости, прилегающем к стенке, скорость её изменяется от нуля до её значения в ядре потока. Этот слой называют пограничным слоем. Перенос теплоты в этом слое от жидкости к стенке (или наоборот) осуществляется в основном теплопроводностью, т.е. зависит от величины , которая для жидкостей невысокая, а для газов очень низкая.
Толщина этого пограничного слоя тем меньше, чем выше скорость жидкости. Поэтому интенсивность теплообмена между подвижной жидкостью и стенкой существенно зависит от скорости её движения (а также от физических свойств). Очевидно, что при вынужденном движении жидкости могут быть достигнуты скорости намного более высокие, чем при движении вследствие действия сил тяжести на неравномерно нагретые объёмы среды (т.е. при естественной конвекции). Следует иметь в виду, что в реальных условиях оба механизма побуждения движения жидкости могут иметь место одновременно. При интенсивном турбулентном режиме жидкости влиянием свободной конвекции на интенсивность переноса теплоты можно пренебречь.
Для вывода дифференциального уравнения конвективного теплообмена в установившемся потоке жидкости (газа) выделяют элементарный параллелепипед с гранями dx, dy, dz (рис. 7.2) и составляют для него тепловой баланс, приняв физические параметры λ, ср и ρ постоянными. Скорости движения жидкости в направлении осей x, y и z, соответственно – wx, wy и wz. Температура жидкости t изменяется вдоль граней параллелепипеда. Теплоперенос в жидкости осуществляется путем конвекции и теплопроводности. Все подведенное к параллелепипеду тепло затрачивается только на изменение его энтальпии.
Количество тепла, которое вводится жидкостью путем конвекции по направлению оси х через грань dydz за время dτ,
Qx wx cp t dy dz d .
За это же время через противоположную грань параллелепипеда путем конвекции жидкостью выводится количество тепла
w txρ , Qx dx Q dQ w ctdydzd cx x xρ p τ
p ![]() dydzdτ
dydzdτ
x
или
Qx dx w ctdydzd c txρ p τ p ![]() wxρ
wxρ
wxρ
wxρ ![]() t
dxdydzdτ.
t
dxdydzdτ.
x x
Разность между количествами введенного и выведенного тепла в направлении оси х за время dτ составит:
dQ Q Qx x x dx c tp ![]() wxρ
wxρ
wxρ
wxρ ![]() t
dxdydzdτ.
t
dxdydzdτ.
x x
Аналогично в направлении осей y и z
wyρ t
dQy c
tp ![]() wyρ
wyρ ![]() dxdydzdτ; y y
dxdydzdτ; y y
dQz c tp ![]() wzρ
wzρ
wzρ
wzρ ![]() t
dxdydzdτ .
t
dxdydzdτ .
z z
Полная разность между количествами введенного и выведенного путем конвекции тепла в объеме параллелепипеда за время dτ
![]() dQконв dQx dQy dQz cp t wxρ
wyρ
wzρ
dQконв dQx dQy dQz cp t wxρ
wyρ
wzρ
x y z
t t t
wxρ ![]() wyρ
wyρ ![]() wzρ
wzρ ![]() dxdydzdτ
.
dxdydzdτ
.
x y z
На основании уравнения неразрывности потока
w ρ
![]() x
wyρ
wzρ
0.
x
wyρ
wzρ
0.
x y z
Тогда конвективная составляющая теплового потока
t t t
![]() dQконв
ρc
wp x wy wz dVdτ,
dQконв
ρc
wp x wy wz dVdτ,
x y z
где dV dxdydz – объем параллелепипеда.
Количество тепла, которое вводится в параллелепипед жидкостью путем теплопроводности за время dτ, в соответствии с уравнением
![]() 2t 2t 2t dQтепл
x2
y2
z2
dVd.
2t 2t 2t dQтепл
x2
y2
z2
dVd.
Суммарное количество тепла, подведенное конвекцией и теплопроводностью dQ dQконв dQтепл
t t t 2t 2t 2t
![]()
![]() cpρwx x wy y wz dVd
x2
y2
z2
dVdτ.
cpρwx x wy y wz dVd
x2
y2
z2
dVdτ.
z
Это тепло dQ, согласно первому началу термодинамики, равно изменению энтальпии жидкости в объеме параллелепипеда
t
dQ dV cρ p ![]() dτ.
dτ.
τ
Таким образом,
t t t t 2t 2t 2t
![]()
![]() dV c d p τ c wpρ x
x wy y wz z dVd
x2 y2 z2 dVdτ .
dV c d p τ c wpρ x
x wy y wz z dVd
x2 y2 z2 dVdτ .
В результате простейших преобразований последнего равенства, получим
t t t t 2t 2t 2t
![]() τ wx
x wy
y wz
z c ρ
x2
y2
z2
,
p
τ wx
x wy
y wz
z c ρ
x2
y2
z2
,
p
либо
![]() t wx t wy t w t a t2 , z
t wx t wy t w t a t2 , z
τ x y z
где a – коэффициент температуропроводности.
Полученное уравнение является дифференциальным уравнением конвективного теплообмена, или уравнением Фурье-Кирхгофа. Оно выражает в наиболее общем виде распределение температур в движущемся потоке жидкости (газа).
Для твердых тел wx = wy = wz = 0 и уравнение
![]() t wx t wy t wz t a2t
t wx t wy t wz t a2t
τ x y z
превращается в дифференциальное уравнение теплопроводности
t 2t 2t 2t 2t 2t 2t
![]()
![]() cp
x2 y2 z2
a
x2 y2 z2 .
cp
x2 y2 z2
a
x2 y2 z2 .
t
При
установившемся процессе теплообмена ![]()
0, тогда
уравнение конвективного τ
0, тогда
уравнение конвективного τ
теплообмена для этого случая
![]() t t t 2 . wx wy wz a t
t t t 2 . wx wy wz a t
x y z
![]() t t t t 2 для практического
Ввиду сложности уравнения wx wy wz a t
t t t t 2 для практического
Ввиду сложности уравнения wx wy wz a t
τ x y z
использования его подобно преобразовывают с учетом условий однозначности, т.е. представляют в виде функции от критериев подобия. Для этого, с целью более полного описания конвективного переноса тепла, дифференциальное уравнение Фурье-Кирхгофа дополняется граничными условиями, вытекающими из закона теплообмена на границе твердого тела и окружающей его среды.
На практике процессы теплообмена осуществляются с помощью потоков разнообразных жидкостей и газов при различных режимах их движения в аппаратах различной геометрической формы и размеров. Однако условия подобия во всех случаях одинаковы и сводятся к подобию геометрических параметров, полей скоростей и температуры, а также физических констант. При этом должно соблюдаться подобие переноса тепла, как в пограничном слое, так и в ядре потока жидкости (газа).
Подобие переноса тепла в пограничном слое можно установить из краевых условий теплообмена на границе твердое тело – жидкость (газ), воспользовавшись зависимостью:
![]() F
t
F
t .
F
t
F
t .
т
Применив тот же метод подобного преобразования уравнений, что и при выводе критериев гидродинамического подобия, разделим правую часть последнего равенства на левую:
![]() F t т
т .
F t т
т .
F t
Заменив δт на характерный (определяющий) геометрический размер l, получим безразмерный комплекс величин, называемый критерием Нуссельта:
l
![]()
Nu
Nu
Критерий Нуссельта характеризует теплоперенос через пограничный слой в форме соотношения количества тепла, передаваемого конвекцией, и теплопроводностью.
Аналогом критерия Нуссельта при нестационарном теплообмене между твердым телом и жидкостью или газом является критерий Био:
l
Bi ![]() ,
,
где – коэффициент теплопроводности твердого тела.
Условия подобия в ядре потока определяются из уравнения Фурье-Кирхгофа. Для одномерного движения потока жидкости его можно представить в виде
t t 2t
![]() τ wx x a x2 .
τ wx x a x2 .
Поделив члены левой части на правую часть, отбросив знаки математических операторов и заменив величины x и wx на характерный геометрический размер l и осредненную скорость w соответственно, получим
t l 2 l2
![]() ; at a
; at a
twl2 wl
![]() . lat a
. lat a
![]()
![]() Полученный комплекс l
a2τ обычно
для удобства заменяют обратной величиной a lτ2
, которая выражает необходимое условие подобия неустановившихся
процессов теплообмена. Этот безразмерный комплекс получил название критерия
Фурье: aτ
Полученный комплекс l
a2τ обычно
для удобства заменяют обратной величиной a lτ2
, которая выражает необходимое условие подобия неустановившихся
процессов теплообмена. Этот безразмерный комплекс получил название критерия
Фурье: aτ
![]()
Fo . l2
Fo . l2
![]() Комплекс wl a является мерой
соотношения между теплом, переносимым конвекцией и теплопроводностью при
конвективном теплообмене, и носит название критерия Пекле:
Комплекс wl a является мерой
соотношения между теплом, переносимым конвекцией и теплопроводностью при
конвективном теплообмене, и носит название критерия Пекле:
wl
![]()
Pe.
Pe.
a
Необходимым условием теплового подобия являются предшествующие ему гидродинамическое и геометрическое подобия. Гидродинамическое подобие определяется критериями гомохронности Но, Рейнольдса Re и Фруда Fr, а геометрическое – постоянством отношений основных геометрических размеров поверхности (стенки) к некоторому характерному размеру L. В качестве характерного линейного размера для трубных поверхностей, которые часто используются в качестве теплопередающих, принимают диаметр трубы L = d, иногда – длину трубы L = l, радиус кривизны изогнутой трубы L = R и т.д. В результате критериальное уравнение конвективного теплообмена выражается функцией вида
![]() l1
; l2 ln ,
f
Nu,
Fo, Pe, Re, Fr, Ho, L L L
l1
; l2 ln ,
f
Nu,
Fo, Pe, Re, Fr, Ho, L L L
![]() l l1 ; 2 ln
– симплексы геометрического подобия.
l l1 ; 2 ln
– симплексы геометрического подобия.
где
L L L
Равенство критериев Нуссельта является следствием подобия геометрических и физических характеристик, а также подобия полей скоростей и температур. Поэтому Nu не является определяющим. В связи с этим обобщенную зависимость, описывающую кинетику переноса тепла в движущихся средах, представляют в виде
![]() l1
; l2 ln
.
l1
; l2 ln
.
Nu fFo, Pe, Re, Fr, Ho, L L L
Критерий Пекле обычно представляют в виде двух безразмерных комплексов
wl wl wlρ cpμ
![]() Pe
Re
Pr ,
a a
Pe
Re
Pr ,
a a
![]() где
где
![]() a
cp
Pr – критерий Прандтля,
характеризующий физические свойства теплоносителя (жидкости или газа).
a
cp
Pr – критерий Прандтля,
характеризующий физические свойства теплоносителя (жидкости или газа).
По физическому смыслу критерий Pr определяет соотношение полей скоростей и температур в потоке. Для капельных жидкостей он зависит от температуры (с повышением температуры увеличивается), а его численные значения лежат в пределах 3 ÷ 300. Для газов критерий Прандтля не зависит ни от температуры, ни от давления, являясь постоянной величиной для газов одинаковой атомности (для одноатомных газов Pr = 0,67; для двухатомных Pr = 0,72; для трехатомных Pr = 0,8; для четырехатомных и более Pr = 1).
С введением критерия Прандтля уравнение Nu принимает вид:
![]() l1
; l2 ln .
l1
; l2 ln .
Nu fFo, Pr, Re, Fr, Ho, L L L
При установившихся тепловых процессах и одинаковой геометрической форме потоков из уравнения Nu исключаются критерии Fo и Ho, содержащие время, и геометрические симплексы, тогда
Nu fPr, Re, Fr.
При рассмотрении конкретных задач теплообмена данное уравнение может быть видоизменено.
Так, при вынужденном движении, когда влияние сил тяжести на гидродинамику потока пренебрежительно мало, критерием Фруда можно пренебречь и критерий Нуссельта будет являться функцией лишь двух критериев:
Nu fRe, Pr.
При свободном движении жидкости (в условиях естественной конвекции) из критериального уравнения исключают критерий Рейнольдса:
Nu fPr, Fr.
Ввиду сложности определения скорости при естественной конвекции, входящей в критерий Фруда, последний заменяют производным критерием Архимеда, характеризующим естественную конвекцию, обусловленную разностью плотностей жидкости (газа) в различных точках потока:
![]() Ar
gl3
0 ,
Ar
gl3
0 ,
2 g
где ρ и ρ0 – плотности холодной и нагретой жидкости (газа).
![]() Поскольку в тепловых
процессах разность плотностей в различных точках системы обусловливается
разностью температур Δt нагретой и холодной жидкости, комплекс
0 в
критерии Архимеда целесообразно выразить через произведение Δt
( –
температурный коэффициент объемного расширения). Полученный новый критерий
является критерием Грасгофа:
Поскольку в тепловых
процессах разность плотностей в различных точках системы обусловливается
разностью температур Δt нагретой и холодной жидкости, комплекс
0 в
критерии Архимеда целесообразно выразить через произведение Δt
( –
температурный коэффициент объемного расширения). Полученный новый критерий
является критерием Грасгофа:
gl3
Gr ![]() t .
t .
2
Таким образом, критерий Gr представляет собой определяющий критерий теплового подобия при естественной конвекции, когда движение жидкости целиком обусловлено самим процессом теплообмена, а уравнение конвективного теплообмена для этого случая Nu fGr, Pr.
gl3
Для газов при Pr ≈ 1 уравнение Gr
![]() 2 t превращается в
функциональную зави-
2 t превращается в
функциональную зави-
симость критерия Нуссельта от критерия Грасгофа.
Помимо приведенных критериев теплового подобия в литературе часто встречаются производные критерии, составленные из указанных выше:
Nu
![]() критерий
Стантона St , RePr
w c p
критерий
Стантона St , RePr
w c p
который отражает соотношение количества тепла, передаваемого конвекцией, и тепла, переносимого движущимся потоком;
gl3
критерий Релея Ra Gr Pr ![]() t ;
t ;
![]() критерий
Грэтца Gz Pe
критерий
Грэтца Gz Pe ![]() d
Re Pr d
Gcp ,
d
Re Pr d
Gcp ,
l l l
(G – массовый расход жидкости) характеризует конвективный теплоперенос при ламинарном режиме.
Nucp fGz.
В соответствии с полученными критериальными уравнениями обрабатываются опытные данные по переносу тепла конвекцией и представляются в виде степенных уравнений.
Например, уравнение Nu fRe, Pr – в виде Nu ARe Prm n; уравнение
3
![]() gl m n
и т.д.
gl m n
и т.д.
Gr t – в виде Nu AGr Pr
2
При решении практических задач по найденному из соответствующего критериального уравнения значению критерия Нуссельта определяют коэффициент теплоотдачи:
Nu
![]() .
.
l
Критериальные зависимости в виде степенных уравнений, как уже указывалось, решают чисто эмпирически и применимы они лишь в тех пределах изменения аргумента, в которых подтверждены опытом. Поэтому области их надежного применения ограничены пределами, указываемыми в каждом отдельном случае. Ограничения эти, в основном, связаны с характером и режимом движения потока теплоносителя, его геометрической формой и размерами, изменением агрегатного состояния.
Разделение общего процесса переноса тепла на элементарные – теплопроводность, конвекцию и тепловое излучение – является лишь методическим приемом. В действительности эти явления протекают одновременно и, естественно, влияют друг на друга. Конвекция, например, всегда сопровождается теплопроводностью или лучеиспусканием; теплопроводность в пористых телах – конвекцией и лучеиспусканием в порах, а лучеиспускание – теплопроводностью и конвекцией.
В практических расчетах разделение таких сложных процессов на элементарные не всегда возможно и целесообразно. Обычно результат одновременного действия отдельных элементарных процессов приписывают одному из них, которое принимают главным. Влияние же остальных сказывается лишь на величине количественной характеристики основного.
Если теплообмен происходит между твердой стенкой и газообразной средой (например, воздухом), то тепло передается совместно конвекцией и излучением. Такой процесс переноса тепла получил название сложной теплоотдачи. Типичным примером сложной теплоотдачи являются потери тепла стенками аппаратов в окружающую среду.
Количество тепла, отдаваемое стенкой в единицу времени омывающему ее газу, за счет конвективного теплообмена составит Qк (tст t Fг ) , а за счет теплового излучения
![]() Тст
4 Т 4
Тст
4 Т 4
Qизл C1 2 100 100г F .
Если ввести обозначения
![]() изл C1
2 Тст
4
100Тг
4
,
изл C1
2 Тст
4
100Тг
4
,
100
tст tг
где изл – коэффициент теплоотдачи при лучеиспускании, то количество тепла, переданное излучением, выразится равенством
Qизл изл(tст t Fг ) .
Общее количество тепла, отданное стенкой в единицу времени, составит:
Q Qк Qизл ( изл )(tст t Fг ) ,
либо
Q прив ст(t t Fг) ,
где прив изл – приведенный коэффициент теплоотдачи, показывающий, какое количество тепла отдает 1 м2 стенки в окружающую среду в единицу времени при разности температур стенки и среды 1 С за счет конвективного теплообмена и теплового излучения.
В инженерных расчетах прив часто определяют приближенно по эмпирическим уравнениям. Например, при расчете тепла, теряемого наружной поверхностью аппаратов, находящихся в закрытых помещениях, в окружающую среду, прив можно рассчитать, пользуясь уравнением
прив 9,3 0,058tст.н ,
где tст.н – температура наружной поверхности стенки аппарата. Это уравнение при-
менимо в пределах изменения tст.н 50350 С.
Для уменьшения потерь тепла в окружающую среду аппараты и трубопроводы покрывают слоем тепловой изоляции.
Чтобы произвести приближенный расчет теплообмена, не располагая расчетными уравнениями и точными сведениями о значениях свойств веществ, а также оценить результаты расчетов, произведенных по теоретическим или эмпирическим формулам, необходимо располагать хотя бы приближенными значениями коэффициентов теплоотдачи. Ниже приводятся ориентировочные пределы значений коэффициентов теплоотдачи в промышленных теплообменных аппаратах.
|
При нагревании и охлаждении |
Вт/м2∙К |
|
- воздуха |
1,16 – 58 |
|
- псевдоожиженного слоя |
200 – 400 |
|
- перегретого пара |
23,2 – 116 |
|
- масел |
58 – 1740 |
|
- воды |
232 –11600 |
|
При кипении воды |
580 – 52200 |
|
При пленочной конденсации водяных паров |
4600 – 17400 |
|
При капельной конденсации водяных паров |
4600 – 140000 |
|
При конденсации паров органических жидкостей |
580 – 2320 |
Тема 3.3. Процессы теплопередачи
Процесс передачи теплоты от одной среды (теплоносителя) к другой среде (теплоносителю) через разделяющую их стенку называется теплопередачей и состоит из процессов теплоотдачи от горячего теплоносителя к поверхности стенки, передачи теплоты теплопроводностью через многослойную (или однослойную) стенку и процесса теплоотдачи от поверхности стенки к холодному теплоносителю. При установившемся процессе теплопередачи средние температуры горячего и холодного теплоносителей (сред) остаются постоянными вдоль поверхности стенки, а тепловой поток сохраняет неизменное значение (Q = const).
Расчетная формула стационарного процесса теплопередачи имеет следующий вид:
Q kFtср
где Q – тепловой поток; k – коэффициент теплопередачи; F – площадь поверхность
теплопередачи; tср = (tm1 – tm2) – средний температурный напор (средняя разность температур).
Коэффициент теплопередачи k выражает количество передаваемой теплоты в единицу времени через единицу площади поверхности при температурном напоре равном 1 градусу.
В большинстве случаев при движении теплообменивающихся жидкостей вдоль поверхности теплообмена их температуры изменяются. Коэффициент теплопередачи также изменяется по поверхности теплообмена.
Однако, во многих случаях можно рассматривать величину коэффициента теплопередачи постоянной по всей поверхности теплообмена, а разность температур между жидкостями принимать средней по поверхности теплообмена.
В этом случае для определения теплового потока имеем
Q ktdF
F
3.3.2. Теплопередача через плоскую однослойную и многослойную плоскую стенку
Рассмотрим процесс передачи теплоты через плоскую стенку (рис. 3.11.) поверхностью F, толщиной и коэффициентом теплопроводности . При известных температурах горячего tж1 и холодного теплоносителя tж2, а также коэффициентов теплоотдачи от горячего 1 и холодного 2 теплоносителей решение сводится к определению теплового потока, плотности теплового и температур внутренней и наружной поверхности стенки (граничные условия третьего рода). Принимая во внимание условие постоянства теплового потока можно записать ряд равенств
Q Q Q
![]() q1
q1 ![]() F 1tж1 tс1;
q2 F tc1 tc2;
q3
F 1tж1 tс1;
q2 F tc1 tc2;
q3 ![]() F1 tж2 tс2
F1 tж2 tс2
В этом ряду равенств первое уравнение определяет количество теплоты, передаваемой конвекцией (и излучением) от горячего теплоносителя к стенке; второе уравнение – то же количество теплоты, передаваемой теплопроводностью через стенку; третье уравнение – передачу того же самого количества теплоты, передаваемого конвекцией (и излучением) от стенки к холодному теплоносителю.
Рис. 3.11. Процесс передачи теплоты через плоскую стенку
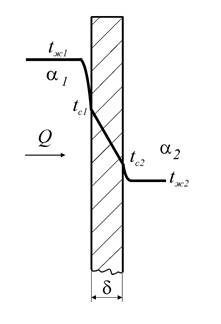
Выделим из этого ряда равенств разности температур
1 tж1 tc1 ![]() q1 R1q1; 1
q1 R1q1; 1
tc1 tc2 1 q2 R2q2;
1
1 tc2 tж2
![]() q3 R3q3.
q3 R3q3.
2
Складывая левые и правые части уравнений характеризующих разности температур и учитывая, что q q1 q2 q3 получим выражение для итоговой разности температур
tж1 tж2
![]() 11
11
11
11 ![]() 12 q R1 R2 R3 q Rq,
12 q R1 R2 R3 q Rq,
где R R1 R2 R3 – термическое сопротивление плоской стенки (м2 0С\Bm)
Отсюда, следует выражение для плотности теплового потока и теплового потока
(уравнение теплопередачи плоской стенки)
где q – плотность теплового потока (Вт/м2 ); Q – тепловой поток (Вт); k=1/R – коэффициентом теплопередачи плоской стенки (Вт/м2 ºС)
1 1 1
k ,
![]() R R1 R2 R3 1
1
R R1 R2 R3 1
1
1 2
где R R1 R2 R3 —термическое сопротивление теплопередачи плоской стенки (м2
ºС/Вт); R1 ![]() ; ;R2
; ;R2 ![]() ; R3
; R3 ![]() – термические сопротивления теплоотдачи со сто-
– термические сопротивления теплоотдачи со сто-
1 2
роны горячего теплоносителя, теплопроводности плоской стенки и термические сопротивления теплоотдачи со стороны холодного теплоносителя соответственно.
Температура внутренней и наружной поверхности стенки определяется из следующих соображений:
q ktж1 tж21tж1 tс12tс2 tж2
![]() tc1 tc2,
tc1 tc2,
отсюда имеем
1 1 1 1
![]()
![]() tс1 tж1 q
tс1 tж1 q ![]() tж2 q2
, tс2
tж2 q
tж2 q2
, tс2
tж2 q ![]() 2 tж1 q1
2 tж1 q1
1
В случае многослойной стенки, состоящей из п слоев (рис. 3.12.) тепловой поток и плотность теплового потока определяются по уравнениям аналогичным однослойной за исключением того, что термическое сопротивление и, следовательно, коэффициент теплопередачи определяются с учетом термических сопротивлений каждого слоя.
Рис. 3.12. Процесс теплопередачи многослойной плоской стенки
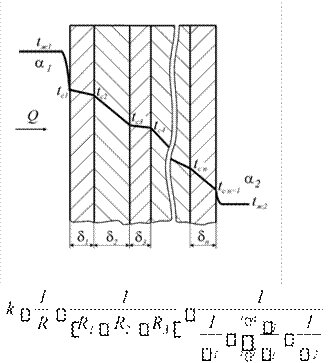
Температура поверхности и на стыке слоев определяется из тех же соображений, что и для однослойной стенки
1 i
![]() tci1
tж1 q1 1 ii
tci1
tж1 q1 1 ii
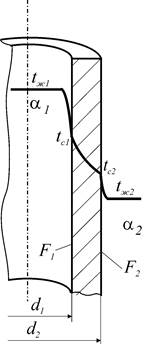
Для криволинейных стенок произведение kF
неразделимо и только для плоской стенки вследствие равенства F1 = Fm,i = F2 = F это произведение
распадается на k и F. Тогда для плоской стенки выражение
коэффициента теплопередачи запишется следующим образом; k ![]() .
.
![]()
1 i1 i 2
Для криволинейных стенок коэффициент теплопередачи принято определять по тому же уравнению, что и для плоской стенки. В этом случае для криволинейных стенок расчетная поверхность теплопередачи определяется из выражения
![]() 1 i 1
1 i 1
F n .
F1 i1 i Fm,i 2 F2
1
Удельная линейная плотность теплового потока ql для цилиндрической стенки (рис.
3.13.) в условиях теплопередачи является частным выражением основного уравнения
ql ![]() QL n t
t
t
ki ,
QL n t
t
t
ki ,
d1 i1 2i di 2di1 1
![]() где
Rl 1 kl — линейное
термическое сопротивление;
где
Rl 1 kl — линейное
термическое сопротивление;
1 n 1 ln di1 1 .
Rl
1d1 i1 2i di 2di1
Рис. 3.13. Процесс теплопередачи цилиндрической стенки
В технических расчетах чаще всего приходится решать проблему двух видов: уменьшение тепловых потерь (изоляция поверхности теплообмена) и увеличение количества передаваемого тепла (интенсификация теплопередачи).
1
Из выражения (Q ![]() t
kFt
qF )
следует, что чем больше q, тем R
t
kFt
qF )
следует, что чем больше q, тем R
больше тепловой поток, т. е. задача интенсификации теплообмена, сводится к увеличению удельного теплосъема. Увеличить q можно путем повышения ∆t и k. Увеличение ∆t может быть связано с изменением технологии процесса, что не всегда возможно; кроме того, увеличение ∆t всегда влечет возрастание энергетических затрат и повышение q в этих условиях в каждом конкретном случае решается на основе технико-экономических расчетов. Увеличить k можно за счет повышения коэффициентов теплоотдачи. При этом, как уже говорилось, при большом различии α1 и α2 коэффициент теплопередачи всегда меньше минимального α. Таким образом, увеличить k и интенсифицировать теплообмен можно двумя путями: при α1 << α2 или α2 << α1 — повышением меньшего коэффициента теплоотдачи; при α1 ≈ α2 — повышением обоих коэффициентов или любого из них.
Помимо увеличения коэффициентов теплоотдачи интенсифицировать процесс теплопередачи можно за счет оребрения поверхности теплоотдачи. Оребряется та поверхность, со стороны которой α меньше; теоретическим пределом оребрения является равенство термических сопротивлений теплоотдачи 1/( α1F1) = 1/(α2F2) в итоге увеличивается произведение kF и повышается Q.
В теплообменных аппаратах и теплоиспользующих устройствах температура греющего и нагреваемого теплоносителей изменяются вдоль поверхности теплообмена: температура греющего теплоносителя понижается, а температура нагреваемого повышается. Исключение составляют теплообменные аппараты, в которых с одной стороны поверхности испаряется жидкость или конденсируется пар (например испарители или конденсаторы).
В условиях изменяющихся температур теплоносителей уравнение теплопередачи для элементарной площади можно записать в следующем виде:
Тепловой поток передаваемый через всю поверхность теплообмена при постоянном коэффициенте теплопередачи k равен
Q k ti dF
F
Для учета изменения температур теплоносителей по поверхности теплообмена в расчетное уравнение теплопередачи вводится средняя разность температур (средний температурный напор), который определяется уравнением
1
m ![]() ti dFi
ti dFi
F F
где m – средняя разность температур.
Q kFm
Вид расчетного соотношения для средней разности температур существенно зави-
сит от взаимного направления, греющего и нагреваемого теплоносителей. Различают следующие направления движения теплоносителей в рекуперативных теплообменниках: прямоток, противоток, перекрестный ток, смешанный ток.
Рис. 3.14. Графики изменения температуры теплоносителей при прямотоке (а) и противотоке (б)
Пренебрегая падением давления теплоносителей при движении, т.е. считая процесс протекающим изобарным, из первого начала термодинамики имеем
Q Q1 Q2 G1 h1 G2 h2
где Q – мощность теплообменного аппарата, Вт; G1 и G2 – расход горячего и холодного теплоносителей соответственно, кг\с; h1 иh2 – изменение удельной энтальпии греющего и нагреваемого теплоносителей соответственно, Дж\кг.
Для конвективных теплообменных аппаратов (в процессе теплообмена отсутствуют
фазовые переходы) в силу того, что
h cpmt имеем
Q Q1 Q2 G1 cpm1 t1
В силу того, что для теоретического процесса теплопередачи в ТА, тепловой поток, определенный из уравнение теплового баланса равен тепловому потоку, определенному по уравнению теплопередачи, имеем
Расчетные соотношения для определения средней разности температур простейших схем взаимного движения теплоносителя: прямотока и противотока получаются из выражения, записанного для элементарного участка теплообмена
Q dkF W1dt1 W2 dt2
dt1 ![]() Q; dt2
Q; dt2 ![]() Q
Q
W1 W2
1 1 1 1 1 1
![]()
![]() dt1 dt2 dW1 m W2 Q W
dt1 dt2 dW1 m W2 Q W![]() m Q; Wm W1 W2
m Q; Wm W1 W2
Q Wmd dkF
![]() kF 1 kF 1
2
kF 1 kF 1
2
![]()
ln
ln ![]() W
W
Wm 2 m m
Расчетное уравнение средней разности температур справедливое для схем прямотока и противотока, называется среднелогарифмической разностью температур или уравнением Грасгофа.
![]() m ml 1 2 ln 1 2
m ml 1 2 ln 1 2
для схемы прямоток 1 t1 t2 ; 2 t1 t2
для схемы противоток 1 t1 t2 ; 2 t1t2
Согласно графоаналитическому методу, предварительно по формуле Грасгофа подсчитывается среднелогарифмическая разность температур для противоточного теплообменного аппарата.
Затем с учетом схемы движения теплоносителей (число ходов по трубному и межтрубному пространству) из графиков определяется коэффициент t =f(PS и R)
![]()
![]() R (t1
t1) W2 ; PS (t2
t2 ); m t mL
R (t1
t1) W2 ; PS (t2
t2 ); m t mL
(t2 t2 ) W1 (t1 t2 )
Николай Белоконь[29] предложил обобщенное уравнение для определения средней разности температур справедливое для любых схем движения теплоносителей
m ![]() I II ; II
ma 0,5T I
ma 0,5T;
I II ; II
ma 0,5T I
ma 0,5T;
II
- характеристическая разность температур,
Wm – приведенный водяной эквивалент теплоносителей,
![]() 1 ( 1
1 2 4 p
1 ( 1
1 2 4 p
)
Wm W1 W2 W1W2
Индекс противоточности р определяется как отношение водяного эквивалента поверхности теплообмена, где осуществляется противоточная схема движения теплоносителей (kF)прот, и водяного эквивалента поверхности теплообмена всего ТА (kF)
(kF)прот (kF)прот
![]() p (kF) [(kF)прот (kF)прям]
p (kF) [(kF)прот (kF)прям]
Для прямоточной схемы индекс противоточности равен p = 0, а при противотоке p =
1 и в этом случае уравнение уравнение Белоконя совпадает с уравнением Грасгофа[30].
3.3.6. Расчет теплообменный аппаратов первого рода
При конструкторском тепловом расчете известны: вид теплоносителя, температура теплоносителей на входе и выходе из теплообменного аппарата, а также расходы теплоносителей. Определяют тепловую мощность и площадь поверхности теплообменного аппарата (ТА), с дальнейшим конструированием нового или выбором стандартного аппарата.
В основу теплового расчета рекуперативных ТА положены: уравнение теплового баланса и обобщенное уравнение теплопередачи при переменных температурах
На первом этапе определяется мощность теплообменного аппарата из теплового баланса. Рассчитывается коэффициент теплопередачи К
1
![]() k 1 in i 1 ,
k 1 in i 1 ,
1 i1 i 2
коэффициенты теплоотдачи, а также значения термических сопротивлений загрязне-
ний и стенки теплообменной трубы находятся по справочной литературе.
Конструируемый или выбираемый стандартный теплообменный аппарат способен обеспечить заданные температурные режимы теплоносителей, если его индекс противоточности при заданных температурных режимах и водяных эквивалентах теплоносителей больше или равен минимальному индексу противоточности pmin
Определяется средняя разность температур для выбранной схемы
![]() m I II ;
m I II ;
II
определяется расчетная площадь поверхности теплообмена
Q
![]()
Fр K m
Затем оцениваются площади проходных сечений трубного и межтрубного пространства (при условии достижения оптимальных скоростей движения теплоносителей)
G f ![]() w
w
На базе полученных расчетных значениях площади теплообмена и проходных сечений либо определяются расчетным путем геометрической характеристики теплообменного аппарата (число ходов, диаметр, длина, количество, схема расположения трубок, число сегментных перегородок и т. д.) либо из каталога выбирается стандартный теплообменный аппарат
3.3.7. Расчет теплообменный аппаратов второго рода
Известно: W1, W2, G1, G2, t1, t2 , F , l.
Найти: t1, t2, Q.
Проверка расчётов второго рода.
Дано: геометрия, F , W1, W2, t1, t2 , K (из расчётов первого рода).
Найти: t1 и t2.
Решение: В случае если K не дано, то его модно найти по формуле:
1
![]() K 1 n i 1
K 1 n i 1
1 i1 i 2
Из логических соображений зададимся температурами t1 и t2,тогда
Q W1t1 W2t2 ,
Q Q
где t1 t1 t1 W![]() 1 , t2 t2 t2 W
1 , t2 t2 t2 W![]() 2 .
2 .
Используя метод Белоконя, получим следующее уравнение:
Q 2t1 t2
 1 2 m
1 2 m
e m 1
2
1 1 1 4P
![]() Wm W1 W2
W1W2
Wm W1 W2
W1W2
3.3.8. Паросиловые установки, цикл Ренкина, методы повышения КПД.
Паросиловые установки (циклы):
a. Объекты, производящие тепловую энергию.
b. Объекты, производящие работу.
c. Цикл Карно (рабочее тело – конденсирующий газ).
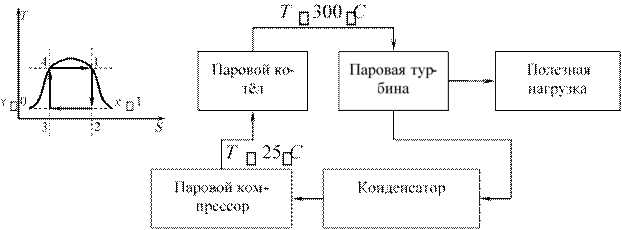
Рис. 3.15. Цикл Ренкина паросиловых установок
Паровые котлы бывают двух типов: прямоточного типа и барабанного типа. T2
t 1
T1
Удельная работа в турбине hт .
Удельная работа в компрессоре hк .
Полезная удельная работа hт hк .
hт hк
Эффективный коэффициент полезного действия системы: e ![]() .
q
.
q
e tiотм ,
где iот – относительный индикаторный коэффициент полезного действия, tiот i – индикаторный внутренний коэффициент полезного действия,
м – механический коэффициент полезного действия.
Цикл Ренкина – идеальный цикл для паросильных установок.
Вместо компрессора устанавливают насос и пароперегреватель. lт h1 h2 lн VP1 P2 , где V – объём жидкости. Пренебрегая работой насоса, получим: q h1 h3
lт lн h1 h2 h1 h2 h1 h2
t ![]()
![]() , q h1 h3 h1
h2 h1 Cptк
, q h1 h3 h1
h2 h1 Cptк
где tк – температура конденсации.
Для увеличения эффективности надо одновременно увеличивать давление и температуры перегрева.
где Ne – эффективная мощность турбины, B – расход топлива, Q – теплотворная
способность.
Существует два пути повышения экономичности паросиловой установки:
1. повышение параметров пара перед турбиной
2. усложнение схем паросиловых установок
Эффективность может повысить дальнейшее использование теплоты отработавшего пара.
3.3.9. Воздушные холодильные машины
Холодильные установки предназначены для охлаждения тел до температуры ниже температуры окружающей среды. Чтобы осуществить такой процесс, необходимо от тела отвести теплоту и передать ее в окружающую среду за счет работы, подводимой извне.
![]() 2
2
T1
Рис. 3.15. Цикл Карно
Цикл Карно:
S1 – работа цикла.
S2 S1 q1 ;
![]() q2 x
q2 x
lцикла ;
Холодильные машины бывают следующих видов:
1. Парокомпрессионные холодильные машины, в которых рабочим телом является пар, а рабочий процесс протекает в компрессоре.
2. Воздушные холодильные машины, в которых рабочим телом является воздух.
3. Абсорбционные холодильные машины, в которых идёт поглощение паров водными растворами.
4. Пароструйные холодильные машины, имеющие инжекторы в качестве исполнительного механизма.
Воздушная холодильная установка
Для более глубокого охлаждения тел (получения более глубокого холода) используется воздушная холодильная установка (рис.).
Принцип действия воздушной холодильной установки основан на расширении предварительно сжатого и охлажденного воздуха. Воздух из холодильной камеры (4) под давлением p1 поступает в компрессор (1), где адиабатно сжимается (1–2) до давления p2 и температуре T2. Сжатый воздух подается в теплообменник (2), где охлаждается проточной водой до температуры T3 (2–3), и подается в турбодетандер (3), где адиабатно расширяется (3–4) до давления p1, при этом температура рабочего тела понижается до значения T4. Охлажденный воздух поступает в холодильную камеру, где нагревается до температуры T1 (4–1).
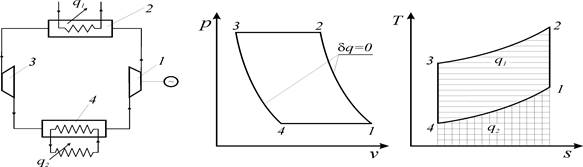
Рис. 3.17. Схема, p-v и T-s диаграммы воздушной холодильной установки
Удельное количество теплоты, переданное охлаждающей воде, может быть определено по соотношению
![]() q1 cpm T2 T3,
q1 cpm T2 T3,
удельное количество теплоты, отведенное от воздуха в холодильной камере, по фор-
муле
![]() q2 cpmT1 T4,
q2 cpmT1 T4,
а удельная работа цикла при условии постоянства теплоемкости рабочего тела ( cpm idem) может быть рассчитана из выражения
![]() lц l1,2 l3,4 q1 q2 cpm T2 T3 T1 T4
lц l1,2 l3,4 q1 q2 cpm T2 T3 T1 T4
или, поскольку для адиабатных процессов (1–2) и (3–4) справедливы следующие соотношения температур:
T1![]() T2 T4
T2 T4![]() T3 ; T1
T3 ; T1![]() T4 T2
T4 T2![]() T3 ,
T3 ,
T3 )
определена по формуле lц cpm (T2 T1 )(1
T2
При использовании данных соотношений холодильный коэффициент воздушной холодильной может быть определен из формулы
![]()
![]() T3 )] T1 .
T3 )] T1 .
t q2lц (T1 T4 )/[(T2 T1 )(1
T2 T2 T1
3.3.10. Рабочий процесс двухтактного и четырехтактного двигателя внутреннего сгорания
Для того, чтобы превратить теплоту в работу нужно совершить какой-то процесс (цикл).
q
![]() P ab - сжатие. bcd - подвод теплоты.
P ab - сжатие. bcd - подвод теплоты.
d e - расширение. a ea - отвод теплоты.
ab - сжатие.
bc - подвод теплоты. P
cd - расширение. b d a - отвод теплоты.
Рис. 3.18. Цикл со смешанным v подводом теплоты:
(а) цикл Сабате-Тринклера, (b) цикл Отто
Внутренняя (внешняя) мёртвая точка, наружная мёртвая точка – крайние положения поршня.
Ход поршня – движение от внутренней мёртвой точки до наружной мёртвой точки.
Такт – часть рабочего процесса, приходящаяся на один ход поршня.
Двигатели внутреннего сгорания бывают следующих видов:
1. Двухтактные двигатели внутреннего сгорания.
2. Четырёхтактные двигатели внутреннего сгорания. p0 – давление, под которым в камеру поступает заряд. Точка a – точка закрытия впускающего клапана.
Коэффициент заполнения v – отношение действительного количества заряда по массе к теоретическому количеству заряда, которое могло поступить при данных условиях,
![]() Gдейств 1.
Gдейств 1.
то есть v Gтеор
bcd – процесс сгорания в дизельном двигателе.
Точка c – момент проскакивания искры между электродами свечи в карбюраторном двигателе.
Точка e – точка открытия выпускного клапана. Точка g – точка открытия впускного клапана.
Точка h – точка закрытия выпускного клапана.
Рабочий процесс.
Первый такт – такт всасывания h k. Во время этого такта происходит окончание выхлопа h j и наполнение камеры сгорания зарядом h k.
Второй такт – такт сжатия k b. Во время этого такта происходит конец наполнения камеры сгорания зарядом k a и сжатие заряда a b. В конце процесса сжатия заряда, его температура повышается до какой-то Tb . Для дизельных двигателей эта температура должна быть больше температуры возгорания, то есть Tb Tвозг , а для карбюраторных двигателей она должна быть меньше температуры возгорания, то есть Tи Tвозг .
Третий такт – рабочий такт b f , такт расширения. Во время этого такта происходит сгорание заряда (bcd для дизельных двигателей и cd для карбюраторных двигателей), расширение заряда b f и начинается выпуск e f .
Четвёртый такт – выхлоп, такт очистки f h. Во время этого такта идёт выпуск f h и начинается наполнение камеры сгорания зарядом g h.
Первый и четвёртый такты являются процессами газообмена. Это вспомогательные такты. Вследствие отсутствия в них термодинамики, они являются вредными.
[1] Леонардо Эйлер (1707-1783), академик Петербургской академии наук. Автор работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям.
[2] Блез Паскаль (1623-1662) французский математик, физик, религиозный философ и писатель. Сформулировал одну из основных теорем проективной геометрии и основной закон гидростатики.
[3] Пьер Вариньон (1654-1772) французский механик и математик, член Парижской АН. Теорема Вариньона: если система сил сил Fi имеет равнодействующую R, то момент Мо (Fi) равнодействующей относительно любого центра О (или оси z) равен сумме моментов Mo (Fi) составляющих сил относительно того же центра О (или той же оси z).
[4] Жозеф Луи Лагранж (1736-1813), французский математик и механик, член Парижской АН. Установил фундаментальный «принцип возможных перемещений» и завершил математизацию механики. Внёс огромный вклад в математический анализ, теорию чисел, в теорию вероятностей и численные методы, создал вариационное исчисление.
[5] Даниил Бернулли (1700-1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики.
[6] Юлиус Людвиг Вейсбах (1806-1871), саксонский математик и механик-гидравлик. Вывел эмпирическую формулу, определяющую потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях.
[7] Жан Шарль Борда (1733-1799), французский физик и геодезист. Член Парижской АН. Участвовал в разработке метрической системы мер. Предложил особую насадку, названную его именем, для увеличения расхода жидкости, вытекающей из сосуда, при заданном сечении выходного отверстия. Доказал носящую его имя теорему в гидравлике об ударе струи жидкости или газа.
[8] Осборн Рейнольдс (1842-1912), английский механик, физик и инженер, специалист в области гидромеханики и гидравлики. Экспериментально установил критерий перехода ламинарного режима движения жидкости, текущей в цилиндрической трубе, в турбулентный режим.
[9] Жан Луи Мари Пуазёйль (1799-1869), французский врач и физик, экспериментально установил закон истечения жидкости через тонкую цилиндрическую трубку.
[10] Джованни Баттиста Вентури (1746-1822), итальянский учёный, известен работами в области гидравлики, теории света и оптики. Его именем названы открытый им эффект понижения давления газа или жидкости с увеличением скорости их движения, а также труба Вентури.
[11] Николай Егорович Жуковский (1847-1921) русский ученый, основоположник современной гидро- и аэромеханики.
[12] Роберт Гук (1635-1703), английский естествоиспытатель и изобретатель. Считается отцом экспериментальной физики. Сформулировал закон пропорциональности между силой, приложенной к упругому телу, и его деформацией.
[13] Бенуа Поль Эмиль Клапейрон (1799-1864) французский физик и инженер, вывел уравнение состояния идеального газа, объединяющее закон Бойля-Мариотта, закон Гей-Люссака и закон Авогадро, обобщённое в 1874 году Д.И. Менделеевым.
[14] Джозайя Уиллард Гиббс (1839-1903), американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.
[15] Рудольф Юлиус Эмануэль Клаузиус (1822-1888), немецкий физик, механик и математик, известен работами по упругости тел, по оптике и динамическому электричеству, а также формулировкой второго закона термодинамики.
[16] Макс Карл Эрнст Людвиг Планк (1858-1947), немецкий физик-теоретик, основоположник квантовой физики, лауреат Нобелевской премии по физике, сформулировал второе начало термодинамики в виде принципа возрастания энтропии и использовал его для решения различных задач физической химии.
[17] Юлиус Роберт фон Майер (1814-1878), немецкий медик и естествоиспытатель, указал на эквивалентность затрачиваемой работы и производимого тепла и тем обосновал первый закон термодинамики; он же впервые рассчитал, исходя из теоретических оснований, механический эквивалент тепла.
[18] Симеон Дени Пуассон (1781-1840), французский математик, механик и физик, определил величину отношения относительного поперечного сжатия к относительному продольному растяжению характеризущюю упругие свойства изотропных материалов.
[19] Йоханнес Дидерик Ван дер Ваальс (1837-1923), голландский физик, лауреат Нобелевской премии по физике, исследовал поведение молекул и занимался теориями, описывающими состояния материи, вывел уравнение состояния, показавшее, что при некоторой температуре исчезают различия в физических свойствах жидкости и её пара, находящихся в равновесии.
[20] Николя Леонар Сади Карно (1786-1832), французский физик и математик, вывел основные понятия термодинамики: идеальная тепловая машина, идеальный цикл, обратимость и необратимость термодинамических процессов.
[21] Карл Густав Патрик де Лаваль (1845-1913), шведский инженер и изобретатель, изобрёл сопло, служащее для подачи пара в турбину, получившее впоследствии его имя, и использующееся в том же назначении по настоящее время.
[22] Уильям Джон Макуорн Ранкин (1820-1872), шотландский инженер, физик и механик, один из создателей технической термодинамики, получил общие уравнения термодинамики, выражающие соотношение между количеством теплоты и механической энергией, построил полную теорию паровой машины; в частности, разработал идеальный термодинамический цикл парового двигателя.
[23] Жан-Батист Жозеф Фурье (1768-1830), французский математик и физик, открыл термоэлектрический эффект, доказал теорему о числе действительных корней алгебраического уравнения, лежащих между данными пределами, вывел уравнения теплопроводности в твёрдом теле, и разработал методы его интегрирования при различных граничных условиях.
[24] Людвиг Больцман (1844-1906), австрийский физик-теоретик, основатель статистической механики и молекулярно-кинетической теории, вывел закон для испускательной способности абсолютно чёрного тела с учётом пропорциональности давления равновесного излучения.
[25] Йозеф Стефан (1835-1893), австрийско-словенский физик и математик, путём измерения теплоотдачи платиновой проволоки при различных температурах установил пропорциональность излучаемой ею энергии четвёртой степени абсолютной температуры.
[26] Густав Роберт Кирхгоф (1824-1887), немецкий физик, иностранный член-корреспондент Петербургской АН, заложил основы спектрального анализа, открыл цезий и рубидий, ввел понятие абсолютно черного тела и открыл закон излучения, названный его именем.
[27] Иоганн Генрих Ламберт (1728-1777), немецкий физик, философ, математик и астроном, один из родоначальников современной математической логики, развил теорию отражения света матовыми поверхностями, ввел в науку термин «альбедо», доказал иррациональность чисел π и e, ввел понятие двойных звезд, выдвинул идею иерархического строения Вселенной.
[28] Георг Вильгельм Рихман (1711-1753), российский физик, вывел носящую его имя формулу для определения температуры смеси однородных жидкостей, имеющих разные температуры, проводил опыты по теплообмену и испарению жидкостей в различных условиях, предложил первую работающую модель электроскопа со шкалой.
[29] Николай Иович Белоконь (1899-1970), выдающийся советский учёный в области термодинамики, теплотехники, энергетики железнодорожного транспорта и транспорта нефти и газа, обобщил математическое выражение первого начала термодинамики для обратимых и необратимых процессов, введя понятие внутреннего теплообмена, дал независимое (от принципа необратимости) обоснование принципа существования энтропии, впервые ввёл в расчётные схемы теплопередачи индекс противоточности.
[30] Франц Грасгоф (1826-1893), немецкий механик и машиностроитель, развил учение о кинематических парах и кинематических цепях, разработал теорию регуляторов, вычислил критерий подобия, определяющий процесс теплообмена при свободном движении в поле гравитации и являющийся мерой соотношения архимедовой (подъёмной) силы, вызванной неравномерным распределением плотности в неоднородном поле температур, и сил межмолекулярного трения.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.