Яковлева Татьяна Петровна,
доцент кафедры математики и физики
Камчатского государственного университета имени Витуса Беринга,
кандидат педагогических наук, доцент,
г. Петропавловск – Камчатский,
Камчатский край
Тест по теме «Теория вероятностей»
1. Выберите случайные события A:
а) А – выбор черного шара из урны с белыми шарами.
б) А – выбор белого шара из урны с белыми шарами.
в) А – выпадение 6 очков при выбрасывании игральной кости.
г) А – выбор белого шара из урны с черными шарами.
2. Вероятность наступления некоторого события не может быть равна…
а) 19.
б) 0.
в) 1.
г) 0,9.
3. Два одноклассника поступают в институт на разные факультеты. Первый одноклассник поступит с вероятностью 0,5; второй – с вероятностью 0,6. Тогда вероятность того, что оба одноклассника поступят, равна…
а) 0,03.
б) 0,3.
в) 0,7.
г) 1,1.
4. В ящике 20 качественных и 5 бракованных деталей. Опыт состоит в выборе только одной детали. Событие А – «вынули качественную деталь». Событие В – «вынули бракованную деталь». Тогда для этих событий верным будет утверждение:
а) «Вероятность события А больше, чем вероятность события В».
б) «Вероятность события А равна 
».
в) «Событие В невозможно».
г) «Событие А достоверно».
5. Укажите рисунок, на котором изображен график плотности вероятностей для нормального распределения (рис. 1):
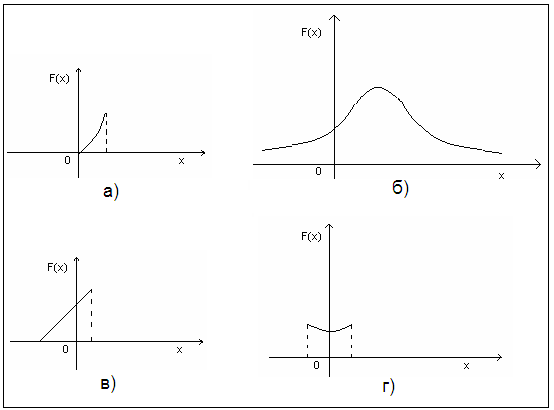
Рис. 1.
6. Для вычисления математического ожидания дискретной случайной величины используется формула …
а) 
.
б) 
.
в) 
.
г) 
.
7. Вероятность наступления некоторого события не может быть равна…
а) – 0,4.
б) 1.
в) 0.
г) 4.
8. Дискретная случайная величина Х имеет закон распределения вероятностей (табл. 1):
Таблица 1
|
Х |
2 |
6 |
|
Р |
0,3 |
0,7 |
Тогда математическое ожидание M(X) этой случайной величины равно…
а) 3,2.
б) 4,8.
в) 8.
г) 1.
9. Выберите невозможные события:
а) А – «замерзание воды в реке при температуре +30°С».
б) А – «выпадение 6 очков при подбрасывании игральной кости».
в) А – «наступление лета после весны».
г) А – «выбор черного шара из урны с белыми шарами».
10. Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет чётное число очков, меньшее 6, равна …
а)
.
б)
.
в)
.
г)
.
д)
.
11. Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет нечётное число очков, не меньшее 3, равна …
а)
.
б)
.
в) 1.
г)
.
д)
.
12. Установить соответствие между частями формул а), б), в), г) и 1), 2), 3), 4):
|
а) Р(А+В) = |
1) М(Х) |
|
б) Р(А)+Р( |
2) Р(А)+Р(В) |
|
в) |
3) |
|
г) |
4) 1 |
|
|
|
13. Какие из следующих событий достоверные:
а) А – «наугад выбранное трехзначное число меньше 1000».
б) В – «появление не более 18 очков при бросании трех игральных костей».
в) С – «два попадания при трех выстрелах».
Ответы к тесту
1. в).
2. а).
3. б).
4. а).
5. б).
6. а).
7. а), г).
8. б).
9. а), г).
10. в).
11. а).
12. а) – 2); б) – 4); в – 1); г) – 3).
13. а), б).
Яковлева Татьяна Петровна , доцент кафедры математики и физики
В ящике 20 качественных и 5 бракованных деталей
Для вычисления математического ожидания дискретной случайной величины используется формула … а)
Выберите невозможные события: а)
Установить соответствие между частями формул а), б), в), г) и 1), 2), 3), 4): а)
Ответы к тесту 1. в)
© ООО «Знанио»
С вами с 2009 года.
