
Тема: «Тригонометрические тождества.».
Часть 1. Заполните пропуски, чтобы получилось верное утверждение или правило.
Вариант 1.
1. Синусом угла α называется … точки, полученной поворотом точки
(1 ; 0) вокруг начала координат на угол α.
2. Котангенсом угла α называется отношение … угла к его ….
3. Если sin ɑ < 0, а cos ɑ > 0, то угол находится в … четверти.
4. Если sin ɑ > 0, а ctg ɑ < 0, то угол находится в … четверти.
5. Справедливы следующие равенства:
Sin ( - ɑ) = … , tg ( - ɑ) = … .
6. Справедливы следующие равенства:
Cos (2π±ɑ) =… , tg(π±ɑ) = … .
7. Основное тригонометрическое тождество
… + … = 1 выполняется при любых значениях ɑ.
8. Следствием из основного тригонометрического тождества является формула, выражающая синус через косинус:
sin ɑ= … .
9. Тангенсом угла ɑ называется отношение … угла ɑ к … этого угла.
10.Формула ctg
ɑ=
![]() не
имеет смысла при ɑ =… .
не
имеет смысла при ɑ =… .
11.Формула, связывающая тангенс угла ɑ с котангенсом этого угла имеет вид … .
12. Из этой формулы tg = … .
13. 1 + ctg 2 ɑ = … .
14. Синус угла ɑ … ( может или не может)
принимать значение 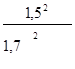
Часть 1. Заполните пропуски, чтобы получилось верное утверждение или правило.
Вариант 2.
1 .Косинусом угла α называется … точки, полученной поворотом точки
(1 ; 0) вокруг начала координат на угол α.
2. Тангенсом угла α называется отношение … угла ɑ к его ….
3. Если sin ɑ > 0, а cos ɑ < 0, то угол находится в … четверти.
4. Если cos ɑ > 0, а tg ɑ < 0, то угол находится в … четверти.
5. Справедливы следующие равенства:
cos( - ɑ) = … , tg ( - ɑ) = … .
6. Справедливы следующие равенства:
sin (2π±ɑ) =… , ctg(π±ɑ) = … .
7. Основное тригонометрическое тождество
… + … = 1 выполняется при … .
8. Следствием из основного тригонометрического тождества является формула, выражающая косинус через синус:
cos ɑ= … .
9.Котангенсом угла ɑ называется отношение … угла ɑ к … этого угла.
10.Формула tg
ɑ=
![]() не
имеет смысла при ɑ =… .
не
имеет смысла при ɑ =… .
11.Формула, связывающая котангенс угла ɑ с тангенсом этого угла имеет вид … .
12. Из этой формулы сtg = … .
13. 1 + tg 2 ɑ = … .
14.
Синус и косинус угла ɑ … (
могут или не могут) принимать значение 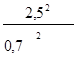 .
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.