Данный сборник состоит из двух частей. Первая часть: Задачи и решения XXII осеннего турнира по математике и информатике «Черноризец Храбр». В этой части приводятся задачи с решениями для школьников 2-12 классов. Вторая часть: Материалы по подготовке к турниру «Черноризец Храбр» и другим математическим состязаниям и конкурсам. Она содержит задачи для школьников 7-8 классов. Приведенные задачи также будут полезны и школьникам старших классов. Сборник рассчитан на широкий круг читателей, интересующихся математикой.

Б. ЛАЗАРОВ

Е.В. МИХАЙЛОВ

Турнир по математике и информатике

Задачи, решения, материалы для подготовки

Б. Лазаров, Е.В. Михайлов

Турнир по математике и информатике

ЧЕРНОРИЗЕЦ ХРАБР

ЗАДАЧИ, РЕШЕНИЯ,

МАТЕРИАЛЫ ДЛЯ ПОДГОТОВКИ

Архангельск

Издательство «КИРА»

2015

УДК 373.5(082)

ББК 74.261.6я43+74.262.21я43

Л 17

Авторы: Б. Лазаров, Е.В. Михайлов

Рецензенты: доктор педагогических наук, профессор, профессор кафедры экспериментальной математики и информатизации образования Северного (Арктического) федерального университета имени М. В. Ломоносова М. В. Шабанова; доцент Северного (Арктического) федерального университета имени М. В. Ломоносова В. В. Тепляков

Лазаров, Борислав.

Л 17 «Черноризец Храбр» : турнир по математике и информатике :

задачи, решения, материалы для подготовки / Б. Лазаров, Е. В.

Михайлов. – Архангельск : КИРА, 2015. – 110 с. : рис.

ISBN 978-5-98450-372-3.

Агентство CIP Архангельской ОНБ

Сборник рассчитан на широкий круг читателей, интересующихся математикой.

УДК 373.5(082)

ББК 74.261.6я43+74.262.21я43

ISBN 978-5-98450-372-3 © Лазаров Б., Михайлов Е. В., 2015

Предисловие

Учредителем турнира «Черноризец Храбр» является Институт математики и информатики Болгарской академии наук. Впервые

турнир был проведен в 1992 г.

По традиции в Болгарии турнир «Черноризец Храбр» проводится 1 ноября в рамках празднования национального болгарского праздника «День Болгарских просветителей». К числу почитаемых в Болгарии просветителей относится и Черноризец Храбр. Учредители математического турнира дали турниру его имя в связи с тем, что в своем «Сказании о Письменах» Черноризец Храбр описал ис-

торию зарождения цифровой записи чисел в Болгарии.

Данный сборник состоит из двух частей: Задачи и решения XXII осеннего турнира по математике и информатике «Черноризец

Храбр»; Материалы по подготовке к математическому турниру «Черноризец Храбр» и другим математическим состязаниям и

конкурсам.

Первая часть сборника написана Бориславом Лазоровым. Пере-

вод с болгарского выполнил Е. В. Михайлов.

Вторая часть сборника составлена Е. В. Михайловым. В ней приводятся материалы занятий со школьниками 7–8 классов для подготовки к турниру «Черноризец Храбр» и другим математическим состязаниям и конкурсам. Данные задачи могут быть полезны и школьникам старших классов. Задачи разбиты на 7 тем. Внутри темы задачи, как правило, расположены по возрастанию сложности решения. К большинству задач приведены решения или указания. Однако авторы не рекомендуют сразу заглядывать в них. Решение многих задач требует длительных размышлений и оригинальных

идей.

Решение школьной задачи является для ученика маленьким научным открытием. И если задача заставила быть изобретательным, придумывать что-то новое, то радость от ее самостоятельного решения должна быть ОГРОМНОЙ. Если через некоторое время Вам все-таки не удалось найти решение, не огорчайтесь, постарайтесь разобрать решение, которое приведено после списка задач в каждой

теме.

Задачи и решения XXII осеннего турнира по математике и информатике «Черноризец Храбр»

Инструкция для 2 класса

1. Время работы 60 минут. Не разрешается использование калькуляторов и другой вычислительной техники.

2. К каждой задаче приведено 5 возможных ответов. В бланке ответов за номером задачи буквой А, Б, В, Г или Д отметьте тот ответ, который Вы считаете верным.

3. Пишите разборчиво ЗАГЛАВНЫМИ ПЕЧАТНЫМИ буквами. Неоднозначно или нечетко указанный ответ может быть сочтен ошибочным. Если Вы не уверены какой ответ дать, то

можете соответствующее поле не заполнять, т.е. оставить поле за номером задачи пустым.

Начисление очков:

• правильный ответ к каждой задаче — 7 очков;

• неуказанный ответ к задаче — 3 очка;

• неверный ответ — 0 очков.

Задачи для 2 класса

1.Чему равно 20 − 1 − 3?

А) 7 Б) 10 В) 16 Г) 20 Д) ни одно из перечисленных

2.18 − 16 + 14 − 12 + 10 − 8 + 6 − 4 + 2 =

А) 12 Б) 10 В) 8 Г) 6 Д) ни одно из перечисленных

3.Какие значения принимают числа A и B на схеме A −+3→ 12 −−→5 B ?

А) A = 2, B = 7

Б) A = 8, B = 6

В) A = 9, B = 7

Г) A = 5, B = 9

Д) A = 3, B = 6

4.Каждую ночь г-жа Фета худеет на 1кг. На сколько килограммов похудела госпожа с обеда понедельника прошлой недели к обеду пятницы этой недели?

А) 10 Б) 11 В) 12 Г) 13 Д) ни одно из перечисленных

5.Натуральные числа от 1 до 20 выписаны в строчку:

1234567891011...1920. Сколько раз записана цифра 1?

А) 10 Б) 11 В) 12 Г) 13 Д) ни одно из перечисленных

6.Каждый лестничный пролет между соседними этажами жилого дома имеет 22 ступени. На сколько ступеней нужно Ачо подняться с третьего этажа, чтобы оказаться у своего друга Чочо на седьмом этаже?

А) 110 Б) 99 В) 88 Г) 77 Д) 66

7.Сколько имеется двузначных чисел, в которых встречается цифра 1, но нет цифры 2?

А) 9 Б) 11 В) 16 Г) 17 Д) 19

8.В поезде 10 вагонов. Иво находится в пятом вагоне, если считать от начала поезда. Поли едет на один вагон перед Иво. Если считать с конца поезда, в каком вагоне находится Поли?

А) 3 Б) 4 В) 5 Г) 6 Д) 7

9.Сколько всего квадратов на рисун-

ке?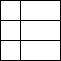

А) 4 Б) 5 В) 6 Г) 7 Д) 8

10. Если раздать 19 яблок 12 ребятам, так чтобы каждый получил по меньшей мере по одному яблоку, то какое наибольшее число яблок может получить один из них?

А) 7 Б) 8 В) 9 Г) 10 Д) 11

11. Диана старше Ани, но моложе Кати. Боян старше Ани, а Виктор моложе Евы. Диана старше Бояна, а Катя моложе Виктора.

Кто старший из шестерых?

А) Диана Б) Боян В) Виктор Г) Катя Д) Ева

12. Семья состоит из отца, матери и ребенка. Сумма возрастов членов семьи — 49. За 3 года до этого она была 41. Сколько лет матери, если она на 21 год старше ребенка?

А) 23 Б) 24 В) 25 Г) 26 Д) 27

13. На пляже восемь детей. Известно, что какие бы трое из них ни вошли в воду, среди них будет по меньшей мере один, который умеет плавать. Какое наименьшее число детей, умеющих плавать, на пляже?

А) 3 Б) 4 В) 5 Г) 6 Д) 7

14. Сколькими различными способами можно разрезать фигуру на три пря-

моугольника?

А) 2 Б) 3 В) 4 Г) 5 Д) 6

15. В спортивном зале имеется шесть шкафов и в каждом шкафу — не менее трех мячей. Нет трех шкафов с одним и тем же

числом мячей. Какое наименьшее число мячей имеется в зале?

А) 21 Б) 24 В) 27 Г) 30 Д) 33

Ответы и краткие решения для 2 класса

1.Ответ В. 20 − 1 − 3 = 19 − 3 = 16.

2.Ответ Б. Проверьте самостоятельно.

3.Ответ В. B = 12 − 5 = 7, A = 12 − 3 = 9.

4.Ответ Б. С понедельника по пятницу на прошлой неделе

Фета похудела на четыре килограмма, а между двумя пятницами

еще на 7.

5.Ответ В. Среди этих чисел цифра 1 записана 2 раза в числе единиц, и 10 раз в числе десятков.

6.Ответ В. 22 + 22 + 22 + 22 = 88.

7.Ответ В. Среди этих чисел 9 начинаются с цифры 1, а еще 7 заканчиваются на 1; всего 16 чисел.

8.Ответ Д. Это четвертый вагон с головы состава, так что у нее сзади 6 вагонов.

9.Ответ В. Имеются 3 маленьких квадрата, 2 средних и один большой квадрат.

10. Ответ Б. Если отдадим 11-ти ребятам по одному яблоку (меньше мы не можем), то последнему останется 19−11 = 8 яблок. 11. Ответ Д. По условие К>Д>А, Б>А, E>В, Д>Б, В>К.

Следовательно, порядок от старшего к младшему Ева, Виктор, Ка-

тя, Диана, Боян, Аня.

12. Ответ А. Если ребенку не менее трех лет, то три года назад сумма возрастов членов семьи должна быть на 9 меньше, чем

49. Сейчас возраст ребенка 49 − 41 − 3 − 3 = 2, а тогда матери 21 + 2 = 23.

13. Ответ Г. Если только двое не умеют плавать, то условие выполняется. Если они соберутся вместе в море с кем-либо третьим, то он должен уметь плавать по условию задачи. Значит, остальные

шесть должны уметь плавать.

14. Ответ Г.

15. Ответ Б. 3 + 3 + 4 + 4 + 5 + 5 = 24.

Ответы 2 класс

1	2	3	4	5
В	Б	В	Б	В
6	7	8	9	10
В	В	Д	В	Б
11	12	13	14	15
Д	А	Г	Г	Б

Инструкция для 3–4 класса

1. Время работы 90 минут. Не разрешается использование калькуляторов и другой вычислительной техники.

можете соответствующее поле не заполнять, т.е. оставить поле за номером задачи пустым.

Замечание. Рисунки не обязательно точны — они только отоб-

ражают описываемую в условии конфигурацию.

Начисление очков:

• правильный ответ к каждой задаче — 7 очков;

• неуказанный ответ к задаче — 3 очка;

• неверный ответ — 0 очков.

Задачи для 3–4 класса

1. 201 − 3 + 20 − 13 =

А) 205 Б) 310 В) 180 Г) 210 Д) ни одно из перечисленных

2. Чему равны числа A и B на схеме A −⁺³→ B −·→²12 ?

А) A = 2, B = 6 Б) A = 9, B = 6

В) A = 6, B = 2 Г) A = 5, B = 9

Д) A = 3, B = 6

3. Знак какого действия нужно поставить на месте ∗ в равенстве

(20 ∗ 13) · 2 = 51, чтобы оно выполнялось?

А) сложение Б) вычитание В) деление Г) умножение

Д) ни одно действие не подходит

4.Каждый лестничный пролет между соседними этажами жилого дома имеет 23 ступени. На сколько ступеней нужно Ачо подняться с третьего этажа, чтобы оказаться у своего друга Чочо на одиннадцатом этаже?

А) 99 Б) 104 В) 154 Г) 117 Д) 138

5.Сколько всего квадратов на рисун-

ке?

А) 7 Б) 8 В) 9 Г) 10 Д) 11

6.Если в понедельник плавать две дистанции бассейна, во вторник — три, в среду — четыре и так же увеличивать их число каждый день, сколько всего дистанций окажется к субботе, включая ее?

А) 26 Б) 27 В) 28 Г) 29 Д) 30

7.Сумма возрастов у девочек Яны и Ани — 25. Яна на три года старше Ани. Сколько лет Ане?

А) 22 Б) 18 В) 14 Г) 12 Д) 11

8.Хамелеон начал двигаться от начала ветки длиной 1м, делая два шага вперед и один назад, каждый шаг за 2 секунды. Если длина шага 5см, то через сколько секунд хамелеон дойдет до конца ветки?

А) 58 Б) 116 В) 114 Г) 118 Д) ни одно из перечисленных

9.Сколькими разными способами можно разрезать фигуру на три прямо-

угольника?

А) 2 Б) 3 В) 4 Г) 5 Д) 6

10. Сок стоит 56ст., что на 24ст. дороже вафли. Сколько стотинок нужно, чтобы купить и сок, и вафлю?

А) 78 Б) 83 В) 88 Г) 93 Д) 98

11. Одна из 23 одинаковых на вид монет является более тяжелой чем остальные. Каким наименьшим числом взвешиваний весами можно определить отличающуюся монету?

А) 2 Б) 3 В) 4 Г) 5 Д) 6

12. На 4-х ветках дерева уселось 13 воробьев. Что можно утверждать с уверенностью?

А) на каждой ветке сидит не менее 3 воробьев

Б) на некоторой ветке сидит не менее 4 воробьев

В) нет ветки, на которой 5 воробьев

Г) на некоторой ветке сидит только один воробей

Д) на одной ветке 4 воробья, а на остальных по 3

13. Если раздать 20 яблок 13-и ребятам, так чтобы каждый получил не меньше одного яблока, то какое наибольшее число яблок может получить один из этих детей?

А) 7 Б) 8 В) 9 Г) 10 Д) 11

14. В ресторанe за квадратный стол можно посадить 4 человека. На рисунке показано как разместить 6 человек за двумя соединенными столами. Какое наименьшее число таких столов нужно соединить последовательно, чтобы разместить 12 человек?

• •

••

• •

А) 3 Б) 4 В) 5 Г) 6 Д) ни одно из перечисленных

15. Натуральные числа с 1 по 2013 записаны одно за другим:

1234567891011...20122013. Сколько раз записана цифра 2?

А) 212 Б) 414 В) 515 Г) 616 Д) ни одно из перечисленных

16. Семья состоит из отца, матери и ребенка. Сумма возрастов членов семьи — 49. За 3 года до этого она была 41. Сколько лет отцу, если мать на 21 год старше ребенка?

А) 23 Б) 24 В) 25 Г) 26 Д) 27

17. Дома вдоль одной улицы были занумерованы обычным образом: четные номера по одну сторону, нечетные по другую. При этом 2 стоит напротив 1, 4 напротив 3 и т.д. Начо прошелся по улице, начиная с №1. В конце прогулки он насчитал 10 цифр «2» на табличках с номерами на «нечетной» стороне улицы. До какого номера дома можно уверенно сказать, что дошел Начо?

А) №27 Б) №101 В) №129 Г) №205 Д) №227

18. Шесть котят и три мышонка весят столько же, сколько пять котят и 12 мышат. Весу скольких мышат равен вес двух котят?

А) 12 Б) 14 В) 16 Г) 18 Д) 20

19. Играя в казино в Лас-Вегасе, Джо всегда удваивает сумму денег, с которой начал игру. Но охранник берет у него 20 долларов за вход. Сколько долларов было у Джо перед первым вхождением в казино, если после третьего вхождения он обнаружил, что у него не осталось денег?

А) 20 Б) 40 В) 60 Г) 80 Д) ни одно из перечисленных

20. Поврежденный автомат для кофе выполняет следующие

действия:

1) за монету достоинства 1лв. выдает чашку кофе и две монеты

по 20ст.

2) за монету 20ст. — чашку кофе и монету 50ст.

3) за монету 50ст. — чашку кофе и монету 1лв.

Если у г-на Иванова была только одна монета достоинства 1лв. и он пользовался автоматом 4 раза, то какое наименьшее количество денег могло бы у него остаться после этого?

А) 1 лв. Б) 1 лв. 20 ст. В) 1 лв. 40 ст.

Г) 1 лв. 50 ст. Д) ни одно из перечисленных

Ответы и краткие решения для 3–4 класса

1.Ответ А. 201−3+20−13 = 188+20−13 = 218−13 = 205.

2.Ответ Д. B = 12 : 2 = 6, A = B − 3 = 6 − 3 = 3.

3.Ответ Д. Последовательно проверьте все действия и обнаружьте, что никакое из них не подходит. Еще один способ увидеть

это, что число, умноженное на два четно, а 51 нечетное.

4.Ответ Д. 23 + 23 + 23 + 23 + 23 + 23 = 138.

5.Ответ Д. Имеется 7 маленьких квадратов, три средних и один большой квадрат.

6.Ответ Б. 2 + 3 + 4 + 5 + 6 + 7 = 27.

7.Ответ Д. Если из возраста Яны вычесть три года, то получится удвоенный возраст Ани. Таким образом, возраст Ани равен (25 − 3) : 2 = 11.

8.Ответ Д. Первые 18 циклов “два шага вперед, один назад” займут у хамелеона по 6 секунд – всего 108 секунд. Хамелеон окажется в 10см от конца ветки. Ему остается сделать 2 шага вперед,

т.е. еще 4 секунды. Всего потребуется 112 секунд.

9.Ответ Г.

10. Ответ В. Вафля стоит 56−24 = 32 стотинки. Потребуется 32 + 56 = 88 стотинки.

11. Ответ Б. В первом взвешивании монеты разделены на три группы: (8,8,7), на весы положим две “восьмерки”. Если чаши весов в равновесии, то вторым взвешиванием “семерку” разделим на (3,2,2), а на весы поставим две “двойки”;

– если весы в равновесии, то третьим взвешиванием сравним двемонеты от “тройки” и определим тяжелую монету (которая может и

не быть на весах);

– если весы не в равновесии, то третьим взвешиванием сравнимпо одной монете от «тяжелой» “двойки”.

Аналогично рассматривается случай, когда одна из “восьмерок” тя-

желее.

Количество монет в “подозрительной” группе не может уменьшиться более чем в три раза за одно взвешивание, поэтому описан-

ная стратегия дает минимальное количество взвешиваний.

12. Ответ Б. Если на каждой ветке не более трех воробьев, то их общее количество не более 12. Пример, при котором оставшиеся

утверждения не верны: (5;3;3;2).

13. Ответ Б. Если отдать 12-ти ребятам по одному яблоку (меньше мы не можем), то последнему останется 20−12 = 8 яблок.

14. Ответ В. Каждый присоединенный стол дает 2 дополнительных места. Тогда за два стола могут сесть 6 человек, за 3 – 8, ...,

за 5 – 12 человек.

15. Ответ Г. В третьей и тринадцатой сотне цифра 2 встречается 120 раз, а в остальных 18 сотнях — по 20 раз. От 2000 до 2013 имеется 16 цифр 2. Следовательно, общее число двоек 240+18·20+ 16 = 616.

Второе решение: как число тысяч: 14 раз; как число сотен: 200;

как число десятков: 200; как число единиц: 202. Всего 616.

16. Ответ Б. Если ребенку не менее трех лет, то три года назад сумма возрастов членов семьи должна быть на 9 меньше, чем 49. Сейчас возраст ребенка 49 − 41 − 3 − 3 = 2, а тогда матери 21 + 2 = 23. Следовательно, отцу 49 − 23 − 2 = 24.

17. Ответ В. Цифра 2 на “нечетной” стороне сначала появляется на номерах 21, 23, 25, 27, 29 (имеем 5 цифр 2), а затем на

номерах 121, 123, 125, 127 и 129 (еще 5 цифр 2).

18. Ответ Г. Если вычесть по пять котят и три мышонка, получим, что один котенок весит столько же, сколько 9 мышат. Тогда

два котенка по весу равны 18 мышатам.

19. Ответ Д. Ответ: 35. Действительно, при третьем посещении казино Джо отдал охраннику 20 долларов. Это значит, что вторую партию он начал с 10 долларов. Перед этим у него было 10 + 20 = 30 долларов, что является удвоенной суммой, с которой он начал первую партию в казино, т.е. первая партия началась с 15 долларов. Следовательно, перед первым вхождением Джо имел 15 + 20 = 35 доллара.

20. Ответ Д. Сначала г-н Иванов опускает 1 лв. и получает

2 × 20 ст. После второго использования автомата у него останется 20 ст., а получил он еще 50 ст. При третьем броске монет:

i) может опустить 20 ст. и тогда получит 50 ст. Следовательно,при четвертом броске он может использовать только 50 ст. и при

этом получит 1 лв. и 50 ст.

ii) может опустить 50 ст. и получить 1 лв.; при четвертом броске:

– если опустит 20 ст., тогда останутся 1 лв. и 50 ст.

– если опустит 1 лв., тогда останутся 60 ст.

Ответы 3–4 класс

1	2	3	4	5	6	7	8	9	10
А	Д	Д	Д	Д	Б	Д	Д	Г	В
11	12	13	14	15	16	17	18	19	20
Б	Б	Б	В	Г	Б	В	Г	Д	Д

Инструкция для 5–6 класса

1. Время работы 90 минут. Не разрешается использование калькуляторов и другой вычислительной техники.

можете соответствующее поле не заполнять, т.е. оставить поле за номером задачи пустым.

Замечание. Рисунки не обязательно точны — они только отоб-

ражают описываемую в условии конфигурацию.

Начисление очков:

• правильный ответ к каждой задаче — 7 очков;

• неуказанный ответ к задаче — 3 очка;

• неверный ответ — 0 очков.

Задачи для 5–6 класса

1.20 · 13 − (20 − 13) =

А) 0 Б) 253 В) 167 Г) 541 Д) 308

2.Я купил печенье за 1,45лв. и сок за 1,82лв. Дав 10лв., сколько левов сдачи я должен ожидать?

А) 7,73 Б) 6,73 В) 6,83 Г) 7,83 Д) ни одно из перечисленных

3.Поезда метро ходят с интервалом в 6 минут с 8:00 до 9:00 и с интервалом в 7 минут с 9:00 до 10:00. Ачо сошел с поезда в 8:42 и пришел на ту же станцию метро в 9:30. Сколько минут он будет ждать поезда? (Простой поезда на станции не берется в расчет.)

А) 2 Б) 3 В) 4 Г) 5 Д) 6

4.В ребусе ОСА+ОСА=ЗЛО разным буквам отвечают разные цифры. Какое наибольшее значение может принимать сумма

А+О?

А) 10 Б) 9 В) 8 Г) 7 Д) ни одно из перечисленных

5.Если каждый из квадрати-

ков сетки — имеет длину стороны

C......

			......................................
			.......................................	...
...........				.........................................
..........................	......................................	......................................	......................................	.................................... ..................................

1см, то чему равна площадь _△ABC в квадратных сантиметрах?

A..

А) 10 Б) 10,5 В) 9 Г) 9,5^.....^B^.

Д) ни одно из перечисленных

6.Сколько имеется трехзначных квадратных чисел? (Квадратное число — это количество точек в квадрате — в каждой строке и в каждом столбце имеется одинаковое количество точек.)

А) 20 Б) 21 В) 22 Г) 23 Д) ни одно из перечисленных

7.В ресторанe за квадратный стол можно посадить 4 человека. На ри-

сунке показано как разместить 6 человек за двумя соединенными столами. Какое наименьшее число таких сто-

•

лов нужно соединить последователь-

но, чтобы разместить 20 человек?

А) 5 Б) 6 В) 10 Г) 12 Д) ни одно из перечисленных

8.Знаком Ψ перед натуральным числом обозначим число, записанное теми же цифрами что и данное число, но в обратном порядке; знак Θ перед числом обозначает сумму его цифр. Скобки и знак + имеют обычный смысл. Например: Ψ12 = 21, Θ412 = 4 + 1 + 2 = 7,

Ψ(1+Θ735) = Ψ(1+15) = 61. Чему равно Θ(Ψ(Θ4579)+Θ(Θ9438))?

А) 13 Б) 4 В) 14 Г) 49 Д) 67

9.Натуральные числа с 1 по 2013 записаны одно за другим:

1234567891011...20122013. Сколько раз записана цифра 2?

А) 212 Б) 414 В) 515 Г) 616 Д) ни одно из перечисленных

10. Хамелеон начал двигаться у начала ветки длиной 1м, делая два шага вперед и один назад, каждый шаг за 2 секунды. Если длина шага 5см, то через сколько секунд хамелеон дойдет до конца ветки? А) 118 Б) 116 В) 114 Г) 112 Д) ни одно из перечисленных

11. На 4-х ветках дерева уселось 13 воробьев. Что можно утверждать с уверенностью?

А) на каждой ветке сидит не менее 3 воробьев

Б) на некоторой ветке сидит не менее 4 воробьев

В) нет ветки, на которой 5 воробьев

Г) на некоторой ветке сидит только один воробей

Д) на одной ветке 4 воробья, а на остальных по 3

12. Поврежденный автомат для кофе выполняет следующие

действия:

1) за монету достоинства 1лв. выдает чашку кофе и две монеты

по 20ст.

2) за монету 20ст. — чашку кофе и монету 50ст.

3) за монету 50ст. — чашку кофе и монету 1лв.

А) 1лв. Б) 1лв. 20ст. В) 1лв. 40ст.

Г) 1лв. 50ст. Д) ни одно из перечисленных

13. Одна из 2013 одинаковых на вид монет является более тяжелой, чем остальные. Каким наименьшим числом взвешиваний на весах можно определить отличающуюся монету?

А) 6 Б) 7 В) 8 Г) 9 Д) 10

14. Точки C и D лежат на отрезке AB. Известно, что C в два раза ближе к A чем к B и D в три раза ближе к B чем к A. Если

длина CD 10см, то сколько сантиметров длина отрезка AB?

А) 24 Б) 30 В) 36 Г) 48 Д) 60

15. Прилавок для мороженого располагает большим количеством мороженого 6 видов. Сколькими разными способами можно заказать порцию мороженого, если в ней два шарика мороженого одного или разных видов?

А) 6 Б) 12 В) 15 Г) 18 Д) ни одно из перечисленных

16. В супермаркете пакуют поступившие яблоки в пакеты. В каждом должно быть одно и тоже количество яблок. Наполнили 52 пакета, осталось 8 яблок. Если бы в пакеты клали на два яблока меньше, то наполнилось бы без остатка 60 пакетов. Сколько было

яблок?

А) 480 Б) 540 В) 600 Г) 720 Д) 840

17. Дома вдоль одной улицы были занумерованы обычным образом: четные номера по одну сторону, нечетные по другую. При этом 2 стоит напротив 1, 4 напротив 3 и т.д. Чочо и Начо прошлись по улице, начиная с №1. В конце прогулки Начо насчитал 10 цифр «2» на табличках с номерами на «нечетной» стороне улицы. Какое наибольшее количество цифр «1» мог насчитать Чочо на табличках с «четной» стороны?

А) 20 Б) 40 В) 60 Г) 80 Д) ни одно из перечисленных

18. С самого начала 2013 года Живко кладет в копилку по понедельникам 5лв., а по четвергам 3лв. Сколько левов будет в копилке Живко к 1 ноября 2013г.? (1 января 2013г. было вторник.)

А) 344 Б) 345 В) 346 Г) 347 Д) ни одно из перечисленных

19. В следующих равенствах, написанных на языке

Сольресоль, слова обозначают цифры: редодо + ремими + ремими = релала редодо = ремими − редодо

Какая цифра соответствует релала?

А) 5 Б) 6 В) 7 Г) 8 Д) 9

20. Играя в казино в Лас-Вегасе, Джо всегда удваивает сумму денег, с которой начал игру. Но охранник берет у него 20 долларов за вход. Какая наименьшая сумма денег должна быть у Джо вначале, чтобы он мог входить в казино неограниченное число раз?

А) 20 Б) 40 В) 60 Г) 80 Д) ни одно из перечисленных

Ответы и краткие решения для 5–6 класса

1.Ответ Б. 20 · 13 − (20 − 13) = 260 − 7.

2.Ответ Б. 10 − 1,45 − 1,82 = 6,73.

3.Ответ Г. До 9:00 прошло три поезда, еще 4 до 9:28. В 9:35 следующий поезд.

4.Ответ Д. О не более 4 и четно, так как это число единиц числа 2А. Если О равно 4, то А может равняться 7, а тогда сумма 11 (417 + 417 = 834). Если О равно 2, то А может равняться 6. В

этом случае сумма меньше.

5.Ответ В. Сумма площадей трех треугольников, дополняющих данный треугольник до прямоугольника, равна

(3 · 3 + 5 · 1 + 4 · 2) : 2 = 11,

поэтому искомая площадь равна 20 − 11 = 9 кв. см.

6.Ответ В. Это числа 10², 11², ...30², 31².

7.Ответ Д. Каждый присоединенный стол дает 2 дополнительных места. Тогда возле n столов могут сидеть 2n + 2 человек.

Значит, 2n + 2 = 20, а n = 9.

8.Ответ А. Ψ(Θ4579) = 52, Θ(Θ9438) = 6, Θ(52 + 6) = 13.

9.Ответ Г. В третьей и тринадцатой сотне цифра 2 встречается 120 раз, а в остальных 18 сотнях - по 20 раз. От 2000 до 2013 имеется 16 цифр 2. Следовательно, общее число двоек 240+18·20+16 = = 616.

Второе решение: как число тысяч: 14 раз; как число сотен: 200; как число десятков: 200; как число единиц: 202. Всего 616.

10. Ответ Г. Первые 18 циклов “два шага вперед, один назад” займут у хамелеона по 6 секунд – всего 108 секунд. Хамелеон окажется в 10см от конца ветки. Ему остается сделать 2 шага вперед,

т.е. еще 4 секунды. Всего потребуется 112 секунд.

11. Ответ Б. Если на каждой ветке не более трех воробьев, то их общее количество не более 12. Пример, при котором оставшиеся

утверждения не верны: (5;3;3;2).

12. Ответ Д. Сначала г-н Иванов опускает 1 лв. и получает

этом получит 1 лв. и 50 ст.

ii) может опустить 50 ст. и получить 1 лв.; при четвертом броске:

– если опустит 20 ст., тогда останутся 1 лв. и 50 ст.

– если опустит 1 лв., тогда останутся 60 ст.

13. Ответ Б. Перед каждым взвешивании монеты делятся на

три группы: (671,671,671), (223,223,225), (75,75,73 или 75) и т.д. Достаточно взвесить две группы с равным количеством монет, чтобы

определить в какой из трех групп более тяжелая монета.

ная стратегия дает минимальное количество взвешиваний.

14. Ответ А. Пусть AB = 12x. Тогда AC = 4x, BD = 3x,

CD = AB − AC − BD = 5x. Значит, 5x = 10 см, следовательно, x =2 см, а тогда AB = 12 · 2 = 24 см.

15. Ответ Д. Имеется 6 порций мороженного с шариками одного вида и 6 · 5 : 2 = 15 порций с шариками различного вида; всего 6 + 15 = 21 порция.

16. Ответ Д. Имеем 52x + 8 = 60(x − 2) =⇒ 8x = 128 =⇒

x = 16. Искомое количество яблок 60 · 14 = 840.

17. Ответ В. До №129 включительно Начо насчитал 10 цифр

2. После №129 цифра 2 впервые появляется в доме с номером №201, но до него Чочо и Начо не дошли, иначе Начо бы насчитал 11 цифр 2. Следовательно, самый дальний дом с нечетным номером, до которого они могли дойти, это №199. Тогда Чочо мог считать число единиц в четных числах от 2 до 200. Такие единицы содержатся в номерах 10, 12, 14, 16, 18 (имеем 5 единиц); следующая группа четных чисел от 100 до 198 имеет по одной единице в разряде сотен (добавляется 50 единиц), и кроме того единицы в разряде десятков в числах 110, 112, 114, 116, 118 (еще 5 единиц). Таким образом, Чочо

мог насчитать самое большее 5+50+5=60 единиц.

18. Ответ Г. 2013 г. не является високосным, значит его продолжительность 365 дней. Следовательно от 1 января до 31 октября включительно прошло 365 - 31 - 30 = 304 дня. 7 января был понедельник, поэтому Живко положил в копилку 5 лв. Затем он опускал в капилку 5 лв. каждый понедельник. Так как (304 − 6) : 7 = 298 :

7 = 42 (остаток 4), то Живко опускал по понедельникам в копилку 5 лв. 43 раза, всего 43 · 5 = 215 лв. 3 января был четверг и тогда Живко опустил в копилку 3 лв. Затем он продолжал опускать в капилку 3 лв. каждый четверг. Так как (304 − 2) : 7 = 302 : 7 = 43

(остаток 1), Живко еще опускал по четвергам 3 лв. 44 раза, всего 3 · 44 = 132 лв. Итого к 1 ноября в копилке стало 215 + 132 = 347 лв.

19. Ответ А. Поскольку ремими цифра и равна двум редодо, то она может равняться 2, 4, 6 или 8. Но если ремими не менее 4, то редодо не менее 2, а релала не менее 10, что невозможно. Остается

случай, когда ремими равно 2, редодо равно 1, а релала – 5.

20. Ответ Б. Пусть X такая сумма денег, которая не меняется после уменьшения на 20 и последующего удвоения. Находим, что X = 40. Действительно, если Джо приходит к казино с 40 долларами, на входе отдает 20, а оставшиеся 20 долларов удваивает в казино. Таким образом, имея 40 долларов, Джо может посещать казино неограничено. Предположим теперь, что первоначально Джо идет в казино с суммой денег Y < 40. Обозначим A = 40−Y . После первого посещения казино у Джо останется сумма Y −A, т.е. сумма денег меньшая, чем та, с которой он вошел. Значит, разность между суммой на входе и суммой на выходе не менее A. Следовательно, через некоторое время, у Джо будет меньше чем 20 долларов, и он не сможет посетить казино. Это доказывает, что наименьшая сумма 40 долларов.

Ответы 5–6 класс

1	2	3	4	5	6	7	8	9	10
Б	В	Г	Д	В	В	Д	А	Г	Г
11	12	13	14	15	16	17	18	19	20
Б	Д	Б	А	Д	Д	В	Г	А	Б

Инструкция для 7–8 класса

1. Время работы 90 минут. Не разрешается использование калькуляторов и другой вычислительной техники.

можете соответствующее поле не заполнять, т.е. оставить поле за номером задачи пустым.

Замечание. Рисунки не обязательно точны — они только отоб-

ражают описываемую в условии конфигурацию.

Начисление очков: • правильный ответ к каждой задаче c номером от 1 до 8 включительно — 5 очков; • правильный ответ к каждой задаче c номером от 9 до 17 включительно — 7 очков; • правильный ответ к каждой задаче c номером от 18 до 25 включительно — 9 очков;

• неуказанный ответ к задаче — 3 очка;

• неверный ответ — 0 очков.

Задачи для 7–8 классa

1.201 · 3 − 20 · 13 =

А) 515 Б) 121 В) 343 Г) 252 Д) 474

2.Каждый день Ели кладет в копилку столько рублей, сколько дней в месяце. Сколько у нее накопилось за первые три месяца 2013го года?

А) 2645 р. Б) 2706 р. В) 2704 р.

Г) 2763 р. Д) 2804 р.

3.Сколько имеется трехзначных квадратных чисел? (Квадратное число — это количество точек в квадрате — в каждой строке и в каждом столбце имеется одинаковое количество точек.)

А) 20 Б) 21 В) 22 Г) 23 Д) ни одно из перечисленных

4.Одна из 2013 одинаковых на вид монет является более тяжелой, чем остальные. Каким наименьшим числом взвешиваний весами можно определить отличающуюся монету?

А) 6 Б) 7 В) 8 Г) 9 Д) 10

5.Группа экскурсантов ехала поездом. Ученики ехали со скидкой 75%, пенсионеры — 50%, а пассажиров с билетами по полной цене было в два раза больше, чем учеников, и в четыре раза больше, чем пенсионеров. Общая сумма поездки оказалась равной 30 полным билетам. Сколько было экскурсантов?

А) 30 Б) 36 В) 40 Г) 42 Д) ни одно из перечисленных

6.Чему равна сумма простых чисел p и q, для которых p+324 =

= q²?

А) 19 Б) 37 В) 46 Г) 56 Д) ни одно из перечисленных

7.Знаком Ψ перед натуральным числом обозначим число, записанное теми же цифрами, что и данное число, но в обратном порядке; знак Θ перед числом обозначает сумму его цифр. Скобки и знак + имеют обычный смысл. Например: Ψ12 = 21, Θ412 = 4+1+2 = 7,

Ψ(1+Θ735) = Ψ(1+15) = 61. Чему равно Θ(Ψ(Θ4579)+Θ(Θ9438))?

А) 13 Б) 4 В) 14 Г) 49 Д) 67

8.Половина участников марафона выбыла на пятом километре,

— на десятом, 10% — на двадцатом, 5% — на тридцатом, а до

финиша дошли 62 человека. Сколько всего было участников?

А) 2480 Б) 3620 В) 3720 Г) 7440 Д) 10 000

9.Из десятичных цифр x > y > z > 0 образованы всевоз-

можные трехзначные числа с различными цифрами. Сумма этих чисел — s. Сколько имеется множеств {x, y, z}, для которых s < 2013? А) 4 Б) 5 В) 6 Г) 7 Д) ни одно из перечисленных

10. Назовем диагональ выпуклого n-угольника большой, если она не разрезает данный многоугольник на треугольник и многоугольник. Сколько больших диагоналей у правильного 205-

угольника?

А) 10000 Б) 20130 В) 20500 Г) 25000

Д) ни одно из перечисленных

11. Для натуральных чисел n пусть P(n) — произведение десятичных цифр n (для однозначных n положим P(n) = n). Сколько имеется чисел m < 25, для которых P(P(m²)) = 0?

А) 2 Б) 4 В) 5 Г) 6 Д) 7

12. Боковые грани правильной четырехугольной пирамиды являются равносторонними треугольниками со сторонами 10м и облицованы мраморными плитами, которые также являются равносторонними треугольниками со сторонами 40см. Сколько плит использвано для облицовки?

А) 400 Б) 1000 В) 2500 Г) 4000

Д) ни одно из перечисленных

13. Точки C и D лежат на отрезке AB. Известно, что C в два раза ближе к A, чем к B и D в три раза ближе к B, чем к A. Если длина CD 15см, то какова длина AB в сантиметрах?

А) 24 Б) 30 В) 36 Г) 48 Д) 60

14. Сумма четвертых степеней трех простых чисел — 15282.

Чему равна сумма этих простых чисел?

А) 14 Б) 16 В) 17 Г) 18 Д) 20

15. На экскурсию каждый из пяти детей принес по шоколадке. Двое из них съели каждый свою собственную шоколадку, а каждый из остальных съел чужую шоколадку. Сколькими способами могло бы это случиться?

А) 10 Б) 20 В) 30 Г) 40 Д) 60

16. Если x+2y, y +2z, z +2x — простые числа, произведение которых равняется 2013, то чему равна сумма x + y + z?

А) 37 Б) 29 В) 25 Г) 19 Д) 16

17. В следующих равенствах, написанных на языке

Сольресоль, слова обозначают цифры: редодо + ремими + ремими = релала редодо = ремими − редодо

Какая цифра соответствует релала?

А) 9 Б) 8 В) 7 Г) 6 Д) 5

18. Точка I — внутренняя для треугольника со сторонами 3, 4 и 5см. Если I равноудалена от сторон, то на сколько миллиметров отстоит она от каждой?

А) 10 Б) 11 В) 12 Г) 13 Д) ни одно из перечисленных

19. Прилавок для мороженого располагает большим количеством мороженого 6 видов. Пиппи, Томми и Анника хотят купить себе каждый порцию по два шарика одного или разных видов мороженого, но так чтобы набор шариков у каждого отличался от остальных. Сколькими способами можно это сделать?

А) 7890 Б) 7980 В) 8790 Г) 8970 Д) 9780

20. На 100 карточках написали все натуральные числа от 1 до 100. Карточки перевернули. Какое наименьшее количество карточек надо взять наугад, чтобы быть уверенным, что среди чисел на выбранных карточках окажется не меньше двух взаимно простых?

А) 10 Б) 11 В) 50 Г) 90

Д) ни одно из перечисленных

21. В бесконечной десятичной дроби A = 13,3973... каждая цифра после запятой является цифрой единиц произведения двух предшествующих цифр. Какое из чисел равно A?

А) 13 Б) 13 В) 13 Г)

Д) ни одно из перечисленных

22. В командном соревновании по математике каждый ученик одной команды участвовал в решении двух задач, каждая задача решалась четырьмя учениками, а для любой пары задач только один ученик решал обе задачи. Сколько было учеников в команде?

А) 6 Б) 7 В) 8 Г) 9 Д) ни одно из перечисленных

23. Торт Каприча приготовлен из 5 крупных яиц (72ккал/шт.), 200г муки (2400ккал/кг), 150г сахара (3600ккал/кг) и 150г сливок (3000ккал/кг). Торт Буламача приготовлен из 3 небольших яиц (60ккал/шт.), 300г отрубей (1500ккал/кг), 180г заменителя сахара (500ккал/кг), 150г масла (7200ккал/кг). Г-жа Фета обычно ест 1/10 Каприча, но сегодня решила взять 1/10 Буламача. На сколько приблизительно килокалорий меньше примет г-жа Фета сегодня?

А) около 80 Б) около 40 В) около 20 Г) около 60

Д) разницы почти не будет

24. У какого из чисел

А) 2011 Б) 2012 В) 2013 Г) 2014

нет кратного в последовательности 4444, 44444, 444444, 4444444,...? Д) у каждого из указанных есть кратное

25. В слежке за жителями Фритауна, беспилотник вылетает из

точки А и выполняет 2013 раз следующее указание: лететь 1км вперед, повернуть 60^◦налeво,

после чего садится в точке В. Сколько километров расстояние меж-

ду точками А и В?

. •

А) 0 Б) 1 В) 2 Г) 3 Д) ни одно из перечисленных

Ответы и краткие решения для 7–8 класса

1. Ответ В.	201 · 3 − 20 · 13 = 603 − 260 = 343.
2. Ответ Б.	31 · 31 + 28 · 28 + 31 · 31 = 2706.

3. Ответ В. Это числа .

4. Ответ Б.

Перед каждым взвешивании монеты делятся на

определить в какой из трех групп более тяжелая монета.

5. Ответ Г. Пусть 4x пассажиров ехали с билетами по полной цене, тогда учеников было 2x, а пенсионеров – x. Обозначим цену од-

ного билета a и составим уравнение

, откуда получаем x = 6, т.е. общее число

экскурсантов – 42.

6. Ответ Г. p = (q − 18)(q + 18) =⇒ q = 19 =⇒ p = 37.

7. Ответ А. Ψ(Θ4579) = 52, Θ(Θ9438) = 6, Θ(52 + 6) = 13.

8. Ответ В.

= 62 · 60.

9. Ответ Г. Поскольку s = 222(x + y + z) < 2013, имеем x+y+z < 10. Если z > 2, то x+y+z ≥ 5+4+3 > 10. Следовательно z = 1 или z = 2. При z = 1 и y = 2, имеется 4 множества, в которых x ∈ {3, 4, 5, 6}, а если y = 3, то существуют два множества –

x ∈ {4, 5}. При z = 2 есть еще одно множество: {4, 3, 2}.

10. Ответ В. Число больших диагоналей вычисляется по форn(n − 5) муле .

11. Ответ Д. Равенство P(P(m²)) = 0 возможно в двух случаях: m²содержит: а) цифру 0; б) одна цифра 5, а другая четная. Числа m первого вида 10 и 20, а второго вида 5, 15, 16, 23 и 24.

12. Ответ В. Вдоль каждого ребра любой грани выложено

25 плиток: в первом ряду одна плитка, во втором 3, в третьем 5 и т.д. Потребуется 25²плиток для облицовки одной грани. Всего 4 · 25²= 100 · 25 = 2500.

13. Ответ В. Пусть AB = 12x. Тогда AC = 4x, BD = 3x,

CD = AB − AC − BD = 5x. Имеем 5x = 15 см, значит x = 3 см, а тогда AB = 12 · 3 = 36 см.

14. Ответ Г. Одно из чисел 2. Сумма четвертых степеней двух других чисел равна 15266. Четвертые степени могут заканчиваться на 0, 1, 5 или 6. Поскольку искомые числа нечетны, то одно из них 5. Тогда p⁴= 14641, а p = 11.

15. Ответ Б. Имеем способов выбрать двух детей,

которые ели собственные шоколадки. Остальные трое детей могут обменяться шоколадками 2-мя способами (если они встанут, образуя круг, то они смогут обменяться по часовой стрелке или против). Ответ: 10 · 2 = 20.

16. Ответ В. Поскольку 2013 = 3 · 11 · 61, имеем x + 2y + y +

+2z +z +2x = 3+11+61 = 75, откуда x+y +z = 25. x = 25, y = = −11, z = 11 единственное решение системы.

17. Ответ Д. Поскольку ремими цифра и равна двум редодо, то она может равняться 2, 4, 6 или 8. Но если ремими не менее 4, то редодо не менее 2, а релала не менее 10, что невозможно. Остается случай, когда ремими равно 2, редодо равно 1, а релала – 5.

18. Ответ А. Площадь треугольника равна 6 кв. см. (египетский треугольник). Пусть искомое расстояние r сантиметров, тогда

имеем .

19. Ответ Б. Имеем 6 различных порций мороженого с шариками одного вида и 6 · 5 : 2 = 15 порций с шариками разного вида. Требуется выбрать 3 порции из 6 + 15 = 21, что можно сделать 21 · 20 · 19 = 7980 способами.

20. Ответ Д. Ответ: 51. Перевернуть 50 или меньшее количество карточек недостаточно, так как от 1 до 100 находится 50 четных чисел, любая пара которых не является взаимно простыми. Если перевернуть 51 карточку, то среди полученных чисел будут по крайней мере два последовательных, которые дадут искомую пару взаимно простых. Действительно, если предположить, что последовательных чисел нет и n ≥ 1 наименьшее из полученных чисел, то наибольшее полученное число не меньше чем n + 2 · 50 > 100.

21. Ответ В. При последовательном вычислении цифр после запятой получим, что 6-я и 7-я цифры 3. Также две последовательные тройки находятся в начале числа (число единиц и десятых равно 3). Тогда цифра на 8 позиции после запятой совпадает с цифрой на второй позиции, а цифра на 9-й позиции совпадает с цифрой на 3-й

и т.д. Таким образом, находим, что период A равен (397313). Пусть 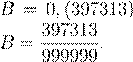. Тогда 1000000B − 397313 = B, откуда получим

22. Ответ Д. Моделью данной задачи является правильный пятиугольник с проведенными диагоналями: вершины – задачи, а диагонали – ученики. Так как число диагоналей равно 10, то и учеников тоже 10.

23. Ответ Д. Количество килокалорий в торте Каприча

5·72+2400·0,2+3600·0,15+3000·0,15 = 1830. Число килокалории в торте Буламача 3·60+1500·0,3+500·0,18+7200·0,15 = 1800. Фета экономит 183 − 180 = 3 килокалории.

24. Ответ Д. Любое число m, заканчивающееся на 1, 3, 7 или

9, имеет кратное число вида 11...11. Действительно, в последовательности 1111, 11111, 111111, 1111111,... найдутся числа с равными остатками при деление на m, следовательно разность этих чисел является числом вида 11...11 · 10ⁿ. Так как НОД(m;10ⁿ) = 1, то m делит 11...11. Поскольку 2012 = 4 · 503 и 2014 = 2 · 1007, то каждое из приведенных чисел имеет кратное в последовательности 4444, 44444, 444444, 4444444,....

25. Ответ В. Траектория беспилотника является правильным шестиугольником. Через каждые 6 указаний он пролетает над точкой А. Поскольку 2013 = 6 · n + 3, точка B диаметрально противоположна точке А в описанной окружности, радиус которой 1 км.

Ответы 7–8 класс

1	2	3	4	5	6	7	8	9	10
В	Б	В	Б	Г	Г	А	В	Г	В
11	12	13	14	15	16	17	18	19	20
Д	В	В	Г	Б	В	Д	А	Б	Д
21	22	23	24	25
В	Д	Д	Д	В

Инструкция для 9–10 класса

1. Время работы 90 минут. Не разрешается использование калькуляторов и другой вычислительной техники.

можете соответствующее поле не заполнять, т.е. оставить поле за номером задачи пустым.

Замечание. Рисунки не обязательно точны — они только отоб-

ражают описываемую в условии конфигурацию.

Начисление очков: • правильный ответ к каждой задаче c номером от 1 до 10 включительно — 5 очков; • правильный ответ к каждой задаче c номером от 11 до 20 включительно — 7 очков; • правильный ответ к каждой задаче c номером от 21 до 30 включительно — 9 очков;

• неуказанный ответ к задаче — 3 очка;

• неверный ответ — 0 очков.

Задачи для 9–10 классa

1.2013 − 2012 + 2011 − 2010 + ··· + 3 − 2 + 1 =

А) 1005 Б) 1006 В) 1007 Г) 1008 Д) ни одно из перечислен-

ных

2.Для какого значения параметра p уравнение

x²+ 2013x + p = 0 имеет корни с различными знаками?

А) −2013 Б) 2013 В) 2012 Г) 2014 Д) 0

3.Группа экскурсантов ехала поездом. Ученики ехали со скидкой 75%, пенсионеры — 50%, а пассажиров с билетами по полной цене было в два раза больше, чем учеников, и в четыре раза больше, чем пенсионеров. Общая сумма поездки оказалась равной 30 полным билетам. Сколько было экскурсантов?

А) 30 Б) 36 В) 40 Г) 42 Д) никое от тези

4.Если для каждого вещественного x определено

f(x − 1) = x²− 3x + 1, то:

А) f(x) = x²− x − 1 Б) f(x) = x²− 3x − 1

В) f(x) = x²+ x + 1 Г) f(x) = x²+ 3x + 1

Д) ни одно из перечисленных

5.Сколько имеется трехзначных треугольных чисел? (Треугольное число t_n— это количество точек в равностороннем треугольнике со стороной n; t₁= 1, t_n= t_n−1 + n.)

А) 29 Б) 30 В) 31 Г) 32

Д) ни одно из перечисленных

6.Какое наибольшее двузначное число невозможно представить суммой двух простых чисел?

А) 99 Б) 98 В) 97 Г) 96 Д) 95

7.Если t — количество трехзначных чисел, у которых все цифры являются различными простыми числами, а c — количество четырехзначных чисел, у которых все цифры различные простые числа, то чему равно t : c?

А) Б) В) Г) Д) 1

8.Стороны выпуклого четырехугольника ABCD находятся в

отношении AB : BC : CD : DA = 1 : 2 : 4 : 3. Вписанные в _△ABD и _△CBD окружности касаются BD в точках M и N. Чему равно отношение MN : BD?

А) Б) Г) Д) ни одно из перечисленных

9.Если x + 2y, y + 2z, z + 2x — простые числа, произведение которых равняется 2013, то чему равна сумма x + y + z?

А) 37 Б) 29 В) 25 Г) 19 Д) 16

10. Из десятичных цифр x > y > z > 0 образованы всевоз-

можные трехзначные числа с различными цифрами. Сумма этих чисел — s. Сколько имеется множеств {x, y, z}, для которых s < 2013? А) 7 Б) 6 В) 5 Г) 4 Д) ни одно из перечисленных

11. Боковые грани правильной четырехугольной пирамиды являются равносторонними треугольниками со сторонами 10м и облицованы мраморными плитами, которые также являются равносторонними треугольниками со сторонами 40см. Сколько плит использовано для облицовки?

А) 400 Б) 1000 В) 2500 Г) 4000

Д) ни одно из перечисленных

12. Для натуральных чисел n пусть P(n) — произведение десятичных цифр n (для однозначных n положим P(n) = n). Сколько имеется чисел m < 25, для которых P(P(m²)) = 0?

А) 2 Б) 4 В) 5 Г) 6 Д) 7

13. В командном соревновании по математике каждый ученик одной команды участвовал в решении двух задач, каждая задача решалась четырьмя учениками, а для любой пары задач только один ученик решал обе задачи. Сколько было учеников в команде?

А) 6 Б) 7 В) 8 Г) 9 Д) ни одно из перечисленных

14. Каждая из трех окружностей с радиусом 1 внешне касается двух других. Чему равен радиус окружности, внешне касающейся данных трех? А) − 1 Б)В) 2 − √3 Г) 2 − √3

√3

22 3

Д) ни одно из перечисленных

15. Точка P лежит на стороне

AB _△ABC, а M и N — центры C

..........................................................................

часть площадитяжести △APC△иABC△BPCсоставляет. Какую ......................^............................................. ............................._..............................

...... ..

площадь _△PNM?

1 1 3 5

А) Б) В) Г)

9 6 8 18

Д) ни одно из перечисленных

16. Чему равен остаток от деления 2013²⁰¹³на 13?

А) 5 Б) 8 В) 1 Г) 2 Д) 11

17. К трем из сторон правильно-

го шестиугольника внешне построе- .........................................Q.................. ...................................................................................... ......................................................................................P...........................................................

ны равносторонние треугольники с центрами N, P, Q, как показано на рисунке. Какую часть площади ше-

стиугольника составляет _△NPQ?

2 4 3 9

А) Б) В) Г) Д) ни одно из перечисленных

3 9 4 16

18. Чему равна площадь фигуры, образованной точками с координатами (x;y), для которых 1 ≤ |x| + |y| ≤ 2?

А) 1 Б) 3 В) 4 Г) 6 Д) 7

19. Назовем диагональ выпуклого n-угольника большой, если она не разрезает данный многоугольник на треугольник и многоугольник. Число всех больших диагоналей некоторого выпуклого n-угольника — 2013. Чему равно n?

А) 66 Б) 61 В) 65 Г) 67

Д) ни одно из перечисленных

20. Сколькими способами делегацию из 11 человек можно перевезти на четырех внешне неразличимых машинах, если в каждой из них можно разместить не более трех человек?

А) 9240 Б) 15400 В) 30800 Г) 46200

Д) ни одно из перечисленных

21. На 100 карточках написали все натуральные числа от 1 до 100. Карточки перевернули. Какое наименьшее количество карточек надо взять наугад, чтобы быть уверенным, что среди чисел на выбранных карточках окажется не меньше двух взаимно простых?

А) 10 Б) 11 В) 50 Г) 90 Д) ни одно из перечисленных

22. Последовательность a_n= b_nc_n, b_n,c_n∈ {0;1;2;3;4;5;6;7;8;9} определена равенствами a₁= 16, a_n₊₁= b_n+ c²_nдля ⁿ∈ N. Чему

равно a₂₀₁₃?

А) 9 Б) 16 В) 37 Г) 52 Д) 81

23. Сколько вещественных решений имеет система

А) 4 Б) 3 В) 2 Г) 1 Д) нет решений

24. На экскурсию каждый из десяти детей принес по шоколадке. Шестеро из них съели каждый свою собственную шоколадку, а каждый из остальных съели чужую шоколадку. Сколькими способами могло бы это случиться?

А) 210 Б) 420 В) 840 Г) 1890 Д) 5040

25. Сколько из чисел 1,2,3,...,2013 имеют кратные вида

444...44?

А) 1208 Б) 1410 В) 1511 Г) 1612

Д) ни одно из перечисленных

26. Торт Каприча приготовлен из 5 крупных яиц (72ккал/шт.), 200г муки (2400ккал/кг), 150г сахара (3600ккал/кг) и 150г сливок (3000ккал/кг). Торт Буламача приготовлен из 3 небольших яиц (60ккал/шт.), 300г отрубей (1500ккал/кг), 180г заменителя сахара (500ккал/кг), 150г масла (7200ккал/кг). Г-жа Фета обычно ест 1/10 Каприча, но сегодня решила взять 1/10 Буламача. На сколько приблизительно килокалорий меньше примет г-жа Фета сегодня?

А) около 80 Б) около 40 В) около 20 Г) около 60

Д) разницы почти не будет

27. В следующих равенствах, написанных на языке Сольресоль, слова обозначают цифры:

редодо + ремими + солдо + рефафа = ресиси ремими × рефафа = ресиси

Найдите сумму ремими + рефафа + ресиси.

А) 14 Б) 13 В) 12 Г) 11 Д) 10

28. Сколько имеется трехзначных чисел abc, для которых a · b · c = 2⁴3³?

А) 3 Б) 6 В) 8 Г) 9 Д) 12

29. Плитки некоторой большой крыши сначала сухие. На самую верхнюю из них начинает капать. Если

плитка сухая, то капля остается на месте. Если на плитке уже есть капля, она сливается с новой каплей и получившаяся б`ольшая капля соскальзыва-

ет на следующую плитку.

Там происходит то же самое: капля либо останавливается, либо — если на плитке уже есть капля — сливается с ней и полученная еще большая капля сползает вниз и т.д. На скольких из плиток будут капли, после того, как 2013-я капля остановится?

А) 8 Б) 9 В) 10 Г) 11

Д) ни одно из перечисленных

30. Сколько строк напечатает процедура башня(n: целое; s: буква, cherez: буква, na: буква) если n>0 то

{башня(n-1, s, na, cherez); напечатать(’сдвинуть диск с ’, s, ’ на ’, na); башня(n-1, cherez, s, na)} при вызове башня(10,А,Б,В)?

А) меньше 10 Б) от 10 до 100 В) от 101 до 1000

Г) от 1001 до 10000 Д) больше 10000

Ответы и краткие решения для 9–10 класса

1.Ответ В. Представьте в виде суммы такого количества единиц, сколько нечетных чисел от 1 до 2013.

2.Ответ А. По теореме Виета x₁x₂< 0 ⇐⇒ p < 0.

3.Ответ Г. Пусть 4x пассажиров ехали с билетами по полной цене, тогда учеников было 2x, а пенсионеров – x. Обозначим цену од-

ного билета a и составим уравнение

, откуда получаем x = 6, т.е. общее число

экскурсантов – 42.

4.Ответ А. Имеем f(x) = f((x + 1) − 1) = (x + 1)²− 3(x + + 1) + 1 = x²− x − 1.

5.Ответ В. Так как , то t_n– трехзначное, если

200 ≤ n²+ n < 2000. Трехзначные треугольные числа: t₁₄,..., t₄₄.

6. Ответ В. Четные числа не являются искомыми (98=79+19,

96=79+17). Если сумма двух простых чисел нечетна, то одно из них равно 2. Проверим, что 99 − 2 простое, а 97 − 2 = 95 составное. Значит, 97 не представимо в виде суммы двух простых чисел.

7. Ответ Д. Трехзначных и четырехзначных чисел с указанным свойством 4 · 3 · 2.

8. Ответ Д. Ответ: 0. В _△ABD находим

. Поскольку AB+CD =

= BC + DA, имеем BM = BN, т.е. M ≡ N.

9. Ответ В. Поскольку 2013 = 3 · 11 · 61, имеем x + 2y + y +

+2z +z +2x = 3+11+61 = 75, откуда x+y +z = 25. x = 25, y =

= −11, z = 11 единственное решение системы.

10. Ответ А. Поскольку s = 222(x + y + z) < 2013, имеем x+y+z < 10. Если z > 2, то x+y+z ≥ 5+4+3 > 10. Следовательно z = 1 или z = 2. При z = 1 и y = 2, имеется 4 множества, в которых x ∈ {3, 4, 5, 6}, а если y = 3, то существуют два множества –

x ∈ {4, 5}. При z = 2 есть еще одно множество: {4, 3, 2}.

11. Ответ В. Вдоль каждого ребра любой грани выложено

12. Ответ Д. Равенство P(P(m²)) = 0 возможно в двух случаях: m²содержит: а) цифру 0; б) одна цифра 5, а другая четная. Числа m первого вида 10 и 20, а второго вида 5, 15, 16, 23 и 24.

13. Ответ Д. Моделью данной задачи является правильный пятиугольник с проведенными диагоналями: вершины – задачи, а диагонали – ученики. Так как число диагоналей равно 10, то и уче-

ников тоже 10.

14. Ответ Б. Центры единичных окружностей образуют равносторонний треугольник со стороной 2 и, следовательно, с радиусом описанной окружности . От этого радиуса необходимо вы-

честь радиус данных окружностей.

15. Ответ А. Применяя теорему Фалеса, последовательно

найдем где точки M^′и N^′

середины AP и BP; кроме того h_P= h_C. Тогда S_PNM: S_ABC=

16. Ответ Б. Применим сравнения 2013 ≡ −2( mod 13), 2⁶≡

≡ −1( mod 13). Тогда получим 2013²⁰¹³≡ (−2)²⁰¹³≡ −(2⁶)³³⁵· 2³≡ ≡ 8( mod 13).

17. Ответ А. Проекции точек P и Q на стороны равносторонних треугольников делят их пополам, поэтому PQ вдвое больше стороны шестиугольника. Тогда _△NPQ состоит из четырех равносторонних треугольников, а шестиугольник – из шести таких же,

как и внешне построенные. Следовательно, искомое отношение 4:6.

18. Ответ Г. Фигура состоит из точек между двумя квад-

ратами , следовательно, её площадь

(2√2)²− √2 = 6.

n(n − 5)

19. Ответ А. Количество больших диагоналей . Сле-

довательно, n(n − 5) = 2 · 3 · 11 · 61 = 66 · 61.

20. Ответ Б. Условие будет выполнено, если в трех машинах

по три человека, а в четвертой два. Двух делегатов можно выбрать 11 · 10

= 55 способами. Оставшиеся 9 делегатов могут быть расса2

жены по машинам A, B, C способами. Поскольку

машины неразличимы, то необходимо разделить на 3! = 6, получим 2 · 7· 5· 4 = 7 · 40 способов. Окончательный ответ 55· 40· 7 = 15400.

21. Ответ Д. Ответ: 51. Перевернуть 50 или меньшее количество карточек недостаточно, так как от 1 до 100 находится 50 четных чисел, любая пара которых не является взаимно простыми. Если перевернуть 51 карточку, то среди полученных чисел будут по крайней мере два последовательных, которые дадут искомую пару взаимно простых. Действительно, если предположить, что последовательных чисел нет и n ≥ 1 наименьшее из полученных чисел, то наибольшее полученное число не меньше чем n + 2 · 50 > 100.

22. Ответ Д. Последовательность 16, 37, 52, a₄= 09, a₅= 81, a₆= 09, a₇= 81,... Поскольку 2013 нечетно, то на 2013 позиции

стоит 81.

23. Ответ Г. Так как y+z = 2√2 и yz = x²+2, то y и z корни

уравнения t²− 2√2t + x²+ 2 = 0, т.е. (t − √2)²+ x²= 0. Данное уравнение имеет решение только тогда, когда x = 0 и t_1,2= √2.

24. Ответ Г. , где !n число беспорядков

на n элементах; вычисляется по рекуррентному соотношению !n = = (n − 1)(!(n − 1)+!(n − 2)), !1 = 0, !2 = 1.

25. Ответ Б. Числа 4, 44 и 444 не делятся на 8. Тогда по признакам деления на 8 и на 5 числа вида 444...44 не делятся ни на 5, ни на 8. Все числа, которые не делятся на 5 или 8, представимы в виде произведения одного из чисел 1, 2 или 4, на число n, заканчивающееся на 1, 3, 7 или 9. По принципу Дирихле, любое число n заканчивающееся на 1, 3, 7 или 9 имеет кратное вида 111...11. Но тогда числа n, 2n и 4n имеют кратное вида 444...44. Таким образом, число 444...44 может быть кратно любому числу, которое не делится на 5 или 8. Имеем 2010 : 5 = 402 числа кратных 5, 2008 : 8 = 251 число кратное 8 и 2000 : 40 = 50 чисел кратных 5 и 8. Ответ: 2013 − 402 − 251 + 50 = 1410.

26. Ответ Д. Количество килокалорий в торте Каприча

27. Ответ Г. Так как ресиси цифра и произведение двух других, это 4, 6, 8 или 9. Только 6 можно представить в виде суммы четырех различных меньших чисел, два из которых являются его множителями: 6 = 0+1+2+3 = 2×3. Тогда ресиси равно 6, а ремими и рефафа это 2 и 3(и действительно в таком порядке; редодо – 1, солдо – 0).

28. Ответ Б. Пусть a ≤ b ≤ c. Тогда a > 4 (иначе bc = 2⁴3³: a трехзначно). При a = 6 имеем bc = 72, откуда b = 8, c = 9. Если a ≥ 8, то c = 9, но тогда b ≤ 6 – противоречие. Тогда единственная

возможная тройка цифр {6, 8, 9}.

29. Ответ Б. Если считать, что каждая падающая капля имеет массу 1, то капля, попавшая на n-ю плитку, будет иметь массу 2ⁿ⁻¹. Это означает, что плитка, на которой остановилась m-я капля соответствует наименьшей степени двойки (начиная с 2⁰), содержащейся в двоичном разложении m. Так как 2013 = 11111011101₂, то

капли будут на 9 плитках.

30. Ответ Г. Процедура описывает рекурсивное решение задачи о ханойских башнях (с минимальным числом перемещений). Это число T_nудовлетворяет рекуррентному соотношению: T₁= 1, T_n=

= 2T_n−1 + 1. При всех натуральных n получим, что T_n= 2ⁿ− 1.

Ответы 9–10 класс

1	2	3	4	5	6	7	8	9	10
В	А	Г	А	В	В	Д	Д	В	А
11	12	13	14	15	16	17	18	19	20
В	Д	Д	Б	А	Б	А	Г	А	Б
21	22	23	24	25	26	27	28	29	30
Д	Д	Г	Г	Б	Д	Г	Б	Б	Г

Инструкция для 11–12 класса

1. Время работы 90 минут. Не разрешается использование калькуляторов и другой вычислительной техники.

можете соответствующее поле не заполнять, т.е. оставить поле за номером задачи пустым.

Замечание. Рисунки не обязательно точны — они только отоб-

ражают описываемую в условии конфигурацию.

• неуказанный ответ к задаче — 3 очка;

• неверный ответ — 0 очков.

Задачи для 11–12 классa

1.lg2013²− 2lg2013 =

А) 0 Б) 1 В) 10 Г) 100 Д) 1000

2.Какое из чисел

А) 2013 Б) 2014 В) 2015 Г) 2016 Д) 2017

является членом арифметической прогрессии с первым членом 3 и

разностью 671?

3.Если для каждого вещественного x определено

f(x − 1) = x²− 3x + 1, то:

А) f(x) = x²− 3x − 1 Б) f(x) = x²− x − 1

В) f(x) = x²+ x + 1 Г) f(x) = x²+ 3x + 1

Д) ни одно из перечисленных

4.Сколько корней имеет уравнение sin²x + 2cosx − 2 = 0 на

отрезке [0;π]?

А) 0 Б) 1 В) 2 Г) 3 Д) 4

А) 29 Б) 31 В) 34 Г) 37 Д) ни одно из перечисленных

6.Каковы наименьшее и наибольшее значения функции f(x) =

= sin²x + 2cosx, x ∈ [0;π]?

А) fmin = −2, fmax = 2 Б) fmin = −1, fmax = 1

В) fmin = 0, fmax = 2 Г) fmin = −2, fmax = 1

Д) ни одно из перечисленных

7.Какое наибольшее двузначное число невозможно представить суммой двух простых чисел?

А) 99 Б) 98 В) 97 Г) 96 Д) 95

8.Случайным образом выбирается трехзначное число. Какова вероятность того, что все три цифры оказались различными простыми числами?

А) Б) В) Г) Д)

9.Стороны выпуклого четырехугольника ABCD находятся в

А) Б) В) Г) Д) ни одно из перечисленных

10. Точка P лежит на стороне AB _△ABC, а M и N — цен-

......................................C......................................................................^.........трыAPC и _△BPC. Какую часть ....................................

. .

... .

площади △ABC составляет пло- ......................^....................^............. ^{........................}_...........................

M ............ N .

щадь _△PNM?

А) Б) В) Г) Д) ни

одно из перечисленных

11. Чему равна площадь фигуры, образованной точками с координатами (x;y), для которых 1 ≤ |x| + |y| ≤ 2?

А) 1 Б) 3 В) 4 Г) 6 Д) 7

12. Чему равен коэффициент перед x⁻³после раскрытия скобок

и приведения подобных членов выражения ?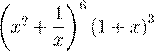

А) 1 Б) 3 В) 6 Г) 7 Д) ни одно из перечисленных

13. Для каких значений параметра m решениями неравенства

4(mx)²≤ 4x⁴+ 1 являются все числа x ∈ (−∞;+∞)?

А) m ∈ (−∞;0] Б) m ∈ (−2;2) В) m ∈ [0;+∞)

Г) m ∈ [−1;1] Д) ни одно из перечисленных

14. Чему равен остаток от деления 2013²⁰¹³на 13?

А) 5 Б) 8 В) 1 Г) 2 Д) 11

15. Две диагонали дельтоида равны 4, а две его стороны — √5. Чему равна каждая из остальных двух сторон?

А) √10 Б) √8 В) √14 Г) √12 Д) ни одно из перечисленных

16. Какое наименьшее число, записанное в системе счисления с основанием 4, имеет сумму цифр 2013₄?

А) 2⁹⁰− 1 Б) 3⁴⁵− 1 В) 4⁵⁰³− 1 Г) 2013⁴

Д) ни одно из перечисленных

17. К трем из сторон правильного шестиугольника внешне _..

построены равносторонние треугольники с центрами N, P, Q, как показано на рисунке. Какую часть площади шестиугольника

составляет _△NPQ?

4 3 2 9

А) Б) В) Г) Д) ни одно из перечисленных

9 4 3 16

18. Каждая из трех окружностей с радиусом 1 внешне касается двух других. Чему равен радиус окружности, внешне касающейся данных трех?

√3 − 12 − √3

А) Б)В)Г)

Д) ни одно из перечисленных

19. На абитуриентский бал идут 10 пар абитуриентов. После бала каждый парень провожал одну из девушек до ее дома. Какова вероятность того, что ровно пять из парней провожали каждый ту же самую девушку, с которой пришел на бал?

А) больше 0,5 Б) от 0,1 до 0,5

В) от 0,01 до 0,05 Г) от 0,001 до 0,005

Д) ниже 0,001

20. В прямоугольнике ABCD AB = 10 и BC = 5. Выбирая

различные положения точки X на стороне CD, определите каково наименьшее возможное значение выражения

y = 3AX²+ BX².

А) 120 Б) 175 В) 144 Г) 150

Д) ни одно из перечисленных

21. Сколько решений имеет система ?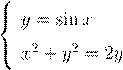

А) 0 Б) 1 В) 2 Г) 3 Д) ни одно из перечисленных

22. Сколько из чисел 1,2,3,...,2013 имеют кратные вида

888...88?

А) 1208 Б) 1410 В) 1511 Г) 1612

Д) ни одно из перечисленных

23. Сколько вещественных решений имеет система

А) 0 Б) 1 В) 2 Г) 4 Д) бесконечно много

24. В следующих равенствах, написанных на языке Сольресоль, слова обозначают цифры:

редодо + ремими + сольдо + рефафа = ресиси ремими × рефафа = ресиси

Найдите сумму ремими + рефафа + ресиси.

А) 10 Б) 11 В) 12 Г) 13 Д) 14

25. В правильном пятиугольнике ABCDE биссектрисса ∠BEA пересека-

ет AC в точке Q. Чему равно CQ : AQ?

√ 1 + √5 √

А) 2 + 5 Б) В) 1 + 5

Г) 5 Д) ни одно из перечисленных

26. Сколько имеется трехзначных чисел abc, для которых a·b· c = 2⁴3³?

А) 12 Б) 9 В) 8 Г) 6 Д) 3

27. Плитки некоторой большой крыши сначала сухие. На самую верхнюю из них начинает капать. Если

плитка сухая, то капля остается на месте. Если на плитке уже есть капля, она сливается с новой каплей и получившаяся б`ольшая капля соскальзывает на нижную плитку.

Там происходит то же самое: капля либо останавливается, либо —если на плитке уже есть капля —- сливается с ней и полученная еще большая капля сползает вниз и т.д. На скольких из плиток будут капли, после того, как 2013-я капля остановится?

А) 11 Б) 10 В) 9 Г) 8 Д) ни одно из перечисленных

28. Пятиугольное число P_n— количество точек, которые умещаются в фигуре, состоящей из квадрата n × n, над котором расположен треугольник с основанием стороны квадрата. На рисун-

ке это показано для n = 4. Чему равно

Б) В) 2 Г) Д) ни одно

из перечисленных

29. Сколько строк напечатает процедура

• • • •

башня(n: целое; s: буква, cherez: буква, na: буква) если n>0 то

{башня(n-1, s, na, cherez); напечатать(’сдвинуть диск с ’, s, ’ на ’, na); башня(n-1, cherez, s, na)} при вызове башня(10,А,Б,В)?

А) меньше 10 Б) от 10 до 100 В) от 101 до 1000

Г) от 1001 до 10000 Д) больше 10000

30. Боковые грани единичного куба в прямоугольной системе координат сделаны зеркальными. Луч света с началом в точке (0,5;0;0) отражается в точке (1;0,5;0,25). В какой точке окажется луч, встречая поверхность куба в четвертый раз? (точку выхода не

считать.)

А) (0,5;1;1) Б) (0,5;0;1) В) (0,5;0;0,75) Г) (0,5;1;0)

Д) ни одно из перечисленных

Ответы и краткие решения 11–12 класс

1. Ответ А. lg2013²− 2lg2013 = 2lg2013 − 2lg2013 = 0.

2. Ответ Г. a₄= 3 + 3 · 671 = 3 + 2013 = 2016.

3. Ответ Б. Имеем f(x) = f((x + 1) − 1) = (x + 1)²− 3(x + + 1) + 1 = x²− x − 1.

4. Ответ Б. sin²x+2cosx−2 = 0 ⇐⇒ (1−cosx)²= 0 ⇐⇒

cosx = 1, это уравнение на данном отрезке имеет ровно 1 корень.

5. Ответ Б. Так как , то t_n– трехзначное, если

200 ≤ n²+ n < 2000. Трехзначные треугольные числа: t₁₄,..., t₄₄.

6.Ответ А. f(x) = 2 + sin²x + 2cosx − 2 = 2 − (1 − cosx)², f_min= f(π) = −2, f_max= f(0) = 2.

7.Ответ В. Четные числа не являются искомыми ввиду гипотезы Гольдбаха:-) (Найдите представления чисел 96 и 98!). Если сумма двух простых чисел нечетна, то одно из них равно 2. Проверим, что 99 − 2 простое, а 97 − 2 = 95 составное. Значит, 97 не представимо в виде суммы двух простых чисел.

8.Ответ Г. Количество благоприятных исходов 4·3·2, а общее число исходов 900.

9.Ответ Д. Ответ: 0. В _△ABD находим

. Поскольку AB+CD =

= BC + DA, имеем BM = BN, т.е. M ≡ N.

10. Ответ А. Применяя теорему Фалеса, последовательно найдем где точки M^′и N^′

середины AP и BP; кроме того. Тогда S_PNM: S_ABC=

11. Ответ Г. Фигура состоит из точек между двумя квадратами |x| + |y| = 1 и |x| + |y| = 2, следовательно, её площадь (2√2) 2 − √22 = 6.

12. Ответ Г. Он равен коэффициенту перед x³в стандартной форме многочлена (x³+ 1)⁶(1 + x)³. После раскрытия скобок многочлен примет вид

(1+6x³+Ax⁶)(1+3x+3x²+x³) = (1+3x+3x²+x³)+6x³(1+

+ 3x + 3x²+ x³) + Ax⁶(1 + 3x + 3x²+ x³), где A – многочлен. Следовательно, степень перед x³равна 7.

13. Ответ Г. Очевидно, x = 0 е решение за всяко m. Пусть

. При x = 0̸ данное неравенство равносильно нера-

венству 2m²≤ f(x). Так как f_min= 2, имеем, что m²≤ 1.

14. Ответ Б. Применим сравнения 2013 ≡ −2( mod 13), 2⁶≡

≡ −1( mod 13). Тогда получим 2013²⁰¹³≡ (−2)²⁰¹³≡ −(2⁶)³³⁵· 2³≡ ≡ 8( mod 13).

15. Ответ Д. Обозначим дельтоид ABCD, тогда AB = BC =

= √5 и AC × BD = O. Имеем BO²= AB²− AO²= 5 − 4 = 1.

Следовательно DO = 3, откуда AD = √2²+ 3²= √13.

16. Ответ А. Данное число в системе по основанию 4, должно иметь наибольшее количество цифр 3 (и если в записи есть другие числа, то они должны стоять сначала). Кроме того, 2013₄= 135 = = 45·3, означает, что ищется

17. Ответ В. Проекции точек P и Q на стороны равносторонних треугольников делят их пополам, поэтому PQ вдвое больше стороны шестиугольника. Тогда _△NPQ состоит из четырех равносторонних треугольников, а шестиугольник – из шести таких же,

как и внешне построенные. Следовательно, искомое отношение 4:6.

18. Ответ Б. Центры единичных окружностей образуют равносторонний треугольник со стороной 2 и, следовательно, с радиусом описанной окружности . От этого радиуса необходимо вы-

честь радиус данных окружностей.

19. Ответ Г. .

20. Ответ Б. Обозначим DX = x. Тогда

y = 3AX²+BX²= 3(AD²+DX²)+BC²+CX²= 4x²−20x+200.

Минимум квадратного трехчлена 4x²− 20x + 200 достигается при x = 5/2 и равен 175.

21. Ответ В. Имеем x²+ y²= 2y ⇐⇒ x²+ (y − 1)²= 1, т.е.

второе уравнение представляет окружность с центром (0;1) и радиус 1. Синусоида и окружность пересекаются первый раз в начале координат и второй раз в (x₀;y₀) при некотором x₀∈ (0;1). Это потому, что в точке (0;0) синусоида является касательной к прямой y = x, затем растет как вогнутая функция, а нижняя дуга окружности касается прямой y = 0, затем растет как выпуклая функция; кроме того при x = 1 окружность выше синусоиды. Значит, при x > x₀две кривые не имеют общих точек, поскольку окружность проходит вые прямой, проходящей через точки (0;0) и (x₀;y₀), а синусоида ниже

этой прямой.

22. Ответ В. Числа 8, 88, 888 и 8888 не делятся на 16. Тогда по признакам деления на 16 и на 5 числа вида 888...88 не делятся ни на 5, ни на 16. Все числа, которые не делятся на 5 или 16, представимы в виде произведения одного из чисел 1, 2, 4, или 8 на число n, заканчивающееся на 1, 3, 7 или 9. По принципу Дирихле, любое число n заканчивающееся на 1, 3, 7 или 9 имеет кратное вида 111...11. Но тогда числа n, 2n, 4n и 8n имеют кратное вида 888...88. Таким образом, число 888...88 может быть кратно любому числу, которое не делится на 5 или 16. Имеем 2010 : 5 = 402 числа кратных 5, 2000 : 16 = 125 числа кратных 16 и 2000 : 80 = 25

чисел кратных 5 и 16. Ответ: 2013 − 402 − 125 + 25 = 1511.

23. Ответ Б. Так как y+z = 2√2 и yz = x²+2, то y и z корни

уравнения t²− 2√2t + x²+ 2 = 0, т.е. (t − √2)²+ x²= 0. Данное уравнение имеет решение только тогда, когда x = 0 и t_1,2= √2.

24. Ответ Б. Так как ресиси цифра и произведение двух других, это 4, 6, 8 или 9. Только 6 можно представить в виде суммы четырех различных меньших чисел, два из которых являются его множителями: 6 = 0+1+2+3 = 2×3. Тогда ресиси равно 6, а ремими и рефафа это 2 и 3(и действительно в таком порядке; редодо –

1, солдо – 0).

25. Ответ А.

Обозначим P = BE × AC. Так как _△AEP ∼ _△ACE (∠BEA = ∠ACE), то

_△AEP равнобедренный, а тогда Q является серединой AP. Обозначим x длинна стороны пятиугольника, а y – AQ.

Поскольку ∠BEC = ∠ACE, имеем CP = PE = x. Далее, из ра-

AC AE

венства _△AEP ∼ _△ACE, следует

26. Ответ Г. Пусть a ≤ b ≤ c. Тогда a > 4 (иначе bc = 2⁴3³: a трехзначно). При a = 6 имеем bc = 72, откуда b = 8, c = 9. Если a ≥ 8, то c = 9, но тогда b ≤ 6 – противоречие. Тогда единственная

возможная тройка цифр {6, 8, 9}.

27. Ответ В. Если считать, что каждая падающая капля имеет массу 1, то капля, попавшая на n-ю плитку, будет иметь массу 2ⁿ⁻¹. Это означает, что плитка, на которой остановилась m-я капля соответствует наименьшей степени двойки, содержащейся в двоичном разложении m. Так как 2013 = 11111011101₂, то капли будут

на 9 плитках.

ⁿ^{(n 1)}

28. Ответ Д. Pn = n + (1 + 2 + ··· + n − 1) = n²+ − .

Следовательно.

29. Ответ Г. Процедура описывает рекурсивное решение задачи о ханойских башнях (с минимальным числом перемещений). Это число T_nудовлетворяет рекуррентному соотношению: T₁= 1, T_n= = 2T_n−1 + 1. При всех натуральных n получим, что T_n= 2ⁿ− 1.

30. Ответ Б. Луч попадает в вертикальных прямые, проходящие через центры боковых граней, каждый раз поднимаясь на

0,25.

Ответы 11–12 класс

1	2	3	4	5	6	7	8	9	10
А	Г	Б	Б	Б	А	В	Г	Д	А
11	12	13	14	15	16	17	18	19	20
Г	Г	Г	Б	Д	А	В	Б	Г	Б
21	22	23	24	25	26	27	28	29	30
В	В	Б	Б	А	Г	В	Д	Г	Б

Материалы для подготовки к турниру

«Черноризец Храбр»

и другим математическим состязаниям и конкурсам

Тема 1. Текстовые задачи

Задача 1. Из книги выпал кусок, первая страница которого имеет номер 387, а номер последней записывается теми же цифрами

в каком-то другом порядке. Сколько листов в выпавшем куске?

Задача 2. Средний возраст одиннадцати футболистов — 22 года. Во время игры один из игроков получил травму и ушел с поля. Средний возраст оставшихся игроков стал 21 год. Сколько лет фут-

болисту, ушедшему с поля?

Задача 3. Арбуз весит 20 кг и содержит 99% воды. Когда он

усох, то стал содержать воды 98%. Сколько теперь весит арбуз?

Задача 4. Алёша и Боря вместе весят 92 кг, Алёша и Вова весят 91 кг, Боря и Вова — 95 кг. Сколько весят Алёша, Боря и Вова?

Задача 5. Куб склеен из 27 одинаковых кубиков. Сколько клея потребовалось на его склеивание, если на склеивание двух граней

требуется 1 г клея?

Задача 6. На дереве растет 49 апельсинов и 50 бананов. Разрешено срывать одновременно два фрукта. Если срывают два одинаковых фрукта, то вместо них мгновенно вырастает один банан. Если же срывают два разных фрукта, то вместо них мгновенно вырастает один апельсин. Через некоторое время на дереве остался один

фрукт. Что это за фрукт – банан или апельсин?

Задача 7. Плитка шоколада состоит из 35 квадратиков (7×5).

Ее ломают по прямым, которые делят квадратики до тех пор, пока не получат отдельных 35 квадратиков. Сколько раз нужно поделить

шоколадку?

Задача 8. Для нумерации страниц учебника потребовалось 411

цифр. Сколько страниц в учебнике?

Задача 9. Мальчик стреляет в тире. Он заплатил за 5 выстрелов. За каждое попадание он получает право сделать два дополнительных выстрела. Всего он сделал 17 выстрелов. Сколько раз он

попал в цель?

Задача 10. В магазине продается шоколад в виде букв английского алфавита. Одинаковые буквы имеют одинаковую цену, а разные — разную. Известно, что слово ONE стоит 6$, слово TWO сто-

ит 9$, а слово ELEVEN стоит 16$. Сколько стоит слово TWELVE?

Задача 11. В темной кладовой в беспорядке лежат ботинки: 10 пар черных и 10 пар коричневых. Сколько ботинок надо взять, чтобы среди них оказалась хотя бы одна пара (левый и правый ботинок) одного цвета? (В темноте нельзя отличить не только цвет

ботинка, но и левый от правого.)

Задача 12. Сколько раз в течение суток угол между часовой

и минутной стрелками равняется 90^◦?

Задача 13. (Задача Льюиса Кэрролла). В ожесточенном сражении при Трафальгаре 70% участников потеряли глаз, 75% – ухо, 80% – руку, 85% – ногу. Каков наименьший процент числа ветеранов,

лишившихся одновременно глаза, уха, руки и ноги?

Задача 14. 9 коров опустошили луг за 4 дня. Если бы на луг пустили не 9, а 8 коров, то они съели бы всю траву за 6 дней. Сколько

коров могли бы кормиться на лугу всё время, пока растет трава?

Задача 15. (Задача Л. Н. Толстого) Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором еще остался участок, скошенный на другой день одним косцом за один

день работы. Сколько косцов было в артели?

Решения

1. Номер последней страницы должен быть четным и больше

чем 387, поэтому он равен 738. Тогда количество выпавших листов

738 − 386

= 176.

2.Суммарный возраст всех футболистов до ухода травмированного футболиста 22 · 11 = 242 года, а после его ухода 21 · 10 = 210. Поэтому возраст ушедшего игрока 32 года.

3.Первоначально масса «сухого вещества» 20·0,01 = 2 кг. Тогда после усушки масса арбуза будет 2/0,02 = 10 кг.

4.Сначала найдите суммарный вес трех мальчиков. Зная суммарный вес и общий вес любых двух мальчиков, легко найти вес оставшегося мальчика. Ответ. Алёша — 44 кг, Боря — 48 кг, Вова — 47 кг.

5.У 27 кубиков 162 грани. Из них наружных — 9 · 6 = 54. Склеивается 108 граней, образующих 54 пары. Следовательно, по-

надобится 54 г клея.

6.Указание: четность числа апельсинов не меняется.

7.При любом разламывании плитки количество квадратиков увеличивается на 1. Чтобы получить 35 квадратиков, нужно разломать плитку 34 раза.

8.Для нумерации страниц учебника использовали: 9 однозначных чисел — 9 цифр; все двузначные числа — 90 чисел — 180 цифр. Всеми однозначными и двузначными числами занумеровано 99 страниц и на это ушло 189 цифр. Осталось 411−198 = 222 цифры, которые ушли на написание 222 : 3 = 74 трехзначных чисел. В учебнике 99 + 74 = 173 страницы.

9.Так как мальчик сделал 17 выстрелов, то он получил 17−5 = = 12 дополнительных патронов. Тогда число попаданий 12 : 2 = 6.

10. Возьмем два слова ELEVEN и TWO. Заберем из этих букв одну букву O, одну N и одну E. Тогда из оставшихся букв можно сложить слово TWELVE. Значит, оно стоит 16+9−6 = 19 долла-

ров.

11. Если взять 20 ботинок, то может оказаться, что они все на левую ногу: 10 левых коричневых и 10 левых черных. Покажем, что достаточно взять 21 ботинок. Выстроим ботинки парами. Тогда будет всего 20 пар. Взяв 21 ботинок, мы обязательно возьмем два

ботинка из какой-то пары, то есть всю её целиком.

12. За 1 сутки часовая стрелка сделает 2 оборота, а минутная 24. Таким образом, минутная стрелка обгонит часовую 22 раза. Но между каждыми обгонами часовая и минутная стрелка образуют

прямой угол дважды, значит, ответ 44 раза.

13. Из условия следует, что 30% участников не потеряли глаз, 25% не потеряли ухо, 20% остались с рукой и 15% остались с ногой. Значит, число участников, которые сохранили глаз или ухо, или ру-

ку, или ногу, не может превышать 30% + 25% + 20% + 15% = 90%. Следовательно, число ветеранов, оставшихся одновременно без гла-

за, уха, руки и ноги не меньше 10%. Причем, этот минимум может достигаться, только если упомянутые множества из 30%, 25%, 20% и 15% не пересекаются, т. е. каждый из них сохранил только одну

часть тела, а три другие потерял.

14. Пусть объем заполненного травой луга достаточен для x ежедневных норм одной коровы и ежедневно подрастает еще y таких

норм. Получим уравнения: x + 4y = 9 · 4, x + 6y = 8 · 6. Отсюда, y = 6. Так как за один день на лугу вырастает только 6 норм корма,

то постоянно кормиться на лугу могут не более 6 коров.

15. Если большой луг полдня косила вся артель и полдня полартели, то ясно, что в полдня пол-артели скашивает луга. Следо-

вательно, на малом лугу остался нескошенным участок в . Если один косец в день скашивает луга, а скошено было ,

то косцов было 8.

Тема 2. Числа

Задача 1. Докажите, что 1 + 2 + 2²+ ... + 2²⁰¹⁴не делится на

Задача 2. Вычислите наиболее рациональным способом (не ис-

пользуя калькулятор): .

Задача 3. Незнайка перемножил все числа от 1 до 100. Посчитал сумму цифр произведения. У полученного числа он снова посчитал сумму цифр, и так далее. В конце концов получилось од-

нозначное число. Какое?

Задача 4. Найдите стороны прямоугольника, у которого пери-

метр численно равен площади, а стороны — натуральные числа.

Задача 5. В клетчатом квадрате, разрезая по границам клеток, прорезали квадратную дырку (меньшего размера). Может ли

оставшаяся фигура состоять ровно из 250 клеток?

Задача 6. Докажите, что при любом натуральном n число

является составным.

Задача 7. Найдите сумму: 0,(1)+2,(3)+4,(5)+...+98,(99).

Задача 8. Выписали сто чисел: 1, 12, 123, ..., 123456789, 12345678910, 1234567891011, ..., 123...9899100. Сколько среди них

чисел, делящихся на 3?

Задача 9. Первая слева цифра десятизначного числа равна числу единиц в записи этого числа, вторая — числу двоек, третья — числу троек, четвёртая — числу четверок, ..., девятая числу девя-

ток, десятая – числу нулей. Найдите это число.

Задача, 10. Можно ли расставить на ребрах куба числа от 1 до 12 так, чтобы все суммы в вершинах (суммируются числа, стоящие на ребрах, выходящих из данной вершины) были равны?

Задача 11. По кругу расставлены цифры 1, 2, 3, ..., 9 в произвольном порядке. Каждые три цифры, стоящие подряд по часовой стрелке, образуют трехзначное число. Найдите сумму всех получен-

ных таким образом трехзначных чисел.

Задача 12. Пусть n = 999...9 (2014 девяток). Сколько девяток

в десятичной записи числа n²?

Задача 13. Вася поднимается по лестнице из 12 ступенек. За один шаг он поднимается либо на одну ступеньку, либо на 2. Сколь-

кими способами Вася может подняться по лестнице?

Задача 14. Какой может быть дробная часть числа a + b + c,

если — целая часть числа

x, наибольшее целое число, не превосходящее x; {x} = x − [x] — дробная часть числа x.)

Задача 15. Решите систему уравнений:  y + [z] + {x} = 3,5, x + [y] + {z} = 3,9,

z + [x] + {y} = 2.

Задача 16. Число 11...11 делится на 7. Докажите, что оно

делится и на 13.

Задача 17. В следующих, записанных на венгерском языке задачах на умножение, множители — однозначные, а произведения —

двузначные числа.

het · nyolc = otvenhat; hat · het = negyvenketto; hat · kilenc = otvennegy; hat · nyolc = negyvennyolc; ot · nyolc = negyven; nyolc · kilenc =?

Ответ запишите на венгерском языке.

Задача 18. Делители числа n = 2³3⁴5²упорядочены в возрастающем порядке: d₁= 1, d₂= 2, d₃= 3, d₄= 4 и т.д. Чему равно

d₅₂?

Задача 19. Найдите наиболее близкое целое число к . (n! = 1·2·3·...·n — произведение всех натуральных чисел от 1 до n включительно, n-факториал.)

Задача 20. Найдите пятую цифру после запятой следующей

суммы

записанной в десятичной форме.

Задача 21. В последовательности 1, 3, 7, ... первый член равен 1, а каждый следующий получается, если умножить предыдущий на 2 и к произведению прибавить 1. На какую цифру оканчи-

вается 2014-й член этой последовательности?

Решения

1.1+2+2²+...+2²⁰¹⁴= 1+2·(1+2)+2³(1+2)+2⁵(1+2)+ + ... + 2²⁰¹³(1 + 2). Все слагаемые кроме первого делятся на 3.

2.Обозначим. Тогда, значение выражения равно

3.100! делиться на 9. Значит, все полученные суммы цифр делятся на 9. Следовательно, в конце получилось число 9.

4.Пусть a и b стороны прямоугольника. Получим уравнение 2a+2b = ab. Оно равносильно уравнению (a−2)(b−2) = 4. Получим следующие решения: (4, 4), (3, 6), (6, 3).

5.Задача сводится к решению уравнения n²−m²= (n−m)(n+ + m) = 250 в натуральных числах. Но числа n − m и n + m имеют

одинаковую четность, поэтому данное уравнение не имеет целочис-

ленных решений.

6..

7.Имеем следующую цепочку равенств

0,(1) + 2,(3) + 4,(5) + ... + 98,(99) = (0 + 2 + 4 + ... + 98)+

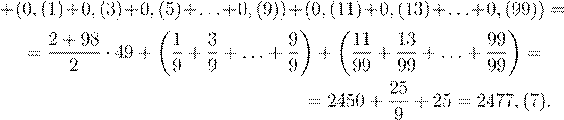
8.Обозначим a_iостаток от деления i-го числа на 3. Имеем, a₁=

= 1, a₂= 0, a₃= 0, a₄= 1, a₅= 0, a₆= 0, a₇= 1, ...(a_n₊₁остаток от деления суммы a_n+n+1 на 3). Итого получим, что на 3 не делятся

только 1-е, 4-е, 7-е, ...100-е число, всего 34 числа. Ответ: 66.

9.Полностью исключить перебор при решении этой задачи довольно трудно, но можно его сильно сократить. Заметим, например, что в числе не может быть больше одной пятерки, шестерки, семерки, восьмерки и девятки (а иначе было бы, скажем, 6 единиц и 6 двоек, и всего цифр было бы больше 10). Аналогично, четверок в числе – не больше 2, троек – не больше 3, двоек – не больше 5. Можно даже заметить, что семерок, восьмерок и девяток нет вовсе

(скажем, если бы была девятка, то было бы 9 каких-то одинаковых цифр. Нулями они быть не могут, ведь тогда и девятки в числе «не будет», а иначе в числе будут все цифры, из чего тоже легко вывести противоречие). Ну и самое простое – сумма всех цифр числа должна в точности равняться 10, поскольку общее количество цифр 10. Замечание. Ограничивая перебор еще сильнее, можно даже доказать единственность числа, удовлетворяющего условию задачи, но

это требует уже более сложных рассуждений. 2100010006.

10. Пусть S — сумма чисел при одной вершине. Тогда сумма чисел при всех вершинах равна 8S. С другой стороны, эта сумма равна 2(1 + 2 + ... + 12) = 13 · 12 = 156 (суммируем числа при всех ребрах, причем каждое ребро должно быть учтено дважды). Так как уравнение 8S = 156 не имеет целочисленных решений, то

расставить числа указанным способом невозможно.

11. Каждая цифра n будет присутствовать в разряде сотен, десятков и единиц, поэтому она дает в общую сумму вклад (1 + 10 +

100)·n = 111n. Тогда искомая сумма 111·(1+2+3+...+9) = 4995.

Таким образом, в десятичной записи числа n²содержится 2013 де-

вяток.

13. Обозначим a_n— число способов подняться на n-ю ступеньку. Имеем a₁= 1, a₂= 2 (на вторую ступеньку можно подняться сделав один шаг в две ступеньки, или два шага по одной). Так как на n + 2-ю ступеньку можно подняться, сделав шаг, с n-й, или с n + 1 ступеньки, то a_n₊₂= a_n₊₁+ a_n. Данным рекуррентным соотношением задается последовательность чисел Фибоначчи. Следует заметить, что число способов подняться по лестнице равно a₁₃. Последовательно вычисляя, получим a₁₃= 233.

14. Имеем, что , где

m, n, k ∈ Z. Сложив равенства, получим . В

зависимости от четности числителя {a + b + c} может равняться 0 или .

15. Сложив все уравнения, получим, что 2(x + y + z) = 9,4, откуда x + y + z = 4,7. Теперь сложим первое и второе уравнения: x + y + z + [y] + {x} = 7,4 =⇒ [y] + {x} = 2,7. Аналогично,

складывая первое уравнение с третьим и второе с третьим, получим:

[x] +{z} = 1,2; [z] + {y} = 0,8. Из этих уравнений следует, что



[x] = 1, {x} = 0,7,

 [y] = 2, {y} = 0,8,

[z] = 0, {z} = 0,2.

Значит, x = 1,7, y = 2,8, z = 0,2.

16. Докажем критерий: число 11...11 делится на 7 тогда и только тогда, когда n делится на 6. | {z } n единиц

Числа 1, 11, 111, 1111,11111 на 7 не делятся, а число 111111

делится на 7.

Пусть n = 6q + r, где r = 0, 5. Тогда

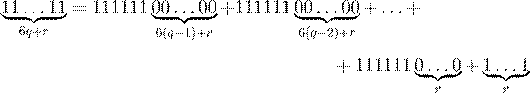Все слагаемые кроме последнего делятся на 7, а последнее де-

лится на 7 только при r = 0.

.^..6, а

Таким образом, еслиделится на 7, тогда n

.^..111111. Учитывая, что 111111 = 3 · 7 · 11 · 13 · 37, получим

число A

.^..13.

17. Можно предположить, что сочетание венгерских букв ven на русском языке означает «дцать» (например, двадцать пять,

тридцать). Тогда negyven заканчивается на 0.

Введем обозначения a = het, b = nyolc, c = ot, d = hat, e =

negy, f = ketto, g = kilenc.

Тогда условие можно записать следующим образом:

Требуется найти b · g.

Из последнего условия получим, что одно из чисел b или c четное, а другое равно 5. Если b = 5, то из первого условия d или 0, или 5, чего быть не может. Тогда c = 5, а b — четное. Из первого же

условия a · b = 5d, получим, что b > 5. Тогда b или 6, или 8.

Если b = 6. То из первого условия a · 6 = 5d находим, a = 9, d = 4. Тогда из второго уравнения e = 3, f = 6, а третье примет

вид 4 · g = 53. Получим, что решений нет.

Пусть b = 8. Тогда из первого условия a·8 = 5d находим, a = 7, d = 6. Из второго уравнения e = 4, f = 2, а третье примет вид

6 · g = 54. Получим, что g = 9. Убеждаемся, что четвертое и пятое уравнения верны. Таким образом, nyolc·kilenc = b·g = 8·9 = 72 =

hetvenketto.

18. Упражнение: докажите, что у числа число

делителей равно (α₁+ 1)(α₂+ 1) · ... · (α_s+ 1).

Тогда у данного числа (3 + 1)(4 + 1)(2 + 1) = 60 делителей. Заметим, что если число d_kявляется k-м делителем числа n (если упорядочить делители по возрастанию), то число -м делителем с конца. Значит, . Имеем, d₅= 5, d₆= 6, d₇= 8, d₈= 9, d₉= 10. Тогда d₅₂= 2²3⁴5.

19. Сокращая дробь на 2012!, получим

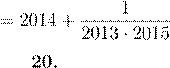. Значит, ответ 2014.

Но 10! = 2·5·3·4·6·7·8·9·10 > 10·10·40·70·10 = 28·10⁵> 10⁶, поэтому пятая (и даже шестая) цифра после запятой равна 9.

21. При ⁿ> 2 имеем, что a_n= 2a_n−1 + 1. Значит, a_n+ 1 =

= 2(a_n−1 +1) = 2²(a_n−2 +1) = 2³(a_n−3 +1) = ... = 2ⁿ⁻¹(a₁+1) = 2ⁿ. Следовательно, a_n= 2ⁿ− 1. Последовательность последних цифр числа 2ⁿпериодическая (2, 4, 8, 6, 2, 4, ...) с периодом 4. Число 2²⁰¹⁴= 2^503·4+2оканчивается на ту же цифру, что и 2²= 4. Тогда, a₂₀₁₄оканчивается на 3.

Тема 3. Принцип Дирихле

Принцип Дирихле: если в N клетках не менее N +1 кроликов,

то в какой-то клетке сидят хотя бы 2 кролика.

Обобщённый принцип Дирихле: если в N клетках не менее kN + 1 кроликов, то хотя бы в какой-то клетке сидит не менее

чем k + 1 кролик.

Задача 1. В школе 400 учеников. Докажите, что хотя бы двое

из них родились в один день года.

Задача 2. В классе 30 учеников. В диктанте Вова сделал 13 ошибок, а остальные ученики — меньше. Докажите, что по крайней

мере три ученика сделали ошибок поровну.

Задача 3. В клетках таблицы 3×3 расставлены числа -1, 0, 1. Докажите, что какие-то две из 8 сумм по всем строкам, всем столб-

цам и двум главным диагоналям будут равны.

Задача 4. Докажите, что существует степень тройки, оканчи-

вающаяся на 001.

Задача 5. На координатной плоскости отмечено 5 целочисленных точек (обе координаты каждой точки — целые числа). Докажите, что середина хотя бы одного из отрезков, соединяющих какие-то

две из этих точек, также является целочисленной точкой.

Задача 6. Докажите, что равносторонний треугольник нельзя

покрыть двумя меньшими равносторонними треугольниками.

Задача 7. Плоскость раскрашена в 2 цвета: черный и белый (причем имеется хотя бы одна белая и хотя бы одна черная точка). Докажите, что: а) найдутся две точки одного цвета на расстоянии 1 метр; б) найдутся две точки разного цвета, расстояние между которыми 1 метр.

Задача 8. Цифры 1, 2, ..., 9 разбили на три группы. Докажите,

что произведение чисел в одной из групп не меньше 72.

Задача 9. Каждая клетка таблицы 2015 × 2015 покрашена в один из 2014 цветов. За ход можно взять строку или столбец и, если там есть две клетки одного цвета, перекрасить эту строку или столбец в этот цвет. Всегда ли можно за несколько ходов покрасить

всю таблицу в один цвет?

Задача 10. Докажите, что среди любых 10 целых чисел найдется несколько рядом стоящих (возможно одно), сумма которых

делится на 10.

Задача 11. Даны 7 отрезков. Длина каждого больше 10 см и меньше 1 м. Докажите, что из каких-то трех можно составить

треугольник.

Задача 12. Дано 11 различных натуральных чисел, не больших 20. Докажите, что из них можно выбрать два числа, одно из которых

делится на другое.

Замечание. Данную задачу можно сформулировать в общем виде. Если из множества {1, 2, 3, ..., 2n} выбрать любые n + + 1 число, то среди них найдутся два таких числа, что одно делит

другое.

Задача 13. Одиннадцать вершин правильного 25-угольника отмечены красным цветом. Обязательно ли найдутся три отмеченные точки, которые являются вершинами некоторого равнобедренного

треугольника?

Задача 14. Докажите, что в каждом девятиугольнике есть па-

ра диагоналей, угол между которыми меньше 7^◦.

Задача 15. В танцевальном зале находятся 15 мальчиков и 15 девочек, расположенных в двух параллельных рядах, так что образуется 15 танцевальных пар. Получилось так, что разница между ростом мальчика и ростом девочки в каждой паре не превосходит 10 см. Докажите, что если расположить мальчиков и девочек в параллельные ряды по увеличению роста, также получится, что разница в росте у мальчика и девочки в каждой новой паре не будет превы-

шать 10 см.

Решения

1.В качестве «клеток» выступают дни в году (их не более 366),

а в качестве «кроликов» школьники.

2.Каждый из остальных 29 учеников сделал не более 12 ошибок. Разобьём их на 13 групп по числу сделанных ошибок (от 0 до 12). (В некоторых группах учеников может и не быть). Если бы в каждой группе оказалось не более двух учеников, то во всех группах вместе

было бы не более 26 учеников, а их 29. Значит, хотя бы в одной

группе учеников больше двух.

3.Эти суммы могут принимать лишь 7 разных значений: от –3

до 3.

4.Если 3^mи 3ⁿ— степени тройки, дающие один и тот же остаток при делении на 1000, то 3^m− 3ⁿ= 3ⁿ· (3^m⁻ⁿ− 1) делится на 1000 (мы считаем для определенности, что m > n).

5.Заметим, что середина отрезка с концами в точках (a, b) и (c, d) имеет вид .Для координат любой целочислен-

ной точки есть четыре возможности: (Ч, Ч), (Ч, Н), (Н, Ч), (Н, Н). Здесь Ч обозначает четную координату, а Н — нечетную. Так как точек 5, то есть, по крайней мере, две точки, которые имеют одинаковый вид — они то и будут искомыми.

6.Докажите, что меньший равносторонний треугольник покры-

вает не более одной вершины.

7.Рассмотрим на плоскости равносторонний треугольник со стороной 1 метр. Так как вершин 3, а цвета 2, то какие-то 2 вершины окрашены в один цвет. б) По условию есть хотя бы одна белая точка

A и хотя бы одна черная точка B. Возможны три случая.

1.Если AB = 1, то точки A и B искомые.

2.Если AB < 1, то проводим окружности с центрами в точках A и B радиуса 1 и получим точку пересечения окружностей C. Или

пара A, C или пара B, C является искомой.

3.Если AB > 1, то на отрезке AB строим точки A_iтак, что A_iA_i₊₁= 1 (A = A₀, i = 0, 1, ..., n −1). Если A_i₊₁и A_iокрашены в разные цвета, то пара A_i, A_i₊₁искомая. Если все A_iодного цвета, то рассматриваем пару A_n, B и приходим или к первому, или ко второму случаю. Число n выбирается так, что A₀A_n< AB, а

A0An+1 > AB.

8.Произведение чисел во всех группах равно 9! = 362880, а 71³= 357911.

9.Возьмем любую строку. Так как цветов 2014, а клеток в строке — 2015, есть по крайней мере две клетки одного цвета. Значит, мы можем перекрасить всю строку в этот цвет. Воспользуемся этим и покрасим каждую строку в какой-нибудь цвет. Теперь имеется 2015 строк, покрашенные в 2014 цветов. Значит, по крайней мере две строки покрашены в один цвет (допустим, красный). То есть, в любом столбце есть две красные клетки. Покрасим все столбцы в красный цвет — все клетки таблицы будут покрашены в один цвет.

10. Рассмотрите 10 сумм: x₁, x₁+x₂, ..., x₁+x₂+...+x₁₀и их остатки при делении на 10. Если один из остатков ноль, то искомая сумма найдена. В противном случае, две суммы дают одинаковый

остаток от деления на 10, тогда их разность делится на 10.

11. Расположим отрезки по величине: a₁6 a₂6 ... 6 a₇. Из отрезков можно составить треугольник тогда и только тогда, когда найдется такое k, что a_k+ a_k₊₁> a_k₊₂. Предположим, утверждение задачи неверно. Значит, a_k+a_k₊₁6 a_k₊₂(k = 1, 2, ..., 5.) Но тогда

a₃> 20, a₄> 30, ..., a₇> 130 см. Противоречие.

12. Разбейте числа от 1 до 20 на 10 наборов, в каждом из которых в любой паре чисел одно делится на другое: {11}, {13}, {15}, {17}, {19}, {1,2,4,8,16}, {3,6,12}, {5,10,20}, {7,14}, {9,18}.

13. 25 вершин разбиваются на 5 групп, каждая из которых представляет собой вершины некоторого правильного пятиугольника. Так как отмеченных точек 11, то найдется правильный пятиугольник, у которого отмечены не мене трех вершин. Но всякие 3 вершины правильного пятиугольника являются вершинами некоторого

равнобедренного треугольника.

14. У девятиугольника диагоналей. (Упражнение: до-

n(n − 3)

кажите, что число диагоналей n-угольника равно .) Через

произвольную точку плоскости проведем 27 прямых параллельно этим диагоналям. Получим 54 угла. Если каждый из этих углов не меньше 7^◦, то их сумма не меньше 54 · 7^◦= 378^◦> 360^◦, что невозможно.

15. Пусть P₁, P₂, ..., P₁₅— пятнадцать исходных пар. Расположим теперь мальчиков по росту: a₁6 a₂6 ... 6 a₁₅; и девочек тоже расположим по росту: b₁6 b₂6 ... 6 b₁₅.

Предположим, что в какой-то паре разница в росте превышает 10 см: a_k− b_k> 10.

Тогда для мальчиков ростом a_k,a_k₊₁,...,a₁₅и для девочек ростом b₁,b₂,...,b_kтакже выполняется условие a_i− b_j> > 10. Рассмотрим исходные пары, в которые попали дети ростом b₁,...,b_k,a_k,a_k₊₁,...,a₁₅. По принципу Дирихле, двое из этих 16 детей попадут в одну пару. Тем самым хотя бы в одной из исходных пар разница между ростом мальчика и ростом девочки должна быть больше 10 см.

Тема 4. Геометрия

Задача 1. Арбуз разрезали на 4 части и съели. Получилось 5

корок. Как это могло быть?

Задача 2. На прямоугольном куске хлеба лежит кружок колбасы. Докажите, что этот бутерброд можно разрезать одним прямолинейным разрезом на два так, чтобы и хлеб, и колбаса разделились

поровну.

Задача 3. Одним прямолинейным разрезом разделите данные шестиугольники на две равновеликие части (имеющие одинаковую

площадь).

Задача 4. Можно ли из пяти одинаковых прямоугольников с

периметром 10 составить один прямоугольник с периметром 22?

....................

....

...

...................................... ................................................^M....................................................................................................................................................................................................................................

...............

...................

.....

.................

....

.............................

Задача 5. ABCD — квадрат. ..........................................

...................

..........................

Треугольники AMD и AKB — рав- .....................

..............................

носторонние. Верно ли, что точкиM и K лежат на одной прямой? C, K .................................................................................................................................................................................................

A D

Задача 6. Найдите сумму внешних углов при вершинах выпук-

лого n-угольника, взятых по одному при каждой вершине.

Задача 7. Существует ли выпуклый 2014-угольник, у которого

все углы выражаются целым числом градусов?

Задача 8. Докажите, что у выпуклого многоугольника не может быть более трех острых углов.

Задача 9. В круг радиуса 1 вписан пятиугольник. Докажите, что сумма длин его сторон и диагоналей меньше 17.

........................................................................

...... ......

...................................................

......................................................

..................................................... O

Задача 10. ABCD — прямоуголь- A J ...................B ник, I — середина AD, J — середина

I ..

AB. Каково отношение площадей четы-

рехугольников AIOJ и BCDO? D^.C

Задача 11. Из четырех спичек длины 1 сложили прямоугольный треугольник, предварительно разломав одну из спичек на две части. Чему может равняться площадь такого треугольника?

.... ........... ..............................................................................

. ...................^........

....... ......................^...........................

... ........................^............................

........................^.........

.... ..............................^................................

......................^..........

.................^............................

.................... .............

.....................

............... .....................

...........................

...

равные части.

Задача 13. Из трех равных квадра-

тов составлен прямоугольник. Из верши-

B.......

..........^......................................................................................................................................................................................

..........................................................................................................

.................................................................................................................

........................................................................................................

Задача 12. В квадрате ABCD про- B..................C ведены отрезки CE и CF, где E — середина AB, F — середина AD. Докажите, E .. что CE и CF делят отрезок BD на три

.. .

...............

ны B его проведены три отрезка BE, BF

и BD. Чему равна сумма углов ∠AEB+ A E. F.. ..D.

∠AFB + ∠ADB?

Задача 14. Дан равнобедренный треугольник ABC c углом при вершине B, равным 20^◦. Докажите, что а) AB < 3AC; б) AB > > 2AC.

Задача 15. На сторонах треугольника ABC внешним образом построены правильные треугольники A₁BC, AB₁C и ABC₁. Докажите, что AA₁= BB₁= CC₁.

Задача 16. Деревни A, B и C расположены в вершинах рав-

ностороннего треугольника. В деревне A живут 100 школьников, в деревне B — 200, в деревне C — 300. Где нужно построить школу, чтобы суммарное расстояние, проходимое всеми школьниками, было бы как можно меньше?

Решения

1. Подсказка: у одного куска должно быть 2 корки.

2. Необходимо провести разрез по прямой, соединяющей центр

круга и центр прямоугольника. Вопрос: что если центры совпадают? 3. Посмотрите на ответ и дайте его обоснование.

4. Можно. Первый пример. Поставьте вертикально 3 прямоугольника размера 3 × 2, а под ними расположите горизонтально два таких же прямоугольника. Второй пример. Выложим вертикальной стопкой 5 прямоугольников с длинной x, а высотой y.

Тогда, x + y = 5, x + 5y = 11. Отсюда x = 3,5, y = 1,5.

5. Проведем отрезки MK и MC B C

............................

и докажем, что ∠KMC — развер- .................................. ......

.... ..... ^.....^...^..^..^..^....................................................^{.....................}........................................... K ........................................................^.... .............................

равностороннего треугольника рав-нутый. Так как сторона каждого ............................................................................................................................................................................................................

на стороне квадрата, A D то треугольники KAM и MDC — равнобедренные с основаниями KM и MC соответственно. Заметим, что ∠KAM = ∠KAB + ∠BAM = 60^◦+ 30^◦= 90^◦, a ∠MDC = 30^◦. Следовательно, ∠KMA = 45^◦, ∠DMC = 75^◦. То есть, ∠KMC = ∠KMA+∠AMD +∠DMC = 45^◦+60^◦+75^◦= 180^◦, значит, точки C, M и K лежат на одной прямой.

6.Пусть дан выпуклый n-угольник A₁A₂...A_n. Внешний угол

при вершине A_iравен 180^◦− ∠A_i. Тогда сумма внешних углов при всех вершинах 180^◦·n−(∠A₁+∠A₂+...+∠A_n) = 180^◦·n−180^◦· (n − 2) = 360^◦.

7.Предположим, что такой многоугольник существует. Каждый угол этого многоугольника не превосходит 179^◦. Значит, сумма его углов не превосходит 2014 · 179^◦= 360506^◦. С другой стороны, известно, что сумма углов любого выпуклого 2014-угольника равна 2012·180^◦= 362160^◦. Полученное противоречие показывает, что такого многоугольника не существует. Заметим, что приведенное рассуждение можно существенно упростить, если воспользоваться тем, что сумма внешних углов любого выпуклого многоугольника равна

360^◦.

8.Пусть острых углов в треугольнике k > 3, тогда сумма тупых углов (обозначим ее S) равна сумме всех углов треугольника без суммы острых углов; если острые углы заменить на прямые, а тупые на развернутые, то получим оценку 180^◦(n−k) > S > 180^◦(n−2)−90^◦k. Для k получим неравенство 180^◦(n−k) > 180^◦(n−2)−90^◦k, решая которое получим k < 4. Замечание. Существуют многоугольники без острых углов (например, правильный шестиугольник), с одним острым углом (постройте семиугольник, используя правильный шестиугольник), с двумя и с тремя острыми углами (остроугольный

треугольник).

9.Периметр пятиугольника не превосходит длины окружности равной 2π. У пятиугольника ровно 5 диагоналей, каждая из которых не больше 2 (диаметра). Тогда сумма сторон и диагоналей не превосходит 2π + 5 · 2 < 17.

10. Проведем отрезки IJ и BD. То-

гда треугольник △AIJ ∼ △CBD, а △OIJ ∼ △OBD с коэффициентом подобия . Следовательно, отношение площадей указанных четырехуголь- D C

ников равно .

11. Пусть одну из спичек разломали на части с длинами x и 1−x. Гипотенуза не может состоять только из целых спичек (длина 1 слишком мала, а 2 — слишком велика). Поэтому длина гипотенузы равна 1 + x. Значит, один из катетов имеет длину 1, а другой 2 − x. Из теоремы Пифагора следует равенство 1+(2−x)²= (1+x)². Это уравнение имеет единственный корень, равный 2/3, следовательно

треугольник имеет стороны 5/3, 1 и 4/3, а его площадь равна 2/3.

12. Точки пересечения отрезков CE и CF с диагональю BD являются точками пересечения медиан треугольников ABC и ADC. Поскольку медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины, а треугольники ABC и ADC равны, то расстояния между точками пересечения медиан равно расстоянию от них до вершин B и D.

13. Сделаем дополнительное постро-

ение. Проведем отрезки KD и BK, как показано на рисунке. B...........................C

...................._...^...^...^....^................................._...._............._................................................_...._...._...._................................^.....^....^....^....^....^....^...^...^..^..^..^..^..^..^..^..^..................^..^..^..^..^..^..^..^..^..^...^..^..^..^..^..^........................................

..........................................................................................................

..................................................................................................................

............................................................................................................

...........................................................E.........................................................

.........................................

...................................

..................................

...

.............................

............................................

...................................

Имеем, что угол ∠AFB = ∠KDA, тогда

∠AFB+∠ADB = ∠KDB. Но треуголь- A..D

ник △BDK — равнобедренный прямо- .

. угольный, BK = KD. Значит, ∠KDB = K

45^◦. Таким образом, ∠AEB + ∠AFB +

∠ADB = 45^◦+ 45^◦= 90^◦.

14.

а)б)A C

а) Повернем треугольник ABC вокруг вершины B на 20^◦два раза. Получим, что △BCA₂равносторонний. Тогда AB = BC = CA₂< CA + AA₁+ AA₂= 3AC.

б) Отложите на стороне AB отрезок AE, равный основанию AC. Имеем, что ∠A = ∠ACB = ¹⁸⁰◦ ₂− ²⁰◦ = 80^◦. Треугольник ACE — равнобедренный, следовательно, ∠ACE = 50^◦. Значит, ∠ECB =

= 30^◦. Так как ∠ECB > ∠B, то EB > EC = AC, а AB = AE + EB = AC + EB > 2AC.

15. При повороте вокруг точки C на угол 60^◦точка A переходит в B₁, а точка A₁— в B. Поэтому отрезок AA₁переходит в отрезок B₁B.

16. В деревне C. Если построить ее в любой другой точке X, то при переносе ее в C суммарное расстояние, проходимое школьника-

ми, изменится на 100AX + 200BX + 300CX − 100AC − 200BC = = 300CX−100(AC−AX)−200(BC−BX) > 0, то есть уменьшится,

так как AC − AX < CX, BC − BX < CX.

Тема 5. Комбинаторика

Комбинаторика— это раздел математики, изучающий методы

решения задач на подсчет числа различных комбинаций.

В комбинаторике есть два важных правила, часто применяемых

при решении комбинаторных задач.

Основные правила комбинаторики

Правило произведения. Пусть требуется выполнить одно за другим какие-то k действий, причем 1-е действие можно выполнить n₁способами, 2-е – n₂способами и т. д. до k-го действия, которое можно выполнить n_kспособами, причем количество способов выполнить каждое действие не зависит от того, какими были предыдущие действия. Тогда все k действий можно выполнить n₁· n₂· ... · n_k

способами.

Правило суммы. Пусть требуется выполнить одно из какихлибо k действий, взаимно исключающих друг друга. Если 1-е действие можно выполнить n₁способами, 2-е – n₂способами и т. д. до k-го действия, которое можно выполнить n_kспособами, то выполнить одно из этих k действий можно (n₁+ n₂+ ... + n_k) способами.

Основные понятия комбинаторики

Перестановки n элементов. Пусть дано множество из n различных элементов. Требуется расположить эти n элементов в определенном порядке. Все такие размещения n элементов называются перестановками. Число перестановок n элементов равно P_n= n!.

Упорядоченные множества, в которых элемент a₁повторяется n₁раз, a₂повторяется n₂раз, ..., a_kповторяется n_kраз называются перестановками с повторениями. Число всех переста-

новок с повторениями равно, где

n = n₁+ n₂+ ... + n_k.

Размещения из n элементов по k. Пусть дано множество

из n элементов, из которого требуется выбрать упорядоченное подмножество, состоящее из k различных элементов (то есть выбрать первый элемент, второй элемент и так далее вплоть до k-го). Каждый способ это сделать называется размещением без повторений. Способы считаются различными, если хотя бы на одном месте в них стоят различные элементы. Число размещений без повторений рав-

но.

−

Если в выбираемом упорядоченном k-элементном подмножестве элементы могут повторятся, то такие подмножества называются размещениями с повторениями. Число размещений с повторениями

равно .

Сочетания из n элементов по k. Пусть из n-элементного

множества требуется выбрать неупорядоченное подмножество, состоящие из k различных элементов. Каждый способ это сделать называется сочетанием из n элементов по k. Различные сочетания отличаются друг от друга только составом, но не порядком элемен-

тов. Число сочетаний из n элементов по k равно.

Допустим, что имеется n различных типов элементов. Тогда комбинация из k элементов, при условии, что элементы одного типа могут встречаться несколько раз и порядок элементов в комбинации не важен, называется сочетанием с повторениями из n элемен-

тов по k. Число сочетаний с повторениями равно

Число беспорядков.

Задача о рассеянной секретарше. Секретарше нужно отправить

n различных писем по n различным адресам. Она подписывает конверты и случайным образом вкладывает письма в конверты. Сколько существует способов разложить письма по конвертам так, чтобы ни одно письмо не дошло до адресата (т.е. каждое письмо попадает

в чужой конверт).

Данная задача является (литературным) вариантом широко известной комбинаторной задачи о беспорядках. Перестановка (a₁,a₂, ..., a_n) чисел 1, 2, ..., n называется беспорядком, если для любого i a_i≠ i. Число беспорядков обозначается !n (или D_n). Для

числа беспорядков существует рекуррентные соотношения: 1) !1 = 0, !2 = 1, !(n + 2) = (n + 1) · (!(n + 1)+!n);

2) !1 = 0, !(n + 1) = (−1)ⁿ⁺¹+ (n + 1)·!n.

Данные рекуррентные соотношения похожи на соотношения, позволяющие рекуррентно вычислять факториалы. В связи с этим обстоятельством число беспорядков !n иногда называют субфак-

ториалом.

Задача 1. Докажите все формулы для числа перестановок, числа размещений и числа сочетаний.

Задача 2. Сколько путей идущих

по стрелкам ведут из A в D?

Задача 3. Сколькими способами 15 пронумерованных бильярд-

ных шаров могут распределиться по шести лузам?

Задача 4. 1) Сколькими способами Дима сможет покрасить пять елок в серебристый, зеленый и синий цвета, если количество краски у него неограничено, а каждую елку он красит только в один

цвет?

2) У Димы есть пять шариков: красный, зеленый, желтый, синий и золотой. Сколькими способами он сможет украсить ими пять елок,

если на каждую требуется надеть ровно один шарик?

3) А если можно надевать несколько шариков на одну елку (и

все шарики должны быть использованы)?

Задача 5. 1) В заборе 20 досок, каждую надо покрасить в синий, зеленый или желтый цвет, причем соседние доски должны быть покрашены в разные цвета. Сколькими способами это можно сделать? 2) А если требуется еще, чтобы хоть одна из досок обязательно

была синей?

Задача 6. На полке располагаются 10 книг. 1) Сколько существует различных способов расположения 10-ти книг? 2)Сколько существует различных способов расположения 10-ти книг, при которых две заранее отмеченных окажутся рядом? 3) Сколько существует различных способов расположения 10-ти книг, при которых две заранее отмеченных не стоят рядом? 4) Сколько существует различных способов расположения 10-ти книг, при которых три заранее

отмеченных окажутся рядом?

Задача 7. У людоеда в подвале томятся 25 пленников. 1) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин? 2) А сколько есть способов выбрать троих,

чтобы отпустить на свободу?

Задача 8. На полке стоит 12 книг. Сколькими способами можно

выбрать из них 5 книг, никакие две из которых не стоят рядом?

Задача 9. На полке стоят 10 книг. 1) Сколькими способами их можно переставить так, чтобы ни одна книга не осталась на месте?

б) А если на месте должны остаться ровно 3 книги?

Задача 10. Для каждого трехзначного числа берем произведение его цифр, а затем эти произведения, вычисленные для всех трехзначных чисел, складываем. Сколько получится? (Разумеется, если хотя бы одна из цифр числа – ноль, то и произведение равно

нулю.)

Задача 11. Каждую грань куба можно покрасить либо в чёрный, либо в белый цвет. Сколько различных кубов можно изготовить? (Два куба считаем различными, если их нельзя перепутать, как ни вращай.)

Задача 12. Сколько существует различных прямоугольников со сторонами, идущими по ли-

ниям сетки прямоугольника 6 × 8?

Задача 13. Сколько различных значений можно получить, расставляя всеми возможными способами скобки в выражении 2 : 3 : : 5 : 7 : 11 : 13 : 17 : 19 : 23 : 29?

Задача 14. На плоскости проведено n прямых так, что никакие 2 из них не параллельны и никакие 3 не пересекаются в одной точке. 1) Найти количество точек пересечения этих прямых; 2) На сколько частей делят плоскость эти прямые? 3) Сколько среди них

ограниченных частей и сколько неограниченных?

Задача15. Во скольких подмножествах множества {1, 2, 3, ..., 11} не найдется двух подряд идущих чисел (пустое подмножество тоже считаем)?

Задача16. По прямой в одном направлении на некотором расстоянии друг от друга движутся 2014 одинаковых шариков, а навстречу им движутся 2015 таких же шариков. Скорости всех шариков одинаковы. При столкновении любых двух шариков они разлетаются в противоположные стороны с той же скоростью, с какой двигались до столкновения. Сколько всего столкновений произойдет

между шариками?

Решения

2. В точку B можно попасть 6 способами (3 стрелки из A и 3 из C). Тогда количество путей из A в D, проходящих через B, равно

6 · 4 = 24. Еще имеется 3 · 3 = 9 путей из A в D, проходящих через C, но не через B. Тогда общее число путей равно 24 + 9 = 33.

3.Пронумеруем лузы числами от 1 до 6. Тогда каждому из 15 шаров можем поставить в соответствие любую из 6 луз. Таким об-

разом, шары могут распределиться по лузам спо-

собами.

4.1) Каждую из пяти елок можно покрасить в один из трех

цветов, поэтому всего различных способов существует 3⁵= 243. 2) На первую елку можно надеть любой из пяти шариков, на вторую елку — любой из оставшихся четырех, и так далее; всего получаем 5! = 120 способов. 3) Каждый из шариков можно надеть на любую

елку, поэтому в этом случае ответ — 5⁵= 3125.

5.1) Первую доску покрасим любым из трех цветов, а каждую следующую можно покрасить двумя способами в любой цвет кроме того, которым покрашена предыдущая доска. Таким образом, существует 3·2¹⁹различных раскрасок. 2) Существует всего 2 раскраски забора в зеленый и желтый цвета. В остальных 3 · 2¹⁹− 2 способах покраски хотя бы одна доска будет синего цвета.

6.1) 10!; 2) Свяжем две книги, которые должны стоять рядом. Получим 8 книг и связку. Их можно переставить 9! способами. Кроме того, можно переставить книги в связке 2! способами. Значит число различных расстановок книг равно 9!·2!; 3) 10!−2!·9! = 8·9! 4) 8! · 3!.

7.1) В первом случае важен порядок выбранных пленников. Поэтому на завтрак, обед и ужин людоед может выбрать трех пленни-

ков способами. 2) В данном случае порядок выбранных

пленных не важен. Значит, людоед может отпустить трех человек

на свободу способами.

8.Рассмотрим 7 оставшихся на полке книг. Между каждыми двумя соседними (и справа и слева от крайних) либо есть пустое место (от одной вынутой книги) либо нет. Набор пустых мест одно-

значно определяет комплект вынутых книг. Ответ:.

9.1) способами можем выбрать три книги, которые

стоят на месте, а остальные 7 книг можно переставить !7 способами. Таким образом, искомое число способов перестановки книг равно

!7 .

10. (1+2+...+9)·(0+1+...+9)·(0+1+...+9) = 45³. Если в левой части равенства раскрыть скобки, то в полученной сумме встретятся по одному разу произведения, соответствующие всем трехзначным числам (например, произведение 2·5·7, соответствующее числу 257, получится, когда мы из первой скобки возьмем двойку, из второй –

пятерку, а из третьей – семерку).

11. Все кубики с одной чёрной гранью неразличимы. Если две грани покрашены чёрной краской, а остальные — белой, то возможны две различные раскраски куба: одна, когда чёрной краской покрашены смежные грани, другая — когда противоположные грани. Покрасив ещё одну грань чёрной краской, получим снова две различные раскраски. Поменяв чёрную краску на белую и наоборот, получим аналогично ещё четыре различные раскраски. Всего получили 8 различных раскрасок куба двумя красками. Если к ним добавить раскраски куба одной краской (белой или чёрной), то по-

лучим всего 10 вариантов. Ответ: 10 вариантов.

12. Любой прямоугольник определяется парой горизонтальных и парой вертикальных сторон. Горизонтальные стороны можно вы-

брать способом, а вертикальные

способами. Значит, число прямоугольников равно 21 · 36 = 756.

13. При любой расстановке скобок данное выражение можно представить в виде дроби. Тогда, так как все данные числа –— простые, результат вычислений будет однозначно определяется тем, куда «попало» каждое из этих чисел: в числитель или в знаменатель. Очевидно, что независимо от расстановки скобок, число 2 попадает в числитель, а число 3 –— в знаменатель. Каждое из следующих чисел может «попасть» как в числитель, так и в знаменатель, например, при такой расстановке скобок 2 : (3 : 5)... число 5 окажется в числителе дроби, а если скобки поставить так (2 : 3) : 5... –— в

знаменателе.

Докажем, что существуют расстановки скобок, при которых каждое из чисел 5, 7, 11, 13, 17, 19, 23, 29 «попадает» как в числитель, так и в знаменатель, независимо от расположения остальных чисел. Для этого, например, разобьем все данные числа, начиная с числа 3, на группы следующим образом: каждая группа начинается с числа, которое должно «попасть» в знаменатель, и может содержать еще несколько (в том числе, и ноль) чисел, идущих следом за ним, которые все должны «попасть» в числитель. Эти группы заключаем в скобки и больше нигде скобок не ставим. Тогда первое число каждой группы попадет в знаменатель, так как на него непосредственно делится двойка, а остальные числа группы «попадут» в числитель, так как на них делится первое число из этой группы, «попавшее» в знаменатель. Таким образом, количество чисел, которые могут являться значением данного выражения при всех

возможных расстановках скобок, равно 2⁸= 256.

14. 1) Любые 2 прямые из n образуют ровно одну точку пересеn(n − 1)

чения. Поэтому, всего точек пересечения.

2) Предположим, что на плоскости уже проведены k прямых; проведем (k+1)-ю прямую и посмотрим, на сколько увеличится число частей, на которые прямые разбивают плоскость. (k +1)-прямая пересекается с уже имеющимися k прямыми в k точках, которые делят ее на k + 1 частей. Следовательно, (k + 1)-я прямая рассечет ровно k + 1 частей из всех имеющихся ранее частей плоскости. Так как каждую из этих частей она разбивает на две части, то после проведения (k + 1)-й прямой общее число частей увеличится на k + 1. Но если проведена только одна прямая, то плоскость разбивается ею на 2 части. Отсюда вытекает, что после проведения n прямых плоскость будет разбита на 2+2+3+...+n частей (от проведения второй прямой добавится еще 2 части, от проведения третьей — еще три, от проведения четвертой — еще четыре и т. д.). Следовательно, плоскость будет разбита на

частей. 3) Представим себе, что мы построили окружность, охватывающую все ограниченные части плоскости. Из этой окружности будет выходит 2n лучей, которые разделят окружность на 2n частей. Таким образом, количество неограниченных частей равно

2n. Следовательно, ограниченных частей будет .

15. Пусть A_n— количество подмножеств множества {1,2,...,n}, не содержащих двух подряд идущих чисел. Количество таких подмножеств, не содержащих число n, равняется A_n−1, так как в этом случае подмножества являются также подмножествами в {1,2,...,n−1}. Количество таких подмножеств, содержащих число n, равняется A_n−2, так как в этом случае подмножества при выкидывании числа n становятся подмножествами в {1,2,...,n − 2}.

Получаем равенство A_n= A_n−1 + A_n−2. Очевидно, A₁= 2, A₂= 3. Осталось последовательно вычислить A₃, A₄, ..., A₁₁. Получаем A₁₁= 233.

16. После столкновения шарики разлетаются с той же скоростью, поэтому ситуация не изменится. если мы разрешим шарикам при столкновении проскакивать друг сквозь друга, сохраняя скорость. Тогда каждый шарик, катящийся «справа », встретит по одному разу каждый из шариков, катящихся «слева», т.е. встреч будет

2014 · 2015.

Тема 6. Неравенства

Задача 1. В неравенствах

П > Р > О < Е < К < Т < И < Р > О > В > А > Н < И > Е

разным буквам соответствуют разные цифры, одинаковым — оди-

наковые. Какая цифра соответствует букве В?

Задача 2. Какое из чисел больше: или B =

= ?

Задача 3. Докажите, что 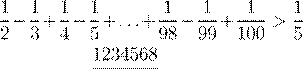. Задача 4. Что больше ?

Задача 5.Рассмотрим число . Докажите,

что оно 1) меньше ; 2) больше .

Задача, 6. Вещественные числа x и y таковы, что 0 6 x, y 6 1.

Докажите, что .

Задача, 7. Докажите неравенство: a⁸− a⁵+ a²− a + 1 > 0.

Неравенство о средних.

Пусть a₁, a₂, ..., a_nположительные числа.

Введем обозначения:

— среднее арифметическое чисел a₁, a₂, ..., a_n;

G_n= √ⁿa₁· a₂· ... · a_n— среднее геометрическое; — среднее гармоническое;

— среднее квадратическое.

Для любых положительных чисел a₁, a₂, ..., a_nсправедливо

неравенство:

min{a₁, a₂, ..., a_n} 6 H_n6 G_n6 A_n6 Q_n6 max{a₁, a₂, ..., a_n}, причем равенства достигаются, если только a₁= a₂= ... = a_n.

Следует выделить частный случай этого неравенства. Неравен-

ство Коши: пусть a, b > 0, тогда .

Задача 8. Докажите неравенство о средних для n = 2.

Задача 9. а) Для любого x > 0 справедливо неравенство x +

, причем равенство достигается если только x = 1. (Сформу-

лируйте аналогичное неравенство при x < 0.)

б) Пусть a·b > 0, тогда , причем равенство достигается если a = b.

в) Для любых чисел a и b имеет место. m

Задача 10.— правильная дробь. Какое из чисел ближе к n

m n единице: или ? n m

Задача 11. Докажите, что x⁴+ y⁴+ 8 > 8xy при любых x и y.

Задача 12. a, b, c, d — положительные числа. Докажите, что

Задача 13. Сумма трех положительных чисел a, b и c равна 1.

Докажите, что √4a + 1 + √4b + 1 + √4c + 1 < 5.

Задача 14. Докажите, что .

Задача 15. Докажите, что при всех a, b и c справедливо неравенство: a²+b²+c²> ab+bc+ac. При каких a, b и c оно превращается в равенство.

Задача 16. a³+ b³+ c³= 3abc, a ≠ b. Найдите a + b + c.

Решения

1. Имеем следующие цепочки неравенств: П>Р>О>В>А>Н; И>Т>К>Е>О. Но так как И<Р, то П>Р>И>Т>К>Е>О>В>А>Н.

Следовательно, В=2.

2. Домножим оба числа на 10. Тогда

. Так как знаменатель

второй дроби больше, то число 10B < 10A, значит, A > B.

Выясним это при положительных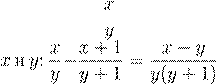. Следо-

вательно, все зависит от того, что больше: x или y. В данном случае

y > x и поэтому — большее из двух данных чисел.

5. Имеем, что. Обозначим B = 2 3 4 5

2) Оценка сверху доказывается аналогично.

6.Без ограничения общности можем считать, что x 6 y. Тогда

7.При a 6 0 неравенство, очевидно, верно. Если 0 < a < 1, то a⁸+ a²(1 − a³) + 1 − a > 0 (так как все слагаемые положительны). Если a > 1, то a⁵(a³− 1) + a(a − 1) + 1 > 0 ( первые два слагае-

мых неотрицательные, а последнее положительное). Таким образом,

неравенство верно при всех a.

10. Сравним числа . Вычтем из второго числа

первое, тогда (знак

неравенства строгий так как ). Таким образом, дробь к

единице ближе.

Задача 11.

= 8|xy| > 8xy.

12. Первый способ. Раскройте скобки и воспользуйтесь тем, что сумма двух взаимнообратных положительных чисел не меньше 2. Второй способ. Запишем неравенство в виде

. Последнее неравенство является неравенством

между средним арифметическим и средним гармоническим для

четырех чисел.

13. По неравенству Коши имеем√√4a + 1 = √(4a√+ 1) · 1 6

. Аналогично, 4b + 1 6 2b + 1, 4c + 1 6 6 2c+1. Значит, √4a + 1+√4b + 1+√4c + 1 6 2a+1+2b+1+2c+1 =

= 2 · (a + b + c) + 3 = 5. Осталось показать, что равенство невозможно (доказать строгое неравенство). Действительно, неравенства

обратятся в равенство, если 4a+1 = 1, 4b+1 = 1, 4c+1 = 1. Тогда a = b = c = 0, что противоречит условию a + b + c = 1.

14. Обозначим: x = a + b, y = b + c, z = c + a. Тогда a + b + c =

. Пре-

образуя левую часть неравенства, получим

. Следует отметить, что данное неравенство обращается в равен-

ство лишь при a = b = c.

15. Домножим неравенство на 2 и перенесем все слагаемые в одну часть. Получим 2a²+ 2b²+ 2c²− 2ab − 2ac − 2bc = (a − b)²+ (b−c)²+(c−a)²> 0. Заметим, что левая часть равна 0, только если

a = b = c.

16. Раскладывая на множители, получим, a³+ b³+ c³− 3abc =

= a³+3a²b+3ab²+b³+c³−3ab(a+b+c) = (a+b)³+c³−3ab(a+b+c) = = (a + b + c)(a²+ b²+ c²− ab − ac − bc) = 0.

Учитывая неравенство из задачи 15 и то, что a ≠ b, получим

a + b + c = 0.

Тема 7. Системы счисления

Немногие знают, что при помощи загибания пальцев можно досчитать вовсе не до 10, а до

1023.

Задача 1. Существует ли система счисления, в которой одно-

временно

а) 3 + 4 = 10 и 3 · 4 = 15;

б) 2 + 3 = 5 и 2 · 3 = 11?

Задача 2. Как разложить по семи кошелькам 127 рублевых бумажек так, чтобы любую сумму от 1 до 127 рублей можно было

бы выдать, не открывая кошельков?

Задача 3. Миша загадал число не меньше 1 и не больше 1000. Васе разрешено задавать только такие вопросы, на которые Миша может ответить «да» или «нет» (Миша всегда говорит правду). Мо-

жет ли Вася за 10 вопросов определить загаданное число?

Задача 4. Имеется множество билетов с номерами от 1 до 30 (номера могут повторяться). Каждый из учеников вытянул один билет. Учитель может произвести следующую операцию: прочитать список из нескольких (возможно — одного) номеров и попросить их владельцев поднять руки. Сколько раз он должен проделать такую операцию, чтобы узнать номер каждого ученика? (Учеников не обя-

зательно 30.)

Задача 5. Один школьный учитель заявил, что у него в классе 100 детей, из них 24 мальчика и 32 девочки. Какой системой счис-

ления он пользовался?

Задача 6. Ваня, Веня, Вася и Валя ехали на троллейбусе. От нечего делать Ваня сидел у окна и считал троллейбусные столбы. Веня тоже считал столбы, но на другой стороне дороги.

— Ну и сколько вы насчитали? — спросил Вася, когда они вышли

на остановке.

— Я насчитал ровно 100, — ответил Ваня.

— И я насчитал ровно 100, — ответил Веня.

— Не может быть! — усомнился Валя, который увлекался городским транспортом. — У Вани должно быть на 13 столбов больше, я

гарантирую это!

— Может! — сказал Вася, увлекавшийся математикой. — Вы же

считаете в разных системах счисления!

Определите, в каких системах счисления считали Ваня и Веня,

если Валя считал в десятичной.

Задача 7. а) Кощей Бессмертный загадывает три двузначных числа: a, b и c. Иван Царевич должен назвать ему три числа x, y и z, после чего Кощей сообщит ему сумму ax+by +cz. Иван Царевич должен отгадать задуманные числа, иначе ему отрубят голову. Как

ему спастись?

б) Кощей Бессмертный загадывает три любых натуральных числа: a, b и c. Иван Царевич называет ему три числа x, y и z, после чего Кощей сообщает ему сумму ax+by+cz. Иван Царевич должен отгадать задуманные числа за два таких «хода», иначе ему отрубят

голову. Как ему спастись?

Задача 8. Докажите, что число делится на 7 тогда и только

тогда, когда сумма цифр в его восьмеричной записи делится на 7.

Задача 9. Какое наименьшее число гирь необходимо для того, чтобы иметь возможность взвесить любое число граммов от 1 до 100 на чашечных весах, если гири можно класть только а) на одну б) на обе чашки весов?

Решения

1.а) Да (7-ричная система счисления). б) Нет. Второе равенство

могло бы выполняться только в 5-ричной системе счисления.

2.127 бумажек надо разложить так: 1+2+4+8+16+32+64.

3.Первый способ. Так как 1 6 n 6 1000 < 2¹⁰, то в двоичной системе счисления число n содержит не более 10 цифр. За один вопрос можно узнать любую цифру (например, спросив, равна ли она 1). Второй способ. Вася сначала спросит, больше ли число, чем 500. Затем, больше ли 750 или меньше ли 250, в зависимости от ответа Миши на 1-й вопрос, и т.д. каждый раз расстояние от числа в старом

вопросе до числа в новом вопросе уменьшается в два раза.

4.Закодируем билеты двоичными числами от 00001 до 11110. На k-м этапе учитель включает в список все номера, k-й разряд которых равен единице (например, на 3-м этапе номера 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, 28, 29, 30). После пятого этапа учитель узнает двоичный код номеров у всех учеников. Четырёх этапов недостаточно даже для одного ученика: число его «возможных» номеров после каждого этапа (если учителю «не повезет») может сократиться не

более чем вдвое.

5.Пусть x — основание той системы счисления, о которой идет речь. Тогда слова учителя означают следующее: у него x²учеников, из них 2x+4 мальчика и 3x+2 девочки. Таким образом, 2x+4+x+ 2 = x², или x²−5x−6 = 0. Имеем, x²−6x+x−6 = (x+1)(x−6) = 0. Так как x = −1 не может быть основанием системы счисления, то x = 6. Итак, ответ учителя был дан в шестеричной системе; при этом у него было тридцать шесть учеников, из них шестнадцать

мальчиков и двадцать девочек.

6.Пусть Ваня считал в системе с основанием p, а Веня — в системе с основанием q. Тогда Ваня и Веня насчитали 100_p= p²и 100_q= q²столбов соответственно. Из слов Вали следует, что p²−q²= (p−q)(p+q) = 13, поэтому p−q = 1, p+q = 13. В самом деле, число 13 имеет только делители 1 и 13, а p−q < p+q при натуральных p и q. Следовательно, p = 7, q = 6.

7.а) Иван Царевич должен назвать числа 1, 100, 100². Числа a,

b, c — «цифры» ответа Кощея в 100-ичной записи.

б) Первым ходом Иван называет, например, три единицы — пусть Кощей в ответ сообщает число p. Тогда Иван действует аналогично пункту a), используя систему счисления с основанием p,

называет числа 1, p и p².

8.a_na_n−1 ...a₁a₀₈− (a_n+ a_n−1 + ... + a₁+ a₀) = a_n· (8ⁿ− 1) + +a_n−₁·(8ⁿ⁻¹−1)+...+a₁·(8−1). Во всех слагаемых есть множитель 8^k− 1, который обязательно делится на 7 (убедитесь в этом самостоятельно), поэтому сумма цифр дает тот же остаток от деления

на 7, что и само число.

9.а) Любое число можно записать в двоичной системе счисления. Поэтому для взвешивания любого числа граммов от 1 до 100 достаточно иметь семь гирь с весами: 1, 2, 4, 8, 16, 32, 64. Шестью гирями обойтись нельзя, так как с их помощью можно взвесить не более 2⁶− 1 различных весов (каждая гиря либо участвует, либо не участвует во взвешивании).

б) При решении этой задачи нам понадобится следующее интересное свойство троичной системы счисления: любое натуральное число можно представить в виде разности двух чисел, запись ко-

торых в троичной системе счисления содержит только 0 и 1.

Для доказательства нужно записать исходное число в троичной системе счисления и построить требуемые числа поразрядно справа налево (в разложении исходного числа по степеням тройки каждое слагаемое вида 2 · 3^kзаменяем на 3^k⁺¹− 3^k). При этом если у получившихся чисел в каких-то одноименных разрядах стоят единицы,

то их можно заменить нулями.

Теперь понятно, что достаточно иметь 5 гирь с весами 1, 3, 9, 27, 81 (подумайте, почему не нужна гиря весом 243 грамма).

Четырех же гирь явно недостаточно, так как с их помощью можно взвесить не более 3⁴−1 = 80 различных весов (каждая гиря либо на левой чашке весов, либо на правой, либо не участвует во взвеши-

вании).

ОГЛАВЛЕНИЕ

Предисловие ....................................................................................................... 3

Задачи и решения XXII осеннего турнира по математике

и информатике «Черноризец Храбр» .............................................................. 5 Инструкция для 2 класса .................................................................................... 5

Задачи для 2 класса ............................................................................................ 6

Ответы и краткие решения для 2ласса ............................................................. 9

Инструкция для 3 - 4 класса ............................................................................. 11

Задачи для 3 - 4 класса ..................................................................................... 12

Ответы и краткие решения для 3 - 4 класса ................................................... 16

Инструкция для 5 - 6 класса ............................................................................. 20

Задачи для 5 - 6 класса ..................................................................................... 21

Ответы и краткие решения для 5 – 6 класса ................................................... 25

Инструкция для 7 - 8 класса ............................................................................. 29

Задачи для 7 – 8 класса ................................................................................... 30 Ответы и краткие решения для 7 – 8 класса 35 ...................................................

Инструкция для 9 - 10 класса ........................................................................... 39

Задачи для 9 – 10 класса ................................................................................. 40

Ответы и краткие решения для 9-10 класса ................................................... 47

Инструкция для 11 - 12 класса ......................................................................... 52

Задачи для 11 - 12 класса ................................................................................. 53

Ответы и краткие решения для 11 – 12 класса ............................................... 59

Материалы для подготовки к турниру «Черноризец Храбр»

и другим математическим состязаниям и конкурсам ................................... 65

Тема 1. Текстовые задачи ................................................................................ 65

Тема 2. Числа .................................................................................................... 70

Тема 3. Принцип Дирихле ................................................................................ 78

Тема 4. Геометрия ............................................................................................. 84

Тема 5. Комбинаторика ................................................................................... 90

Тема 6. Неравенства ....................................................................................... 100

Тема 7. Системы счисления ............................................................................ 105

Лазаров Борислав

Михайлов Евгений Владимирович

Турнир по математике и информатике

ЧЕРНОРИЗЕЦ ХРАБР

ЗАДАЧИ, РЕШЕНИЯ,

МАТЕРИАЛЫ ДЛЯ ПОДГОТОВКИ

Учебно-методическая разработка

Издание осуществляется в авторской редакции

Подписано в печать 06.05.2015. Формат 60х84 1/16. Бумага офисная.

Печ. л. 7,0. Тираж 100 экз. Заказ №114.

Издательство «КИРА»

163061, г. Архангельск, ул. Поморская, 34, тел. 650-670.

Отпечатано с готового оригинал-макета

Типография «КИРА»

163061, г. Архангельск, ул. Поморская, 34, тел. 65-47-11. e-mail: [email protected]

Б. ЛАЗАРОВ Е.В. МИХАЙЛОВ

Турнир по математике и информатике Черноризец Храбр. Задачи, решения, материалы для подготовки. Б. Лазаров, Е. В. Михайлов

Б. Лазаров, Е.В. Михайлов

Архангельск Издательство «КИРА» 2015

Лазаров, Борислав. Л 17 «Черноризец

Предисловие Учредителем турнира «Черноризец

Решение школьной задачи является для ученика маленьким научным открытием

Задачи и решения XXII осеннего турнира по математике и информатике «Черноризец

А) 12 Б) 10 В) 8 Г) 6

В поезде 10 вагонов. Иво находится в пятом вагоне, если считать от начала поезда

Сколькими различными способами можно разрезать фигуру на три пря- моугольника?

Ответы и краткие решения для 2 класса 1

Сейчас возраст ребенка 49 − 41 − 3 − 3 = 2 , а тогда матери 21 + 2 = 23

Пишите разборчиво ЗАГЛАВНЫМИ ПЕЧАТНЫМИ буквами

Каждый лестничный пролет между соседними этажами жилого дома имеет 23 ступени

А) 78 Б) 83 В) 88

А) 212 Б) 414 В) 515

Если у г-на Иванова была только одна монета достоинства 1лв

Ответы и краткие решения для 3–4 класса 1

Ответ В. Вафля стоит 56−24 = 32 стотинки

Ответ В. Каждый присоединенный стол дает 2 дополнительных места

Перед этим у него было 10 + 20 = 30 долларов, что является удвоенной суммой, с которой он начал первую партию в казино, т

Инструкция для 5–6 класса 1.

А) 7,73 Б) 6,73 В) 6,83

Какое наименьшее число таких сто- • • • лов нужно соединить последователь- но, чтобы разместить 20 человек?

Д) на одной ветке 4 воробья, а на остальных по 3 1

В супермаркете пакуют поступившие яблоки в пакеты

Играя в казино в Лас-Вегасе, Джо всегда удваивает сумму денег, с которой начал игру

Значит, 2 n + 2 = 20 , а n = 9

Ответ Б. Перед каждым взвешивании монеты делятся на три группы: (671,671,671), (223,223,225), (75,75,73 или 75) и т

Следовательно, самый дальний дом с нечетным номером, до которого они могли дойти, это №199

Ответ Б. Пусть X такая сумма денег, которая не меняется после уменьшения на 20 и последующего удвоения

Пишите разборчиво ЗАГЛАВНЫМИ ПЕЧАТНЫМИ буквами

Сколько имеется трехзначных квадратных чисел? (Квадратное число — это количество точек в квадрате — в каждой строке и в каждом столбце имеется одинаковое количество точек

Сколько всего было участников?

Точки C и D лежат на отрезке

Точка I — внутренняя для треугольника со сторонами 3, 4 и 5см

Сколько было учеников в команде?

А) 0 Б) 1 В) 2 Г) 3

При z = 2 есть еще одно множество: {4 , 3 , 2}

Ответ В. Поскольку 2013 = 3 · 11 · 61 , имеем x + 2 y + y + +2 z + z +2 x…

Ответ В. При последовательном вычислении цифр после запятой получим, что 6-я и 7-я цифры 3

НОД ( m ;10 n ) = 1 , то m делит 11

Замечание. Рисунки не обязательно точны — они только отоб- ражают описываемую в условии конфигурацию

Общая сумма поездки оказалась равной 30 полным билетам

AB : BC : CD : DA = 1 : 2 : 4 : 3

В командном соревновании по математике каждый ученик одной команды участвовал в решении двух задач, каждая задача решалась четырьмя учениками, а для любой пары задач только…

Чему равен остаток от деления 2013 2013 на 13?

Д) ни одно из перечисленных 18

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

27.01.2020