Урок изучения нового материала по теме "Теорема Пифагора"

Цели урока:

·        Сформулировать и доказать одну из важнейших теорем геометрии – теорему Пифагора и показать ее применение при решении задач;

·        Развитие логического мышления, математической речи:

·        Воспитание устойчивого внимания, любознательности.

Оборудование:

·        Карточки- задания для индивидуальной работы;

·        Карточки-задания для групповой работы;

·        Презентация к уроку;

·        Компьютер;

·        Проектор.

Ход урока

I.                    Организационный момент

Сообщение темы и задач урока

Эпиграф:

«Геометрия владеет двумя сокровищами: одно их них – это теорема Пифагора»

                                Иоганн Кеплер

II.                 Подготовка к восприятию нового материала

1.     Индивидуальная работа

1)D        N                   C                 Задание:

                                                   Докажите, что PNKM - квадрат

                                 M

P

A                     K         B

2.     Групповая работа

1 группа:                                                  Задание:

                                                   Найдите площадь заштрихованной

                                                   фигуры

2 группа:

                                              В                                                              Задание:

                              С                               А                                 Найдите площадь четырехугольника                    

                                                                               ABCD

                                D

3.       Фронтальная работа

1)     Сторона квадрата равна 3 см. Найдите его площадь.

2)     Площадь квадрата равна 25 м². Найдите его сторону.

3)     Какой треугольник называется прямоугольным?

4)     Как называются стороны в прямоугольном треугольнике7

5)     Назовите катеты и гипотенузу в треугольниках, изображенных на рисунке

                                                              (треугольник не прямоугольный)

6)     Найдите площадь прямоугольного треугольника, если его катеты равны 3см и 4 см.

III.               Изучение нового материала

Задача-исследование

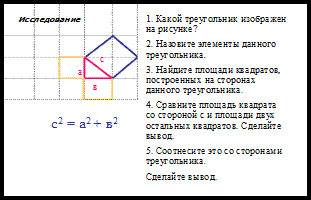
- Какую зависимость мы с вами получили ?

- Прочтите правильно полученную формулу (В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катета).

- Ребята  вот это утверждение в геометрии получило название теорема Пифагора.

- С чем мы сегодня с вами на уроке познакомимся? Какова цель нашего урока? Для чего изучается теорема Пифагора?

Историческая справка

Кто же такой Пифагор? Когда была открыта эта теорема и почему она так

называется?

                                                        -  Пифагор – древнегреческий ученый

                                                         - Родился он около 580 г до н.э.

                                                         - Занимался математикой, философией,

                                                            естественными науками

- Интересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений. Пифагор по-видимому нашел доказательство этого соотношения. Сохранилось древнее придание, что в честь своего открытия Пифагор принес в жертву богам быка, по другим свидетельствам  - даже сто быков.

- На протяжении последних веков были найдены различные другие доказательства теоремы Пифагора. В настоящее время их насчитывается более ста.

Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Pons asinorum – ослиный мост или eleguga – бегство убогих, так некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики заучивали теорему наизусть без понимания и прозванные поэтому «ослами» не были в состоянии преодолеть теорему Пифагора, служившую для них вроде непроходимого моста.

- Теорему Пифагора учащиеся так же называли «ветряной мельницей», составляли стишки вроде этого:

Пифагоровы штаны

    Во все стороны равны

И рисовали карикатуры:

- Предполагают, что во времена Пифагора теорема звучала по-другому: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».

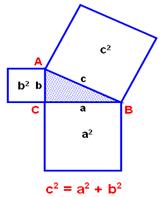
- Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников. Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. Из рисунка  видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.

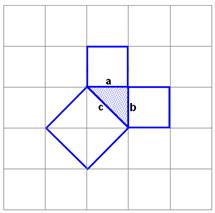 («Пифагоровы штаны во все стороны равны»)

- О теореме Пифагора

Пребудет вечной истина, как скоро

Все познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

            Обильно было жертвоприношенье

            Богам от Пифагора. Сто быков

            Он отдал на закланье и сожженье

            За света луч, пришедший с облаков.

Поэтому всегда с тех самых пор,

Чуть истина рождается на свет,

Быки ревут, ее почуя, вслед.

            Они не в силах свету помешать,

            А могут лишь закрыв глаза дрожать

            От страха, что вселил в них Пифагор.

А. Шамиссо

- А сейчас докажем теорему Пифагора в современной формулировке.

Т е о р е м а. «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».

                                                               Дано:      АВС - прямоугольный

    D                                  E                                АС= с -гипотенуза                   

                                         M                               АВ= b - катет

       A                                                                  ВС = а - катет

      B                                N                   Доказать: с² = а² + b²

Доказательство

1.     Достроим треугольник до квадрата со стороной (a + b)

2.     Sкв = (a + b)²

3.     Sкв = S_KACM + 4S   _ABC

Sкв = c² + 4 ∙  ab

Sкв = c² + 2ab

4.     (a + b)² = c² + 2ab

a² + 2ab + b² – c² – 2ab = 0

a² + b² – c² = 0

a² + b² = c²                             

                                ч.т.д.

IV.              Закрепление  нового материала

Задание 1. В прямоугольном треугольнике АВС, а, b – катеты, с – гипотенуза. Заполните таблицу.

                                                                                              Ответы: 

Задача 2.  № 487

Задача 3. № 493

V.                 Самостоятельная работа (разноуровневая)

Вариант 1. 

                                          х

            6                                                                    

                                       8          

               Вариант 2.

                                    10

               Х

                                      8                                   

                     Вариант 3.

                                   у                    

VI.              Итог урока

- Что ты узнал сегодня нового?

 -  Сформулируй теорему Пифагора.

 -  Что тебе понравилось?