Урок подготовки к ЕГЭ. Особенности решения задач по теме «Системы счисления»

Урок подготовки к ЕГЭ. Особенности решения задач по теме «Системы счисления» (в формате ЕГЭ по информатике и ИКТ)

Цель: познакомиться с методами решения задач по теме «Системы счисления» в формате ЕГЭ по информатике.

Вопросы занятия:

Какие задания по теме «Системы счисления» есть в ЕГЭ по информатике?

Каковы основные методы решения задач по данной теме?

Ход занятия:

 Разбор решения задач в формате ЕГЭ.

Задание:

 Решить задачу.

Сформулируйте алгоритм решения для задач каждого типа.

Решение:

Представим целую часть числа в двоичной системе счисления.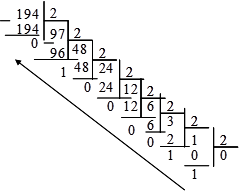

19410 = 11000010₂

Представим дробную часть числа в двоичной системе счисления.

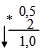
0,510=0,12

Таким образом, 194,510=11000010,12. В двоичной записи 4 единицы.

Ответ: 4

2.  В каком отношении находятся числа 10010012 и 1118?

1) их невозможно сравнить, потому что они записаны в разных

системах счисления;

2) первое число меньше второго;

3) первое число больше второго;

4) они равны.

     Решение: Чтобы сравнить числа, их необходимо представить в одной из предложенных в задании систем счисления, например, восьмеричной. Переведем число 10010012 в восьмеричную систему счисления. Для этого разобьем число на триады (группы по 3 цифры) справа налево и запишем вместо каждой группы соответствующую восьмеричную цифру.

10010012 ®1 001 0012 ® 1118.

Следовательно, 10010012 = 1118.

Ответ: 4

Обсуждение: Задание на сравнение чисел, представленных в различных системах счисления, базового уровня сложности. Есть и другие способы решения этой задачи. В частности, можно перевести оба числа в десятичную систему счисления и сравнить их:

10010012=1 ∙ 26+1 ∙ 23+1=7310,

111₈=1 * 8²+1 * 8¹+1 * 8⁰=7310.

3. Дано А = 2478, B = A916. Какое из чисел C, записанных в двоичной системе, отвечает условию A < C < B ?

1) С = 101010002 2) С = 101010102 3) С = 101010112 4) С = 101011002

Решение:

Для сравнения необходимо представить числа в одной системе счисления, в данном случае двоичной, т. к. варианты ответа – двоичные числа. Для этого каждую цифру восьмеричного числа заменим триадой (группой из 3 двоичных цифр): 2478®10 100 1112.

Аналогично переведем шестнадцатеричное число, заменяя цифры четверкой двоичных цифр: A916®1010 10012.

Далее приступаем к сравнению:

101001112 < 101010002 и 101010002 < 101010012 (A < C < B).

(Вообще говоря, на этом можно остановиться, т.к. решение найдено.)

101001112 < 101010102 и 101010102 > 101010012 (A < B < C).

101001112 < 101010112 и 101010112 > 101010012 (A < B < C).

101001112 < 101011002 и 101011002 > 101010012 (A < B < C).

Ответ: 1

Обсуждение: Задание на сравнение чисел, представленных в различных системах счисления, базового уровня сложности.  Возможен способ решения, при котором сначала все числа переводятся в десятичную систему счисления, а затем сравниваются: 2478 =2 ∙ 82+4 ∙ 8+7=16710, A916=10 ∙ 16+9=16910.

101010002=1 ∙ 27+1 ∙ 25+1 ∙ 23=16810 (A < C < B).

101010102=1 ∙ 27+1 ∙ 25+1 ∙ 23+1 ∙ 2=17010 (A < B < C).

101010112=1 ∙ 27+1 ∙ 25+1 ∙ 23+1 ∙ 2+1=17110 (A < B < C).

101011002=1 ∙ 27+1 ∙ 25+1 ∙ 23+1 ∙ 22=17210 (A < B < C).

 4. Чему равна сумма чисел 348 и 4616?

1) 1028 2) 1428 3) 17A16 4) 10100102

Решение:

Для вычисления суммы необходимо сначала представить числа в одной системе счисления. Выполнять сложение привычнее в десятичной системе счисления, однако для этого нужно выполнить больше действий (придется переводить в десятичную систему заданные числа и все 4 варианта ответа), следовательно, больше времени будет затрачено на решение задачи. Переведем числа в двоичную систему счисления и выполним сложение.

348®11 1002

4616®100 01102

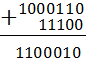
Дальнейшие действия сводятся к тому, чтобы представить полученный результат в системах счисления, указанных в вариантах ответа, и выбрать тот вариант, с которым совпадет полученное число.

Среди представленных вариантов ответа есть только одно число в двоичной системе счисления, но это число не совпадает с полученным результатом. Поэтому переведем значение суммы в 8-ричную систему.

11000102®1 100 0102®1428. Среди предложенных вариантов такой ответ есть, поэтому решение окончено.

Ответ: 2

Обсуждение: Задание на умение выполнять арифметические операции в двоичной, восьмеричной и шестнадцатеричной системах счисления базового уровня сложности. Дополнительную сложность представляет то, что все результаты представлены в разных системах счисления, и учащийся должен провести анализ задания и выбрать систему счисления для выполнения арифметических операций, так, чтобы сделать минимум расчетов и свести к минимуму количество арифметических ошибок.

Решение:

1 способ

Для вычисления разности данных чисел представим первое из них в двоичной системе счисления и выполним вычитание.

1018®1 000 0012

  1000001

    100111

      11010

Дальнейшие действия сводятся к тому, чтобы представить полученный результат в системах счисления, указанных в вариантах ответа, и выбрать тот вариант, с которым совпадет полученное число.

110102®11 0102®328

110102®1 10102®1А16

Среди предложенных вариантов такой ответ есть.

Ответ: 1

2 способ

Переведем второе число в восьмеричную систему счисления и найдем разность чисел.

1001112®100 1112®478,

Дальнейшие действия сводятся к тому, чтобы представить полученный результат в системах счисления, указанных в вариантах ответа, и выбрать тот вариант, с которым совпадет полученное число.

328®11 0102®1 10102®1А16. Среди предложенных вариантов такой ответ есть. 

Ответ: 1

 Обсуждение: Задание на умение выполнять арифметические операции в двоичной, восьмеричной и шестнадцатеричной системах счисления базового уровня сложности. Дополнительную сложность представляет то, что все результаты представлены в разных системах счисления, и учащийся должен провести анализ задания и выбрать систему счисления для выполнения арифметических операций, так, чтобы сделать минимум расчетов и свести к минимуму количество арифметических ошибок.

Чему равно х, если выполнено равенство 25х + 183х = 126х? Если таких значений х несколько, перечислите их через запятую в порядке

возрастания.

Решение:

Запишем числа в виде суммы разрядных слагаемых:

            25х=2 ∙ x1+5 ∙ x0,

            183х=1 ∙ (3x)1+8 ∙ (3x)0,

            126х=1 ∙ (6x)1+2 ∙ (6x)0,

Подставим полученные выражения в данное уравнение и решим его:

2 ∙ x1+5 ∙ x0+1 ∙ (3x)1+8 ∙ (3x)0 = 1 ∙ (6x)1+2 ∙ (6x)0,

5x+13 = 6x+2,

х = 11.

Ответ: 11.

7. Укажите основание системы счисления, в которой 16´16=304. Если таких оснований несколько, перечислите их через запятую в порядке

возрастания.

Решение:

Пусть х – основание системы счисления. Тогда справедливо равенство: 16х ∙ 16х=304х

Запишем числа в виде суммы разрядных слагаемых и подставим полученные выражения в уравнение:

            (1∙ х1+6∙ х0)(1∙ х1+6∙ х0)=(3∙ х2+0∙ х1+4∙ х0)

            (х+6)2=3x2+4

Раскрывая скобки, получаем квадратное уравнение и решаем его.

x2–6x–16=0 ó

Отрицательный корень не может быть использован как основание системы счисления.

Ответ: 8

Задачи для самостоятельного решения:

А3 Дано: а=D716, b=3318. Какое из чисел c, записанных в двоичной системе, отвечает условию a<c<b?

А4 Вычислите сумму чисел x и y, при x = A616, y = 758.

Результат представьте в двоичной системе счисления.

А4 Чему равна сумма чисел 438 и 5616?

А11 Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится

А11 Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов ГБАВ и записать результат шестнадцатеричным кодом, то получится:

В3 Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11.

В3 Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.

В3 В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.