СПРАВОЧНЫЕ МАТЕРИАЛЫ ПО ТЕМЕ
ВЕКТОРЫ.
МЕТОД КООРДИНАТ.
|
1. Координаты вектора
|
|
2. Сложение и вычитание векторов
|
|
3. Умножение вектора на число
|
|
4. Расстояние между двумя точками
Пример: А(4; 2) B(8; 6)
|
|
5. Длина вектора
Пример:
|
|
6. Скалярное произведение векторов
Пример: |
|
7. Скалярное произведение векторов в координатах
Пример:
|
|
8. Косинус угла между ненулевыми векторами
|
|
9. Координаты середины отрезка
Пример: C - середины отрезка, соединяющего
точки A(-2, 4) и B(-4, 10) |
Результат скалярного произведения векторов является числом
(в отличие от других действий с векторами — сложения, вычитания и умножения на число, таких случаях результатом был вектор). При умножении вектора на вектор получается число, так как длины векторов — это числа, косинус угла — число — соответственно, их произведение также будет являться числом.
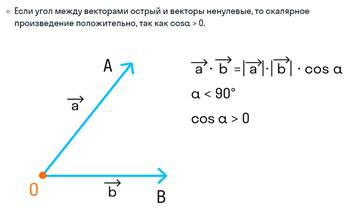
1. Если угол между векторами острый, то скалярное произведение будет положительным числом (так как косинус острого угла — положительное число).
2. Если векторы сонаправлены, то угол между ними будет равен 0° , а косинус равен 1 , скалярное произведение также будет положительным.
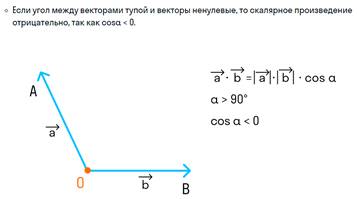
3. Если угол между векторами тупой, то скалярное произведение будет отрицательным (так как косинус тупого угла — отрицательное число).
4. Если векторы направлены противоположно, то угол между ними будет равен 180° . Скалярное произведение также отрицательно, так как косинус этого угла равен −1
. Справедливы и обратные утверждения:
1. Если скалярное произведение векторов — положительное число,
то угол между данными векторами острый.
2. Если скалярное произведение векторов — отрицательное число,
то угол между данными векторами тупой.
3. Особенный третий случай!
Обрати внимание!
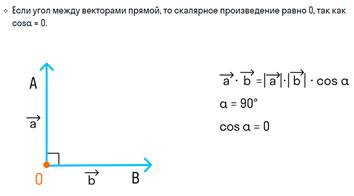
Если угол между векторами прямой, то скалярное произведение векторов равно нулю, так как косинус прямого угла равен 0 .
И обратно:
Если скалярное произведение векторов равно нулю, то эти векторы перпендикулярны
СПРАВОЧНЫЕ МАТЕРИАЛЫ ПО ТЕМЕ
Координаты вектора 2
Результат скалярного произведения векторов является числом (в отличие от других действий с векторами — сложения, вычитания и умножения на число, таких случаях результатом был вектор)
© ООО «Знанио»
С вами с 2009 года.
