Вычисление неопределенных интегралов

28.03.2023   преподаватель Шумская Л.А.

Практическое занятие 76

Тема. Вычисление неопределенных интегралов.

Цели: ознакомить студентов с неопределенным интегралом, сформировать навыки вычисления неопределенных интегралов методом непосредственного интегрирования и с помощью метода замены переменной; развивать логическое мышление и вычислительные навыки, навыки самостоятельной работы.

Студент должен знать:

·         понятие неопределенного интеграла;

·         свойства неопределенного интеграла;

·         таблицу неопределенных интегралов;

·         методы интегрирования: метод непосредственного интегрирования, замены переменной.

Должен уметь:

1.       вычислять неопределенные интегралы с помощью метода непосредственного интегрирования и замены переменной.

План.

1.      Неопределённый интеграл и его свойства

2.   Непосредственное интегрирование

3.      Метод замены переменной.

1.      Неопределённый интеграл и его свойства.

Определение. Множество всех первообразных для функции  называется неопределенным интегралом, обозначается  и читается как "интеграл эф от икс де икс"

Если функция  является одной из первообразных для , то по определению .

Здесь  - знак интеграла,  - подынтегральная функция,  - переменная интегрирования,  - постоянная интегрирования. За переменную интегрирования можно принять любую переменную. Нахождение функции по производной называется интегрированием. Интегрирование представляет собой операцию, обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.

Например:

 , где 

Проверка: 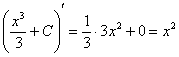 – исходная подынтегральная функция.

Любая ли функция интегрируема? Нет.

Сформулируем достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.

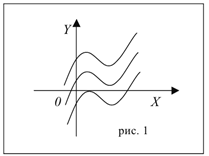
Геометрически выражение  можно изобразить как семейство кривых, полученных параллельным переносом любой из них вдоль оси OY (рис. 1).

Свойства неопределенного интеграла.

1.                      Производная от неопределенного интеграла равна подынтегральной функции, то есть если  = f(x), то 

2.                      Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

3.                       Неопределённый интеграл от алгебраической суммы  функций равен алгебраической сумме интегралов:

4.                      Постоянный множитель можно выносить за знак интеграла, то есть если a=const, то 

Таблица основных интегралов

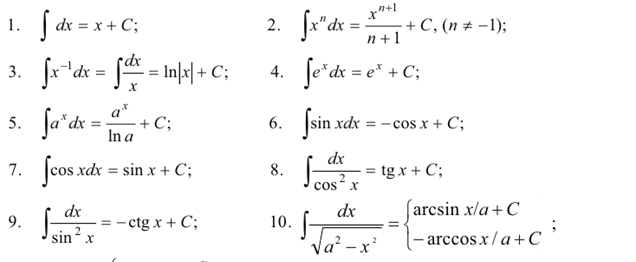
Интегралы, содержащиеся в этой таблице, принято называть табличными. Отметим частный случай формулы 1: 

Приведем еще одну очевидную формулу:  ,

т. е. первообразная от функции, тождественно равной нулю, есть постоянная.

2.      Непосредственное интегрирование

Под непосредственным интегрированием понимают такой способ нахождения интеграла, когда путём тождественных преобразований подынтегральных функций и использованием свойств неопределённого интеграла приходим к одному или нескольким табличным интегралам.

Пример 1 По определению найдите неопределенные интегралы.

Решение:

Так как:

Пример 2  Найдите интеграл .

Решение:

Производной какой функции является функция . Например, производной функции  является функция . Значит, множителем искомой функции является дробь , которая потом сократиться с коэффициентом 4 и получится . Такой функцией является функция . Значит, 

Пример 3  Найти интеграл 

Решение: Используем свойство степени с отрицательным показателем  и найдём неопределённый интеграл от степенной функции:

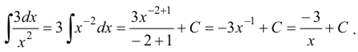
Пример 4 Найдите неопределенный интеграл 

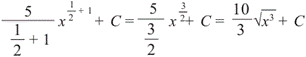
Пример 5. Найти неопределенный интеграл.

Пример 6. Найти интеграл 

Решение: Используем свойство степени с дробным показателем  и найдём неопределённый интеграл от степенной функции:

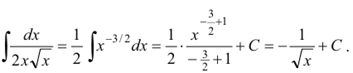
Ответ:

Пример 7  Найдите интеграл .

Решение:

Пример 8  Найти неопределенный интеграл.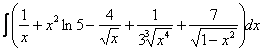

Решение:

Пример 9   Найти неопределенный интеграл.

Решение:

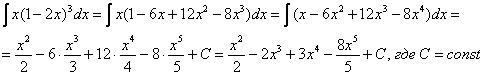
В данном примере мы использовали формулу сокращенного умножения

Пример 10   Найти неопределенный интеграл 

Решение:

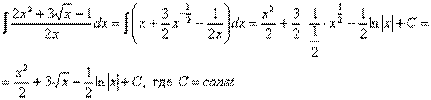
Замена переменных

Для упрощения подынтегральной функции и, тем самым, для нахождения интеграла часто применяется так называемая подстановка или замена переменных.

Если обозначить  и сделать соответствующие преобразования в заданном подынтегральном выражении, полученный интеграл при удачном выборе функции  может оказаться более простым или даже табличным.

Пример 11   Найти неопределенный интеграл.

для решения интеграла применим табличную формулу , и интеграл сведём к ней.

Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.В данном случае напрашивается: 

Итак: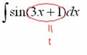 
Но при замене у нас остаётся ! Если осуществляется переход к новой переменной , то в новом интеграле всё должно быть выражено через букву ,  Следует вывод, что  нужно превратить в некоторое выражение, которое зависит только от .

Действие следующее. После того, как мы подобрали замену, в данном примере,  , нам нужно найти дифференциал . Так как , то 

В итоге: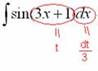  
Таким образом:  
А это уже табличный интеграл , справедлива и для переменной .

В заключении осталось провести обратную замену. Вспоминаем, что .

Чистовое оформление рассмотренного примера должно выглядеть примерно так:

Проведем замену:   

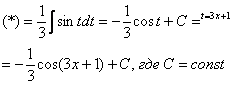
Значок  не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений.

Пример 12  Вычислить интеграл 

Решение:  Для вычисления этого интеграла сделаем простейшую подстановку:

В результате этой замены получим табличный интеграл:

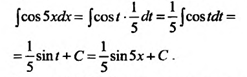
Пример 13  Найти неопределенный интеграл.

Проведем замену:      

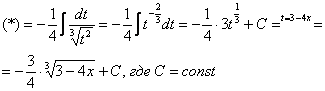
Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.

Пример 14  Найти неопределенный интеграл.

Замена:    
Время от времени в ходе решения интегралов встречается следующий трюк:  мы выразим из той же замены !

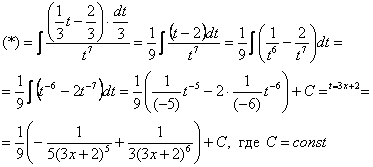
Пример 15   Вычислить интеграл: 

Решение:

Воспользуемся подстановкой и преобразуем, заданный интеграл, к табличному:

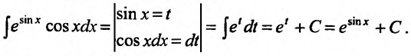
Домашнее задание:

1.      Составить опорный конспект и выучить определения.

2.       Выучить таблицу интегралов !!!

3.      Выполнить самостоятельную работу:

ВНИМАНИЕ! Выполненное домашнее задание в виде документа Word или фото   присылать  на  электронный  адрес dpec_matematika@mail.ru

Подпишите, пожалуйста, файл – Фамилия, имя, группа и дата занятия.

Например, Петров, МО-21, 11.02. Высылайте каждое задание отдельным файлом.

Скачано с www.znanio.ru