ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИИ ПО ФОРМУЛЕ 2урок

Вычисление значений функции по формуле

Цели: продолжить формировать умение находить значение функции по формуле, а также формировать умение находить значение аргумента, соответствующее заданному значению функцию, умение решать практические задачи с использованием функциональной терминологии.

Ход урока

I. Организационный момент

Устная работа.

1. Найдите значение функции у = 2х – 1 для значений аргумента, равного 0; 1; 2; –1.

2. Найдите область определения функции:

а) у = 3х – 7;         б) у = ; в) у = x³ – 2x² – 1; г) у = ;    

II. Формирование умений и навыков.

1. № 273, № 274.

2. Функция задана формулой у = 2х – 1.

а) Какое значение у соответствует х, равному 10; –4,5; 15; 251; 600?

б) При каком значении х соответствующее значение у равно: –19; –57; 205; –3?

Решение:

а) Если х = 10,                 то    у = 2 · 10 – 1 = 19;

    если х = –4,5,   то    у = 2 · (–4,5) – 1 = –10;

    если х = 15,                  то    у = 2 · 15 – 1 = 29;

    если х = 251,    то    у = 2 · 251 – 1 = 501;

    если х = 600,    то    у = 2 · 600 – 1 = 1199.

б) Если у = –19,   то    2х – 1 = –19;

                                                 2х = –19 + 1;

                                                 2х = –18;

                                                 х = –9; то есть у = –19, при х = –9.

    Если у = –57,   то    2х – 1 = –57;

                                                 2х = –57 + 1;

                                                 2х = –56;

                                                 х = – 28, то есть у = –57 при х = – 28.

    Если у = 205,   то    2х – 1 = 205;

                                                 2х = 205 + 1;

                                                 2х = 206;

                                                 х = 103, то есть у = 205 при х = 103.

    Если у = –3, то    2х – 1 = –3;

                                                 2х = –3,5 + 1;

                                                 2х = –2,5;

                                                 х = –1,25, то есть у = –3 при х = –1.

1. Из формулы равномерного движения s = υt выразить скорость υ как функцию пути s и времени t. Вычислить по этой формуле среднюю скорость полета пули, если s = 3 км, t = 6 с.

2. № 276.Решение:

Обозначим  за  т  массу  пробки  в  граммах,  а  за  V – объем  в  см³. Тогда зависимость массы куска пробки от объема можно выразить формулой т = 0,18 · V.

а) Если V = 240,  то    т = 0,18 · 240 = 43,2 (г);

б) если т = 64,8, то    0,18 · V = 64,18;

                                                V = 64,18 : 0,18;

                                                V = 360 (см³).

Ответ: а) 43,2 г; б) 360 см³.

3. № 278.Решение:

Анализ условия: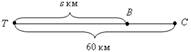

s = 12 · t.

а) Если t = 3,5,                 то   s = 12 · 3,5 = 42 (км);

б) если s = 30,                  то   12 · t = 30;

                                                t = 30 : 12;

                                                t = 2,5 (ч).

Ответ: а) 42 км; б) 2,5 ч.

4. № 352.Решение:

Анализ условия:

у = 1,5х + 150.

а) если х = 10,                 то   у = 1,5 · 10 + 150 = 15 + 150 = 165;

б) если у = 180,    то   1,5х + 150 = 180;

                                                1,5х = 180 – 150;

                                                1,5х = 30;

                                                х = 30 : 1,5;

                                                х = 20, значит, у = 180 при х = 20.

Ответ: а) у = 165; б) х = 20.

III. Проверочная работа.

Вариант 1

1. Функция задана формулой у = 3х – 7. Найдите значение аргумента, при котором значение функции равно нулю.

2. Найдите значение аргумента, при котором функция у = –3х – 2 принимает значение 0,3.

3. Запишите  область  определения  функции,  заданной  формулой
у = .

Вариант 2

1. Функция задана формулой у = 5 + 2х. Найдите значение аргумента, при котором значение функции равно нулю.

2. Найдите значение аргумента, при котором функция у = –5х + 11 принимает значение 0,2.

3. Запишите  область  определения  функции,  заданной  формулой
у = .

IV. Итоги урока.

– Дайте определение функции. Что называется аргументом, значением функции?

– Объясните на примере функции, заданной формулой у = 3х + 18

Домашнее задание: № 275; № 277; № 279; № 353.