ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИИ ПО ФОРМУЛЕ 3 урок

Вычисление значений функции по формуле

Цели: продолжить работу по усвоению понятия функции и связанных с функцией понятий (область определения функции, область значений функции и др.); формировать умение находить значения функций, заданных аналитически (с помощью формулы).

Ход урока

I.Организационный момент

 Устная работа.

1. Задайте формулой функцию, сопоставляющую каждому числу третью степень этого числа; сумму этого числа с числом 5.

2. Велосипедист едет со скоростью 15 км/ч и за t ч проходит расстояние s км (зависимость s от t). Найдите значение функции, соответствующее значению аргумента, равному ; 2; 2.

II. Объяснение нового материала.

Цель этого и последующих занятий – в упорядочении имеющихся представлений о функции, развертывании системы понятий, характерных для функциональной линии. Значительное место должно быть отведено усвоению важного представления – однозначности соответствия аргумента и определенного по нему значения функции. Для рассмотрения этого вопроса привлекаются различные способы задания функции.

Чаще других в математике и её приложениях применяется задание функции формулой. Все другие способы играют подчиненную роль. Однако сопоставление разных способов задания выполняет важную роль:

1) и  таблицы,  и  графики  служат  для  удобного  в  определенных обстоятельствах представления функции, имеющей аналитическую форму записи;

2) необходимо для усвоения всего многообразия аспектов понятия функции.

Объяснение проводить согласно пункту 13 учебника. Разбираем пример  № 1  со  с. 55  учебника.  Показываем,  что  для  того,  чтобы  найти значение функции, необходимо подставить некоторое значение аргумента в формулу.

Также объясняем, что в случае, когда область определения функции явно не задана, считают, что она состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

III. Формирование умений и навыков.

1. № 267.   2. Вычислить  значение  следующих  функций  при  х,  равном  –2; –1; 0; 1; 2.

а) у = 3х;               б) у = –2х;                  в) у = –х – 3;      г) у = 20х + 4.

2-я группа.

1. № 270.     2. № 271.Решение:

у = х (х – 3,5)

1. Найдите область определения функции, заданной формулой:

а) у = 3х + 2;                    б) у = ;             в) у = x⁷ + 2x – 3;

г) у = ;                      д) у = ;               е) у = .

2. № 351.Решение:

а) у = .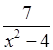

Область  определения  функции  –  все  числа,  кроме  тех,  при  которых х – 4 = 0, то есть х² = 4. Значит, не входят в ООФ х = 2 и х = –2.

б) у = .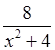

Область  определения  функции  –  все  числа,  кроме  тех,  при  которых х² + 4 = 0, то есть х² = –4.  Уравнение  не  имеет  решения,  значит, ООФ – любое число.

Ответ: а) любое число, кроме 2 и –2; б) любое число.

3. Дополнительные задания (для сильных учащихся).

3.1. Найдите область определения функции.

а) у =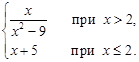

б) у =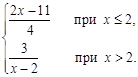

3.2. Задайте формулой какую-нибудь функцию, область определения которой:

а) все действительные числа;

б) все действительные числа, кроме –11;

в) все действительные числа, кроме 3 и 5;

г) все неотрицательные действительные числа;

д) все неположительные действительные числа.;

е) только одно число.

IV. Проверочная работа.

Вариант 1

1. Дана  функция  у = 2х² – 4х.  Найдите  значение  функции  при  х = 0
и х = –1.

2. Найдите область определения функции.

а) у = 2х – 7;                                б) у = ;

Вариант 2

1. Дана  функция  у = 5х² + х.  Найдите  значение  функции  при  х = 0
и х = 1.

2. Найдите область определения функции.

а) у = 3х + 6;                                б) у = ;

V. Итоги урока.

Домашнее задание: 1. № 268; № 269; № 272.