« Скрытые» проблемы в построении графиков линейных функций и их коррекция»

 

« Скрытые» проблемы в построении графиков линейных функций и их коррекция».

Цели урока:

-закрепить и обобщить знания учащихся, полученных при изучении темы, отработать навыки построения графика линейной функции, выявить «скрытые» проблемы и затруднения для их дальнейшей коррекции ;

-способствовать развитию мышления и элементов творческой деятельности (интуиции, смекалки, умений сравнивать, анализировать, выявлять закономерности, обобщать, конкретизировать, классифицировать), сознательного восприятия учебного материала, интереса к предмету, формированию правильной и аргументированной математической речи;

-воспитывать ответственное отношение к учебному труду, уважительное отношение к сверстникам.

Оборудование: компьютеры, проектор, экран

Место проведения: компьютерный класс

Ход урока

1. Организационный момент

2. Проверка домашнего задания

1) фронтальный опрос:

-сформулируйте определение линейной функции;

-что является графиком линейной функции? Как построить график линейной функции?

-как расположен в координатной плоскости график функции y=kx при k >0 и при k <0?

-в каком случае графики двух линейных функций пересекаются? Как найти координаты точки пересечения?

-в каком случае графики двух линейных функций являются параллельными прямыми?

2) парный взаимоконтроль (к проверке домашней работы подключены наиболее подготовленные ученики), № 318, № 320;

3. Закрепление пройденного материала

Каждый ученик индивидуально работает за компьютером, ответ записывает в лист учёта знаний (под копирку). После выполнения работы проводится самопроверка (по готовым решениям на мониторе компьютера) и разбор ошибок.

На мониторе компьютера рисунки:

 

1) б) в)

у

у

а) б)

х

х

0

0

в)

х

д)

г

у

у

)

д)

х

 

 

 

 

 

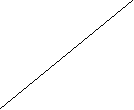
-График какой функции лишний? Почему?

-На каком рисунке изображён график прямой пропорциональности? Почему?

-На каком рисунке у графика линейной функции отрицательный угловой коэффициент?

 

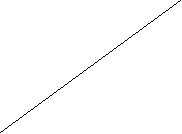
2) Какие графики нужно переставить, чтобы последовательность изучения функций не нарушалась?

у = -3х

у = 0,5х +1

а

у = 3х

) б) в)

 

 

 

 

3) Ученик допустил ошибку при построении графика одной из функций. На каком рисунке эта ошибка?

а) б) в)

у = 1/3х + 2

у = 1,5х

у = -х +1

 

 

 

4) На рисунки изображены графики следующих функций:

у = 3х, у = -3х, у = х-3. Под каким номером изображен график функции у = -3х?

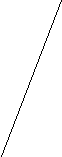
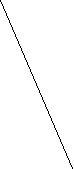1 2

3

 

 

 

 

5) Дана функция у = 2х – 5. Какой из приведённых ниже графиков является графиком этой функции?

а) б) в) г)

 

 

 

 

6) Дан график функции у = ах + b. Подберите формулу, задающую эту функцию.

а) у = 3х + 1; б) у = 1/3х + 1; в) у = -1/3х + 1; г) у = -3х + 1.

 

 

 

 

 

7) В одной системе координат построены графики функций у = 0,5х и у = -2. Определите по графику координаты точки их пересечения и запишите сумму этих координат.

 

 

а) -2,5 б)-1,5 в) -5 г) -6

8) Какие точки принадлежат графику линейной функции у = -0,5х + 1;

а) А(-1; 0); б) В(-2; 2,5); в) С(-2; 0); г) D(0; 1).

9) При каком значении х значение функции у = -0,5х + 1 равно 5:

а) х = 8; б) х = -8; в) х = -9.

10) Назовите функции, графики которых параллельны.

а) у = -2х – 1; у = -2х – 3,5; у = -2х + 5.

б) у = -0,5х; у = 0,5х – 3; у = 1,5х + 5.

в) у = -1/3х – 4; у = 1/3х – 4; у = 3х – 4.

11) Задайте формулой линейную функцию, график которой параллелен прямой у = -8х + 11 и проходит через начало координат.

Дополнительное задание:

Самостоятельная работа (задания дифференцированы).

1-й уровень

а) постройте в одной системе координат графики функций и укажите координаты точки их пересечения:

у = 0,5х+1 и у = -х+4.

Вычислите координаты точек пересечения графиков с осями.

б) укажите координаты точки пересечения графиков функций

у = - 0,5х+2 и у = -3+2х.

1.(-2;-1); 2.(-2;1); 3.(2;1); 4.(2;-1). 
2-й уровень

а) постройте график функции у = 1/2 (8 – х), где х >0;

б) задайте формулой линейную функцию, если известны угловой коэффициент kсоответствующей прямой и координаты точки А, через которую она проходит:

k = 2/3, А (-6;-3). Вычислите координаты точек пересечения графиков с осями.

Задайте формулой линейную функцию, график которой параллелен указанной прямой.

Самостоятельная работа сдаётся на проверку.

4. Подведение итогов урока

Даётся оценка работы класса.

5. Домашнее задание: №