И.В.Яковлев       |       Материалы по математике      |       MathUs.ru

Формулы приведения

Прежде чем обсуждать формулы приведения, давайте договоримся о терминологии. Пусть f(x) есть одна из функций: sinx, cosx, tgx или ctgx. Символом cof(x) обозначим кофункцию для функции f(x). Кофункциями друг для друга являются синус и косинус, а также, соответственно, тангенс и котангенс. Более точно:

•     если f(x) = sinx, то cof(x) = cosx;

•     если f(x) = cosx, то cof(x) = sinx;

•     если f(x) = tgx, то cof(x) = ctgx;

•     если f(x) = ctgx, то cof(x) = tgx.

Пусть n — ненулевое целое число. Формулы приведения — это тригонометрические тождества следующего вида:

если n чётное;

                                                                     2                     (±)cof(x),      если n нечётное;

Символ (±) перед функцией или кофункцией означает, что в том или ином случае там может стоять как плюс, так и минус.

Точку тригонометрической окружности, отвечающую углу nπ/2, мы будем называть опорной точкой.

Для каждой опорной точки (то есть при каждом n) получаются восемь формул приведения (четыре функции и два возможных знака перед α). Рассмотрим их в четырёх наиболее важных случаях — при n = 1,2,3,4.

1. Формулы приведения c опорной точкой π/2 (случай n = 1):

                                                                                              ;                                                            (1)

                                                                                              ;                                                            (2)

                                                                                                ;                                                            (3)

                                                                                              ;                                                             (4)

                                                                                              ;                                                            (5)

                                                                                              ;                                                        (6)

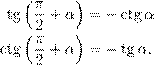                                                                                                                                                 ;                                                        (7)

(8)

Тождества для синуса и косинуса являются простым следствием формул сложения. Так, формулы дополнительного угла (1) и (2) уже были получены нами в предыдущей статье. Докажем формулу (5):

Аналогично доказывается и формула (6).

Тождества для тангенса и котангенса являются следствиями соответствующих тождеств для синуса и косинуса. Например, формула (3) получается в результате деления равенства (1) на равенство (2).

2.    Формулы приведения c опорной точкой π (случай n = 2):

sin(π − α) = sinα;	(9)
cos(π − α) = −cosα;	(10)
tg(π − α) = −tgα;	(11)
ctg(π − α) = −ctgα;	(12)
sin(π + α) = −sinα;	(13)
cos(π + α) = −cosα;	(14)
tg(π + α) = tgα;	(15)
ctg(π + α) = ctgα.	(16)

Формулы (15) и (16) показывают, что период тангенса и котангенса равен π. Этот факт уже известен нам из геометрической интерпретации тангенса и котангенса.

3.    Формулы приведения c опорной точкой 3π/2 (случай n = 3):

                                                                                            ;                                                    (17)

                                                                                            ;                                                     (18)

                                                                                              ;                                                        (19)

                                                                                            ;                                                          (20)

                                                                                            ;                                                    (21)

;           (22) ; (23)

                                                                                                                                                  (24)

4. Формулы приведения c опорной точкой 2π (случай n = 4):
sin(2π − α) = −sinα;	(25)
cos(2π − α) = cosα;	(26)
tg(2π − α) = −tgα;	(27)
ctg(2π − α) = −ctgα;	(28)
sin(2π + α) = sinα;	(29)
cos(2π + α) = cosα;	(30)
tg(2π + α) = tgα;	(31)
ctg(2π + α) = ctgα.	(32)

Формулы (29) и (30) отражают тот факт, что период синуса и косинуса равен 2π. Формулы (31) и (32) вытекают также из периодичности тангенса и котангенса с периодом π.

Любую формулу приведения можно вывести из формул сложения. Однако существует простое правило, позволяющее быстро получить нужную формулу. Оно состоит из двух шагов.

i.       Прежде всего задаём себе вопрос: «Меняется ли функция на кофункцию?» и двигаем туда-сюда головой вдоль той оси, на которой расположена опорная точка.

В случае опорных точек π/2 и 3π/2 это вертикальная ось ординат, и в результате получается утвердительный кивок: «Да, меняется». Мы видим это на примере формул (1)–(8) и (17)–(24): везде функция меняется на кофункцию.

В случае опорных точек π и 2π это горизонтальная ось абсцисс, и движение головой даёт отрицательный ответ: «Нет, не меняется». Мы видим это на примере формул (9)–(16) и (25)–(32): функция в правой части равенства везде та же, что и в левой.

ii.     Теперь нужно разобраться со знаком правой части. Когда ставится плюс и когда — минус?

Всё очень просто. Берём левую часть формулы приведения и предполагаем, что угол α острый, то есть точка α расположена в первой четверти. Определяем, в какой четверти расположен аргумент функции f и какой знак будет иметь функция f в данной четверти. Это и будет искомый знак правой части!

Так, точка π/2 − α будет также расположена в первой четверти, где все функции положительны. Соответственно, в правых частях формул (1)–(4) стоит знак плюс.

Точка π/2 + α окажется во второй четверти, где синус положителен, а косинус, тангенс и котангенс отрицательны. Соответственно, в правой части формулы (5) стоит знак плюс, а в формулах (6)–(8) — минус.

Точка π − α расположена во второй четверти. Поэтому в формуле (9) мы видим плюс, а в формулах (10)–(12) — минус.

Точка π+α расположена в третьей четверти, где синус и косинус отрицательны, а тангенс и котангенс положительны. Соответственно, в формулах (13), (14) мы видим плюс, а в формулах (15), (16) — минус.

Продолжая рассуждать так же, вы легко разберётесь со знаками и в оставшихся формулах приведения.

Таким образом, зубрить формулы приведения нет никакой необходимости. Никто их наизусть и не помнит :-) Если вы усвоили несложное правило «мотания головой» и определения знака правой части, то любую формулу приведения восстановите с лёгкостью. Ну а в самом крайнем случае вам на помощь придут формулы сложения — их, конечно, надо знать назубок.

Задачи

1.    Упростите выражение:

                                  а) );                          б)  ;

                                   в) ;                              г) .

2.    Упростите выражение:

а) sin(90^◦ − α) + cos(180^◦ + α) + tg(270^◦ + α) + ctg(360^◦ + α);

б)  .

3.    Упростите выражение:

                           а)  ;                          б)  ;                        в)  ;

                            г) cos(α − π);                              д) sin(α − π);                            е) tg(α − π);

                            ж) ;                       з) ;                      и)  .

4.    Пусть α, β и γ — углы треугольника. Докажите, что

.

5.    Синусы двух острых углов треугольника равны 3/5 и 5/13. Найдите косинус третьего угла треугольника.

6.    Косинусы двух углов треугольника равны 1/3 и 2/3. Найдите синус третьего угла треугольника.

7.    Упростите выражение:

                           а)  ;                     б)  ;

                           в)  ;                     г)

                           д)  ;                      е)  .

8.    Упростите выражение:

        а) sin²(180^◦ − α) + sin²(270^◦ − α);       б) );

         в) ;              г) .

9.    Вычислите:

а) cos20^◦ + cos40^◦ + cos60^◦ + cos80^◦ + cos100^◦ + cos120^◦ + cos140^◦ + cos160^◦;

б) cos1^◦ + cos2^◦ + cos3^◦ + ... + cos179^◦.