12. Методические рекомендации к проведению урока. Вариант 1

Методические рекомендации к проведению урока

Цель обучения: 6.5.1.6 решать текстовые задачи с помощью составления линейных уравнений;

Критерии оценивания:

-понимает условие текста задачи;

-по условию задачи вводит новую переменную;

-правильно составляет уравнение;

-правильно вычисляет;

-правильно определяет решение.

Организационный момент. Актуализацию опорных знаний проведите с помощью метода «Мозговой штурм». Объедините учащихся в однородные группы по 2 - 3 ученика, согласно выбранному уровню. Задание у всех групп одинаковое, но совместная работа с одноклассниками одного уровня позволит раскрыться каждому ученику.

Каждой группе раздайте рисунок с задачами, учащиеся должный составить  линейное уравнение и решить его.

Задание 1. Определите, при каком значении x равны значения выражений:

Решение:

Задание 2. На левой чаше весов, изображенных на рисунке, находится пачки чая и гиря массой 50 г, а на правой чаше – 1 пачка чая  и гиря массой 500 г. Составьте по рисунку линейное уравнение, где масса одной пачки чая равна x гр.  Решите уравнение и  найдите массу  одной пачки чая.

Решение:

=150

Задание 3. В трехзначном числе зачеркнули последнюю цифру, и оно уменьшилось на 405. Какое число получилось?

Ответ: 45

Проведите формативное оценивание по критериям.

        Объедините учащихся в однородные группы по 2 - 3 ученика, согласно выбранному уровню. Задание у всех групп одинаковое, но совместная работа с одноклассниками одного уровня позволит раскрыться каждому ученику. Предложите ученикам выбрать уровень сложности задания по закреплению теоретического материала на более высоком уровне.

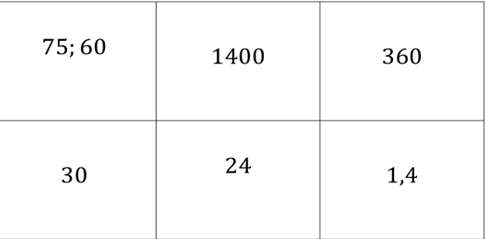
Самостоятельная работа – «Соберите пазлы».

Дидактическая цель: проверка и коррекция знаний учащихся по изученной теме, развитие познавательной компетентности учащихся.

Содержание игры. Раздайте группам задания, написаны вразброс на отдельном листе и комплект фигур с ответами. Решив задачу, группа находит фигуру с ответом и с помощью двойного скотча крепит ее на лист. Затем группа переходит к следующему заданию и снова находит фигуру с ответом и с помощью двойного скотча крепит ее на лист. Таким образом, решив все задания правильно, группа получит яркую картинку. Проверьте правильность выполненного задания, увидев все пазлы на нужных местах.

Выводы: игра направлена, прежде всего, на развитие познавательной компетентности учащихся; во время игры у детей вырабатывается привычка сосредоточиться, мыслить самостоятельно, развивается внимание, стремление к знаниям; увлекшись, дети не замечают, что учатся: познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию.

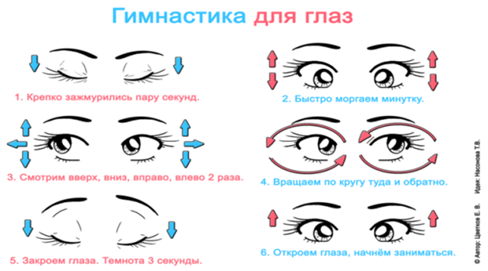
Проведите гимнастику для глаз.

Самостоятельная работа на проверку усвоения цели обучения. На данном этапе у учащихся развивается такая ценность академическая честность

После выполнения заданий, учащиеся проводят взаимопроверку правильности выполнения заданий по образцу, выданному учителем.

1. Составь уравнения и реши их, если:

а) значения выражений (Зр -12) и ( р +1) равны;

б) значения выражений (5а + 14) и (2а +7) являются противоположными числами;

в) значение выражения (1 - к) на 1 больше значения выражения (3 - 5х);

г) значение выражения (5 – у) в 3 раза больше значе­ния у.

Решение:

а) Зр -12 = р +1

3р – р = 1 + 12

2р = 13

Р = 6,5

Ответ: 6,5.

б) 5а + 14 + 2а +7 = 0

7а = - 21

а = -3.

Ответ: - 3.

в) 1 – к = 3 - 5х + 1

- к + 5к = 4 – 1

4к = 3

к = 3/4

Ответ: 3/4.

г) 5 – у = 3*у

-у - 3у = - 5

-4у = -5

У = 1,25

Ответ: 1,25.

2.В первой корзине было в 5 раз больше яблок, чем во второй. После того как из первой корзины взяли 8 кг яблок и переложили их во вторую корзину, яблок в корзинах стало поровну. Сколько яблок было перво­начально в каждой корзине?

Указания:

а) обозначь через х число яблок, находящихся первоначально во второй корзине;

б) заполни следующую таблицу:

в) составь уравнение;

г) реши уравнение;

д) дай ответ на вопрос задачи.

Решение:

x - было яблок во второй корзине
5х-было в первой корзине

5х-8=х+8
5х-х=8+8
4х=16
х=16:4
х=4 кг было во второй корзине
54=20 кг было в первой корзине

3. Используя указания к предыдущей задаче, реши сле­дующую:

В двух корзинах было поровну яблок. Если из пер­вой корзины взять 2,8 кг яблок, то во второй будет в 2 раза больше яблок, чем в первой. Сколько ки­лограммов яблок было в каждой корзине первона­чально?

Решение:

х кг было изначально

(х -2.8) стало в 1 корзине

2(х-2.8) = х

x =5.6 кг было

4.Туристы шли по дороге со скоростью 4 км/ч, а по шоссе - со скоростью 6 км/ч. На путь по шоссе они за­тратили на 3 часа меньше, чем на путь по дороге. Сколько времени туристы шли по шоссе, если пути по дороге и по шоссе равны? Используй при решении таблицу.

Учащиеся отвечают на вопросы рефлексии:

-        Что сегодня я узнал?

-        Мне было тяжело или нет?

-        Я понял материал или были затруднения?

-        Я научился чему-то новому?

-        Я смог добиться результата?

Ресурсы:

1.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

2.      Алдамуратова Математика. 6 класс. Алматы. «Атамура». 2011 год.

3.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

4.       Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.