13. Методические рекомендации к проведению урока. Вариант 1

Методические рекомендации к проведению урока

Цель обучения: 6.5.1.6 решать текстовые задачи с помощью составления линейных уравнений;

Критерии оценивания:

-понимает условие текста задачи;

-по условию задачи вводит новую переменную;

-правильно составляет уравнение;

-правильно вычисляет;

-правильно определяет решение.

Организационный момент. Приветствие. Отметка отсутствующих. Проверка готовности учащихся к уроку.Совместно с учащимися определяем цели урока и ожидаемые результаты. Учитель выполняет с учащимися упражнение на воспитание уверенности в себе и самоуважению.

«Дружеская мойка»

Учитель расставляет детей на небольшом расстоянии в два параллельных ряда лицом друг к другу. Один ученик проходит между этими рядами («через мойку»). Каждый дружески похлопывает его по спине или пожимает руку, одновременно произнося слова похвалы, симпатии и поощрения. В результате такой «мойки» появляется сияющий, радостный и счастливый ученик. Затем он встаёт в свой ряд, и процедура повторяется. (2-3 раза)

Разбор домашнего задания.

Учащиеся обмениваются домашним заданием и выполняют проверку по готовым решениям

Актуализация опорных знаний.

Предложите учащимся повторить пройденный материал с помощью метода «Правда или ложь?»

Цель метода: анализ суждении на основе имеющихся знаний, систематизация знаний, формативное оценивание. Предоставьте учащимся листочки с утверждениями (истинные и ложные). Учащиеся должны проставить число 1-если правда, 0-ложь.

1.      Проведите оценивание, за каждый правильный ответ – фишку или смайлик. Уравнение-это равенство, содержащие букву, значение которой надо найти;1

2.      Решить уравнение- значит найти все его корни (или убедиться, что корней нет);1

3.      Корень уравнения 0∙х=2, равен 0; 0

4.      Если перед скобками стоит знак «-», то нужно раскрыть скобки, сохранив знаки слагаемых;0

5.      120 больше 60 на 2; 0

6.       Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак;1

7.       Чтобы сложить подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть; 1

8.      Может ли сумма двух целых положительных чисел быть равной 0?0

9.      Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и тоже число, не равное нулю. 1

Предложите учащимся фронтальная работа. Ученики выполняют задания в парах, обучают друг друга, работают в «зоне ближайшего развития». Учитель оказывает поддержку ученикам по мере необходимости. Ценность: умение работать в сотрудничестве.

Задание №1. Решите уравнения:

;(y=-4)

; (n=0)

 ; (a=7)

;(c=2)

;(x=-24)

; (d=-9)

; (любой y)

(a=11)

Проверяем результаты, какие получили ответы?

Установление правильности и осознанности изучения темы

Работа в парах по рядам.

Задание №2. Придумайте задачу по уравнению:

1 пара: x + 3x = 16,

2 пара: x + (x +2) = 12, 

3 пара: 3x + 5x = 160

Учащиеся придумывают задачи и обмениваются с другой парой, затем проводят самооценивание и взаимооценивание.

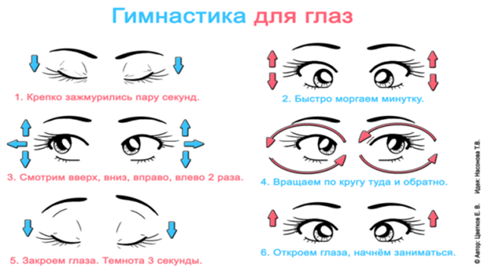
Проведите гимнастику для глаз.

    Предложите учащимся «Сундучок заданий». Составьте карточки с заданиями, сложите их в сундучок (контейнер). Учащиеся по очереди вынимают карточку из сундучка и выполняют задания. Остальные осуществляют проверку.

Дифференциация выражена в виде заданий, требующих разного уровня математической подготовленности, а так же с учетом скорости мышления и возрастных особенностей учащихся.

После выполнения заданий, учащиеся проводят взаимопроверку правильности выполнения заданий по образцу, выданному учителем.

А1. В питомнике было 450 саженцев яблонь и 180 саженцев слив. За день продали в 4 раза больше яблонь, чем слив, и саженцев осталось на 150 меньше, чем яблонь. Сколько всего саженцев продали за этот день?

Решение:

1)

2)

А2. В первом бассейне было в з раза больше воды, чем во втором. Когда из обоих бассейнов выкачали по 200м³ воды, во втором бассейне осталось в 5 раз меньше воды, чем в первом. Сколько кубических метров воды было в каждом бассейне первоначально?

Решение:

В первом бассейне:

В1.Из двух пунктов реки на встречу друг другу движутся две моторные лодки, собственные скорости которых равны. До встречи лодка, идущая по течению, прошла1 ,1 ч., а лодка, идущая против течения, 1,5 часа. Найдите собственную скорость лодок, если лодка, идущая по течению по течению до встречи прошла на 1 км больше другой лодки. Скорость течения реки 3 км /ч.

[1,1(х+3) – 1,5(х-3) =1]

В2.Из двух пунктов рек, расстояние между которыми 51 км , на встречу друг другу движутся две моторные лодки , собственные скорости которых равны . Скорость течения реки 3 км/ч.  Лодка, идущая по течению, до встречи прошла 1,5, а лодка, идущая против течения, 2 ч. Найдите собственную скорость лодок.

[1,5(х+3) + 2(х-3) = 51]

В3.Из Москвы в Ростов – на – Дону вышел пассажирский поезд со скоростью 60 км/ч. Спустя 2 ч. 10 мин из Ростова- на- Дону в Москву вышел пассажирский поезд со скоростью 80 км/x. На каком расстоянии от Москвы поезда встретятся, если расстояние между городами считать равным 1250 к?

[ 60х +80(х-) =1250]

.

В4. Лодка, двигаясь по течению реки, за 3 часа преодолевает такое же расстояние, как за 5 часов против течения реки. Найти скорость лодки, если скорость течения реки равна 3 км/ч.

Решение:

Пусть х - скорость лодки.  Скорость по течению х+3 км/ч, а против течения х-3 км/ч.

Путь по течению 3*(х+3), а против течения 5*(х-3).   (Время движения умножаем на скорость).

Т.к. пути равны, то приравниваем: 3(х+3) = 5(х-3)

3х + 9 = 5х - 15

2х = 24

х=12 - скорость лодки 

C1. Из пункта A в пункт B отправились три машины друг за другом с интервалом в 1 ч. Скорость первой машины равна 50 км/ч, а второй — 60 км/ч. Найти скорость третьей машины, если известно, что она догнала первые две машины одновременно.
Решение: Пусть на отрезке AB отмечена точка С. Точка А - точка отправления, точка В - точка назначения, точка С - место, в котором третья машина догнала и первую, и вторую машины.

Обозначим за t ч время, за которое первая машина доехала до С.

 Тогда вторая машина приехала в С через t−1 ч, а третья - через t−2 ч.

Приравняем расстояния, пройденные всеми машинами: AC=50t=60(t−1) =v(t−2), где v - скорость третьей машины в км/ч.

Из равенства 50t=60(t−1) находим t=6.

Далее находим AC=300 км.

Тогда из 60(t−1) =v(t−2) получаем, что v=75 км/ч
Ответ: за 75 км/ч

С2. Самат разместил в первый альбом 20% своих марок, во второй  остатка, а в третий – остальные 56 марок. Сколько марок всего у Самата?

Решение:

Пусть у Самата было  марок. Тогда в 1-й альбом он разместил  марок. Во второй альбом он разместил  остатка, т.е.

Найдем сколько марок разместили в третий альбом:

В третьем альбоме 56 марок, имеем:

Учащиеся отвечают на вопросы рефлексии:

-        Что сегодня я узнал?

-        Мне было тяжело или нет?

-        Я понял материал или были затруднения?

-        Я научился чему-то новому?

-        Я смог добиться результата?

Ресурсы:

1.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

2.      Алдамуратова Математика. 6 класс. Алматы. «Атамура». 2011 год.

3.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

4.       Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.