14. Решение текстовых задач Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока "Решение текстовых задач с помощью уравнений "

Цели обучения:

6.5.1.6

решать текстовые задачи с помощью составления линейных уравнений;

Критерии оценивания

Учащийся:

знает:

как решать текстовые задачи с помощью составления линейных уравнений;

умеет:

·         составлять математические модели при решении текстовых задач с помощью составления линейных уравнений;

·         решать текстовые задачи с помощью составления линейных уравнений;

·         обосновывает свое решение.

Теоретический материал:

Решая задачу, необходимо выделить три этапа математического моделирования:

1. составление математической модели;
2. работа с математической моделью;
3. ответ на вопрос задачи.

Чтобы составить математическую модель задачи необходимо выполнить

       I.      анализ задачи (расчленение задачи на условия и вопрос, выделение в условиях объектов и их характеристик);

    II.      схематическая запись задачи (наглядная форма записи результатов анализа задачи, может быть представлена в виде таблицы, схемы, рисунка, краткой записи);

 III.      запись уравнения.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа с классом. Ввод в тему урока, используя основные знания и навыки по решению текстовых задач  с помощью составления линейных уравнений.

Приложение 1

1) Раскрой скобки и приведи подобные слагаемые:

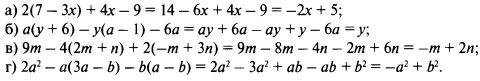
2) Найди множество корней уравнения:

3. Турист преодолел 600 км - сначала летел на самолете, а оставшуюся часть пути проехал на автобусе. Путь на самолете в 19 раз больше, чем на автобусе. Сколько километров турист проехал на автобусе?

4. В книге 200 страниц. Коля прочитал ее за 2 дня. В первый день он прочитал в 4 раза больше, чем во второй. Сколько страниц прочитал Коля во второй день?

5. От города до поселка автомобиль доехал за 3 ч. Если бы скорость была увеличена на 25 км/ч, то путь длился бы 2 ч. С какой скоростью ехал автомобиль и чему равно расстояние от города до поселка?

Пригласите к доске ученика, попросите его записать подробное решение задания. Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске, внимательно слушают одноклассников. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого задания, акцентируйте их внимание на обоснование решений. Для учащихся с более высокой скоростью решения организуйте "уголок Знайки", куда они могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задачи, а работать в это время с остальной частью класса.

При наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 2

1)Длина прямоугольника в 4 раза больше ширины. Длину прямоугольника уменьшили на 20%, а ширину увеличили на 20%. На сколько процентов изменились периметр и площадь прямоугольника?

Решение:

2) От турбазы до станции турист доехал на велосипеде за 3 ч. Пешком он мог бы пройти это расстояние за 7 ч. Известно, что скорость пешком у него на 8 км/ч меньше, чем на велосипеде. С какой скоростью ехал турист и чему равно расстояние от турбазы до станции?

Решение: Пусть скорость передвижения пешком х км/ч, тогда х+8 км/ч скорость передвижения на велосипеде. На велосипеде он передвигался 3 часа и проехал бы 3(x+8) километров. Пешком он двигался бы 7 часов, значит он мог пройти 7x километров Известно, что расстояния равны: 7x=3(x+8)

7x=3x+24;      4x=24;            x=24 : 4

x=6

6 км/ч - скорость движения пешком

6+8=14(км/ч) - скорость движения на велосипеде

6∙7=42(км) - от станции до турбазы

Ответ: 14 км/ч, 42 км.

3) В первом контейнере в 5 раз больше моркови, чем во втором. Когда из первого контейнера взяли 25 кг моркови, а во второй засыпали еще 15 кг, то в обоих контейнерах моркови стало поровну. Сколько моркови было в каждом контейнере первоначально?

Ответ: 10 кг, 5∙10=50 кг.

4) В первом мешке в 3 раза больше картофеля, чем во втором. После того как из первого мешка взяли 30 кг, а во второй насыпали еще 10 кг, в обоих мешках картофеля стало поровну. Сколько картофеля было в каждом мешке первоначально?

Ответ: 20(кг) картофеля в 1 мешке; 3∙20=60(кг) картофеля во 2 мешке.

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Работа в парах. Взаимное обучение. Создать пары из представителей разных групп обучаемости. Для закрепления материала и оценки усвоения теоретического материала предложить задания, из учебного пособия "Математика 6", аналогичные заданиям Приложения 3.

Приложение 3

1) Решить уравнение:

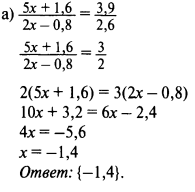
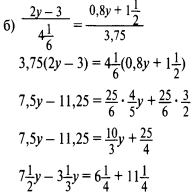
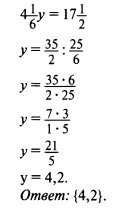
2) Найти множество корней уравнения:

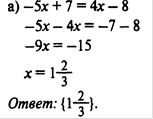
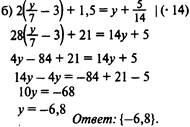
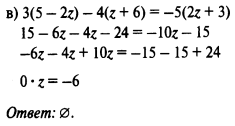
Решить задачи:

3). За 6 ч ученик токаря сделал столько деталей, сколько сам токарь за 4 ч. Известно, что токарь делает за 1 ч на 5 деталей больше, чем ученик. Сколько деталей за 1 ч изготовлял ученик?

4) За 3 дня турист прошел 90 км. Во второй день он прошел на 10 км меньше, чем в первый, а в третий - 0,8 пройденного в первые 2 дня. Какое расстояние турист проходил в каждый из трех дней?

5) В первом ящике в 2 раза больше гвоздей, чем во втором. После того как из первого ящика взяли 5 кг гвоздей, а из второго - 10 кг, в первом стало в 3 раза больше, чем во втором. Сколько гвоздей было раньше в каждом ящике?

Проверить ответы по ключам. Сравнить, проверить правильность ответов, провести анализ ошибок.

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания, аналогичные заданиям Приложения 4 из учебного пособия "Математика 6".

Приложение 4

1) В 2 сарая сложили сено, причем в первый сарай в 3 раза больше, чем во второй. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько тонн сена было в каждом сарае первоначально?

2) На одном участке было в 5 раз больше саженцев смородины, чем на втором. После того как с первого участка увезли 50 саженцев, а на втором посадили еще 90, на обоих участках кустов стало поровну. Сколько саженцев смородины было на каждом участке первоначально?

3) Сумма трех последовательных чисел равна 684. Найдите каждое из этих чисел.

Сравнить, проверить правильность ответов, провести анализ ошибок.

После окончания выполнения, попросить обменяться тетрадями с соседом. Провести взаимопроверку по ключу. Собрать информацию о выполнении. Разобрать задания вызвавшие затруднения.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.      "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.      "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.