Добавить материал

и получить 10 документов
и свидетельство автора

Рыбинок Екатерина Валерьевна

3Дидактический материал 2 Индивидуальная самостоятельная работа

docx
12.05.2020

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

3Дидактический материал 2 Индивидуальная самостоятельная работа.docx

Индивидуальная самостоятельная работа

Уровень А

1. Найдите члены арифметической прогрессии , обозначенные буквами:

Критерий оценивания	дескриптор	балл
при решении задач использует формулу характеристического свойства арифметической прогрессии;	используя формулу характеристического свойства арифметической прогрессии находит неизвестное ;	1
	используя формулу характеристического свойства арифметической прогрессии находит неизвестное ;	1
	находит разность арифметической прогрессии	1
	используя формулу характеристического свойства арифметической прогрессии находит неизвестное ;	1

Решение:

Используя характеристическое свойство арифметической прогрессии находим:

Ответ:

Уровень В

1. Даны три функции , , .

Найдите значение t , если числа в указанном порядке образуют арифметическую прогрессию. Найдите эти числа.

Критерий оценивания	дескриптор	балл
при решении задач использует формулу характеристического свойства арифметической прогрессии;	используя формулу характеристического свойства арифметической прогрессии находит неизвестное ;	1
	используя формулу характеристического свойства арифметической прогрессии находит неизвестное ;	1
	используя формулу характеристического свойства арифметической прогрессии находит неизвестное ;	1

Решение:

Используем характеристическое свойство арифметической прогрессии:

- арифметическая прогрессия, если - средний член, то.

, ,

Ответ:

Уровень С

1. Числа удовлетворяют следующим условиям::.

Докажите, что числа в указанном порядке образуют арифметическую прогрессию.

Критерий оценивания	дескриптор	балл
при решении задач использует формулу характеристического свойства арифметической прогрессии;	используя формулу характеристического свойства арифметической прогрессии выражает ;	1
	использует свойство пропорции	1
	преобразует выражение	1
	выполняет тождественное преобразование	1

Решение:

Используем характеристическое свойство арифметической прогрессии:

Если выполняется это условие, то три числа образуют арифметическую прогрессию:

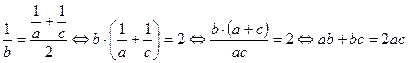
Отсюда следует, что числа образуют арифметическую прогрессию.

Уровень С 1. Числа удовлетворяют следующим условиям : :

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также