49 Переместительное и Методические рекомендации к уроку. Вариант 2

Методические рекомендации к уроку

Тема урока "Переместительное и сочетательное свойства умножения рациональных чисел"

Цели обучения:

6.1.2.17

применять свойства сложения и умножения рациональных чисел

Критерии оценивания

Учащийся:

знает:

cвойства умножения;

умеет:

использовать переместительное, сочетательное,  распределительное свойства умножения и применяет их при вычислениях.

Теоретический материал:

Свойства сложения и умножения

Операции сложения и умножения рациональных (а значит, в том числе и натуральных, и целых) чисел обладают следующими свойствами:

·         ab = ba (переместительный закон умножения).

·         (ab)c = a(bc) (сочетательный закон умножения).

Переместительный закон также называется также коммутативным. Его смысл в том, что результат не меняется при перестановке сомножителей.

Сочетательные законы также называют ассоциативными. Их смысл в том, что результат не меняется при группировке сомножителей.

Сочетательный (ассоциативный) закон умножения : ( a · b ) · c = a · ( b · c ) = a · b · c . Произведение не зависит от группировки его сомножителей.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Выполнить действия (устно):

Совместно с учащимися определить тему и цели урока, зону ближайшего развития.

Работа с классом. Провести ввод новой темы, основываясь на знания и опыт работы учащихся с целыми числами. Цель: Основываясь на знания учащихся законов умножения для ранее изученных множества чисел и опыт использования для рациональных вычислений, введем и для чисел отрицательных, положительных и чисел с разными знаками переместительное и сочетательное свойства умножения рациональных чисел.

Переместительное свойство умножения:

От перестановки сомножителей местами произведение не меняется.

Следовательно, для любых чисел a и b верно равенство: a · b = b · a выражающее переместительное свойство умножения.

Примеры:

6 · 7 = 7 · 6 = 42;       4 · 2 · 3 = 3 · 2 · 4 = 24

Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.

Переместительное свойство умножения позволяет выбирать более удобный способ умножения чисел.

Применение переместительного свойства умножения позволяет облегчить вычисления.

Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.

Следовательно, для любых чисел a, b и c верно равенство:

a · b · c = (a · b) ·c = a · (b ·c), выражающее сочетательное свойство умножения.

Пример:

(-2) · 3  · 5 = -3 · (2 · 5) = 3 · 10 = 30

или     3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30

Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:

-25 · 15 · (-4) = (25 · 4) · 15 = 100 · 15 = 1500

В данном случае можно было вычислить всё последовательно:

25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500

но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.

Для закрепления, при наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Групповая работа.

Объединить учащихся в разноуровневые группы по 4 - 6 учеников. Раздать каждой группе карточки с заданиями.

Приложение 1

1) Сформулируйте словами сочетательное свойство умножения а(bс) = (ab)c и проверьте его:

2) применяя переместительное и сочетательное свойства умножения рациональных чисел, найдите значение выражения:

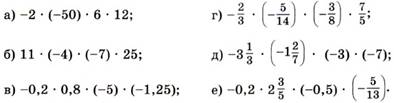
3) Какое получится число (положительное или отрицательное), если перемножить:

а) одно отрицательное и два положительных числа;

б) два отрицательных и одно положительное число;

в) 7 отрицательных и несколько положительных чисел;

г) 20 отрицательных и несколько положительных?

Сделайте вывод.

Учитель проходит по рядам, слушает, при необходимости корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям

Каждая группа демонстрирует свой результат выполнения задания..

Старший группы оценивает вклад каждого, выставляя отметку.

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить тест. Каждый выполняет самостоятельно.

Приложение 2

1.      Значение выражения  равно:

А. 1,8.             В. -0,18.                      С. 0,18.                       D. -0,018.                   Е. 0,018.

2.      Значение выражения  равно:

А. -0,3.           В. 3.                С. 0,3.             D. -3.               Е. 0,03.

3.      Значение выражения  равно:

А. .         В. .         С. .         D. .         Е. .

4.      Значение выражения  равно:

А. -30.            В. -32.             С. -29.             D. -43.             Е. -20.

5.      Значение выражения 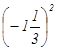 равно:

А. .            В. .         С. .         D. .            Е. .

6.      Значение выражения  равно:

А. .          В. .       С. .       D. .       Е. .

7.      Значение выражения  равно:

А. .      В. .                  С. .      D. .         Е. .

8.      Значение выражения  равно:

А. -0,025.                   В. 0,025.         С. 0,0225.                   D. 2,25.           Е. -0,225.

9.      Значение выражения  равно:

А. 5,12.           В. -0,512.        С. -5,12.          D. -0,0512.      Е. 0,512.

10.  Значение выражения  равно:

А. 0,000216.               В. 0,216.         С. 0,0216.                   D. 0,00216.     Е. 0,0000216.

11.  Значение выражения  равно:

А. .              В. .         С. .            D. .          Е. .

После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать один из вариантов.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных группах (разного уровня обучаемости). Ученики, распределяя в группе задания, самостоятельно выбирают уровень сложности.

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания на нахождение произведения, используя законы умножения.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Математика. 6 класс Виленкин Н. Я.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В. 

Интернет ресурсы:

http://www.yaklass.ru

https://school-assistant.ru