Teacher Guides of the Lesson

Theoretical material for the lesson, definitions for concepts 

Figure 1

A bubble chamber image of the tracks of subatomic

particles. The tracks curve because the charged

particles are affected by the presence of a magnetic field.

 

Moving Moving particles

              The world of atomic physics is populated by a great variety of particles – electrons, protons, neutrons, positrons and many more. Many of these particles are electrically charged, and so their motion is influenced by electric and magnetic fields. Indeed, we use this fact to help us to distinguish one particle from another. Figure shows the tracks of particles in a detector called a bubble chamber. A photon (no track) has entered from the top and collided with a proton; the resulting spray of nine particles shows up as the gently curving tracks moving downwards. The tracks curve because the particles are charged and are moving in a magnetic field. The tightly wound spiral tracks are produced by electrons which, because their mass is small, are more dramatically affected by the field. In this chapter, we will look at how charged particles behave in electric and magnetic fields and how this knowledge can be used to control beams of charged particles. At the end of the chapter, we will look at how this knowledge was used to discover the electron and to measure its charge and mass.

An electron beam tube (Figure 2) can be used to demonstrate the magnetic force on a moving charge. A beam of electrons is produced by an ‘electron gun’, and magnets or electromagnets are used to apply a magnetic field.

You can use such an arrangement to observe the effect of changing the strength and direction of the magnetic field, and the effect of reversing the field. If you are able to observe a beam of electrons like this, you should find that the force on the electrons moving through the magnetic field can be predicted using Fleming’s left-hand rule. In Figure 3, a beam of electrons is moving from right to left, into a region where a magnetic field is directed into the plane of the paper. Since electrons are negatively charged, they represent a conventional current from left to right. Fleming’s left hand rule predicts that, as the electrons enter the field, the force on them will be upwards and so the beam will be deflected up the page. As the direction of the beam changes, so does the direction of the force. The force due to the magnetic field is always at 90° to the velocity of the electrons. It is this force that gives rise to the motor effect. The electrons in a wire experience a force when they flow across a magnetic field, and they transfer the force to the wire itself. In the past, most oscilloscopes, monitors and television sets made use of beams of electrons. The beams were moved about using magnetic and electric fields, and the result was a rapidly changing image on the screen.

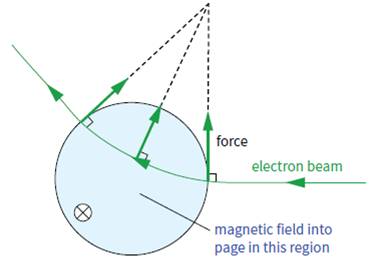
Figure 4

The magnetic force on a moving charge

We can make an intelligent guess about the factors that determine the size of the force on a moving charge in a uniform magnetic field (Figure 4). It will depend on:

■■ the magnetic flux density B (strength of the magnetic field)

■■ the charge Q on the particle

■■ the speed v of the particle.

The magnetic force F on a moving particle at right angles to a magnetic field is given by the equation:

F = BQv

The direction of the force can be determined from Fleming’s left-hand rule. The force F is always at 90° to the velocity of the particle. Consequently, the path described by the particle will be an arc of a circle.

Figure 5

If the charged particle is moving at an angle θ to the magnetic field, the component of its velocity at right angles to B is v sin θ. Hence the equation becomes:

F = BQv sin θ

We can show that the two equations F = BIL and F = BQv are consistent with one another, as follows.

Since current I is the rate of flow of charge, we can write: I = Qt

Substituting in F = BIL gives:                  F = BQL

t

Now, Lt is the speed ν of the moving particle, so we can write:

F = BQv

For an electron, with a charge of −e, the magnitude of the

force on it is:

F = Bev (e = 1.6010⁻¹⁹ C)

The force on a moving charge is sometimes called ‘the Bev force’; it is this force acting on all the electrons in a wire which gives rise to ‘the BIL force’. Here is an important reminder: The force F is always at right angles to the particle’s velocity v, and its direction can be found using the left-hand rule (Figure 5).

 

 

Instructions for demonstrations and safety

Warning: experiments with electricity should be performed under the supervision of teachers or adults familiar with electricity safety procedures.

 

Additional guidelines for organizing a lesson 

1.      Organization moment. Establishing emotional state. Checking for absent students.

2.      Teacher shows a picture on presentation and asks students: Why the electron beam is deflected as it passes through charged metal plates?

3.      Individual students were called on to respond to questions and share their own opinions/thoughts. Then she explains that the tracks curve because the charged

particles are affected by the presence of a magnetic field.

4.      Teacher introduces the topic and objectives of the lesson, assess criteria.

5.      If a fine beam electron tube is not available,  teacher just uses  a picture of electron beam tube and describes the effects of magnetic fields on moving charges .

6.      Teacher leads learners to derivation of the formula F = BQv sin θ. Use the Fleming’s Left Hand Rule to find the direction of Lorentz force.

7.      Teacher asks learners to take cards (one side is empty, another side has a name of a group) and to divide into two/three groups. They answer questions step by step in groups.

Teacher check and assess students ability to use Fleming’s left hand rule to determine the velocity of a charge, the direction of the magnetic field, and the direction of the magnetic force on a moving charge. Assessment criteria and score for each round should be agreed in advance.

8.      At the end of the lesson students are encouraged to reflect on what they have learned and

what they need to improve.

 

Recommendations for formative assessment

 

Activity 1. Students discuss learning objectives and assess criteria.

         Activity 2. Individual students were called on to respond to the teacher question related to the

                       picture and share their own opinions/thoughts.

           Activity 3. Learners derive the formula by Teacher's Support F = BQv sin θ. Use the Fleming’s 

                           Left Hand  Rule to find the direction of Lorentz force.

         Activity 4. Learners take cards (one side is empty, another side has a name of a group) and

                           divided into two/three groups. They answer questions step by step in groups. They are

                          checked and assessed by a teacher for ability to use Fleming’s left hand rule to

                          determine the velocity of a charge, the direction of the magnetic field, and the

                           direction of the magnetic force on a moving charge.

 

Activity 5. At the end of the lesson students are encouraged to reflect on what they have learned

                and what they need to improve.

 

 

Answers, criteria for assignments, additional materials for the lesson

Activity 4.

Ø  I Round – Multiple choice Question [2]

Ø  II Round – Test Yourself                   [2]

Ø  III Round – Problem solving             [3]

 

Multiple choice question (2 score)

1. A charged particle is situated in a region of space and it experiences a force only when it is in motion. Which of the following states the field or fields enclosed in the region correctly?

A) An electric field only

B) Both a magnetic field and an electric field

C) Both an electric field and a gravitational field

D) Both a magnetic field and a gravitational field

E) A magnetic field only

Answer

E                                                                                                                                                      [1]

Explanation: Magnetic fields exert forces on charged particles only if those particles are moving.      

                                                                                                                                                         [1]

 

Test Yourself (2 score)

2. Refer to the following information for the next two questions.

 

 

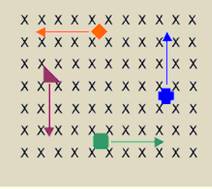
If the orange diamond particle shown above is negatively charged, in which direction is the magnetic force acting on it while it is at the position shown?

A)      Towards the right side of the page (+x)

B)      Towards the left side of the page (-x)

C)      Towards the top of the page (+y)

D)      Towards the bottom of the page (-y)

E)        None of the above

 

 

Answer C                                                                                                                                   [1]

True or False? As the magnetic force acts on the particles shown in the diagram above, it does work on each one. This would be evidenced by a change in the kinetic energy of each particle.

 

Answer: False                                                                                                                             [1]

 

 

3. What is the direction of the magnetic field that produces the magnetic force on a positive charge as shown in each of the three cases in the figure below, assuming  is perpendicular to ?

 

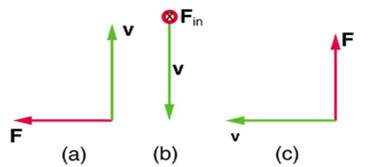
Answer

(a) Into page                                                                                                                                  [1]

(b) West (left)                                                                                                                               [1]

(c) Out of page                                                                                                                              [1]

 

 

Solving problem (3 score)

 

4. A cosmic ray proton moving toward the Earth at  5.0 ∙ 10⁷ m/s experiences a magnetic force of  1.70 ∙ 10^-16 N. What is the strength of the magnetic field if there is a  45⁰  angle between it and the proton’s velocity?

•      B = F / qv                                                                                                                          [1]

•      B = 1.70 ∙ 10^-16 N / 1.6 ∙ 10^-19 C × 5.0 ∙ 10⁷ m/s                                                                 [1]

•      B = 3.0 ∙ 10^-5 T                                                                                                                   [1]

 

List of useful links and literature 

Douglas C. Giancoli, Physics Principles with Applications, Seventh edition  2014.

David Sang, Graham Jones, Gurinder Chadha and Richard Woodside, Cambridge International    

AS and A Level Physics Coursebook Second Edition, 2014

https://tap.iop.org/fields/electromagnetism/413/page_46935.html

 https://opentextbc.ca/physicstestbook2/chapter/magnetic-field-strength-force-on-a-moving-    

charge-in-a-magnetic-field/#fs-id1327231

 http://www.schoolphysics.co.uk/age14- 

16/Atomic%20physics/text/Cathode_ray_deflection_tube/index.html

 

Скачано с www.znanio.ru